План урока: Вводное слово учителя с показом рисунков. Рассказ учителя об истории развития геометрии
| Вид материала | План урока |
- План урока Вводное слово учителя. Целеполагание, 117.05kb.
- План урока Опережающее домашнее задание Вводное слово учителя Запись на доске, 40.64kb.
- План-конспект урока биологии в 11 классе по теме: Взгляды, гипотезы, 192.07kb.
- Задачи урока Основные понятия тсо оборудование Вводное слово учителя Вопрос учащимся, 109.28kb.
- План урока: Повторение изученного ранее (географический диктант) Изучение нового материала., 73.84kb.
- План урока: Вступительное слово учителя. Доклады учащихся, 42.28kb.
- Психологический портрет человека, 12.74kb.
- Программа кружка по астрономии «Физика космоса», 30.16kb.
- Конспект урока по биологии 6 класс Игра «О! Счастливчик!», 87.37kb.
- План урока: Вступительное слово учителя-ведущего. Приветствие команд, представление, 33.66kb.
Вводный урок геометрии в 7-м классе "Краткая история возникновения и развития геометрии. Геометрические фигуры. Точка и прямая.
Цели и задачи.
Образовательные – познакомить учащихся с историей возникновения геометрии, с первыми основными геометрическими понятиями: точка и прямая, «лежать между» («лежать на») для точек прямой, с их условными обозначениями; с простейшими геометрическими фигурами на плоскости.
Развивающие – развивать творческую и мыслительную деятельность учащихся на уроке с помощью решения задач исследовательского характера, интеллектуальные качества личности школьников такие, как самостоятельность, способность к оценочным действиям, обобщению, быстрому переключению; способствовать формированию навыков самостоятельной работы; формировать умение четко и ясно излагать свои мысли.
Воспитательные – прививать учащимся интерес к предмету с помощью изучения истории и развития науки, применения информационных технологий (с использованием компьютера); формировать умение аккуратно и грамотно выполнять математические записи.
План урока:
- Вводное слово учителя с показом рисунков.
- Рассказ учителя об истории развития геометрии.
- Выделение основных понятий планиметрии.
- Повторение ранее изученного геометрического материала, математических символов и выполнение учащимися задания на взаимное расположение точек и прямых на плоскости.
- ДИКТАНТ.
- Проверка усвоения изученного материала в форме кроссворда.
- Подведение итогов урока. Выставление оценок. Домашнее задание.
Ход урока
- Вводное слово.
ЛЮДИ ИЗДАВНА ИНТЕРЕСУЮТСЯ ОКРУЖАЮЩИМ МИРОМ И ДЛЯ ИЗУЧЕНИЯ ЕГО СОЗДАЛИ РАЗЛИЧНЫЕ НАУКИ. в КАЖДОЙ ИЗ НАУК ИЗУЧАЮТСЯ ПРЕДМЕТЫ И ЯВЛЕНИЯ С КАКОЙ-НИБК\УДЬ ТОЧКИ ЗРЕНИЯ. ПРИ ЭТОМ ОНИ НЕ ОБРАЩАЮТ ВНИМАНИЯ НА НЕКОТОРЫЕ СВОЙСТВА ИЗУЧАЕМЫХ ОБЪЕКТОВ, КОТОРЫЕ НЕ СУЩЕСТВЕННЫ ДЛЯ ДАННОЙ НАУКИ.
ПРИХОДИЛОСЬ ЛИ ВАМ СЛЫШАТЬ КОГДА-НИБУДЬ СЛОВО «ГЕОМЕТРИЯ»? ЗНАЕТЕ ЛИ ВЫ, ЧТО ОНА ОЗНАЧАЕТ, ЧТО ИЗУЧАЕТ?
Вопросы:
Что означает слово «геометрия»?
Когда, как и с какой целью зародилась наука – геометрия?
Кого можно считать основоположниками геометрии? Как называлось первое дошедшее до нас научное изложение геометрии?
Какие можно выделить этапы развития геометрии?
Что изучает геометрия?
Как можно объяснить, что такое точка, прямая, отрезок?
Начиная с 7-го класса вы будете изучать новый предмет, который называется геометрия. Работа на уроке позволит ответить на поставленные вопросы.
Слово «Геометрия»-греческое слово .Разберем слово «геометрия» по частям :гео-метрия. Какие еще слова начинаются со слова «гео»? (география, геодезия, геофизика). Геология-наука о строении, минеральном составе, закономерностях истории земли, геодезия- наука о форме и размерах земли, география-наука мо земной поверхности, населения и его деятельности. Следовательно «гео» означает земля, а что означает «метрия». Вспомним, для чего нужен метр и где поль зуемся метром (для измерения). Следовательно, слово «геометрия» переводится как землемерие.
2. История возникновения геометрии.
Великий немецкий математик Вильгельм Лейбниц сказал: «Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет».
Заглянем в прошлое, когда зародилась наука геометрия....
Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова, вкусные орехи от горьких и т.д. Особенно вкусными казались им орехи кокосовой пальмы, которые имеют форму шара. А добывая каменную соль, люди наталкивались на кристаллы, имевшие форму куба. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими формами.
Уже 200 тысяч лет тому назад были изготовлены орудия сравнительно правильной геометрической формы, а потом люди научились шлифовать их. Специальных названий для геометрических фигур, конечно, не было. Говорили: «такой же, как кокосовый орех» или «такой же, как соль» и т.д.
А когда люди стали строить дома из дерева, пришлось глубже разобраться в том, какую форму следует придавать стенам и крыше, какой формы должны быть бревна. Сами того не зная, люди все время занимались геометрией: женщины, изготавливая одежду, охотники, изготавливая наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.
Когда стали строить здания из камня, пришлось перетаскивать тяжелые каменные глыбы. Для этого применялись катки. И заметили, что перекатка проще, если взять кусок дерева с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одним из важнейших тел – цилиндром. Скалками цилиндрической формы пользовались и женщины, раскатывая белье после стирки.
Перевозить грузы на катках было довольно тяжело, потому что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластинки и с их помощью перетаскивать грузы. Так появилось первое колесо.
Но не только в процессе работы знакомились люди с геометрическим фигурами.
Издавна они любили украшать себя, свою одежду, свое жилище (бусинки, браслеты, кольца, украшения из драгоценных камней и металлов, роспись дворцов).
Для того, чтобы взимать налоги с земли, необходимо было знать их площадь. Гончару необходимо было знать, какую форму следует придать сосуду, чтобы в него входило то или иное количество жидкости. Астрономы, наблюдавшие за небом и дававшие на основе этих наблюдений указания, когда начинать полевые работы, должны были научиться определять положение звезд на небе. Для этого понадобилось измерять углы.
Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т.д.
Древние египтяне были замечательными инженерами. До сих пор не могут до конца разгадать загадки огромных гробниц Египетских царей – Фараонов.
Пирамиды – а они построены более 5 тыс. лет назад – состоят из каменных блоков весом 15 тонн, и эти «кирпичики» так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы – рычаги и катки.
« Все боится времени, но само время боится пирамид».
В Вавилоне при раскопках ученые обнаружили остатки каменных стен, высотой в несколько десятков метров, а высота Вавилонской башни достигает 82 метра.
Без математических знаний все эти сооружения невозможно было бы построить. И все же математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой, поэтому правила надо было зазубривать, не понимая, почему надо применять то, а не другое.
Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз древней школы был: "Не знающие геометрии не допускаются!"
(Пифагор VI век до н.э., основал свою школу)
Настает время привести все разрозненные знания в систему.
И наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э.) в своих книгах «Начала». Произведение состояло из 13 томов, описанная в этих книгах геометрия получила название Евклидова.
Конечно, геометрия не может быть создана одним ученым. В работе Евклид опирался на труды десятков предшественников и дополнил работу своими открытиями и изысканиями. Сотни раз книги были переписаны от руки, а когда изобрели книгопечатание, то она много раз переиздавалась на языках всех народов и стала одной из самых распространенных книг в мире.
В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более короткого пути для понимания геометрии, чем тот, который описан в его знаменитом труде, содержащемся в 13 книгах.
Ученый гордо ответил: " В геометрии нет царской дороги".
В течение многих веков «Начала» были единственной учебной книгой, по которым молодежь изучала геометрию. Были и другие. Но лучшими признавались «Начала» Евклида. И даже сейчас, в наше время, учебники написаны под большим влиянием «Начал» Евклида.
Несмотря на то, что содержание геометрии расширилось далеко за пределы учения о земле, она по-прежнему продолжает называться «Геометрией».
3.Богатую коллекцию геометрических тел дают нам геологические и биологические объекты. Например, плоды различных растений чрезвычайно разнообразны как по вкусу и аромату. Так по форме и размерам. Смородина, клюква, апельсин, арбуз обладают совершенно разными вкусами и значительно различаются по размеру, но с точки зрения геометрии их объединяет то, что о ни обладают формой шара. Поэтому несъедобный одуванчик, имеющий ту же форму, с точки зрения геометрии ничем не отличается от арбуза, апельсина, клюквы. (На доску прикреплены цветные рисунки апельсина, клюквы, арбуза и одуванчика).
В жизни встречаются множество предметов, сгруппированные по какому-то определенному принципу.
Посмотрите на эти рисунки (Водном ряду рисунки дерева, пушки, башни. В другом- горы, грибы, шишки. В 3-ем ряду- шкаф, спичечный коробок, кирпич, многоэтажный дом).
1. Определите по какому принципу они объединены? Что вам сразу бросилось в глаза (Все они имеют одну форму).
2. Ответьте, какую именно форму?
Итак. Мы рассмотрели самые разные предметы и объекты. Не будем обращать внимание на то, какого они цвета, из чего они сделаны и т.д. Ведь в каждом из них есть то, что объединяет его со многими другими предметами и объектами. Это-форма. Все рассмотренные объекты и предметы каждой группы имеют одинаковую форму. И ствол дерева, и ствол пушки, и башня имеют цилиндрическую форму. Шишки, шляпы грибов, горы- коническую форму. Шкаф, спичечный коробок, кирпич, многоэтажный дом- прямоугольный параллелепипед. Таким образом, геометрическая фигура (тело)-это абстрактный предмет, в котором рассматриваются только форма и размер, не обращая на физические свойства.
4. Фронтальная работа.
Чтобы представить себе геометрическую фигуру, нужно внимательно посмотреть на окружающие нас предметы и объекты. Найдите в классе геометрические объекты, похожие на объекты 1-3 групп.
Цилиндр. Кто-нибудь знает, почему эту фигуру называют цилиндром? Посмотрите на цилиндр и начертите его. Очень- очень давно, когда не было техники, люди, чтобы перетащить тяжелый груз с одного места на другое, использовали катки. Для этого они подыскивали прямое дерево и отрезали от него часть, везде примерно одинаковую по толщине. Слово «цилиндр» означает на греческом языке «каток, валик». У цилиндра два основания. Беру конус. Конус переводится с греческого как шишка или верхушка шлема.
5. Расположение геометрических фигур рассматривают различные разделы геометрии.
Практическая работа.
Теперь возьмите треугольник, четырехугольник, разместите их в плоскости тетради. А теперь попробуйте разместит цилиндр в плоскости тетради.
Вывод: Итак, человека окружают плоские и пространственные тела.. Геометрические фигуры, точки которых лежат в одной плоскости. Изучает планиметрия. Геометрические фигуры, точки которых не лежат в одной плоскости изучает стереометрия.
Геометрия-наука о свойствах геометрических фигур.
Планиметрия Стереометрия.
Мы начинаем изучать геометрию с плоских фигур.
6. Знакомство с геометрическими инструментами.
На уроках геометрии вы научитесь представлять и сравнивать геометрические фигуры и тела, учитесь рассуждать, ставить вопросы, анализировать, будете чертить, рисовать ,конструировать. А для этого нужны различные инструменты, какие именно- узнаете, отгадав загадки.
Палочка волшебная
Есть у мен, друзья.
Палочкою этой
Могу построить я
Башню, дом и самолет
И большущий пароход. (карандаш)
В тетради я бываю
Косая и прямая.
В другом совсем значении
Я планка для черчения.
И ,наконец, порою
В шеренгу я построю. (линейка)
Сговорились две дуги
Делать дуги и круги.(циркуль)
Два конца, два кольца
Посередине гвоздик. (ножницы)
Даже самое большое здание складывается из маленьких кирпичей, так и сложные геометрические фигуры составляются из простейших фигур.
В геометрии выделяют основные фигуры, одну из них узнаете, ответив на вопросы.
Доктор сделал мне укол,
Братик капнул клей на пол.
Мишку, моего соседа,
Укусить оса успела.
Так на фоне пустоты
Все оставили следы.
-Что же это будет, дети?
_Точка!-
Конечно, геометрия дает не только представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, то есть логически мыслить.
Мы начинаем изучать планиметрию.
Как вы думаете, какие самые основные понятия планиметрии?
Даже самое большое здание складывается из маленьких кирпичей, так и сложные геометрические фигуры составляются из простейших фигур.
Конечно, самая главная - это точка.
Почти все названия геометрических фигур греческого происхождения, как и само слово геометрия. Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский язык.
Точка – результат мгновенного касания, укол
Отсюда же произошел медицинский термин пункция-прокол.
Пунктир.
Линия – льняная нить.
Линолеум – первоначально означал промасленное льняное полотно.
Как уже было сказано ранее, все названия геометрических фигур первоначально были названиями конкретных предметов, имеющих форму, более или менее близкую к форме данной фигуры.
4. Повторение известного материала о точках и прямых и их расположении относительно друг друга.
Давайте вспомним, как обозначают на чертеже прямые и точки.
- Прямая безгранична, поэтому на чертеже изображают часть.
- Прямые обозначают двумя заглавными латинскими буквами, соответствующим двум точкам на прямой или одной малой буквой.
- Точки обозначают заглавными латинскими буквами.
- Знак
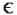означает принадлежит, т.е. А1 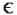m означает, что точка А1 принадлежит прямой m или лежит на ней. И А2
m соответственно, не принадлежит или не лежит.Выполнить задание
Опишите этот рисунок. Запишите рассказ, используя условные обозначения.
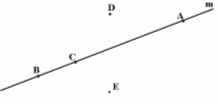
9. Диктант.
1.Проведите прямую, обозначьте ее двумя способами.
2.Прведите прямую а, отметьте точку С, которая лежит на прямой а, точку Д, которая не лежит на прямой а. Проведите прямую в, проходящую через точку Д и пересекающую прямую а. Обозначьте точку пересечения прямых буквой Е.
Самопроверка диктанта, выставление оценок.
10. Проверка усвоения изученного материала.
Учитель выдает кроссворд каждому ученику.
Кроссворд
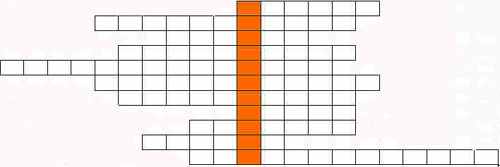
- Вставь пропущенное слово: «Через любые две точки можно провести ... ; и при том только одну».
- Математический знак
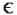
- Название книги, в которой впервые был систематизирован геометрический материал.
- Геометрическая фигура на плоскости.
- Геометрическая фигура в пространстве.
- Раздел геометрии.
- Математический знак
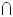
- Первоначальное понятие в геометрии.
- Часть прямой, ограниченная двумя точками.
- Древнегреческий математик.
- Геометрическая фигура на плоскости. ( номера идут сверху вниз построчно)
Если кроссворд учащиеся не успевают выполнить весь, то он выдается на дом для доработки, и следующий урок начинается с опрашивания по вопросам кроссворда. Или: тот, кто успел ответить на все вопросы кроссворда вовремя, считается полностью усвоившим урок.
Итак, что же получилось в выделенной части?
Что такое планиметрия?
11. Подведение итогов урока.
На все ли вопросы вы получили сегодня ответы? (Учитель обращает внимание учащихся на вопросы, поставленные в начале урока, и просит кратко еще раз на них ответить.)
Выставление оценок за тест.
Домашнее задание: стр. 3-6, № 1,2 на стр.7
Использованная литература:
!.А.В.Погорелов. Геометрия 9. Москва. Просвещение. 2006.
2.С.Б.Веселовский. В. Д. Рябчинская. Дидактические материалы по геометрии для 7 класса. Москва. Просвещение. 2006.
3.Б.Г.Зив. В. М .Мейлер, А. Г .Баханский. Задачи по геометрии для 7-11 классов. Москва. Просвещение. 2003.