–Ъ–Њ–љ—Б–њ–µ–Ї—В –ї–µ–Ї—Ж—Ц–є –Ј –і–Є—Б—Ж–Є–њ–ї—Ц–љ–Є ¬Ђ–Я—А–Њ—Ж–µ—Б–Є —Г –і—Ц–µ–ї–µ–Ї—В—А–Є–Ї–∞—Е¬ї –і–ї—П —Б—В—Г–і–µ–љ—В—Ц–≤ –Ј –љ–∞–њ—А—П–Љ–Ї—Г –њ—Ц–і–≥–Њ—В–Њ–≤–Ї–Є 050701 ¬Ђ–Х–ї–µ–Ї—В—А–Њ—В–µ—Е–љ—Ц–Ї–∞ —В–∞ –µ–ї–µ–Ї—В—А–Њ—В–µ—Е–љ–Њ–ї–Њ–≥—Ц—Ч¬ї
| –Т–Є–і –Љ–∞—В–µ—А–Є–∞–ї–∞ | –Ъ–Њ–љ—Б–њ–µ–Ї—В |
- –Ъ–Њ–љ—Б–њ–µ–Ї—В –ї–µ–Ї—Ж—Ц–є –Ј –і–Є—Б—Ж–Є–њ–ї—Ц–љ–Є ¬Ђ–Х–ї–µ–Ї—В—А–Њ—В–µ—Е–љ—Ц—З–љ—Ц –Љ–∞—В–µ—А—Ц–∞–ї–Є¬ї –і–ї—П —Б—В—Г–і–µ–љ—В—Ц–≤ –Ј –љ–∞–њ—А—П–Љ–Ї—Г –њ—Ц–і–≥–Њ—В–Њ–≤–Ї–Є, 653.08kb.
- –†–Њ–±–Њ—З–∞ –љ–∞–≤—З–∞–ї—М–љ–∞ –њ—А–Њ–≥—А–∞–Љ–∞ –Ј –і–Є—Б—Ж–Є–њ–ї—Ц–љ–Є " –Х–ї–µ–Ї—В—А–Њ–њ–Њ—Б—В–∞—З–∞–љ–љ—П " –і–ї—П —Б—В—Г–і–µ–љ—В—Ц–≤ –љ–∞–њ—А—П–Љ—Г, 511.24kb.
- –Ъ—Г–ї—М–Ї–Њ –Ґ–µ—В—П–љ–∞ –Т–Њ–ї–Њ–і–Є–Љ–Є—А—Ц–≤–љ–∞, –∞—Б–Є—Б—В–µ–љ—В –Ї–∞—Д–µ–і—А–Є, 229.49kb.
- –Ю. –Т. –•–∞—А–Є—В–Њ–љ–Њ–≤ –Ї–Њ–љ—Б–њ–µ–Ї—В –ї–µ–Ї—Ж—Ц–є –Ј –і–Є—Б—Ж–Є–њ–ї—Ц–љ–Є "–Ј–µ–Љ–µ–ї—М–љ–µ –њ—А–∞–≤–Њ —Г–Ї—А–∞—Ч–љ–Є" (–і–ї—П —Б—В—Г–і–µ–љ—В—Ц–≤, 1807.04kb.
- –Т. –Ю. –Ъ–Њ–і—Ц–љ –Ї–Њ–љ—Б–њ–µ–Ї—В –ї–µ–Ї—Ж—Ц–є –Ј –і–Є—Б—Ж–Є–њ–ї—Ц–љ–Є ¬Ђ–Ю—Б–љ–Њ–≤–Є —А–µ–Ї–Њ–љ—Б—В—А—Г–Ї—Ж—Ц—Ч —Ц—Б—В–Њ—А–Є—З–љ–Є—Е –Љ—Ц—Б—В¬ї –і–ї—П, 703.58kb.
- –Э–∞–≤—З–∞–ї—М–љ–∞ –њ—А–Њ–≥—А–∞–Љ–∞ –і–Є—Б—Ж–Є–њ–ї—Ц–љ–Є "–µ–ї–µ–Ї—В—А–Њ—В–µ—Е–љ—Ц–Ї–∞" –і–ї—П –љ–∞–њ—А—П–Љ—Г –њ—Ц–і–≥–Њ—В–Њ–≤–Ї–Є: 051001 ¬Ђ–Ь–µ—В—А–Њ–ї–Њ–≥—Ц—П, 284.54kb.
- –Ъ–Њ–љ—Б–њ–µ–Ї—В –ї–µ–Ї—Ж—Ц–є –Ј –і–Є—Б—Ж–Є–њ–ї—Ц–љ–Є вАЮ –Ґ–µ—Е–љ–Њ–ї–Њ–≥—Ц—П —В—Г—А–Є—Б—В—Б—М–Ї–Њ—Ч –і—Ц—П–ї—М–љ–Њ—Б—В—Ц" –і–ї—П —Б—В—Г–і–µ–љ—В—Ц–≤ 2 –Ї—Г—А—Б—Г, 2193.28kb.
- –Ъ–Њ–љ—Б–њ–µ–Ї—В –ї–µ–Ї—Ж—Ц–є –•–Љ–µ–ї—М–љ–Є—Ж—М–Ї–Є–є, 2005 –°–љ–Њ–Ј–Є–Ї –Ю. –Т. –С–µ–Ј–њ–µ–Ї–∞ –ґ–Є—В—В—Ф–і—Ц—П–ї—М–љ–Њ—Б—В—Ц, 909.72kb.
- –Ъ–Њ–љ—Б–њ–µ–Ї—В –ї–µ–Ї—Ж—Ц–є –Ј –і–Є—Б—Ж–Є–њ–ї—Ц–љ–Є ¬Ђ—В–µ–њ–ї–Њ–µ–љ–µ—А–≥–µ—В–Є–Ї–∞¬ї –і–ї—П —Б—В—Г–і–µ–љ—В—Ц–≤ –Ј–∞ —Д–∞—Е–Њ–Љ –Љ—З, –Љ—Б, –ї–≤, –Њ–Љ—В, 290.65kb.
- –Ъ–Њ–љ—Б–њ–µ–Ї—В –ї–µ–Ї—Ж—Ц–є –Ј –і–Є—Б—Ж–Є–њ–ї—Ц–љ–Є вАЮ–†–∞–і—Ц–Њ–µ–Ї–Њ–ї–Њ–≥—Ц—П –і–ї—П —Б—В—Г–і–µ–љ—В—Ц–≤ —Б–њ–µ—Ж—Ц–∞–ї—М–љ–Њ—Б—В—Ц 040106¬† вАЮ–Х–Ї–Њ–ї–Њ–≥—Ц—П,, 1393.76kb.
5.2. –Ґ–µ–Њ—А–µ—В–Є—З–љ—Ц –≤—Ц–і–Њ–Љ–Њ—Б—В—Ц –њ—А–Њ –µ–ї–µ–Ї—В—А–Є—З–љ–µ –њ–Њ–ї–µ.
–Х–ї–µ–Ї—В—А–Њ—Б—В–∞—В–Є—З–љ–µ –њ–Њ–ї–µ вАУ –Њ–Ї—А–µ–Љ–Є–є –≤–Є–њ–∞–і–Њ–Ї –µ–ї–µ–Ї—В—А–Њ–Љ–∞–≥–љ—Ц—В–љ–Њ–≥–Њ –њ–Њ–ї—П, —Б—В–≤–Њ—А—О–≤–∞–љ–Њ–≥–Њ —Б—Г–Ї—Г–њ–љ—Ц—Б—В—О –љ–µ—А—Г—Е–ї–Є–≤–Є—Е —Г –њ—А–Њ—Б—В–Њ—А—Ц –µ–ї–µ–Ї—В—А–Є—З–љ–Є—Е –Ј–∞—А—П–і—Ц–≤, —П–Ї—Ц —В–∞–Ї–Њ–ґ –љ–µ–Ј–Љ—Ц–љ–љ—Ц –≤ —З–∞—Б—Ц. –Ь—Ц–љ–ї–Є–≤–µ –µ–ї–µ–Ї—В—А–Є—З–љ–µ –њ–Њ–ї–µ –љ–µ–Љ–Є–љ—Г—З–µ –њ—А–Є–≤–Њ–і–Є—В—М –і–Њ –њ–Њ—П–≤–Є –Љ–∞–≥–љ—Ц—В–љ–Є—Е –њ–Њ–ї—Ц–≤ —З–µ—А–µ–Ј —П–≤–Є—Й–µ –µ–ї–µ–Ї—В—А–Њ–Љ–∞–≥–љ—Ц—В–љ–Њ—Ч —Ц–љ–і—Г–Ї—Ж—Ц—Ч. –Ґ–Њ–Љ—Г —Й–Њ –і—Ц–µ–ї–µ–Ї—В—А–Є–Ї–Є –љ–µ –Љ–∞—О—В—М –Љ–∞–≥–љ—Ц—В–љ—Ц –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц, —В–µ —Ж—Ц–ї–Ї–Њ–Љ –њ—А–Є–њ—Г—Б—В–Є–Љ–Њ –Њ–±–Љ–µ–ґ–Є—В–Є—Б—П —А–Њ–Ј–≥–ї—П–і–Њ–Љ –і—Ц—Ф—О –љ–∞ –і—Ц–µ–ї–µ–Ї—В—А–Є–Ї –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П.
–Ю—Б–љ–Њ–≤–љ–Є–Љ–Є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞–Љ–Є –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П —Ф –є–Њ–≥–Њ –љ–∞–њ—А—Г–ґ–µ–љ—Ц—Б—В—М —Ц –њ–Њ—В–µ–љ—Ж—Ц–∞–ї. –Э–∞–њ—А—Г–ґ–µ–љ—Ц—Б—В—М –њ–Њ–ї—П —Ф –≤–µ–Ї—В–Њ—А–љ–Њ—О –≤–µ–ї–Є—З–Є–љ–Њ—О, –њ–Њ—В–µ–љ—Ж—Ц–∞–ї вАУ —Б–Ї–∞–ї—П—А–љ–Њ—Ч, –Њ–±—Г–Љ–Њ–≤–ї–µ–љ–Њ—Ч –і–µ—П–Ї–Є–Љ —З–Є—Б–ї–Њ–Љ. –Х–ї–µ–Ї—В—А–Є—З–љ–µ –њ–Њ–ї–µ –≤–Є–Ј–љ–∞—З–µ–љ–µ, —П–Ї—Й–Њ –≤—Ц–і–Њ–Љ–Є–є —А–Њ–Ј–њ–Њ–і—Ц–ї –љ–∞–њ—А—Г–ґ–µ–љ–Њ—Б—В—Ц –њ–Њ–ї—П –є –њ–Њ—В–µ–љ—Ж—Ц–∞–ї—Г —Г –≤—Б—Ц—Е —В–Њ—З–Ї–∞—Е —Ж—М–Њ–≥–Њ –њ–Њ–ї—П.
–Х–ї–µ–Ї—В—А–Є—З–љ–µ –њ–Њ–ї–µ –Љ–∞—Ф –Ј–і–∞—В–љ—Ц—Б—В—М –≤–њ–ї–Є–≤–∞—В–Є –љ–∞ –њ–Њ–Љ—Ц—Й–µ–љ–Є–є —Г –љ—М–Њ–≥–Њ –Ј–∞—А—П–і, —Ц–Ј —Б–Є–ї–Њ—О, –њ—А—П–Љ–Њ –њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ—Ц–є –≤–µ–ї–Є—З–Є–љ—Ц —Ж—М–Њ–≥–Њ –Ј–∞—А—П–і—Г. –Т –Њ—Б–љ–Њ–≤—Г –≤–Є–Ј–љ–∞—З–µ–љ–љ—П –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П –њ–Њ–Ї–ї–∞–і–µ–љ–µ –є–Њ–≥–Њ –Љ–µ—Е–∞–љ—Ц—З–љ–Є–є –њ—А–Њ—П–≤, –Њ–њ–Є—Б—Г–≤–∞–љ–µ –Ј–∞–Ї–Њ–љ–Њ–Љ –Ъ—Г–ї–Њ–љ–∞ вАУ ¬Ђ–Ф–≤–∞ —В–Њ—З–Ї–Њ–≤—Ц –Ј–∞—А—П–і–Є –≤–Ј–∞—Ф–Љ–Њ–і—Ц—О—В—М —Ц–Ј —Б–Є–ї–Њ—О, –њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ–Њ—Ч –і–Њ–±—Г—В–Ї—Г –Ј–∞—А—П–і—Ц–≤ —Ц –Њ–±–µ—А–љ–µ–љ–Њ –њ—А–Њ–њ–Њ—А—Ж—Ц–є–љ–Њ—Ч –Ї–≤–∞–і—А–∞—В—Г –≤—Ц–і—Б—В–∞–љ—Ц –Љ—Ц–ґ –љ–Є–Љ–Є¬ї
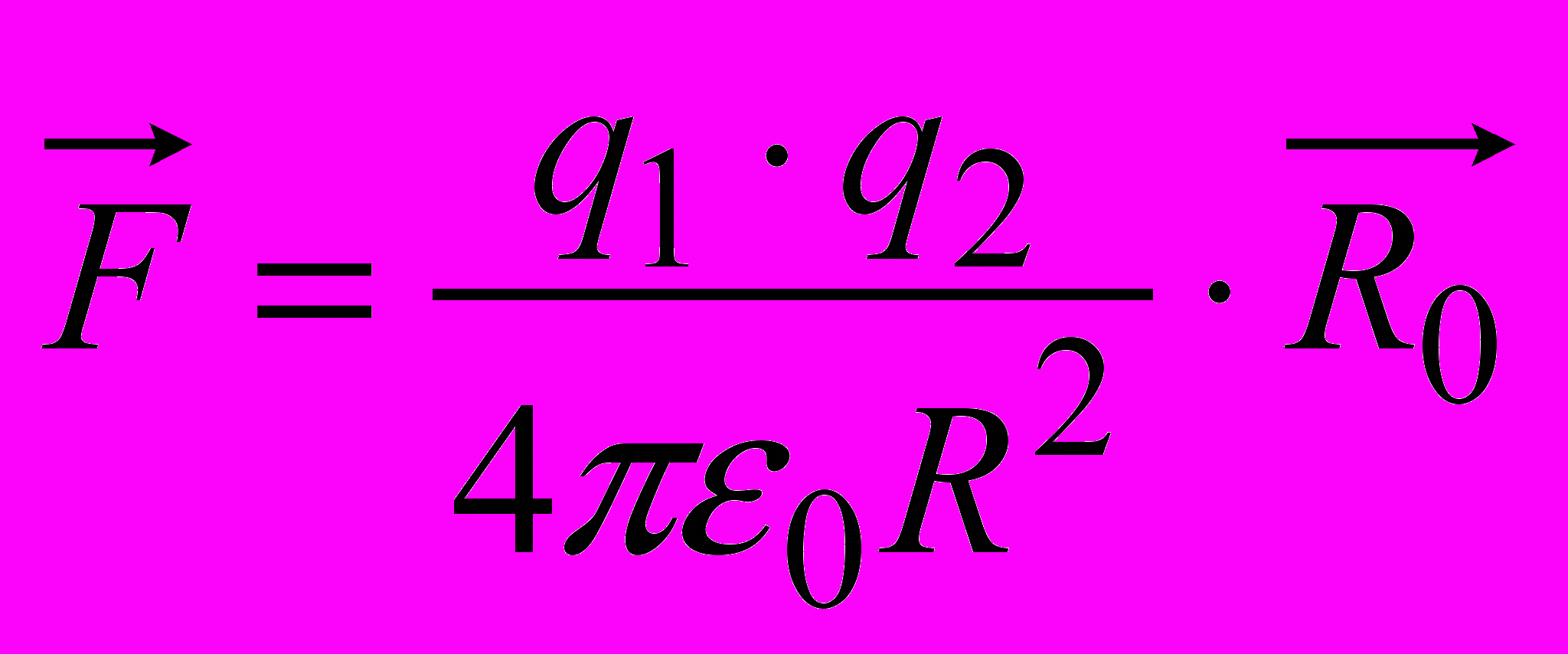
–і–µ
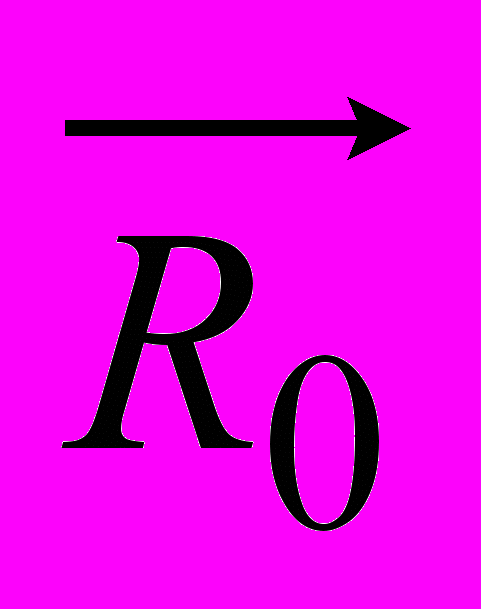 - –Њ–і–Є–љ–Є—З–љ–Є–є –≤–µ–Ї—В–Њ—А, —Б–њ—А—П–Љ–Њ–≤–∞–љ–Є–є —Г–Ј–і–Њ–≤–ґ –ї—Ц–љ—Ц—Ч, —Й–Њ –Ј'—Ф–і–љ—Г—Ф –Ј–∞—А—П–і–Є.
- –Њ–і–Є–љ–Є—З–љ–Є–є –≤–µ–Ї—В–Њ—А, —Б–њ—А—П–Љ–Њ–≤–∞–љ–Є–є —Г–Ј–і–Њ–≤–ґ –ї—Ц–љ—Ц—Ч, —Й–Њ –Ј'—Ф–і–љ—Г—Ф –Ј–∞—А—П–і–Є.–Х–ї–µ–Ї—В—А–Є—З–љ–µ –њ–Њ–ї–µ –Љ–Њ–ґ–љ–∞ –Њ—Е–∞—А–∞–Ї—В–µ—А–Є–Ј—Г–≤–∞—В–Є —Б—Г–Ї—Г–њ–љ—Ц—Б—В—О —Б–Є–ї–Њ–≤–Є—Е —Ц –µ–Ї–≤—Ц–њ–Њ—В–µ–љ—Ж—Ц–∞–ї—М–љ–Є—Е –ї—Ц–љ—Ц–є. –°–Є–ї–Њ–≤–∞ –ї—Ц–љ—Ц—П –≤–Є–Ј–љ–∞—З–∞—Ф, —П–Ї –±–Є —А—Г—Е–∞–≤—Б—П –і–Њ—Б–Є—В—М –Љ–∞–ї–Є–є –њ–Њ–Ј–Є—В–Є–≤–љ–Є–є –Ј–∞—А—П–і, —Й–Њ –љ–µ –≤–Њ–ї–Њ–і—Ц—Ф —Ц–љ–µ—А—Ж—Ц—Ф—О. –°–Є–ї–Њ–≤—Ц –ї—Ц–љ—Ц—Ч –њ–Њ—З–Є–љ–∞—О—В—М—Б—П –љ–∞ –љ–µ–≥–∞—В–Є–≤–љ–Є—Е –Ј–∞—А—П–і–∞—Е —Ц –Ј–∞–Ї—Ц–љ—З—Г—О—В—М—Б—П –љ–∞ –њ–Њ–Ј–Є—В–Є–≤–љ—Ц.
–Х–Ї–≤—Ц–њ–Њ—В–µ–љ—Ж—Ц–∞–ї—М–љ–Є–Љ–Є –љ–∞–Ј–Є–≤–∞—О—В—М –њ–Њ–≤–µ—А—Е–љ—Ц, —Й–Њ –Љ–∞—О—В—М —А—Ц–≤–љ–Є–є –њ–Њ—В–µ–љ—Ж—Ц–∞–ї. –њ–µ—А–µ—В–Є–љ–∞–љ–љ—П –µ–Ї–≤—Ц–њ–Њ—В–µ–љ—Ж—Ц–∞–ї—М–љ–Є—Е –њ–Њ–≤–µ—А—Е–Њ–љ—М —Ц–Ј —Б—Ц—З–љ–Њ—О –њ–ї–Њ—Й–Є–љ–Њ—О –і–∞—Ф –љ–∞–Љ –µ–Ї–≤—Ц–њ–Њ—В–µ–љ—Ж—Ц–∞–ї—М–љ—Ц –ї—Ц–љ—Ц—Ч.
–Я–Њ—В–µ–љ—Ж—Ц–∞–ї ѕЖ –њ–Њ–ї—П –Љ–Њ–ґ–љ–∞ –≤–Є–Ј–љ–∞—З–Є—В–Є —П–Ї —А–Њ–±–Њ—В—Г –Ј –њ–µ—А–µ–љ–Њ—Б—Г –Њ–і–Є–љ–Є—З–љ–Њ–≥–Њ –њ–Њ–Ј–Є—В–Є–≤–љ–Њ–≥–Њ –Ј–∞—А—П–і—Г –Ј –і–∞–љ–Њ—Ч —В–Њ—З–Ї–Є –≤ —В–Њ—З–Ї—Г –Ј –љ—Г–ї—М–Њ–≤–Є–Љ –њ–Њ—В–µ–љ—Ж—Ц–∞–ї–Њ–Љ. –Ґ–Њ—З–Ї–∞ –Ј –љ—Г–ї—М–Њ–≤–Є–Љ –њ–Њ—В–µ–љ—Ж—Ц–∞–ї–Њ–Љ –≤–Є–±–Є—А–∞—Ф—В—М—Б—П –і–Њ–≤—Ц–ї—М–љ–Њ.
–Я–Њ—В–µ–љ—Ж—Ц–∞–ї —Ц –љ–∞–њ—А—Г–ґ–µ–љ—Ц—Б—В—М –њ–Њ–ї—П –Ј–≤'—П–Ј–∞–љ—Ц –Љ—Ц–ґ —Б–Њ–±–Њ—О –Ј–∞–≥–∞–ї—М–љ–Є–Љ —А—Ц–≤–љ—П–љ–љ—П–Љ
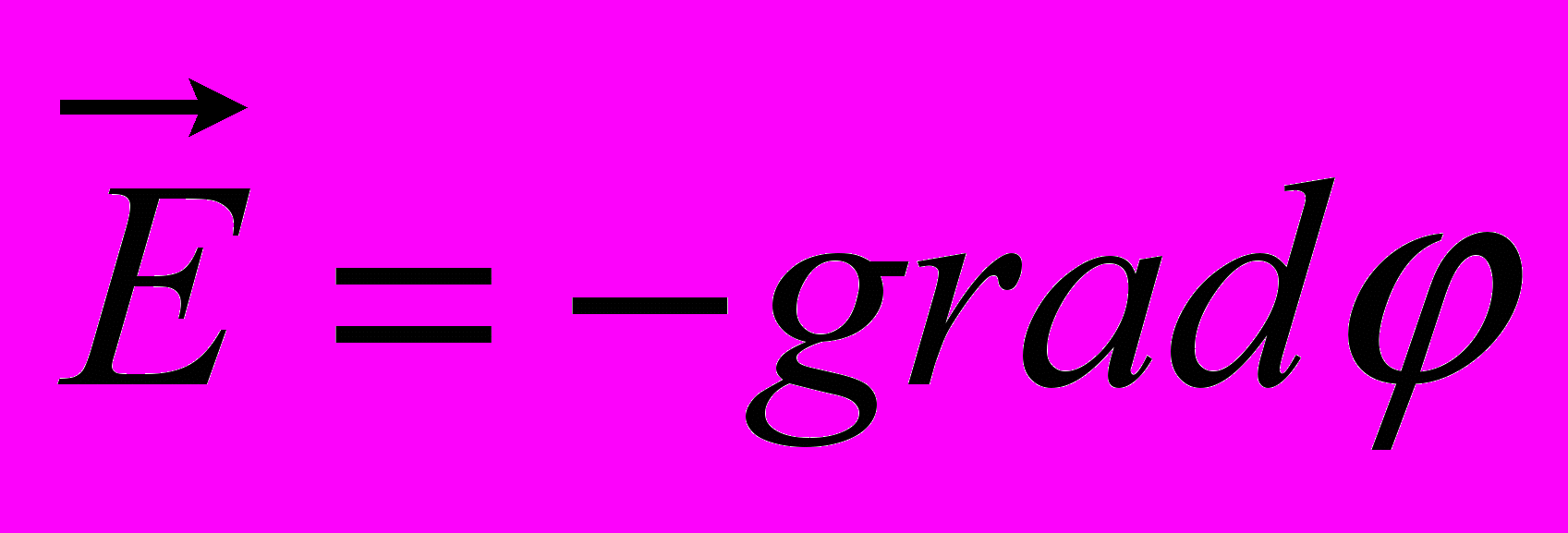
–Х–ї–µ–Ї—В—А–Є—З–љ–µ –њ–Њ–ї–µ —Ф –њ–Њ—В–µ–љ—Ж—Ц–є–љ–Є–Љ. –¶–µ –њ–Њ–Ј–љ–∞—З–∞—Ф, —Й–Њ —А–Њ–±–Њ—В–∞ –Ј –њ–µ—А–µ–Љ—Ц—Й–µ–љ–љ—П –Ј–∞—А—П–і—Г –≤ —Ж—М–Њ–Љ—Г –њ–Њ–ї—Ц –љ–µ –Ј–∞–ї–µ–ґ–Є—В—М –≤—Ц–і –і–Њ–≤–ґ–Є–љ–Є —В—А–∞—Ф–Ї—В–Њ—А—Ц—Ч, –∞ –≤–Є–Ј–љ–∞—З–∞—Ф—В—М—Б—П —В—Ц–ї—М–Ї–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є –њ–Њ—З–∞—В–Ї–Њ–≤–Њ—Ч –є –Ї—Ц–љ—Ж–µ–≤–Њ—Ч —В–Њ—З–Њ–Ї —В—А–∞—Ф–Ї—В–Њ—А—Ц—Ч. –Ч–Њ–Ї—А–µ–Љ–∞, —А–Њ–±–Њ—В–∞ –Ј –њ–µ—А–µ–Љ—Ц—Й–µ–љ–љ—П –Ј–∞—А—П–і—Г –њ–Њ –Ј–∞–Љ–Ї–љ–µ–љ–Њ–Љ—Г –Ї–Њ–љ—В—Г—А—Г —А—Ц–≤–љ—П—Ф—В—М—Б—П –љ—Г–ї—О.
–Ф
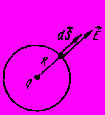
–†–Є—Б. 5.1. –Ф–Њ —А–Њ–Ј—А–∞—Е—Г–љ–Ї—Г
–µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П
—В–Њ—З–Ї–Њ–≤–Њ–≥–Њ –Ј–∞—А—П–і—Г.
–ї—П —А–Њ–Ј—А–∞—Е—Г–љ–Ї—Ц–≤ –љ–∞–њ—А—Г–ґ–µ–љ–Њ—Б—В—Ц –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П, —Б—В–≤–Њ—А—О–≤–∞–љ–Њ–≥–Њ —Б–Є—Б—В–µ–Љ–Њ—О –Ј–∞—А—П–і—Ц–≤, –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—В—М —В–µ–Њ—А–µ–Љ—Г –У–∞—Г—Б–∞, —П–Ї–∞ —Д–Њ—А–Љ—Г–ї—О—Ф—В—М—Б—П –≤ —В–∞–Ї–Є–є —Б–њ–Њ—Б—Ц–± : –њ–Њ—В—Ц–Ї –≤–µ–Ї—В–Њ—А–∞ –љ–∞–њ—А—Г–ґ–µ–љ–Њ—Б—В—Ц –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П —З–µ—А–µ–Ј –±—Г–і—М-—П–Ї—Г –Ј–∞–Љ–Ї–љ–µ–љ—Г –њ–Њ–≤–µ—А—Е–љ—О –і–Њ—А—Ц–≤–љ—О—Ф —Б—Г–Љ—Ц –≤—Ц–ї—М–љ–Є—Е –Ј–∞—А—П–і—Ц–≤, —Й–Њ –њ–µ—А–µ–±—Г–≤–∞—О—В—М —Г—Б–µ—А–µ–і–Є–љ—Ц —Ж—Ц—Ф—Ч –њ–Њ–≤–µ—А—Е–љ—Ц, –і—Ц–ї–µ–љ–µ –љ–∞ –і–Њ–±—Г—В–Њ–Ї ќµ0вИЩќµ. –Ґ—Г—В ќµ вАУ –і—Ц–µ–ї–µ–Ї—В—А–Є—З–љ–∞ –њ—А–Њ–љ–Є–Ї–љ—Ц—Б—В—М —А–µ—З–Њ–≤–Є–љ–Є, ќµ0 = 8,84вИЩ10-12 –§/–Љ вАУ –µ–ї–µ–Ї—В—А–Є—З–љ–∞ –њ–Њ—Б—В—Ц–є–љ–∞.
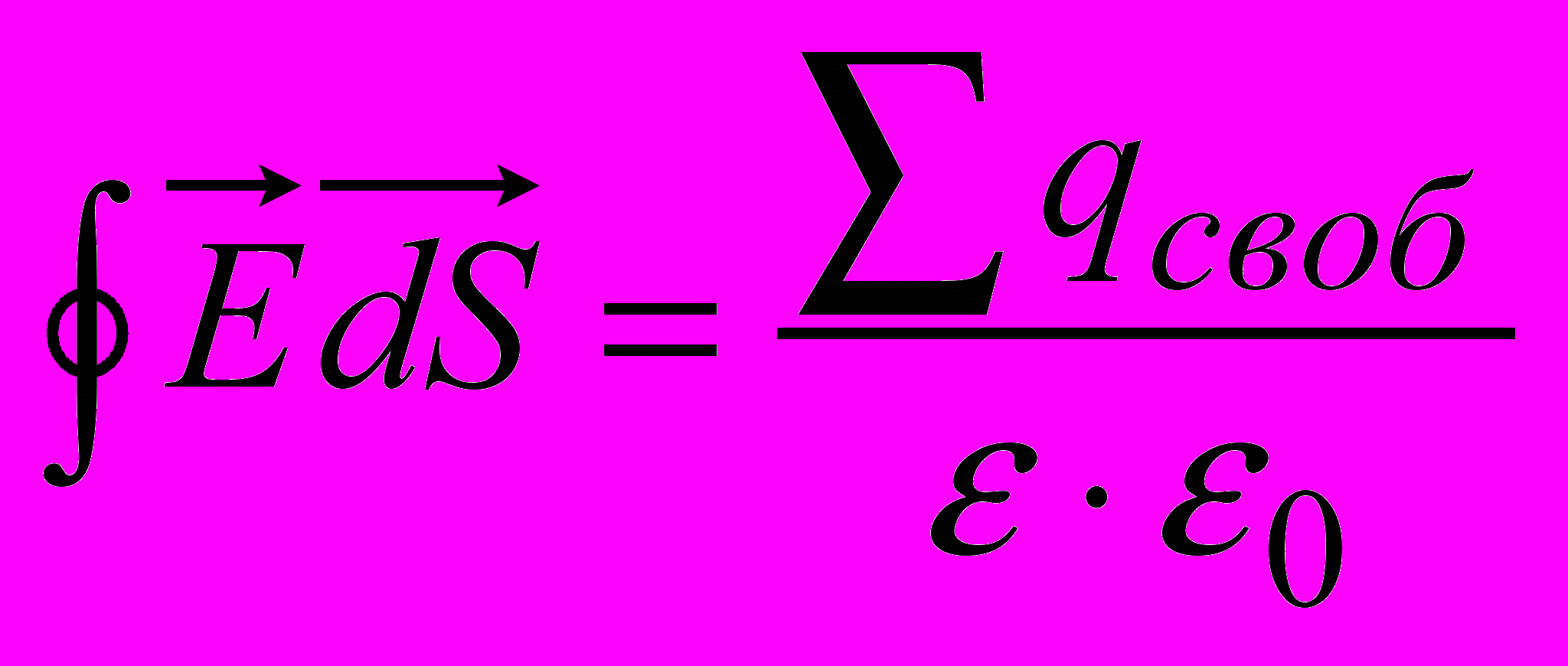
^
5.2.1. –Х–ї–µ–Ї—В—А–Є—З–љ–µ –њ–Њ–ї–µ —В–Њ—З–Ї–Њ–≤–Њ–≥–Њ –Ј–∞—А—П–і—Г.
–Ґ–µ–Њ—А–µ–Љ—Г –У–∞—Г—Б—Б–∞ –Ј—А—Г—З–љ–Њ –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г–≤–∞—В–Є –і–ї—П –≤–Є–Ј–љ–∞—З–µ–љ–љ—П –љ–∞–њ—А—Г–ґ–µ–љ–Њ—Б—В—Ц –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П, —П–Ї—Й–Њ —З–µ—А–µ–Ј –Ј–∞–і–∞–љ—Г —В–Њ—З–Ї—Г –ї–µ–≥–Ї–Њ –њ—А–Њ–≤–µ—Б—В–Є –њ–Њ–≤–µ—А—Е–љ—П, —Г—Б—Ц —В–Њ—З–Ї–Є —П–Ї–Њ—Ч –±—Г–і—Г—В—М —Г —Б–Є–Љ–µ—В—А–Є—З–љ–Є—Е —Г–Љ–Њ–≤–∞—Е —Й–Њ–і–Њ –Ј–∞—А—П–і—Г. –Ґ–∞–Ї–Њ—О –њ–Њ–≤–µ—А—Е–љ–µ—О –Ј–≤–Є—З–∞–є–љ–Њ —Ф —Б—Д–µ—А–∞ –і–ї—П —В–Њ—З–Ї–Њ–≤–Є—Е –Ј–∞—А—П–і—Ц–≤ –∞–±–Њ —Ж–Є–ї—Ц–љ–і—А –і–ї—П –ї—Ц–љ—Ц–є–љ–Є—Е –Ј–∞—А—П–і—Ц–≤ (–і–Њ–≤–≥–Є—Е –њ—А–Њ–≤—Ц–і–љ–Є–Ї—Ц–≤).
–ѓ–Ї –њ—А–Є–Ї–ї–∞–і –Ј–љ–∞–є–і–µ–Љ–Њ –љ–∞–њ—А—Г–ґ–µ–љ—Ц—Б—В—М –њ–Њ–ї—П, —Б—В–≤–Њ—А—О–≤–∞–љ–Њ–≥–Њ —В–Њ—З–Ї–Њ–≤–Є–Љ –Ј–∞—А—П–і–Њ–Љ —Г —В–Њ—З—Ж—Ц, –≤—Ц–і–і–∞–ї–µ–љ–Њ—Ч –љ–∞ –≤—Ц–і—Б—В–∞–љ—М ^ R –≤—Ц–і –Ј–∞—А—П–і—Г. –І–µ—А–µ–Ј –Ј–∞–і–∞–љ—Г —В–Њ—З–Ї—Г –њ—А–Њ–≤–µ–і–µ–Љ–Њ —Б—Д–µ—А—Г –Ј —А–∞–і—Ц—Г—Б–Њ–Љ R —Ц —Ж–µ–љ—В—А–Њ–Љ —Г —В–Њ—З—Ж—Ц —А–Њ–Ј—В–∞—И—Г–≤–∞–љ–љ—П –Ј–∞—А—П–і—Г q. –Т–µ–Ї—В–Њ—А, —Й–Њ –Ј–Њ–±—А–∞–ґ—Г—Ф –µ–ї–µ–Љ–µ–љ—В –њ–Њ–≤–µ—А—Е–љ—Ц —Б—Д–µ—А–Є ds –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є–є –њ–Њ–≤–µ—А—Е–љ—Ц —Б—Д–µ—А–Є –є –њ–Њ –љ–∞–њ—А—П–Љ–Ї–Њ–≤—Ц –Ј–∞–≤–ґ–і–Є –Ј–±—Ц–≥–∞—Ф—В—М—Б—П –Ј –≤–µ–Ї—В–Њ—А–Њ–Љ –љ–∞–њ—А—Г–ґ–µ–љ–Њ—Б—В—Ц –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П E. –ѓ–Ї—Й–Њ –≤—А–∞—Е—Г–≤–∞—В–Є, —Й–Њ –љ–∞–њ—А—Г–ґ–µ–љ—Ц—Б—В—М –њ–Њ–ї—П E –Њ–і–љ–∞–Ї–Њ–≤–∞ —Г –≤—Б—Ц—Е —В–Њ—З–Ї–∞—Е —Б—Д–µ—А–Є, —В–Њ E —П–Ї –Ї–Њ–љ—Б—В–∞–љ—В—Г –Љ–Њ–ґ–љ–∞ –≤–Є–љ–µ—Б—В–Є –Ј–∞ –Ј–љ–∞–Ї —Ц–љ—В–µ–≥—А–∞–ї–∞:
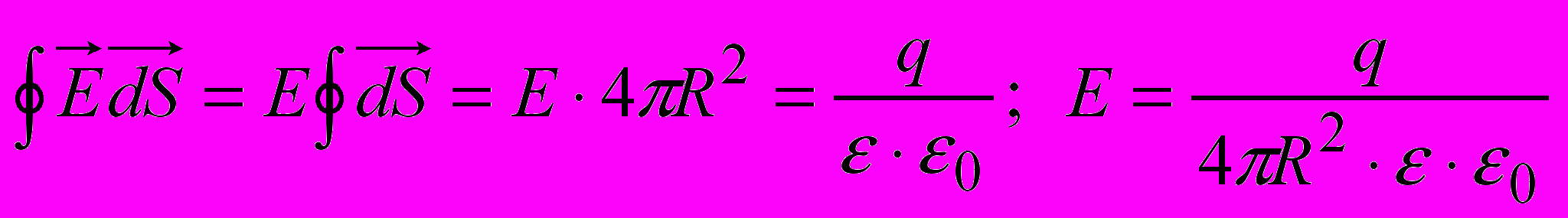
–Ч–љ–∞–є–і–µ–Љ–Њ –≤–Є—А–∞–Ј –і–ї—П –њ–Њ—В–µ–љ—Ж—Ц–∞–ї—Г –њ–Њ–ї—П —В–Њ—З–Ї–Њ–≤–Њ–≥–Њ –Ј–∞—А—П–і—Г. –°–Ї–Њ—А–Є—Б—В–∞—Ф–Љ–Њ—Б—П —Б—Д–µ—А–Є—З–љ–Њ—О —Б–Є—Б—В–µ–Љ–Њ—О –Ї–Њ–Њ—А–і–Є–љ–∞—В. –£ —Б–Є–ї—Г —Б—Д–µ—А–Є—З–љ–Њ—Ч —Б–Є–Љ–µ—В—А—Ц—Ч –љ–∞–њ—А—Г–ґ–µ–љ—Ц—Б—В—М –њ–Њ–ї—П –±—Г–і–µ –Љ–∞—В–Є —В—Ц–ї—М–Ї–Є –Њ–і–љ—Г —Б–Ї–ї–∞–і–Њ–≤—Г —Г–Ј–і–Њ–≤–ґ –Њ—Б—Ц R. –Ж–Ј –Ј–∞–≥–∞–ї—М–љ–Њ–≥–Њ —А—Ц–≤–љ—П–љ–љ—П –і–ї—П –≤–Є–Ј–љ–∞—З–µ–љ–љ—П –њ–Њ—В–µ–љ—Ж—Ц–∞–ї—Г –≤–Є–њ–ї–Є–≤–∞—Ф, —Й–Њ
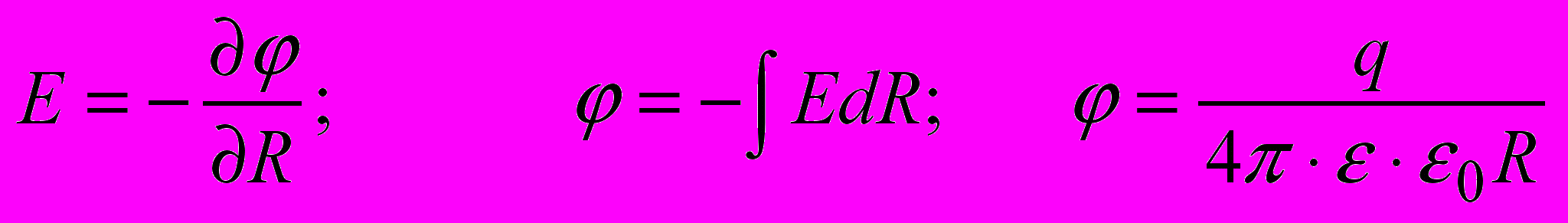
^
5.2.2. –Х–ї–µ–Ї—В—А–Є—З–љ–µ –њ–Њ–ї–µ –Ј–∞—А—П–і–ґ–µ–љ–Њ—Ч –Њ—Б—Ц.
–Я
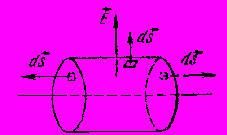
–†–Є—Б. 5.2. –Ф–Њ —А–Њ–Ј—А–∞—Е—Г–љ–Ї—Г –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П –Ј–∞—А—П–і–ґ–µ–љ–Њ—Ч –Њ—Б—Ц.
—Ц–і –Ј–∞—А—П–і–ґ–µ–љ–Њ—О –≤—Ц—Б—Б—О —А–Њ–Ј—Г–Љ—Ц—О—В—М —В–µ–Њ—А–µ—В–Є—З–љ–Њ –љ–µ—Б–Ї—Ц–љ—З–µ–љ–љ–Њ –і–Њ–≤–≥–Є–є –њ—А–Њ–≤—Ц–і–љ–Є–Ї. –Ч–∞—А—П–і –љ–∞ –Њ–і–Є–љ–Є—Ж—О –і–Њ–≤–ґ–Є–љ–Є –Њ—Б—Ц –њ—А–Є–є–Љ–µ–Љ–Њ —А—Ц–≤–љ–Є–Љ ѕД. –Ф–ї—П –Ј–љ–∞—Е–Њ–і–ґ–µ–љ–љ—П –љ–∞–њ—А—Г–ґ–µ–љ–Њ—Б—В—Ц –њ–Њ–ї—П –≤ —В–Њ—З—Ж—Ц, —А–Њ–Ј—В–∞—И–Њ–≤–∞–љ–Њ—Ч –љ–∞ –≤—Ц–і—Б—В–∞–љ—Ц r –≤—Ц–і –Њ—Б—Ц, –њ—А–Њ–≤–µ–і–µ–Љ–Њ —З–µ—А–µ–Ј —Ж—О —В–Њ—З–Ї—Г —Ж–Є–ї—Ц–љ–і—А–Є—З–љ—Г –њ–Њ–≤–µ—А—Е–љ—О —В–∞–Ї, —Й–Њ–± –≤—Ц—Б—М —Ж—М–Њ–≥–Њ —Ж–Є–ї—Ц–љ–і—А–∞ –Ј–±—Ц–≥–∞–ї–∞—Б—П —Ц–Ј –Ј–∞—А—П–і–ґ–µ–љ–Њ—О –≤—Ц—Б—Б—О. –Ч –Љ—Ц—А–Ї—Г–≤–∞–љ—М —Б–Є–Љ–µ—В—А—Ц—Ч —П—Б–љ–Њ, —Й–Њ –љ–∞–њ—А—Г–ґ–µ–љ—Ц—Б—В—М –њ–Њ–ї—П —Г –≤—Б—Ц—Е —В–Њ—З–Ї–∞—Е —Ж–Є–ї—Ц–љ–і—А–Є—З–љ–Њ—Ч –њ–Њ–≤–µ—А—Е–љ—Ц –±—Г–і–µ –Њ–і–љ–∞–Ї–Њ–≤–Њ—О. –Ч–∞–Љ–Ї–љ–µ–љ–∞ –њ–Њ–≤–µ—А—Е–љ—П —Г—В–≤–Њ—А—О—Ф—В—М—Б—П –±—Ц—З–љ–Њ—О –њ–Њ–≤–µ—А—Е–љ–µ—О –є –і–≤–Њ–Љ–∞ –і–µ–љ—Ж—П–Љ–Є —Ж–Є–ї—Ц–љ–і—А–∞. –Э–∞ –њ–Њ–≤–µ—А—Е–љ—Ц —Ж–Є–ї—Ц–љ–і—А–∞ –≤–µ–Ї—В–Њ—А, —Й–Њ –Ј–Њ–±—А–∞–ґ—Г—Ф –µ–ї–µ–Љ–µ–љ—В –њ–Њ–≤–µ—А—Е–љ—Ц —Ж–Є–ї—Ц–љ–і—А–∞ ds –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є–є –њ–Њ–≤–µ—А—Е–љ—Ц —Ж–Є–ї—Ц–љ–і—А–∞ –є –њ–Њ –љ–∞–њ—А—П–Љ–Ї–Њ–≤—Ц –Ј–∞–≤–ґ–і–Є –Ј–±—Ц–≥–∞—Ф—В—М—Б—П –Ј –≤–µ–Ї—В–Њ—А–Њ–Љ –љ–∞–њ—А—Г–ґ–µ–љ–Њ—Б—В—Ц –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П E. –Я–Њ—В—Ц–Ї –≤–µ–Ї—В–Њ—А–∞ E —З–µ—А–µ–Ј –і–µ–љ—Ж—П —Ж–Є–ї—Ц–љ–і—А–∞ –≤—Ц–і—Б—Г—В–љ—Ц–є, —В–Њ–Љ—Г —Й–Њ –µ–ї–µ–Љ–µ–љ—В –њ–Њ–≤–µ—А—Е–љ—Ц –і–µ–љ—Ж—П –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є–є –≤–µ–Ї—В–Њ—А—Г –љ–∞–њ—А—Г–ґ–µ–љ–Њ—Б—В—Ц –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П E.
–Т–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—З–Є —В–µ–Њ—А–µ–Љ—Г –У–∞—Г—Б–∞ –Њ–і–µ—А–ґ—Г—Ф–Љ–Њ:
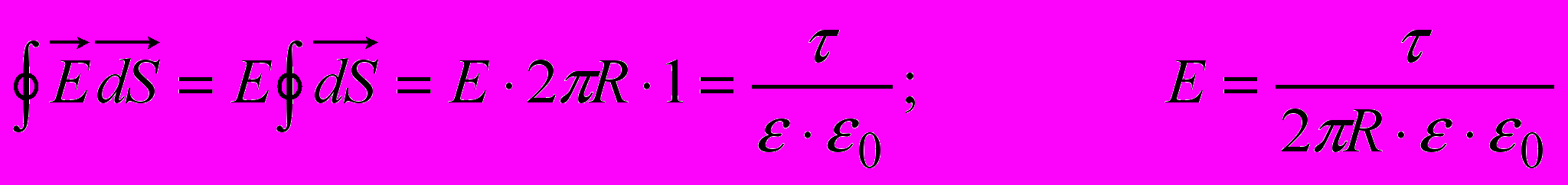
–Ь–Є –Њ–±—З–Є—Б–ї—О—Ф–Љ–Њ –њ–Њ–≤–µ—А—Е–љ—О —Ж–Є–ї—Ц–љ–і—А–∞ –Њ–і–Є–љ–Є—З–љ–Њ—Ч –і–Њ–≤–ґ–Є–љ–Є –є –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—Ф–Љ–Њ –Ј–∞—А—П–і, —Й–Њ –і–Њ–≤–Њ–і–Є—В—М—Б—П –љ–∞ —В—Г –ґ –Њ–і–Є–љ–Є—Ж—О –і–Њ–≤–ґ–Є–љ–Є.
^
5.2.3. –Х–ї–µ–Ї—В—А–Є—З–љ–µ –њ–Њ–ї–µ –і–Є–њ–Њ–ї—П.
–°—Е–µ–Љ–∞—В–Є—З–љ–Њ –µ–ї–µ–Ї—В—А–Є—З–љ–Є–є –і–Є–њ–Њ–ї—М –Ј–Њ–±—А–∞–ґ–µ–љ–Є–є —А–Є—Б. 5.3.
–£ —Б–Є–ї—Г –њ—А–Є–љ—Ж–Є–њ—Г —Б—Г–њ–µ—А–њ–Њ–Ј–Є—Ж—Ц—Ч –≤–Є–Ј–љ–∞—З–Є–Љ–Њ –њ–Њ—В–µ–љ—Ж—Ц–∞–ї —В–Њ—З–Ї–Є a —П–Ї –њ–Њ—В–µ–љ—Ж—Ц–∞–ї —Г –њ–Њ–ї–µ –і–≤–Њ—Е —В–Њ—З–Ї–Њ–≤–Є—Е –Ј–∞—А—П–і—Ц–≤.
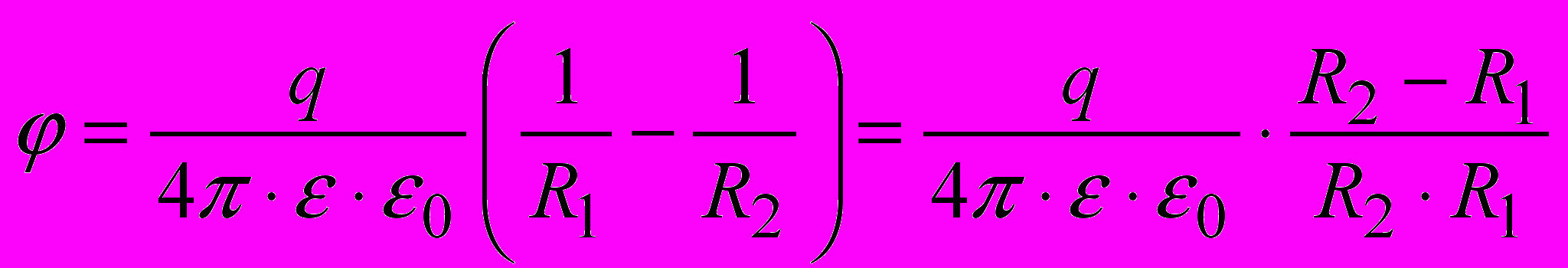
–ѓ–Ї—Й–Њ R>>l, —В–Њ –Љ–Њ–ґ–љ–∞ –≤–≤–∞–ґ–∞—В–Є R1вИЩR2 = R2.
–Ґ–Њ–і—Ц –Њ–і–µ—А–ґ–Є–Љ–Њ –≤–Є—А–∞–Ј –і–ї—П –њ–Њ—В–µ–љ—Ж—Ц–∞–ї—Г —В–Њ—З–Ї–Є –∞ –≤ –љ–∞—Б—В—Г–њ–љ–Њ–Љ—Г –≤–Є–і—Ц:
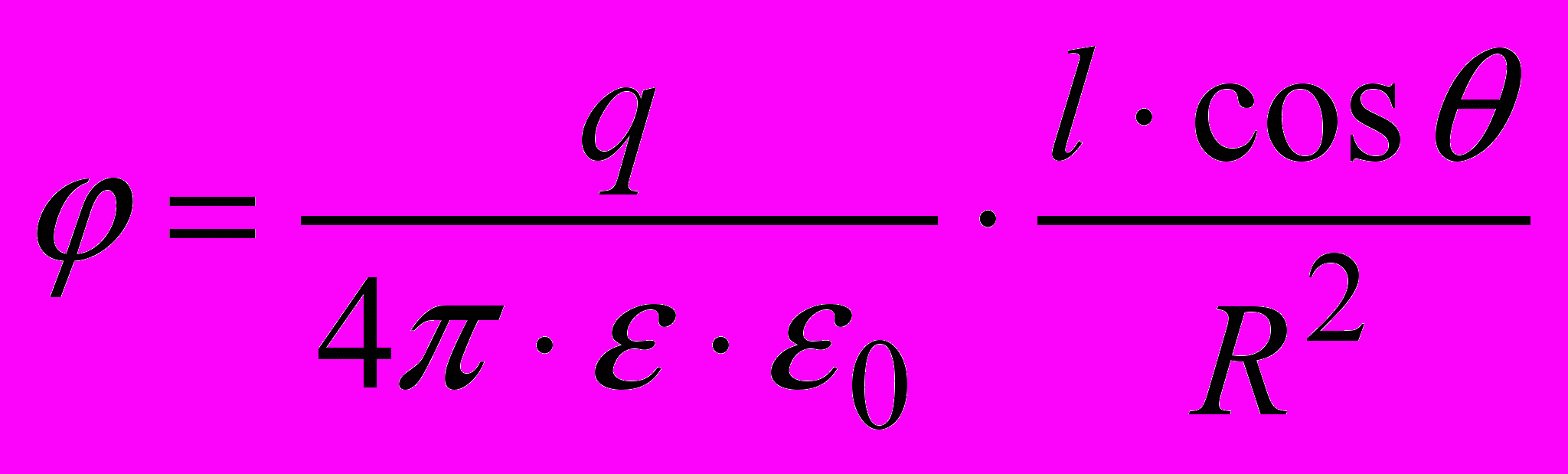
–°–Ї–Њ—А–Є—Б—В–∞—Ф–Љ–Њ—Б—П —Б—Д–µ—А–Є—З–љ–Њ—О —Б–Є—Б—В–µ–Љ–Њ—О –Ї–Њ–Њ—А–і–Є–љ–∞—В —Ц–Ј —Ж–µ–љ—В—А–Њ–Љ —Г —Б–µ—А–µ–і–Є–љ—Ц –і–Є–њ–Њ–ї—П. –Ю–і–µ—А–ґ–Є–Љ–Њ –≤–Є—А–∞–Ј–Є –і–ї—П —Б–Ї–ї–∞–і–Њ–≤–Є—Е –љ–∞–њ—А—Г–ґ–µ–љ–Њ—Б—В—Ц –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П:
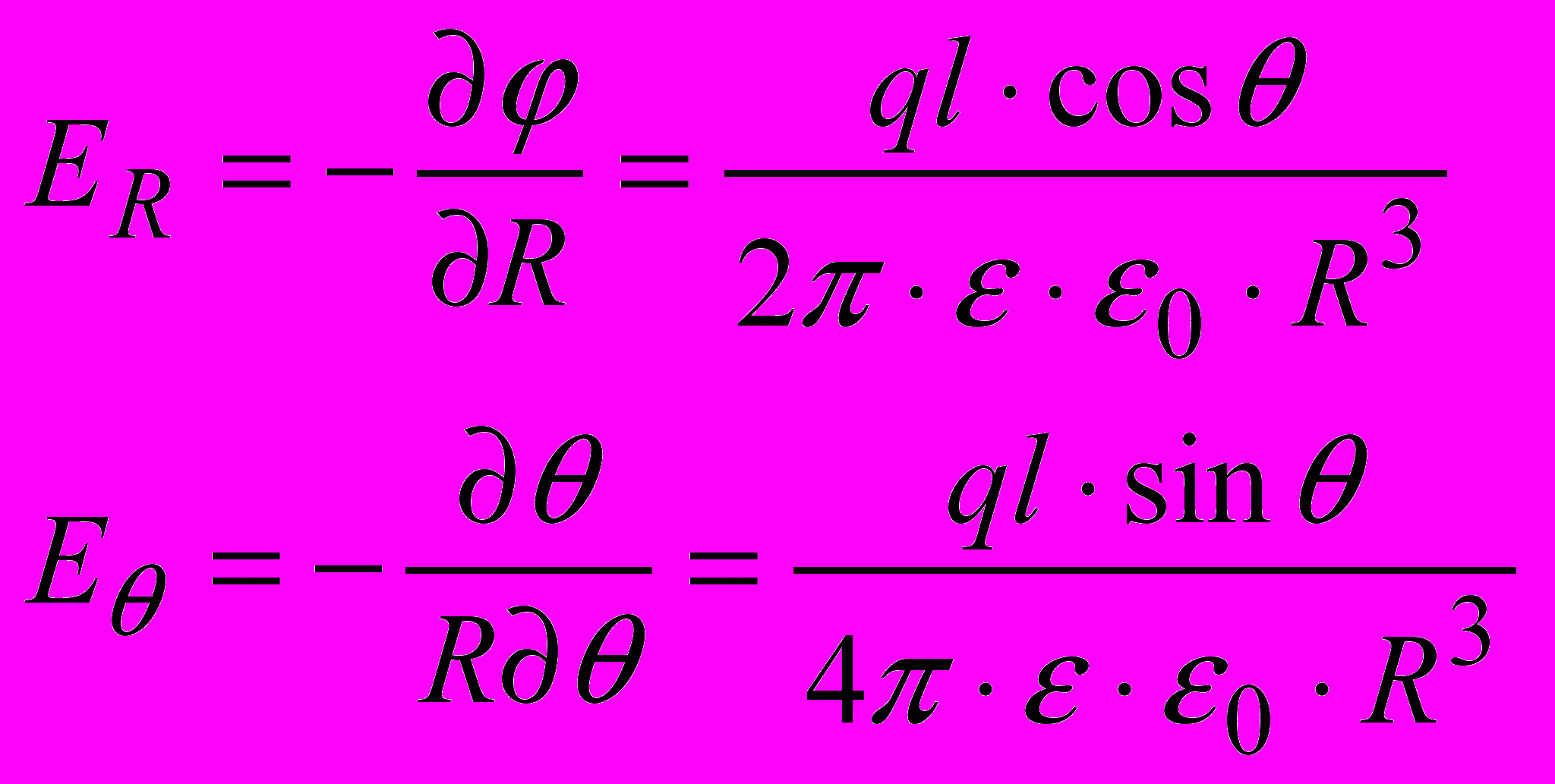
–Ґ–Њ–і—Ц –љ–∞–њ—А—Г–ґ–µ–љ—Ц—Б—В—М –њ–Њ–ї—П –≤ —В–Њ—З—Ж—Ц –∞ –Њ–±—З–Є—Б–ї—О—Ф–Љ–Њ —П–Ї
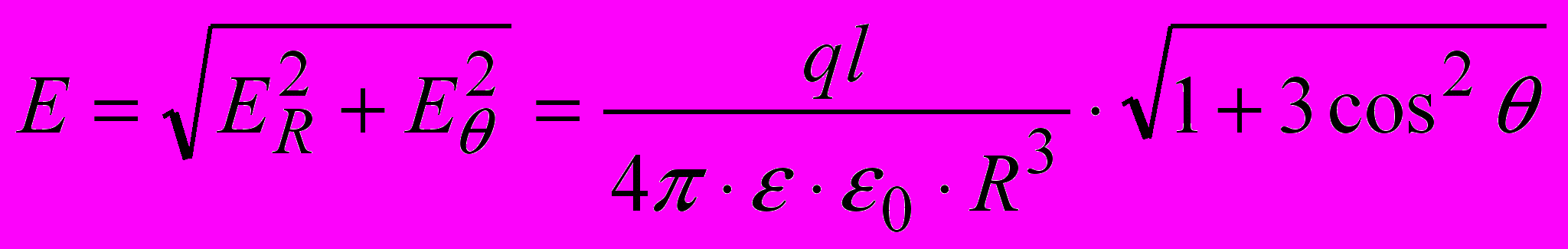
–†
–†–Є—Б. 5.3. –Ф–Њ —А–Њ–Ј—А–∞—Е—Г–љ–Ї—Г –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П –і–Є–њ–Њ–ї—П.
–µ–Ј—Г–ї—М—В—Г—О—З–∞ –Ї–∞—А—В–Є–љ–∞ –њ–Њ–ї—П –Ј–Њ–±—А–∞–ґ–µ–љ–∞ –љ–∞ —А–Є—Б.5.4.
–Ф–ї—П —А–Њ–Ј—Г–Љ—Ц–љ–љ—П –њ—А–Њ—Ж–µ—Б—Ц–≤ —Г –і—Ц–µ–ї–µ–Ї—В—А–Є–Ї–∞—Е –≤–∞–ґ–ї–Є–≤–Њ –Ј–љ–∞—В–Є —В–Є–њ–Њ–≤—Ц —А–Њ–Ј–њ–Њ–і—Ц–ї–Є –є –Ј–љ–∞—З–µ–љ–љ—П –њ–Њ–ї—Ц–≤. –Э–∞–є–±—Ц–ї—М—И–µ —З–∞—Б—В–Њ –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—О—В—М—Б—П –Љ–Њ–і–µ–ї—М–љ—Ц –≤–Є—Б—В–∞–≤–Є –µ–ї–µ–Ї—В—А–Њ–і–љ–Є—Е —Б–Є—Б—В–µ–Љ, –і–Њ —П–Ї–Є—Е –Ј —В—Ц—Ф—Ч –∞–±–Њ —Ц–љ—И–Є–Љ —Б—В—Г–њ–µ–љ–µ–Љ –љ–∞–±–ї–Є–ґ–µ–љ–љ—П –Љ–Њ–ґ–љ–∞ –Ј–≤–µ—Б—В–Є –±–∞–≥–∞—В–Њ —А–µ–∞–ї—М–љ—Ц –µ–ї–µ–Ї—В—А–Њ–і–љ—Ц —Б–Є—Б—В–µ–Љ–Є.
–¶–µ –і–≤–∞ —В–Є–њ–Є –њ–Њ–ї—Ц–≤: –њ–ї–∞—Б–Ї–Њ вАУ –њ–∞—А–∞–ї–µ–ї—М–љ–µ –є —А–∞–і—Ц–∞–ї—М–љ–Њ-—Ж–Є–ї—Ц–љ–і—А–Є—З–љ–µ, –∞–±–Њ –∞–Ї—Б—Ц–∞–ї—М–љ–µ. –Э–Є–ґ—З–µ –њ—А–Є–≤–Њ–і–Є—В—М—Б—П –Њ–њ–Є—Б —Ж–Є—Е –њ–Њ–ї—Ц–≤ —Ц –љ–µ–Њ–±—Е—Ц–і–љ—Ц –і–ї—П —А–Њ–Ј—А–∞—Е—Г–љ–Ї—Ц–≤ —Д–Њ—А–Љ—Г–ї–Є.
–Я
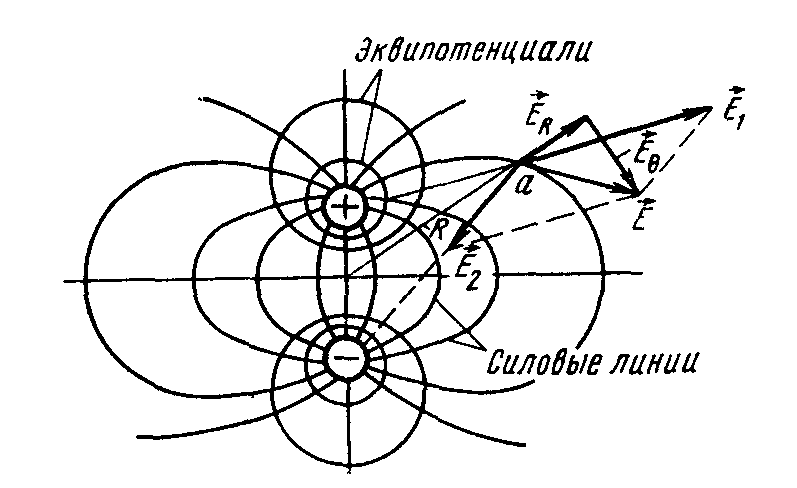
–†–Є—Б. 5.4. –Ъ–∞—А—В–Є–љ–∞ –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П –і–Є–њ–Њ–ї—П
–ї–Њ—Б–Ї–Њ–њ–∞—А–∞–ї–µ–ї—М–љ–µ –њ–Њ–ї–µ. –Ґ—Г—В –µ–Ї–≤—Ц–њ–Њ—В–µ–љ—Ж—Ц–∞–ї—М–љ—Ц –њ–Њ–≤–µ—А—Е–љ—Ц (–њ–Њ–≤–µ—А—Е–љ—Ц —А—Ц–≤–љ—П) —П–≤–ї—П—О—В—М —Б–Њ–±–Њ—О –њ–∞—А–∞–ї–µ–ї—М–љ—Ц –њ–ї–Њ—Й–Є–љ–Є. –Э–∞–њ—А—Г–ґ–µ–љ—Ц—Б—В—М –њ–Њ–ї—П –±—Г–і–µ –Њ–і–љ–∞–Ї–Њ–≤–Њ—Ч —Г –≤—Б—Ц—Е —В–Њ—З–Ї–∞—Е. –Я—А–∞–Ї—В–Є—З–љ–Њ —В–∞–Ї–µ –њ–Њ–ї–µ –Љ–Њ–ґ–љ–∞ —Б–њ–Њ—Б—В–µ—А—Ц–≥–∞—В–Є –≤ –њ–ї–Њ—Б–Ї–Є—Е –Ї–Њ–љ–і–µ–љ—Б–∞—В–Њ—А–∞—Е, —П–Ї—Й–Њ –Ј–љ–µ–≤–∞–ґ–Є—В–Є –≤–њ–ї–Є–≤–Њ–Љ –Ї—А–∞–є–Њ–≤–Є—Е –µ—Д–µ–Ї—В—Ц–≤. –Д–Љ–љ—Ц—Б—В—М –њ–ї–Њ—Б–Ї–Њ–≥–Њ –Ї–Њ–љ–і–µ–љ—Б–∞—В–Њ—А–∞ –Љ–Њ–ґ–љ–∞ –Њ–±—З–Є—Б–ї–Є—В–Є —П–Ї –Ч= ќµќµ0вИЩS/d. –Ґ—Г—В S вАУ –њ–ї–Њ—Й–∞ –њ–ї–∞—Б—В–Є–љ –Ї–Њ–љ–і–µ–љ—Б–∞—В–Њ—А–∞, d вАУ –≤—Ц–і—Б—В–∞–љ—М –Љ—Ц–ґ –њ–ї–∞—Б—В–Є–љ–∞–Љ–Є.
–†–∞–і—Ц–∞–ї—М–љ–Њ-—Ж–Є–ї—Ц–љ–і—А–Є—З–љ–µ –њ–Њ–ї–µ. –Х–Ї–≤—Ц–њ–Њ—В–µ–љ—Ж—Ц–∞–ї—М–љ–Є–Љ–Є –≤ —Ж—М–Њ–Љ—Г –њ–Њ–ї—Ц —Ф –Ї–Њ–∞–Ї—Б—Ц–∞–ї—М–љ—Ц (, —Й–Њ –Љ–∞—О—В—М –Ј–∞–≥–∞–ї—М–љ—Г –≤—Ц—Б—М) —Ж–Є–ї—Ц–љ–і—А–Є—З–љ—Ц –њ–Њ–≤–µ—А—Е–љ—Ц, –∞ –ї—Ц–љ—Ц—Ч –Ј—Б—Г–≤–Є —А–Њ–Ј—В–∞—И–Њ–≤—Г—О—В—М—Б—П –≤ —А–∞–і—Ц–∞–ї—М–љ–Њ–Љ—Г –љ–∞–њ—А—П–Љ–Ї—Г. –†–Њ–Ј–њ–Њ–і—Ц–ї –љ–∞–њ—А—Г–ґ–µ–љ–Њ—Б—В—Ц –µ–ї–µ–Ї—В—А–Є—З–љ–Њ–≥–Њ –њ–Њ–ї—П
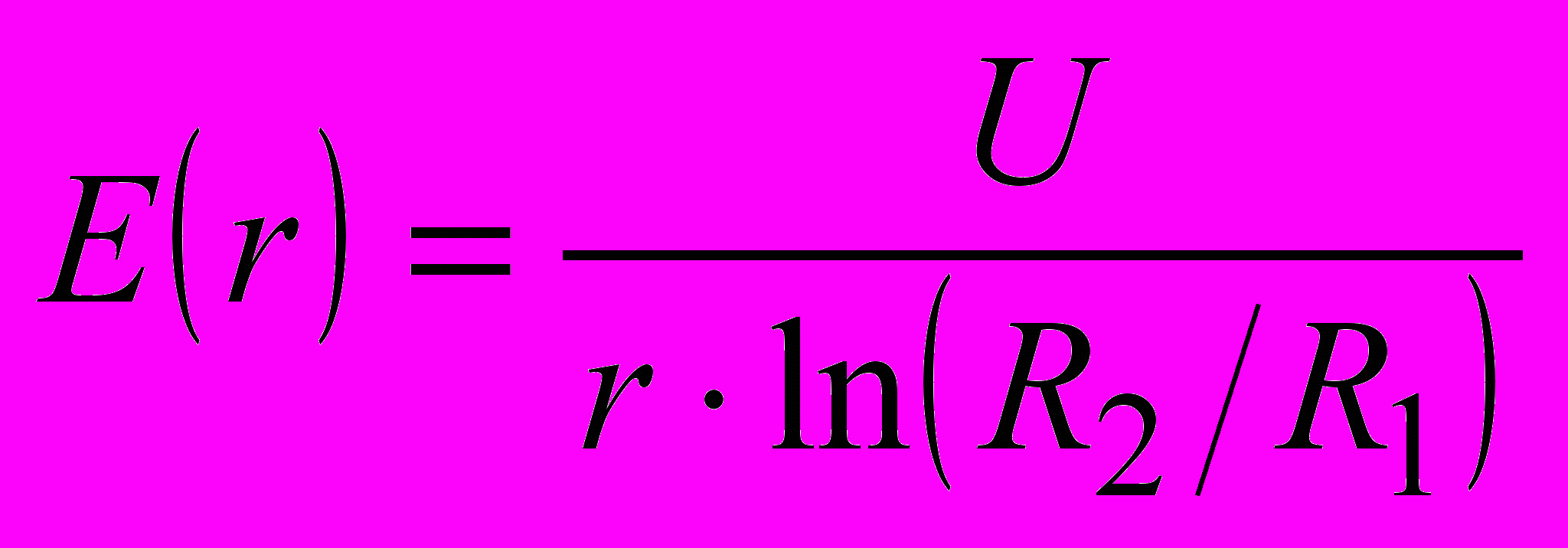 ; —Ф–Љ–љ—Ц—Б—В—М —Ж–Є–ї—Ц–љ–і—А–Є—З–љ–Њ–≥–Њ –Ї–Њ–љ–і–µ–љ—Б–∞—В–Њ—А–∞ (–∞ –і–Њ —В–∞–Ї–Њ—Ч –Ї–Њ–љ—Б—В—А—Г–Ї—Ж—Ц—Ч –Ј–≤–Њ–і–Є—В—М—Б—П –љ–∞–њ—А–Є–Ї–ї–∞–і –Ї–Њ–∞–Ї—Б—Ц–∞–ї—М–љ–Є–є –Ї–∞–±–µ–ї—М)
; —Ф–Љ–љ—Ц—Б—В—М —Ж–Є–ї—Ц–љ–і—А–Є—З–љ–Њ–≥–Њ –Ї–Њ–љ–і–µ–љ—Б–∞—В–Њ—А–∞ (–∞ –і–Њ —В–∞–Ї–Њ—Ч –Ї–Њ–љ—Б—В—А—Г–Ї—Ж—Ц—Ч –Ј–≤–Њ–і–Є—В—М—Б—П –љ–∞–њ—А–Є–Ї–ї–∞–і –Ї–Њ–∞–Ї—Б—Ц–∞–ї—М–љ–Є–є –Ї–∞–±–µ–ї—М) 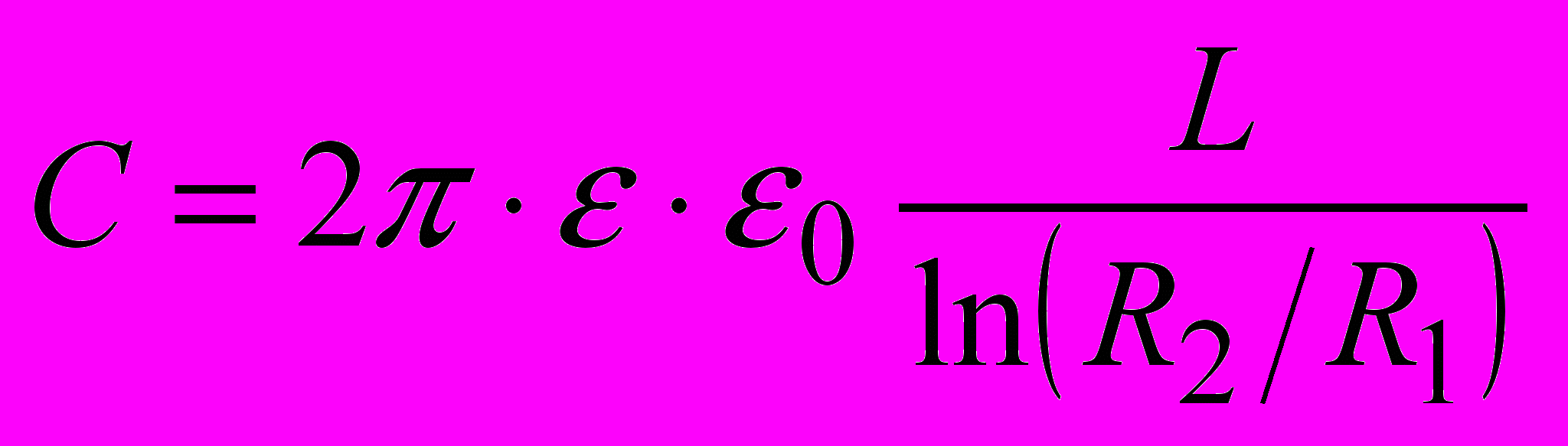 . –Ґ—Г—В ^ L вАУ –і–Њ–≤–ґ–Є–љ–∞ –Ї–Њ–љ–і–µ–љ—Б–∞—В–Њ—А–∞; R2, R1 –≤—Ц–і–њ–Њ–≤—Ц–і–љ–Њ –і—Ц–∞–Љ–µ—В—А–Є –Ј–Њ–≤–љ—Ц—И–љ—М–Њ–≥–Њ –є –≤–љ—Г—В—А—Ц—И–љ—М–Њ–≥–Њ —Ж–Є–ї—Ц–љ–і—А—Ц–≤.
. –Ґ—Г—В ^ L вАУ –і–Њ–≤–ґ–Є–љ–∞ –Ї–Њ–љ–і–µ–љ—Б–∞—В–Њ—А–∞; R2, R1 –≤—Ц–і–њ–Њ–≤—Ц–і–љ–Њ –і—Ц–∞–Љ–µ—В—А–Є –Ј–Њ–≤–љ—Ц—И–љ—М–Њ–≥–Њ –є –≤–љ—Г—В—А—Ц—И–љ—М–Њ–≥–Њ —Ж–Є–ї—Ц–љ–і—А—Ц–≤.