Кулько Тетяна Володимирівна, асистент кафедри
| Вид материала | Документы |
- Навчально-методичний комплекс львів 2009 Бланк Робочої програми навчальної дисицпліни, 273.46kb.
- Освітньо-професійна програма підготовки молодшого спеціаліста (назва освітньо-кваліфікаційного, 1139.28kb.
- Київський національний університет внутрішніх справ На правах рукопису Михальчук Тетяна, 894.19kb.
- Сеник Олеся Ярославівна, асистент Осідач Настасія Богданівна Результати навчання, 16.16kb.
- Ий курс Групи (оа-81, ф-81, е-81) викладач гончаренко тетяна володимирівна вид заняття, 168.8kb.
- Мендрул О. Г., д е. н., професор двнз «енеу ім. В. Гетьмана», Україна Домашенко Тетяна, 110.16kb.
- Навчально-методичний комплекс для студентів юридичного факультету денної форми навчання, 276.78kb.
- Міністерство аграрної політики україни, 584.96kb.
- Е-мережне моделювання процесів системи управління якістю завідувач кафедри ікс,, 34.89kb.
- О. О. Богомольця ковальчук олександр іванович асистент кафедри анатомії людини реферат, 199.19kb.
Міністерство науки i освіти, молоді та спорту України
ЧЕРНІГІВСЬКИЙ ДЕРЖАВНИЙ ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ
МАТЕМАТИЧНІ ЗАДАЧІ ЕЛЕКТРОЕНЕРГЕТИКИ
МЕТОДИЧНІ ВКАЗІВКИ
до виконання лабораторних робіт для студентів за напрямом підготовки
6.050701 “Електротехніка та електротехнології”
Обговорено і рекомендовано
на засіданні кафедри
електричних систем і мереж.
Протокол № 10
від 24 червня 2011р.
Чернігів 2011
Математичні задачі електроенергетики. Методичні вказівки до виконання лабораторних робіт для студентів за напрямом підготовки 6.050701 “Електротехніка та електротехнології”. – Чернігів: ЧДТУ, 2011. – 17 с.
Укладачі: Скоробогатова Валентина Іванівна, завідувач кафедри електричних систем і мереж, доктор технічних наук, професор
Кулько Тетяна Володимирівна, асистент кафедри
електричних систем і мереж
Відповідальний Скоробогатова Валентина Іванівна, завідувач кафедри
за випуск: електричних систем і мереж, доктор технічних наук,
професор
Рецензент: Руновська Людмила Анатоліївна, старший викладач кафедри вищої та прикладної математики Чернігівського державного технологічного університету
ЗМІСТ
| ВСТУП….................................................................................................... | 4 |
| 1 СТИСЛІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЛАБОРАТОРНИХ РОБІТ ……................................................................................................. | 5 |
| 2 ТЕМИ ЛАБОРАТОРНИХ РОБІТ ТА ЗАВДАННЯ ДО НИХ....... | 9 |
| 3 КОНТРОЛЬНІ ЗАПИТАННЯ……………………………………… | 15 |
| Додаток А Перелік основних функцій системи Maple, що використовуються при виконанні лабораторних робіт…………... | 16 |
| РЕКОМЕНДОВАНА ЛІТЕРАТУРА.................................................... | 17 |
В
СТУП Методичні вказівки до виконання лабораторних робіт призначені для покращення засвоєння студентами матеріалу дисципліни «Математичні задачі електроенергетики» шляхом набуття практичних навичок застосування знань для розрахунків усталених режимів роботи електричних систем при виконанні лабораторних робіт. Під час лабораторних занять студенти проводять математичне моделювання усталених режимів роботи електричних систем. Моделювання проводиться на ПК з використанням системи комп’ютерної алгебри Maple. Методичні вказівки складаються зі стислих теоретичних відомостей, тем лабораторних робіт та завдання до них, контрольних запитань. Стислі теоретичні відомості містять посилання на відповідні джерела рекомендованої літератури, за якими студент може більш детально ознайомитися з матеріалом, що використовується при виконанні відповідної лабораторної роботи. Завдання до лабораторних робіт представлені у вигляді схем електричних систем, їх параметрів та вихідних параметрів усталеного режиму роботи системи. Завдання спрямовані на закріплення вивченого теоретичного матеріалу та набуття практичних навичок його застосування при розрахунках усталених режимів роботи електроенергетичних систем.
1 СТИСЛІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЛАБОРАТОРНИХ РОБІТ
Електрична система є сукупністю паралельно працюючих електростанцій, електричних мереж та споживачів електричної енергії, зв'язаних єдністю процесів виробництва, передачі, розподілу та споживання електричної енергії, при загальному централізованому оперативному управлінні.
Стан електричної системи у будь-який момент часу, що визначається значеннями потужності, напруги, струму, частоти, називається режимом, а перераховані величини - параметрами режиму.
Щоб виконати математичний опис електричної системи, треба представити у вигляді математичної моделі зв'язки між параметрами режиму. Розрізняють три види режимів: нормальний усталений, післяаварійний усталений, перехідний. Зв'язки між параметрами перших двох режимів описуються рівняннями алгебри. Перехідні режими описуються диференціальними рівняннями [7, 8, 16, 17].
При вивченні цієї теми необхідно засвоїти, як складаються схема заміщення електричної системи, схеми заміщення ліній і трансформаторів для розрахунків усталених режимів, а також одержати уявлення про моделі джерел активної та реактивної енергії, характеристики навантажень, про способи регулювання напруги та їх урахування при виконанні розрахунків усталених режимів електроенергетичних систем.
У комплексі досліджень умов роботи електричних систем основну частку складають розрахунки усталених режимів. Вони представляють безпосередній інтерес для цілей проектування та експлуатації електричних систем, а також використовуються для отримання початкових даних при дослідженні перехідних режимів, струмів короткого замикання, статичної та динамічної стійкості системи, оптимізації поточних та перспективних режимів.
Стан електричного кола описується рівняннями за законами Ома та Кірхгофа. Число незалежних рівнянь визначається кількістю вузлів та віток схеми заміщення. Процедура формування рівнянь стану для складних схем довільної конфігурації формалізується на основі аналітичного представлення конфігурації схеми заміщення за допомогою графів та матриць. Параметри режиму електричної системи представляються матрицями-стовпцями, а параметри схеми заміщення - квадратними матрицями. Застосування матриць вимагає нумерації віток та вузлів схеми заміщення, а також розташування елементів матриць у порядку зростання їх індексів. Направлений граф схеми можна описати аналітично матрицею з'єднань у вузлах та матрицею з'єднань в незалежні контури [8, 16, 17].
За допомогою матриць з'єднань рівняння стану електричного ланцюга записуються в узагальненій формі, справедливій для схеми будь-якої конфігурації. Із законів Ома та Кірхгофа витікає метод формування математичних моделей усталеного режиму - метод вузлових напруг, який є основним методом, що використовується для складання системи рівнянь усталеного режиму. Щоб одержати цю систему, достатньо для кожного з вузлів електричної системи записати рівняння першого закону Кірхгофа, а потім струми віток замінити через напруги прилеглих вузлів, скориставшись для цього законом Ома. Виведення узагальнених вузлових рівнянь в матричній формі надано в [4, 14, 16].
Рівняння вузлових напруг в матричній формі має вигляд:
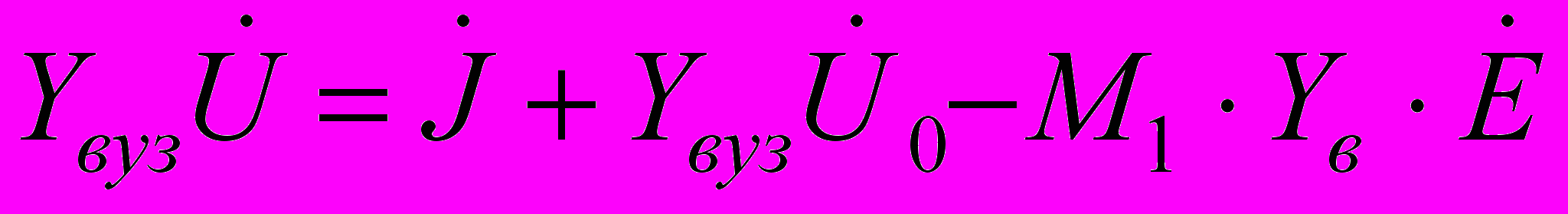, (1.1)де
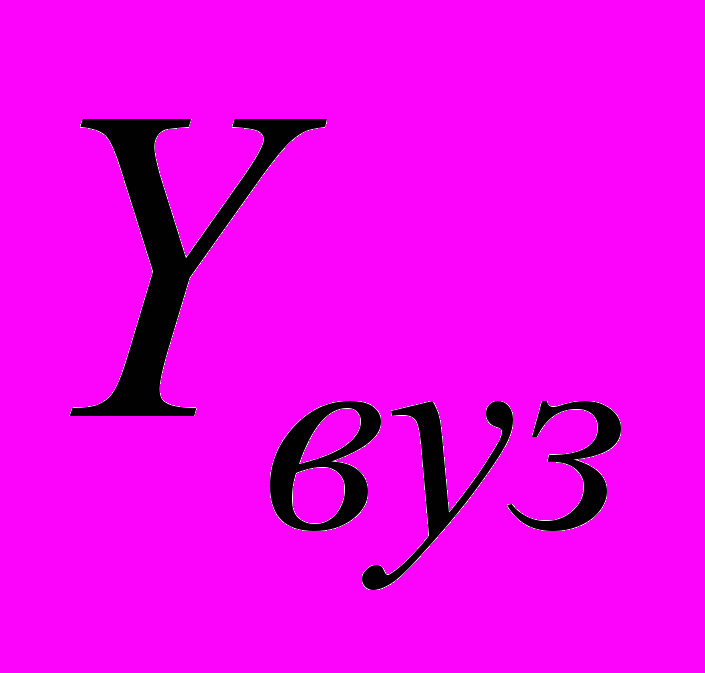- матриця вузлових провідностей; 
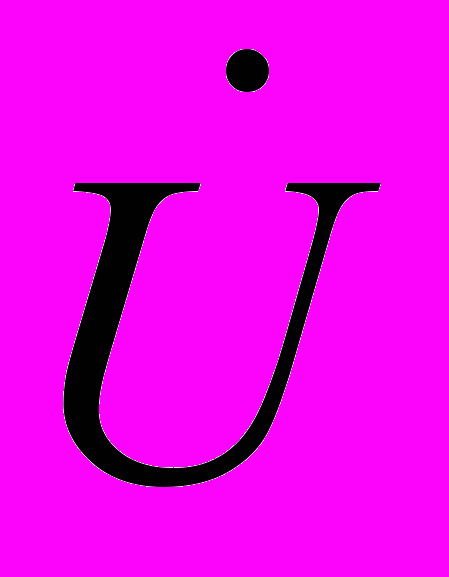- матриця напруг незалежних вузлів; 
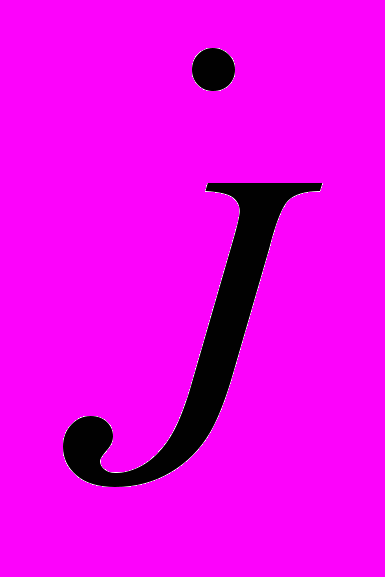- матриця задаючих струмів; 
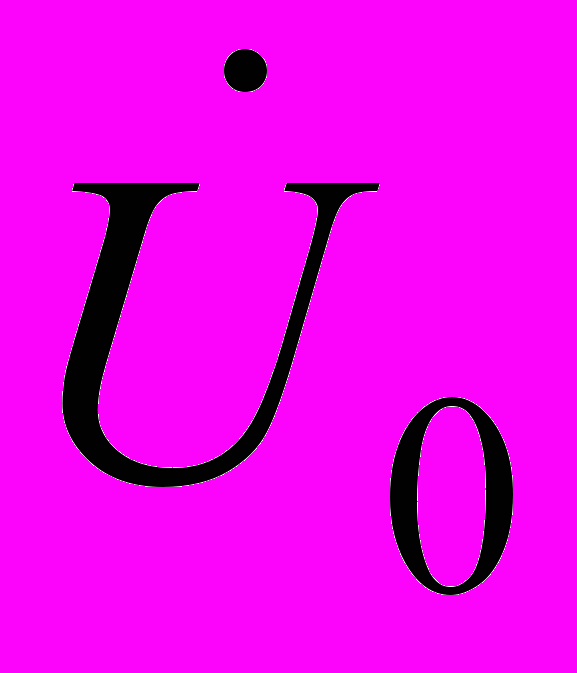- матриця-стовпчик, кожен елемент якої дорівнює напрузі балансуючого вузла; 
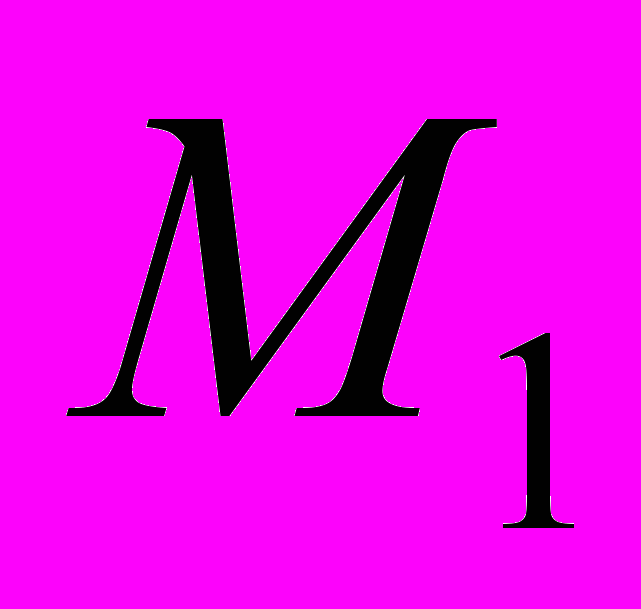- матриця з’єднань у вузлах; 
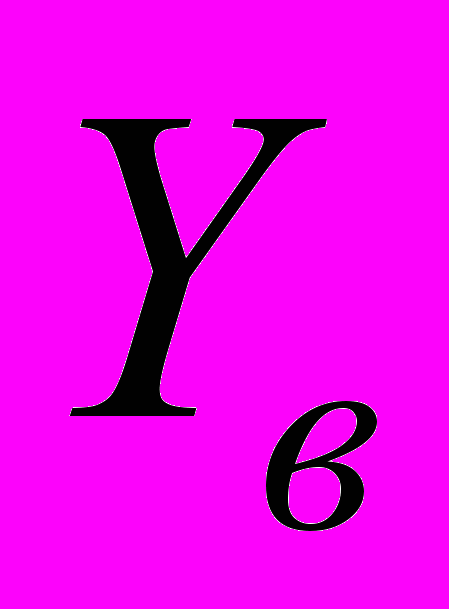- матриця провідностей віток; 
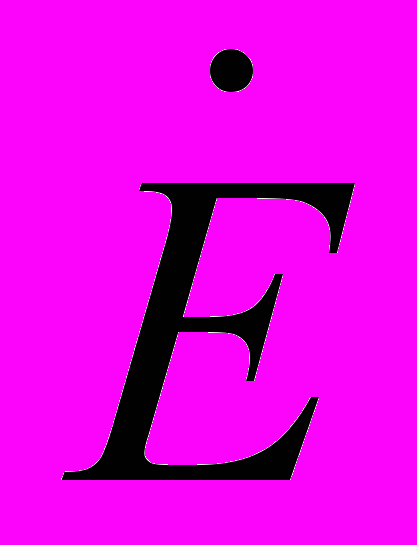- матриця е.р.с. віток. 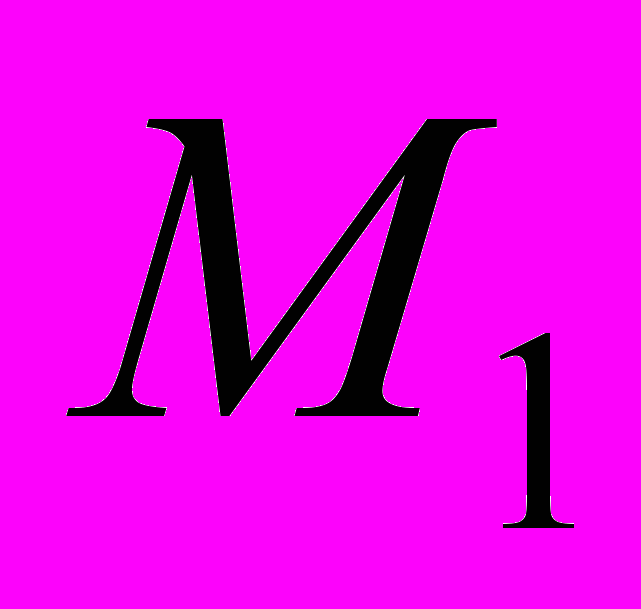складається за направленим графом схеми заміщення. Правило її формування в [1, 11, 13, 15, 16].Кожен елемент матриці
визначається за формулою: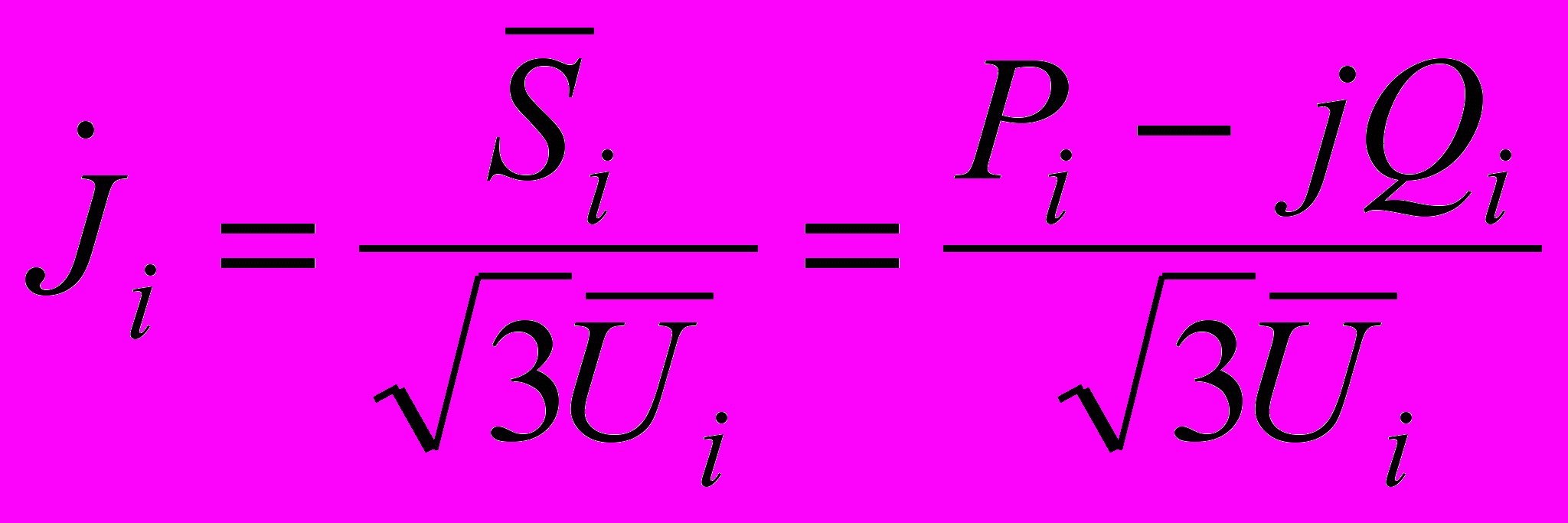
, (1.2)де
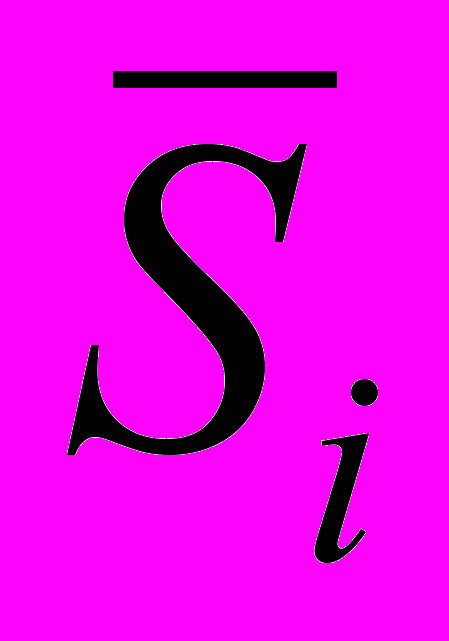- спряжений комплекс трифазної потужності 
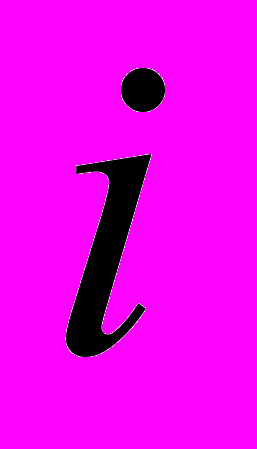-го вузла, МВА; 
- спряжений комплекс лінійної напруги 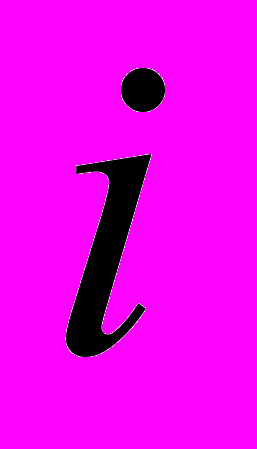-го вузла, кВ.Формування вузлових рівнянь зводиться до визначення матриці вузлових провідностей. Залежно від розрахункових умов вид цієї матриці може бути різним [16].
Після визначення напруг вузлів струми в вітках можуть бути знайдені схеми за виразом
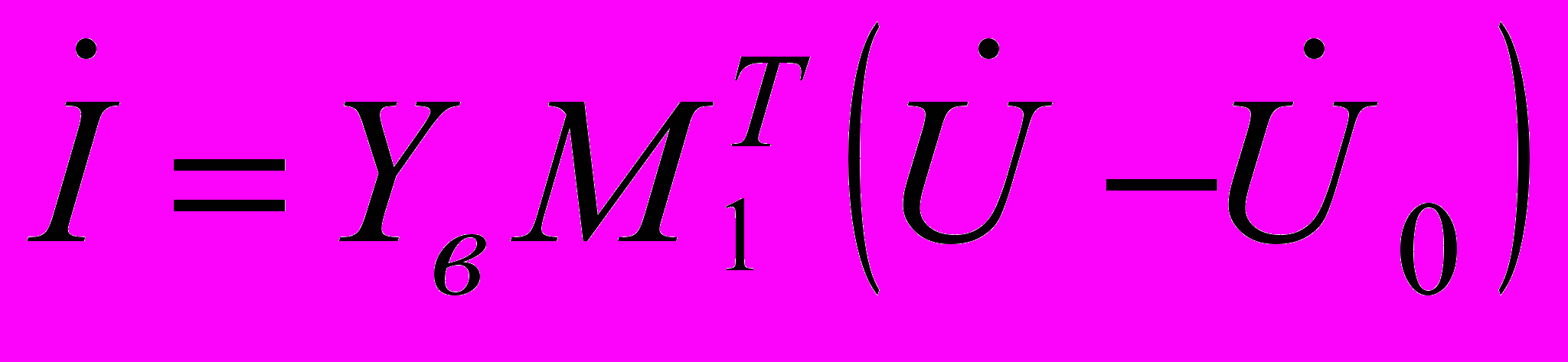, (1.3)де
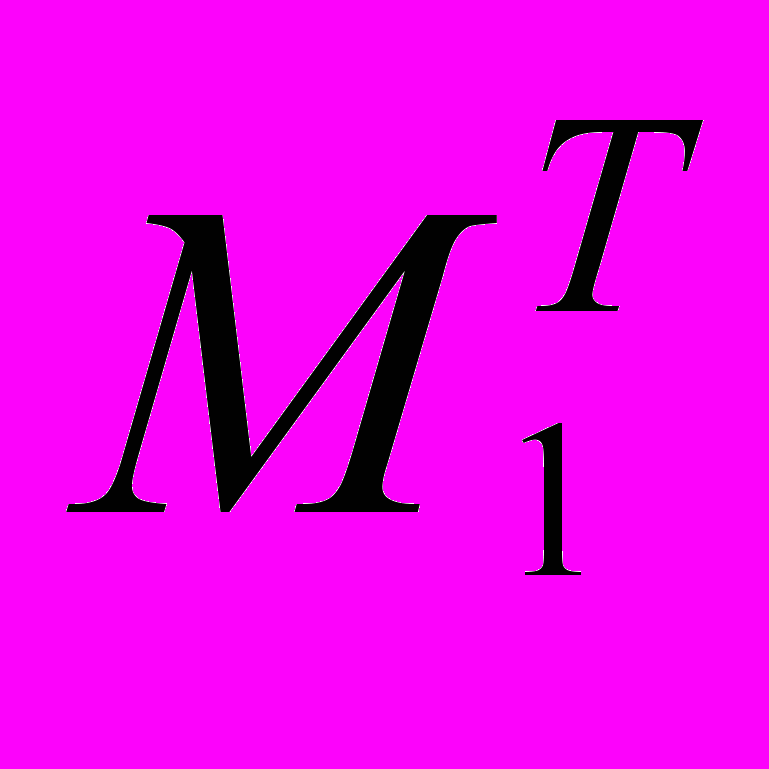- транспонована матриця з’єднань у вузлах.Узагальнене математичне рівняння, яке відображує енергетичний стан будь-якої електричної системи в усталеному режимі, має вигляд:
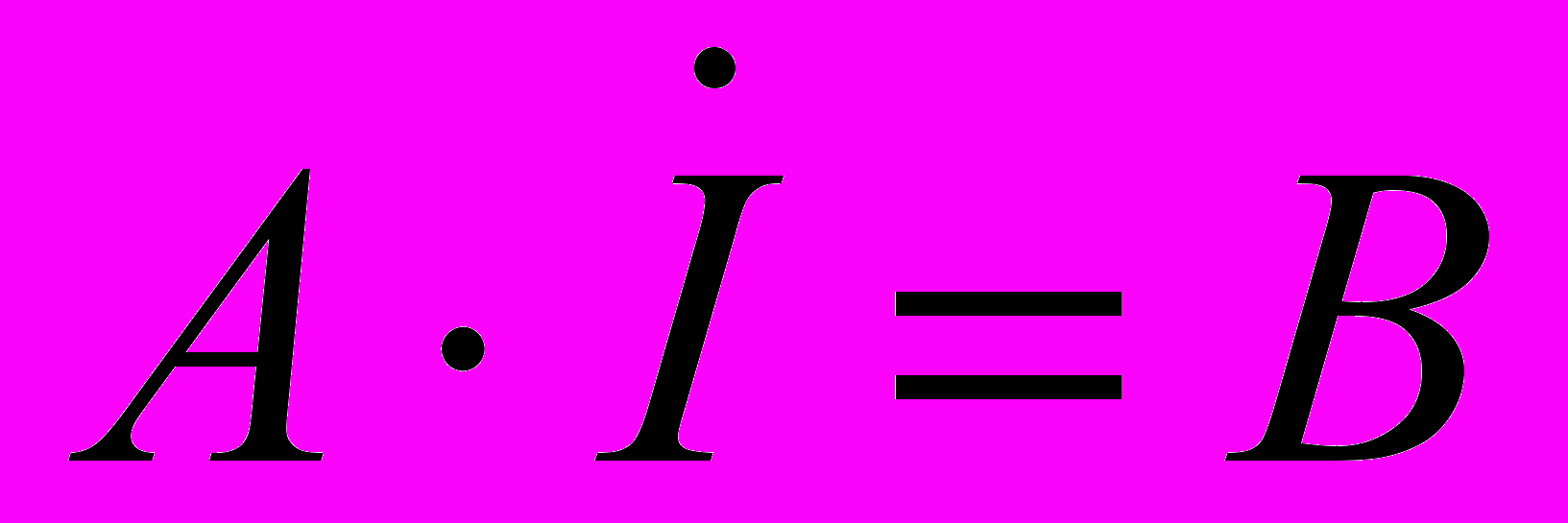. (1.4)або
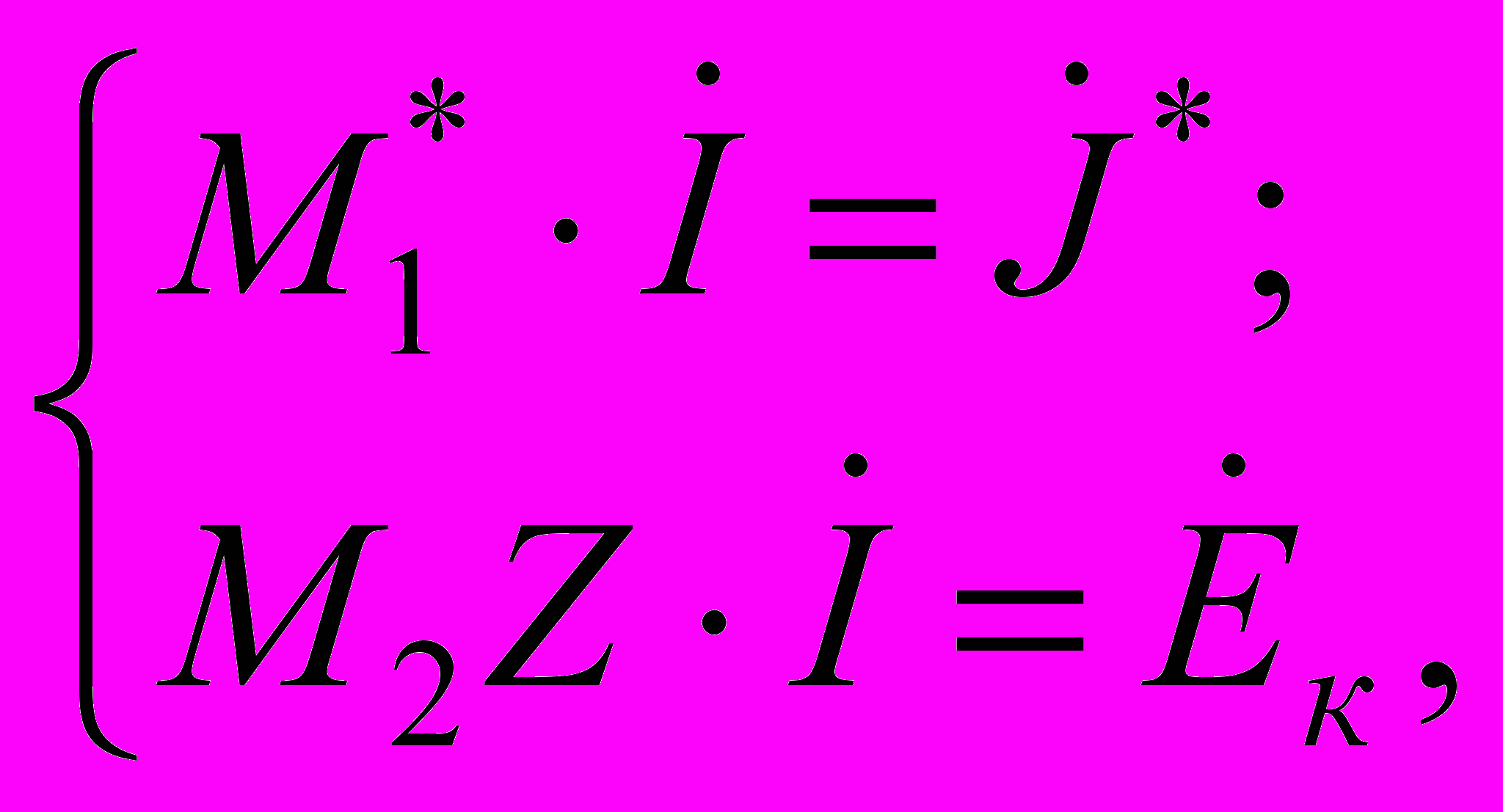(1.5)де
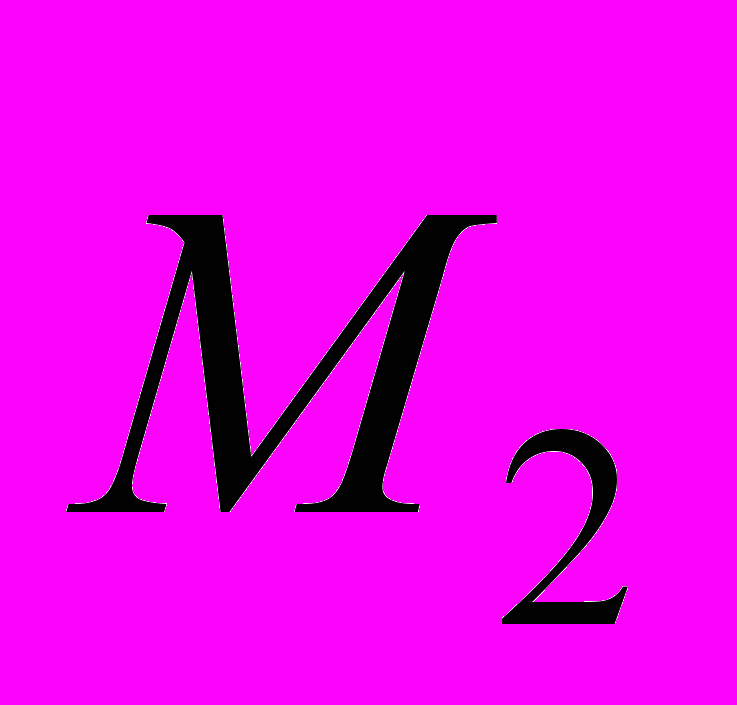- матриця з’єднань в незалежні контури; 
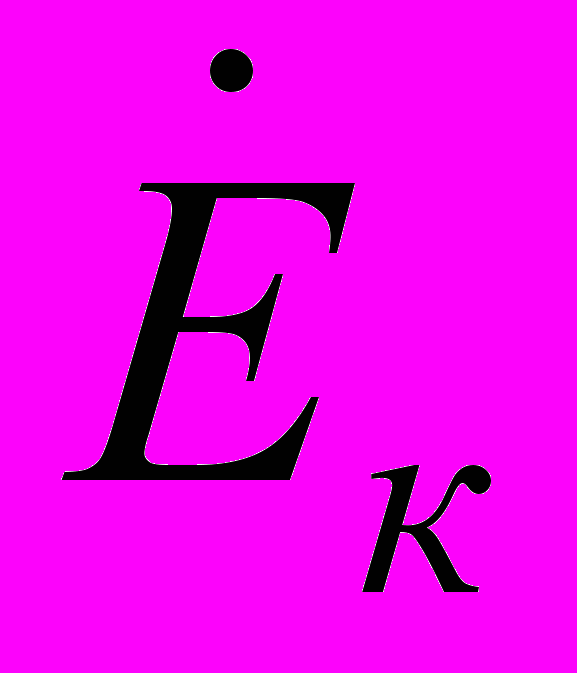- матриця-стовпчик контурних е.р.с.Матриця контурних е.р.с. розраховується за формулою:
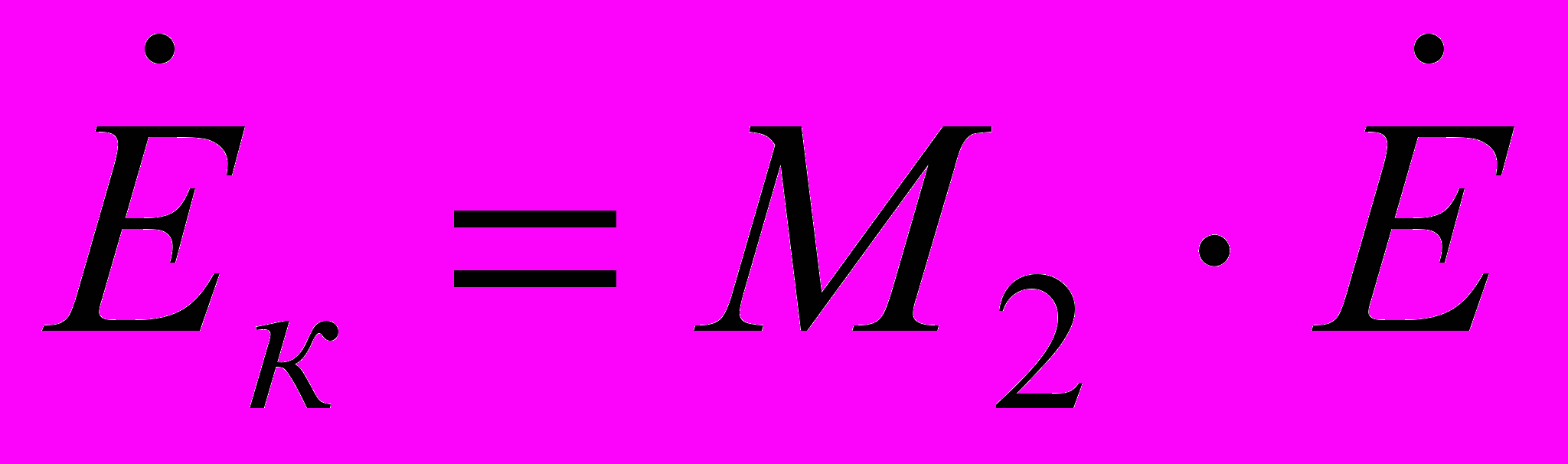.Для розрахунку напруг у вузлах схеми необхідно виділити дерево графа і тоді:
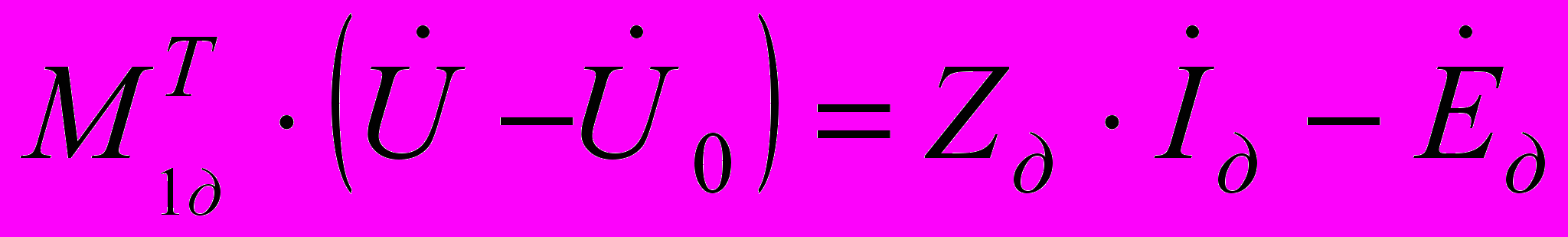. (1.6)З математичної точки зору задача розрахунку усталеного режиму зводиться до рішення системи нелінійних рівнянь, яка може бути вирішена ітераційним методом. При цьому на кожному кроці ітераційного процесу розв'язується лінійна або лінеаризована система цих рівнянь. Методи рішення систем лінійних рівнянь алгебри розділяються на прямі та ітераційні [2, 3].
Точність розв’язку СЛАР залежить від обумовленості матриці коефіцієнтів. Якщо малі збурення коефіцієнтів і (або) вільних членів системи дуже збурюють її розв’язок, то таку систему рівнянь називають погано обумовленою.
Ознакою поганої обумовленості СЛАР є її майже виродженість. Якщо значення визначника системи досить мале порівняно з її коефіцієнтами, то така системи близька до виродженої. Добре обумовленою вважається СЛАР, визначник якої є величиною не нижчого порядку, ніж її коефіцієнти [10].
Оцінити обумовленість матриці коефіцієнтів можна за нерівністю:
, (1.7)де
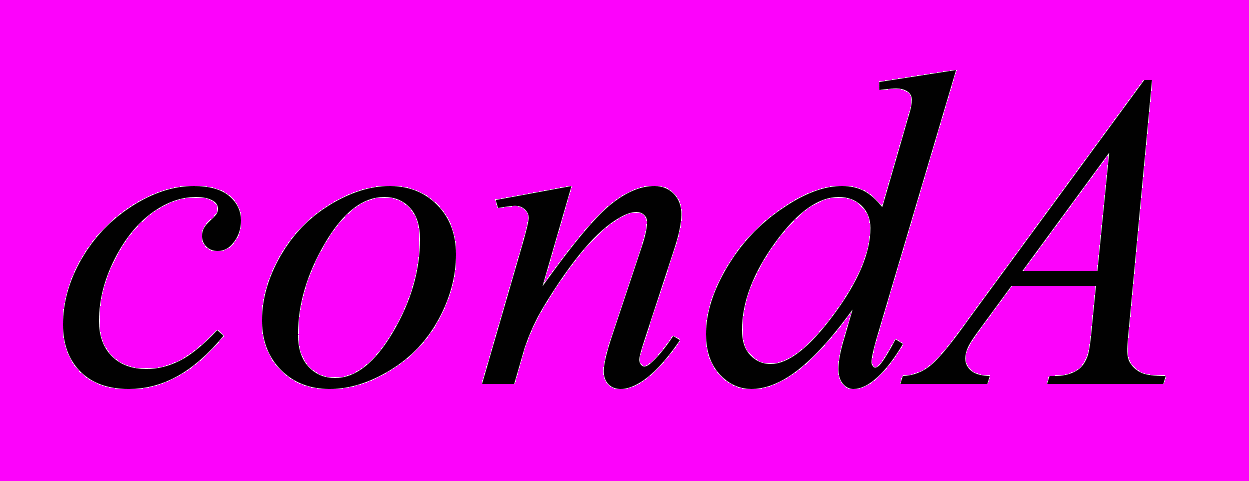- число обумовленості матриці коефіцієнтів;
, 
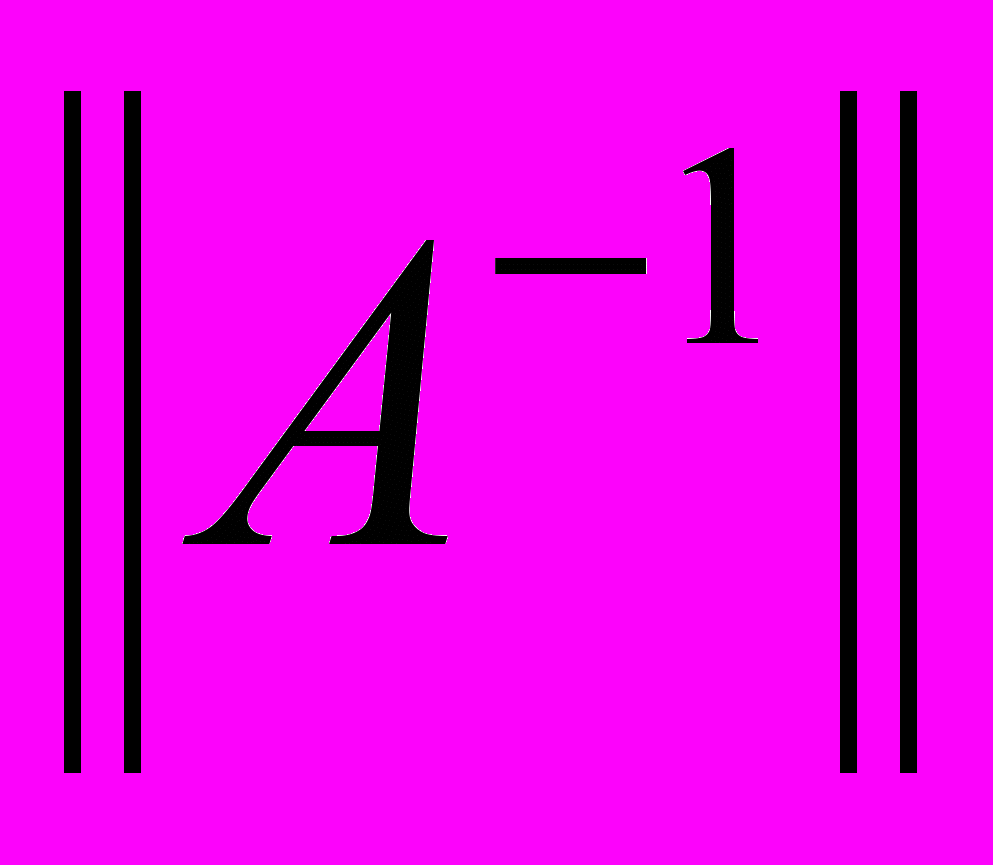- норма матриці коефіцієнтів та оберненої до неї матриці відповідно; 
, 
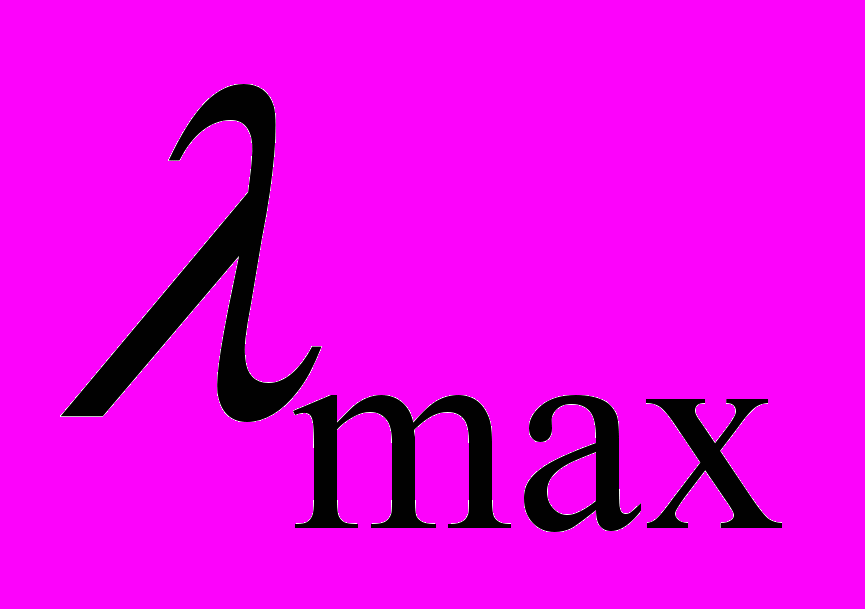- максимальне та мінімальне власне значення матриці коефіцієнтів відповідно.Власні значення матриці є коренями характеристичного рівняння
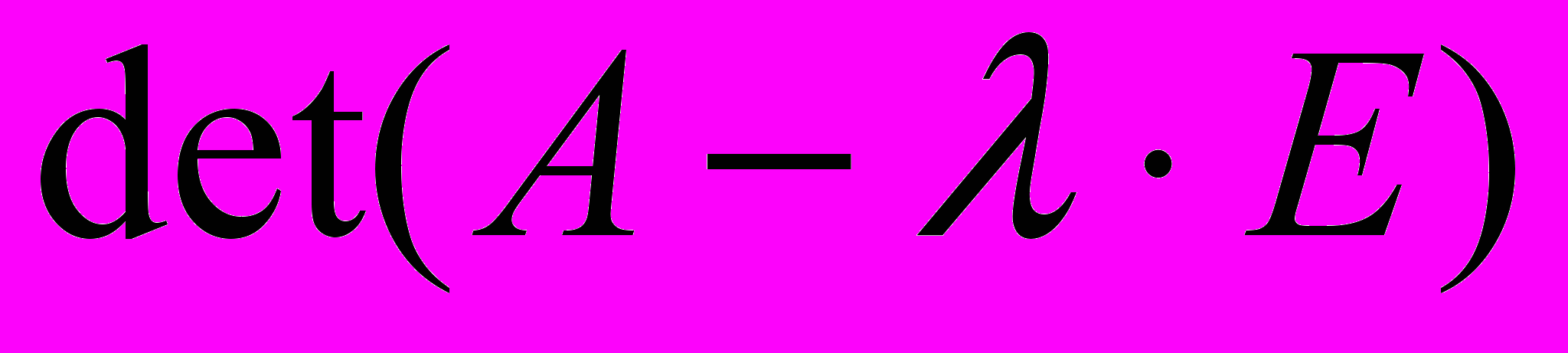. Якщо число 
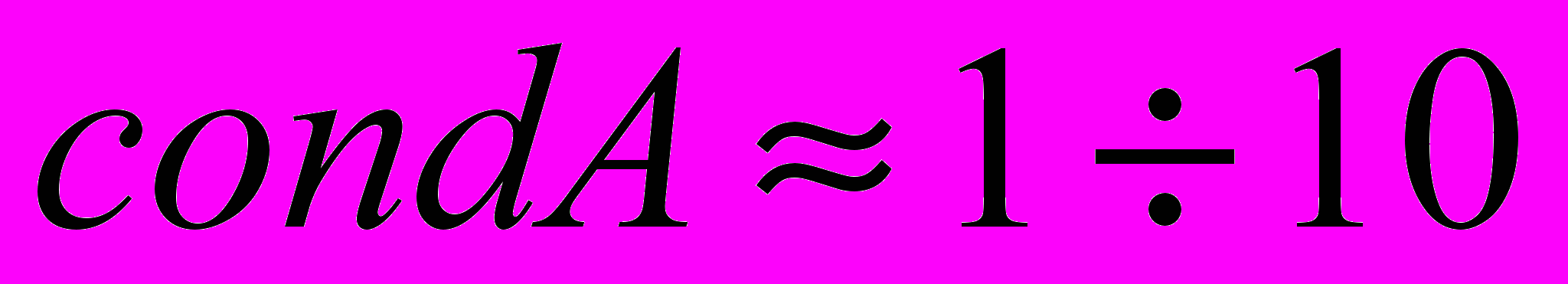, то матриця 
вважається добре обумовленою, якщо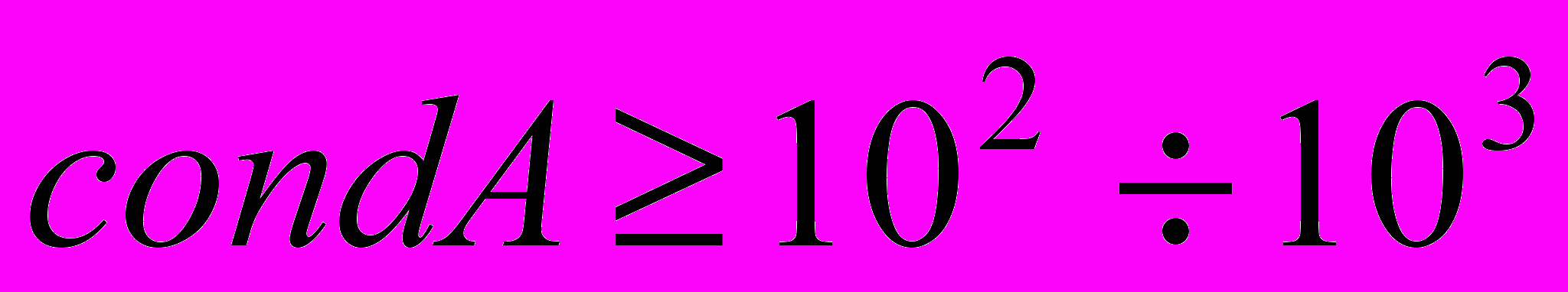 
матриця вважається погано обумовленою та отримане прямими методами рішення СЛАР необхідно уточнювати [5]. Ознакою закінчення ітераційного процесу є виконання умови
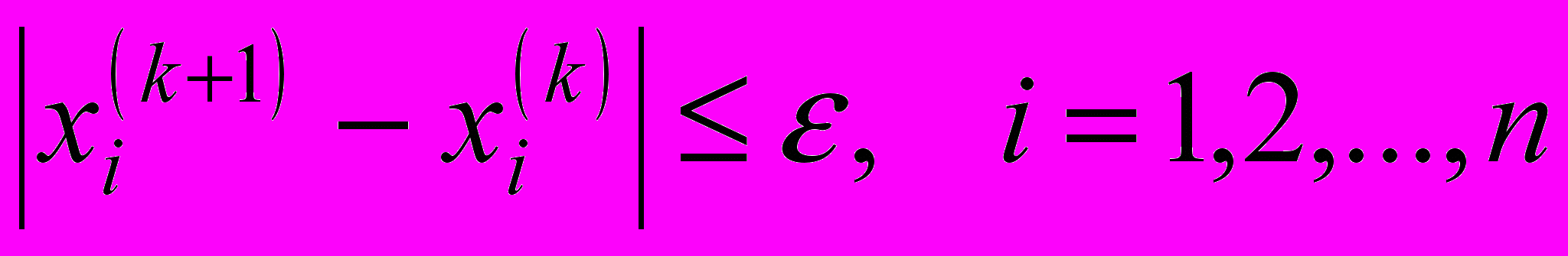, (1.8)де
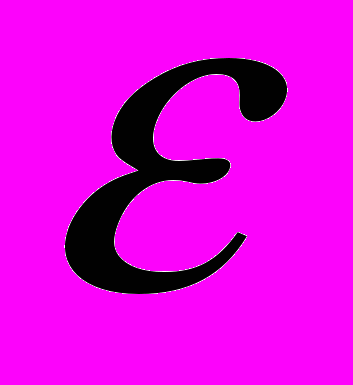– точність, обумовлена фізичними та технічними факторами задачі, що вирішується.Щоб умова (1.8) виконувалась необхідно мати збіжний ітераційний процес. Для оцінки збіжності існують достатні умови, що забезпечують виконання умови збіжності:
,
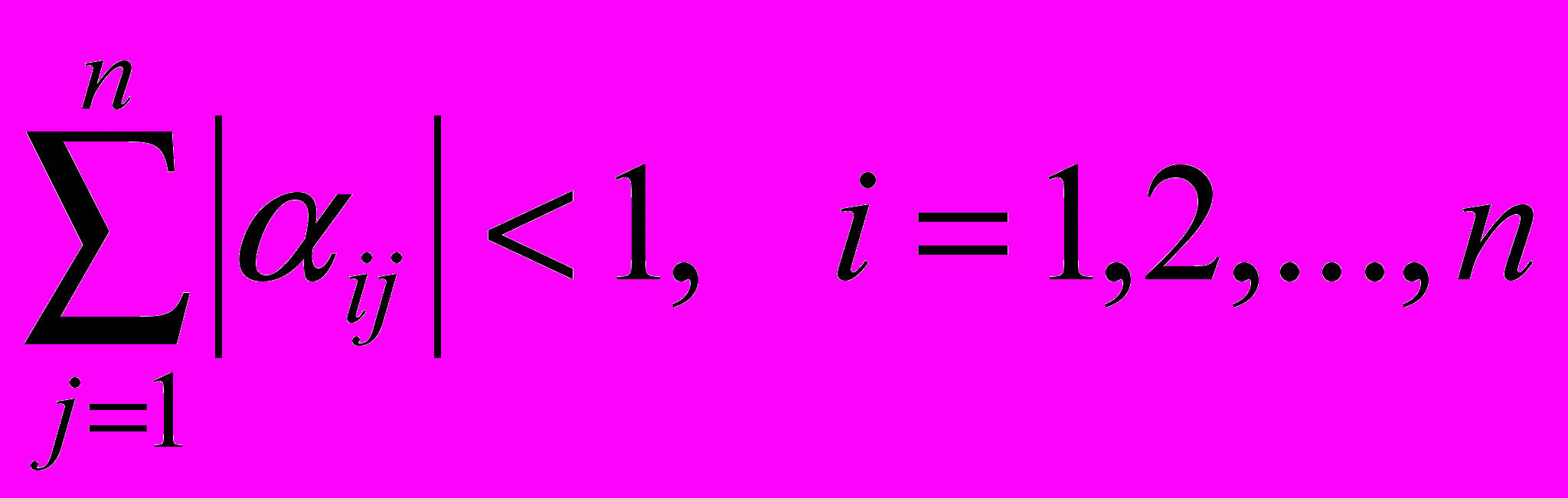,або
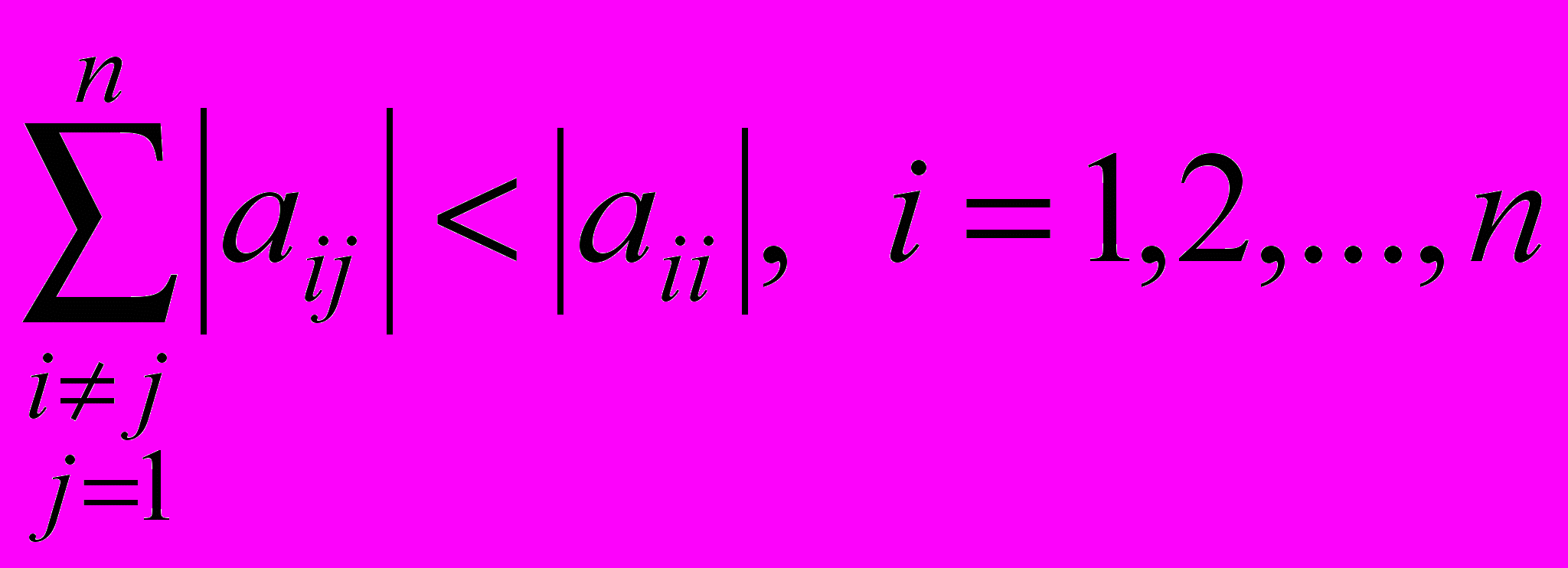.Алгоритм рішення СЛАР методом простої ітерації:
- представляємо кожне
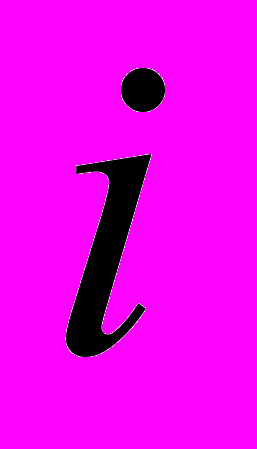-те рівняння у вигляді рішення відносно 
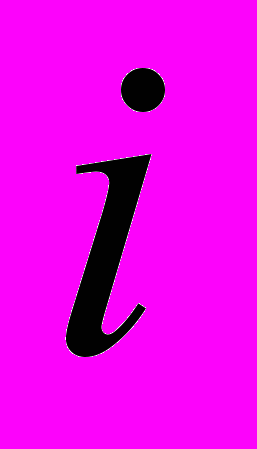-того невідомого;- задаємося нульовими наближеннями, вважаючи їх рішеннями (зазвичай в якості нульового наближення приймають вільні члени);
- підставивши нульові наближення в праву частину рівнянь, отримаємо перше наближення. Таким же чином результат може бути використаний для отримання 2-го, 3-го і т.д. до
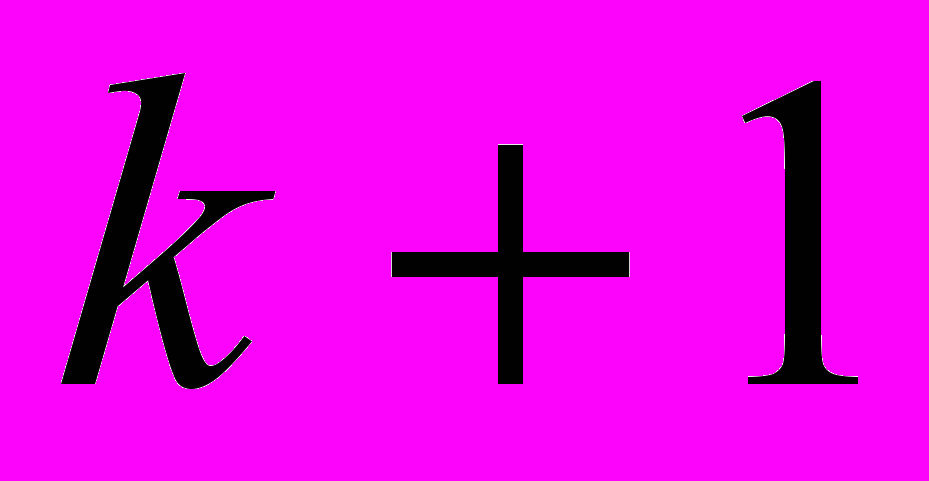-го наближення;- про закінчення процесу свідчить виконання умови (1.8).
2 ТЕМИ ЛАБОРАТОРНИХ РОБІТ ТА ЗАВДАННЯ ДО НИХ
В навчальній програмі дисципліни «Математичні задачі електроенергетики» передбачено виконання циклу лабораторних робіт за наступними темами:
1. Аналіз параметрів нормального усталеного режиму роботи електричної системи.
2. Аналіз параметрів післяаварійного усталеного режиму роботи електричної системи.
Лабораторна робота 1 складається з чотирьох частин, кожна з яких відповідає окремому методу розрахунку параметрів усталеного режиму. Метою лабораторної роботи 1 є моделювання та аналіз параметрів нормального усталеного режиму роботи електричної системи з використанням узагальненого рівняння стану, вузлового рівняння при заданих задаючих струмах та вузлового рівняння при заданих вузлових потужностях, контурного рівняння.
Метою лабораторної роботи 2 є моделювання та аналіз параметрів післяаварійного усталеного режиму роботи електричної системи з використанням вузлового рівняння.
Необхідно визначити залежні параметри нормального усталеного режиму роботи електричної системи, а саме: напругу у вузлах, струми в вітках, втрати активної потужності в елементах системи, а також потужність базисного вузла при заданій напрузі базисного вузла та відомому навантаженні споживачів і генераторів.
Параметри генераторів, ліній, трансформаторів та навантажень споживачів наведені в таблиці 2.1. Позначення наведені на рисунках 2.1-2.10 та в таблиці 2.1: G1, G2, G3 – генератори; Т, Т1, Т2 – трансформатори; АТ – автотрансформатори; Л1, Л2, Л3 – повітряні лінії електропередачі; Р – реактор; СК – синхронний компенсатор; Н1, Н2, Н3 – навантаження споживачів електроенергії.
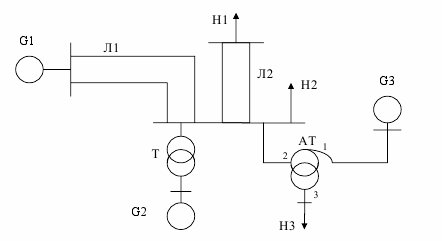
Рисунок 2.1 – Розрахункова схема електричної системи до варіанту 1
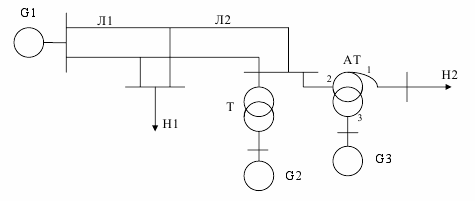
Рисунок 2.2 – Розрахункова схема електричної системи до варіанту 2
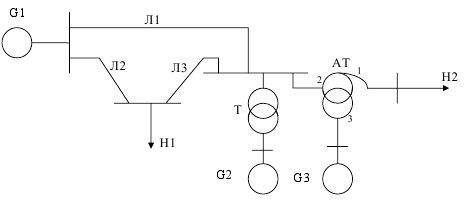
Рисунок 2.3 – Розрахункова схема електричної системи до варіанту 3
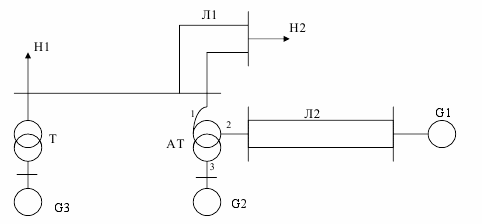
Рисунок 2.4 – Розрахункова схема електричної системи до варіанту 4
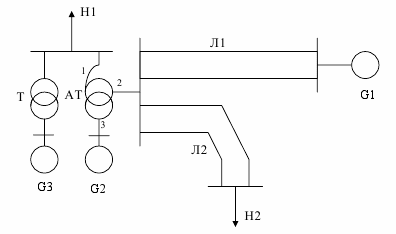
Рисунок 2.5 – Розрахункова схема електричної системи до варіанту 5
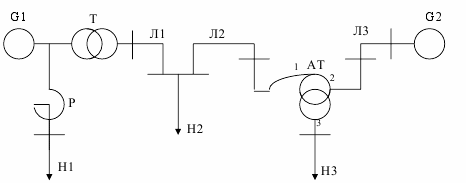
Рисунок 2.6 – Розрахункова схема електричної системи до варіанту 6
Рисунок 2.7 – Розрахункова схема електричної системи до варіанту 7
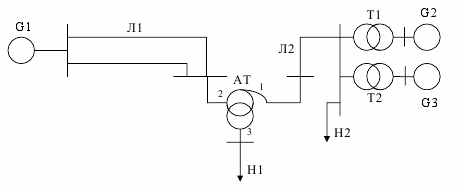
Рисунок 2.8 – Розрахункова схема електричної системи до варіанту 8
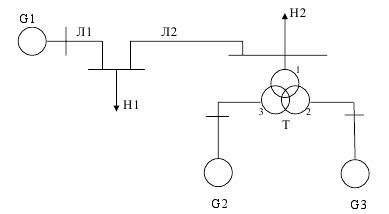
Рисунок 2.9 – Розрахункова схема електричної системи до варіанту 9
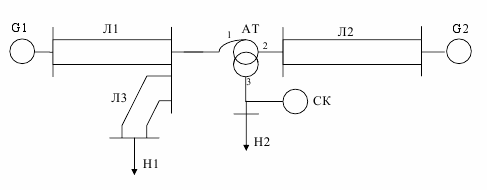
Рисунок 2.10 – Розрахункова схема електричної системи до варіанту 10
Завдання виконується в наступній послідовності. Спочатку складається схема заміщення електричної системи, за якою формується направлений граф, що відображає її структуру.
Систему рівнянь для розрахунку залежних параметрів режиму слід формувати відповідно до мети лабораторної роботи.
Таблиця 2.1 – Варіанти контрольного завдання
| Варіант завдання | Задаючі струми/ потужності | Параметри | |||||||||||||||
| G2 | G3 | H1 | H2 | H3 | СК | Л1 | Л2 | Л3 | Р | Т1 | Т2 | АТ | |||||
| Z | Z | Z | Z | Z1 | Z2 | Z3 | Z | Z1 | Z2 | Z3 | |||||||
| 1 | 0,75+j0,5/ 100+j61 | 0,75+j0,5/ 100+j61 | 0,9+j0,67/ 120+j90 | 0,25+j0,18/ 32+j24 | 0,5+j0,36/70+j54 | – | 23+j6 | 4+j1 | – | – | j14 | – | – | – | j17,4 | 19 | j35 |
| 2 | 0,47+j0,3/ 34+j20 | 0,47+j0,3/ 34+j20 | 0,36+j0,27/ 40+j30 | 0,6+j0,45/ 24+j18 | – | – | 18+j5 | 6+j2 | – | – | j16 | – | – | – | j32 | 25 | j20 |
| 3 | 0,3+j0,25/ 20+j15 | 0,3+j0,25/ 20+j15 | 0,15+j0,12/ 32+j24 | 0,5+j0,18/ 12+j8 | – | – | 44+j11 | 36+j9 | 12+j3,5 | – | j16 | – | – | – | j19 | 15 | j18 |
| 4 | 0,2+j0,1/ 27+j12 | 0,2+j0,1/ 27+j12 | 0,42+j0,36/ 56+j42 | 0,13+j0,11/ 16+j12 | – | – | 12,9+j3 | 19,6+j5 | – | – | j44 | – | – | – | j22 | 34 | j44 |
| 5 | 0,27+j0,17/ 37+j23 | 0,27+j0,17/ 37+j23 | 0,1+j0,15/ 88+j60 | 0,66+j0,45/ 24+j18 | – | – | 21,4+j5,5 | 6,1+j2 | – | – | j35 | – | – | – | j30 | 45 | j60 |
| 6 | 0,24+j0,16/ 29+j21 | – | 0,15+j0,13/ 20+j16 | 0,2+j0,14/ 24+j18 | 0,3+j0,10/30+j15 | – | 16+j4 | 2,4+j6 | 40+j10 | j68 | j44 | – | – | – | j53 | 65 | j105 |
| 7 | 0,3+j0,22/ 40+j30 | – | 0,15+j011/ 20+j15 | 0,66+j0,45/ 24+j18 | – | – | 24+j6 | 1,6+j4 | – | – | j39 | | | | j28 | 44 | j56 |
| 8 | 0,24+j0,16/ 33+j20 | 0,24+j0,16/ 33+j20 | 0,18+j012/ 75+j48 | 0,40+j0,23/ 24+j18 | – | – | 23+j6,5 | 29,5+j7 | – | – | j46,5 | – | – | j46,5 | j34,5 | 22 | j79 |
| 9 | 0,1+j0,08/ 13,6+j10 | 0,1+j0,08/ 13,6+j10 | 0,24+j0,18/ 32+j24 | 0,18+j0,19/ 24+j18 | – | – | 44+j12 | 44+j12 | – | – | j19 | j40 | j40 | – | – | – | – |
| 10 | 0,24+j0,16/ 29+j21 | – | 0,16+j0,12/ 20+j15 | 0,3+j0,25/ 24+j0,18 | – | j0,25/ j33 | 41+j6 | 8+j1 | 20+j3 | – | – | – | – | – | j17 | 25 | j34 |
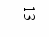
14
Щоб визначити втрати потужності та потужність базисного вузла, доцільно сформувати матрицю повної потужності в вітках схеми
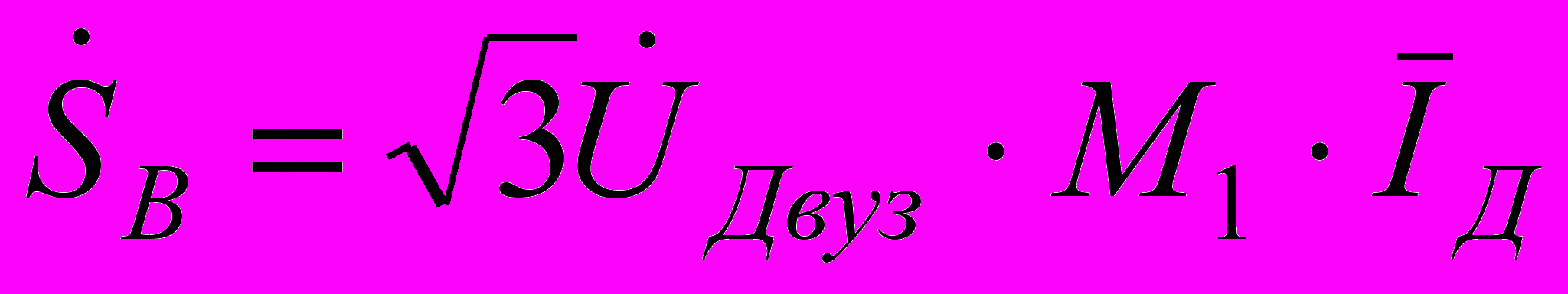, (2.1)де
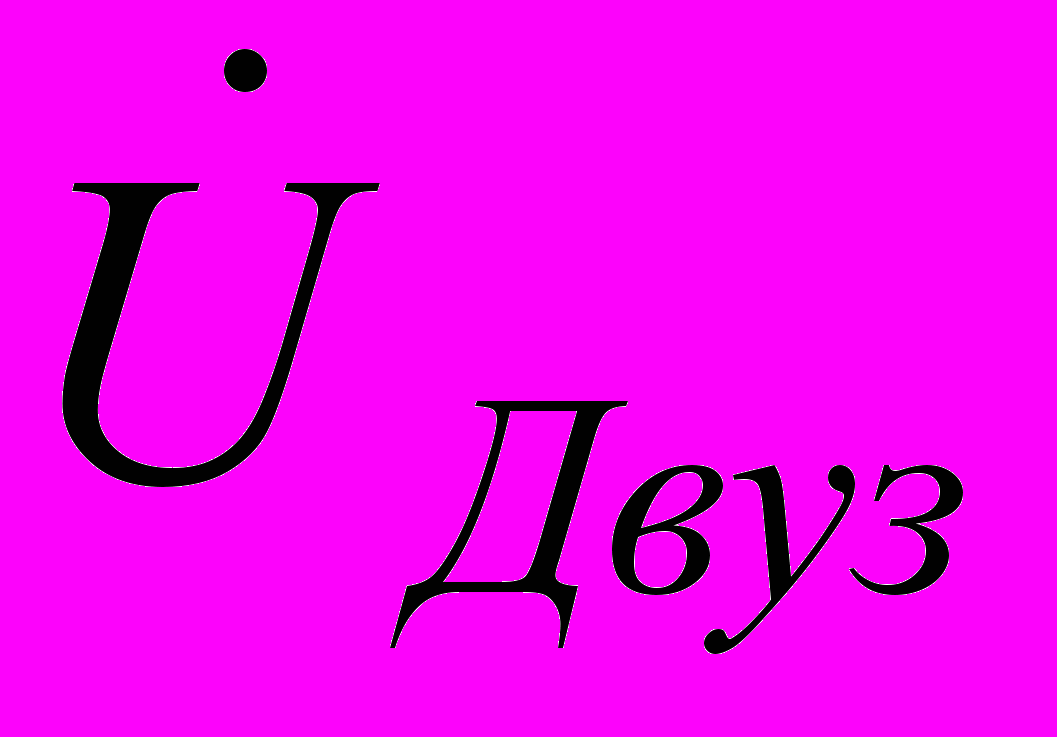- діагональна матриця напруг вузлів; 
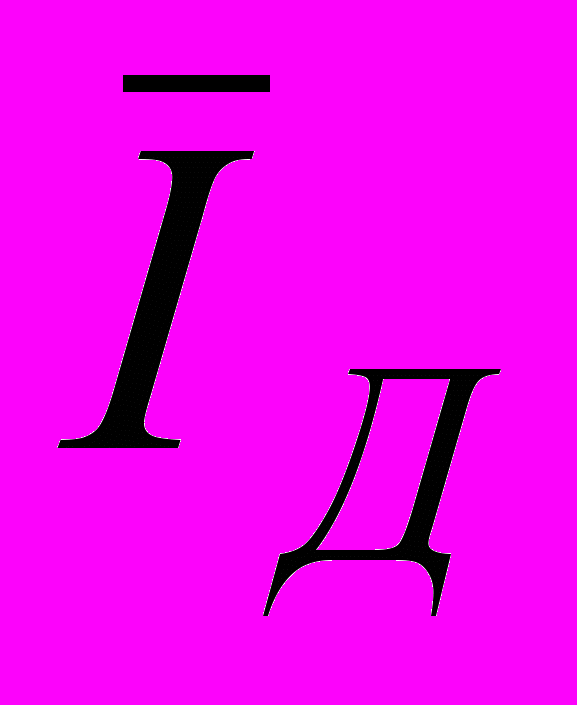- діагональна матриця спряжених комплексів струму віток.Матриця
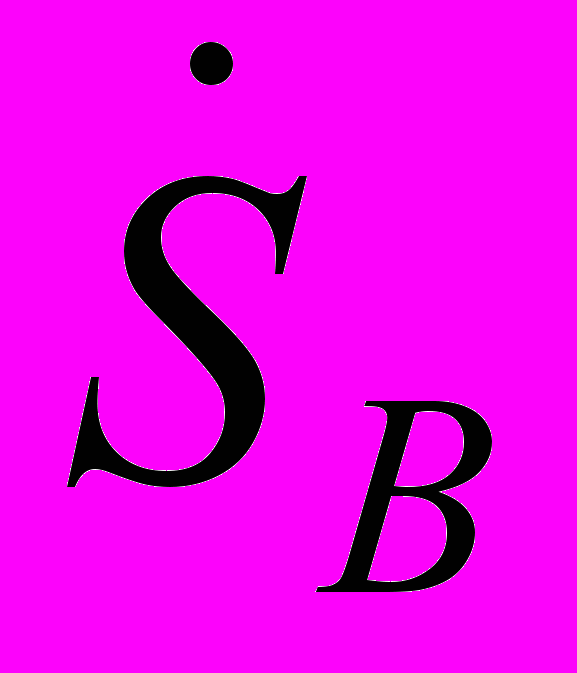прямокутна з числом рядків, що відповідає кількості вузлів, та числом стовпчиків, що дорівнює кількості віток схеми. Матриця містить значення повної потужності на початку та в кінці кожної вітки. При цьому позитивною виходить потужність передачі до вузла, а від’ємною – від вузла. Сума значень, розташованих в кожному рядку 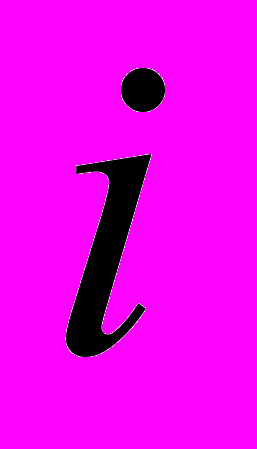матриці дає повну потужність, що обумовлена задаючим струмом у вузлі 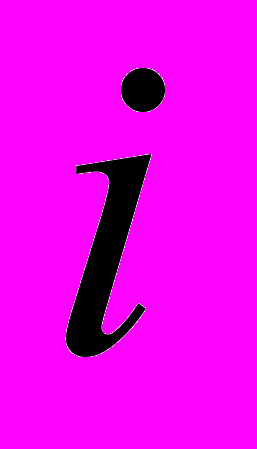. Потужність базисного вузла визначається як сума елементів останнього рядка. Сума значень, розташованих в кожному стовпчику 
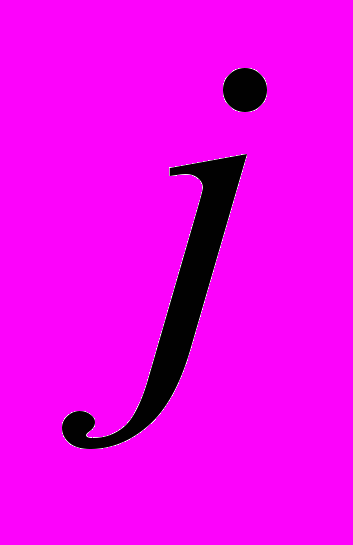матриці дає повні втрати потужності у вітці 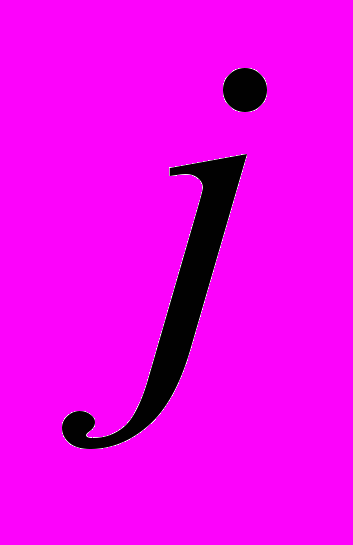.Звіт з лабораторної роботи повинен містити її назву, мету, розрахункову схему електричної системи (згідно варіанту), схему заміщення електричної системи, алгоритм розрахунку залежних параметрів режиму та робочий документ Maple з детальними коментарями, який має містити граф, що відображає структуру електричної системи, та розраховані залежні параметри режиму роботи електричної системи. У висновку до лабораторної роботи необхідно навести результати аналізу залежних параметрів режиму та запропонувати заходи підвищення ефективності роботи електричної системи.
В додатку А наведені основні команди та функції системи Maple, що використовуються для побудови графів та при розрахунку параметрів режиму роботи електричної системи.
3 КОНТРОЛЬНІ ЗАПИТАННЯ
- Що розуміють під електричною системою?
- Що розуміють під режимом електричної системи, які величини називають його параметрами?
- Назвіть види режимів електричної системи. Надайте їм характеристику.
- Які схеми заміщення застосовуються для ліній електропередачі?
- Які схеми заміщення застосовуються для трансформаторів та автотрансформаторів?
- Як задають навантаження генераторів та споживачів при розрахунках усталеного режиму?
- Як скласти схему заміщення електричної системи?
- При яких припущеннях схема заміщення електричної системи представляє лінійне електричне коло?
- Дайте поняття балансуючого вузла.
- Назвіть правила формування матриць з'єднання віток у вузлах та в незалежні контури.
- Запишіть в матричній формі рівняння законів Ома та Кірхгофа.
- Покажіть, як за допомогою законів Ома та Кірхгофа одержати вузлове рівняння у формі, що використовує матрицю вузлових провідностей.
- Напишіть вираз, за допомогою якого формується матриця вузлових провідностей.
- Назвіть властивості матриці вузлових провідностей при поєднанні балансуючого по струму та базисного по напрузі вузлів.
- Як визначити матрицю вузлових опорів?
- Як з системи лінійних рівнянь вузлових напруг, записаних з використанням матриці вузлових провідностей, одержати рівняння з матрицею вузлових опорів?
- Для вирішення яких задач потрібне виконання розрахунків усталеного режиму електричної системи?
- Викладіть обчислювальні алгоритми методу Гауса із зворотним ходом та без зворотного ходу.
- Викладіть обчислювальний алгоритм методу простої ітерації.
- У чому особливість методу Зейделя в порівнянні з методом простої ітерації?
- Як з нелінійних рівнянь вузлових напруг у формі балансу вузлових струмів одержати рівняння у формі балансу потужностей?
- Як визначити струми у вітках, потоки та втрати потужності в електричній системі?
- Що таке збіжність ітераційного процесу?
Додаток А
Перелік основних функцій системи Maple, що використовуються при виконанні лабораторних робіт
Команда запуску пакету функцій теорії графів – with(networks);
функція створення пустого графу – new();
функція створення пустого графу (без ребер) – void();
функція побудови креслення графу – draw();
функція додавання до графу ребер – addedge();
функція видалення з графу ребер або вершин – delete();
функція з’єднання одних заданих вершин з іншими – connect();
функція розрахунку першої матриці інциденцій – incidence();
команда запуску пакету функцій лінійної алгебри – with(linalg);
функція створення матриці – Matrix ();
функція створення діагональної матриці – diag();
функція видалення рядків матриці – delrows ();
функція добутку матриць А та В – multiply(A,B) або evalm(A&*B);
функція суми матриць А та В – matadd(A,B) або evalm(A+B);
функція розрахунку визначника матриці – det();
функція розрахунку числа обумовленості матриці – cond();
функція розрахунку оберненої матриці – inverse();
функція рішення лінійних рівнянь – linsolve ();
функція вертикального злиття двох матриць – stack();
функція горизонтального злиття двох матриць – concat();
функція перетворення Гауса-Жордана матриці – gaussjord() або rref();
функція отримує вказану підматрицю з матриці – submatrix().
З деталями синтаксису для кожної з вказаних функцій можна ознайомитися в довідковій системі Maple. Для цього достатньо використати команду ?name;, де name – ім’я функції, або навести курсор на ім’я функції та натиснути клавішу F1.
РЕКОМЕНДОВАНА ЛІТЕРАТУРА
- Астраханов Ю.А., Веников В.А., Ежков В.В. Электроэнергетические системы в примерах и иллюстрациях. – М.: Высшая школа, 1989.
- Беллман Р. Введение в теорию матриц. – М.: Наука, 1969. – 368 с.
- Вержбицкий В.М. Численные методы: Математический анализ и обыкновенные дифференциальные уравнения. – М.: Изд. «Оникс 21 век», 2005.
- Волков Л.Т. Математические задачи энергетики. Типовые задачи: Учеб пос. – М.: Энергия, 2003. – 120 с.
- Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970. – 664с.
- Дьяконов В. Maple7: учебный курс. – СПб.: Питер, 2002. – 672 с.
- Евдокунин Г.А. Электрические системы и сети / Г.А. Евдокунин. – СПб.: Издательство Сизова М.П., 2001. – 304 с.
- Идельчик В.И. Электрические системы и сети / В.И. Идельчик. – М.: Энергоатомиздат, 1989.– 592 с.
- Курош А.Г. Курс высшей алгебры. – М.: Наука, 1965.
- Лященко М.Я., Головань М.С. Чисельні методи: Підручник. – К.: Либідь, 1996. – 288 с.
- Мельников Н.А. Матричный метод анализа электрических цепей. – М.: Энергия, 1972. – 350 с.
- Неклепаев Б.Н. Электрическая часть электростанций и подстанций: Справочные материалы для курсового и дипломного проектирования / Б.Н. Неклепаев, И.П. Крючков. – М.: Энергоатомиздат, 1989. – 608 с.
- Перхач В.С. Математичні задачі електроенергетики. – Львів.: Вища школа, 1989. – 464 с.
- Расчеты и анализ режимов работы сетей / Под ред. В.А. Веникова. – М.: Энергия, 1974. – 334 с.
- Трусов П.В. Введение в математическое моделирование. – М.: Изд. «Логос», 2004.
- Электрические системы: Математические задачи электроэнергетики/ Под ред. В.А. Веникова. – М.: Высшая школа, 1986. – 288 с.
- Электроэнергетические системы в примерах и иллюстрациях/Под ред. В.А. Веникова. – М.: Энергоатомиздат, 1983. – 504 с.