Методическое пособие по курсу «информатика»
| Вид материала | Методическое пособие |
- Методическое пособие по курсу «Информатика» для студентов, обучающихся по всем направлениям, 1648.11kb.
- С. В. Тимченко информатика 4 Учебно-методическое пособие, 268.2kb.
- Методическое пособие по курсу "Моделирование" для студентов, обучающихся по направлению, 512.51kb.
- Учебно-методическое пособие по курсу «Информационные технологии» для студентов Института, 1419.29kb.
- Учебно-методическое пособие по курсу Геоинформационное картографирование, 606.48kb.
- Методическое пособие для практических занятий красноярск 2002, 894.08kb.
- Методическое пособие по курсу: «История и философия науки», 337.53kb.
- Практикум по курсу "Информатика", 153.44kb.
- Темы рефератов по курсу «Информатика», 10.55kb.
- Современной Гуманитарной Академии (С) современная гуманитарная академия, 2011 методическое, 218.52kb.
Меры информации
Классификация мер
Д
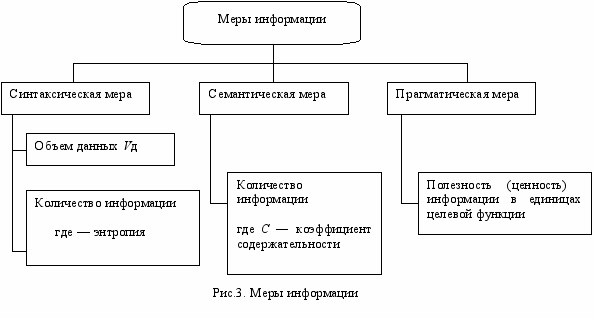ля измерения информации вводятся два параметра: количество информации I и объем данных VД. Эти параметры имеют разные выражения и интерпретацию в зависимости от рассматриваемой формы адекватности. Каждой форме адекватности соответствует своя мера количества информации и объема данных.Синтаксическая мера информации
Возникновение информологии как науки можно отнести к концу 50-х годов нашего столетия, когда американским инженером Р. Хартли была сделана попытка ввести количественную меру информации, передаваемой по каналам связи. Рассмотрим простую игровую ситуацию. До получения сообщения о результате подбрасывания монеты человек находится в состоянии неопределенности относительно исхода очередного броска. Сообщение партнера дает информацию, снимающее эту неопределенность. Заметим, что число возможных исходов в описанной ситуации равно 2, они равноправны (равновероятны) и каждый раз передаваемая информация полностью снимала возникавшую неопределенность. Хартли принял «количество информации», передаваемое по каналу связи относительно двух равноправных исходов и снимающее неопределенность путем оказания на один из них, за единицу информации, получившую название «бит».
Создатель статистической теории информации К. Шеннон обобщил результат Хартли и его предшественников. Его труды явились ответом на бурное развитие в середине века средств связи: радио, телефона, телеграфа, телевидения. Теория информации Шеннона позволяла ставить и решать задачи об оптимальном кодировании передаваемых сигналов с целью повышения пропускной способности каналов связи, подсказывала пути борьбы с помехами на линиях и т.д.
В работах Хартли и Шеннона информация возникает перед нами лишь в своей внешней оболочке, которая представлена отношениями сигналов, знаков, сообщений друг к другу — синтаксическими отношениями. Количественная мера Хартли-Шеннона не претендует на оценку содержательной (семантической) или ценностной, полезной (прагматической) сторон передаваемого сообщения
Эта мера количества информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту.
Объем данных VД в сообщении измеряется количеством символов (разрядов) в этом сообщении. В различных системах счисления один разряд имеет различный вес и соответственно меняется единица измерения данных: в двоичной системе счисления единица измерения — бит (bit — binаry digit — двоичный разряд); в десятичной системе счисления единица измерения — дит (десятичный разряд).
Количество информации I на синтаксическом уровне невозможно определить без рассмотрения понятия неопределенности состояния системы (энтропии системы). Действительно, получение информации о какой-либо системе всегда связано с изменением степени неосведомленности получателя о состоянии этой системы. Пусть до получения информации потребитель имеет некоторые предварительные (априорные) сведения о системе . Мерой его неосведомленности о системе является функция H(), которая в то же время служит и мерой неопределенности состояния системы.
Рассмотрим простой пример. Пусть имеется R0 различных возможных событий («реализаций»), которые априори равновероятны. Например, при бросании монеты мы должны иметь события 1 и 0 и R0 = 2. В случае игральной кости число возможных исходов равно 6, поэтому и R0 = 6. Таким образом, исход бросания монеты или игральной кости интерпретируется как рецепт получения сообщения, и реализуется один из возможных исходов R0. Ясно, что чем больше R0, тем выше неопределенность до получения сообщения и тем большее количество информации приобретается после получения сообщения. Следовательно, все процедуру можно рассматривать так: в самом начале мы не располагали никакой информации I0, т.е. при R0 равновероятных исходах I0 = 0.
В самом конце мы располагаем ненулевой информацией I1 при R1 = 1, т.е. при одном исходе. Предположим, что мы хотим ввести меру количества информации I, которая должна быть связана с R0. Чтобы получить представление о том, какая связь должна быть между R0 и I , потребуем аддитивности I для независимых событий. Таким образом, если мы имеем два независимых множества R01 и R02 , то общее число исходов равно R0 = R01 * R02 , и мы потребуем, чтобы I (R01 * R02) = I (R01) + I (R02).
Этому требованию можно удовлетворить, если выбрать
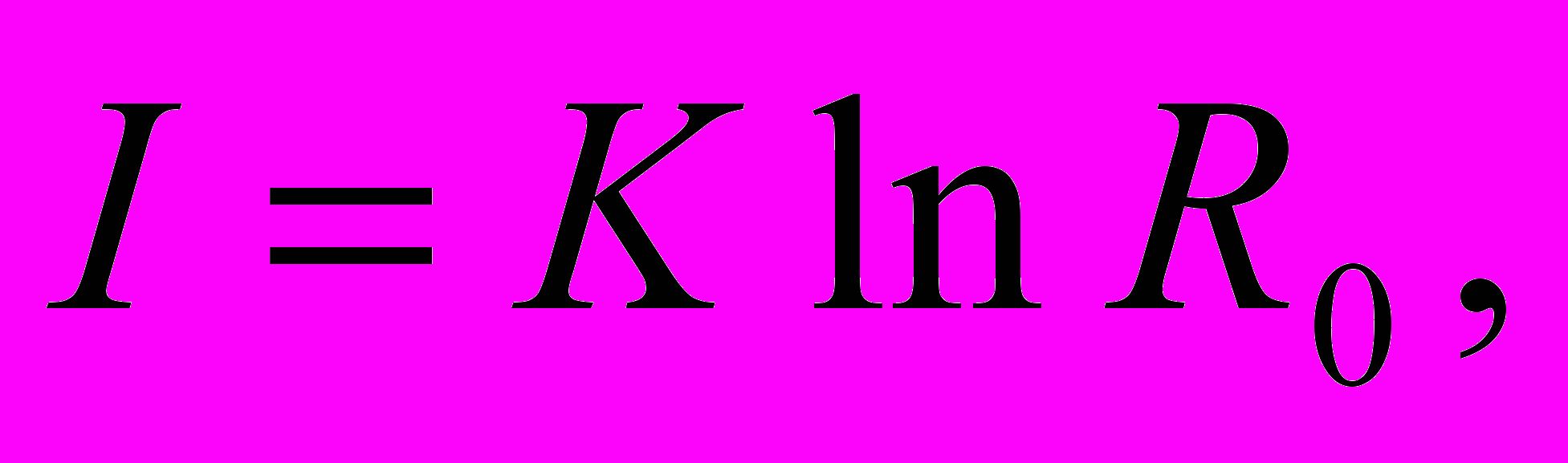
где K — константа. Константа К произвольна и может быть зафиксирована при помощи какого-либо требования. Обычно используется следующее. Рассмотрим так называемую двоичную систему. Построив все возможные слова длины n, мы получим R = 2n реализаций. Мы хотим приравнять количество информации I с числом n в такой системе.
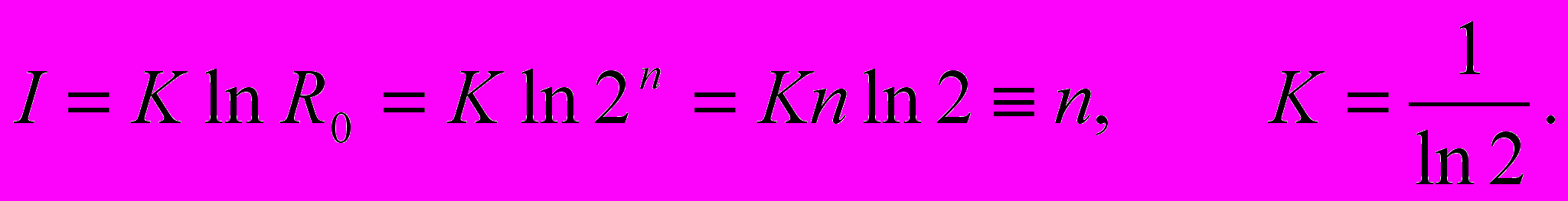
Информация при таком определении измеряется прямо в битах.
После получения некоторого сообщения получатель приобрел некоторую дополнительную информацию I (), уменьшившую его априорную неосведомленность так, что апостериорная (после получения сообщения ) неопределенность состояния системы стала H(). Тогда количество информации I () о системе, полученной в сообщении , определится как
I() = H () – H(),
т.е. количество информации измеряется изменением (уменьшением) неопределенности состояния системы.
Если конечная неопределенность H() обратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации I() = H(). Иными словами, энтропия системы H() может рассматриваться как мера недостающей информации. Энтропия системы H(), имеющая N возможных состояний, согласно формуле Шеннона, равна:
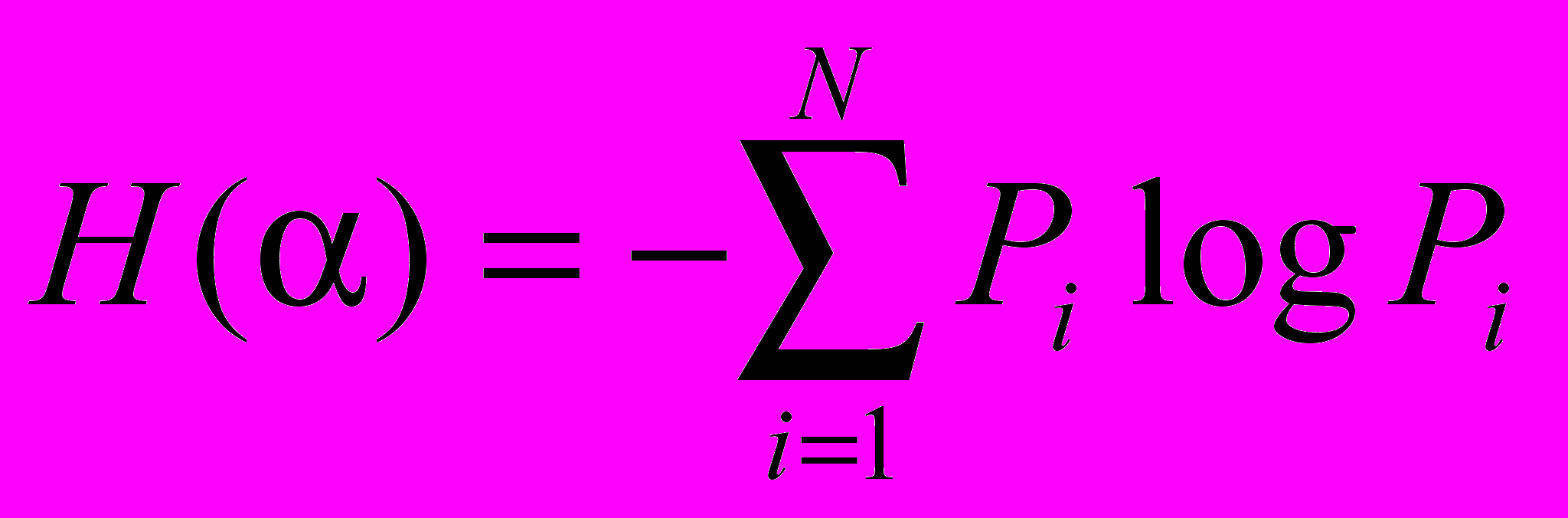,где Рi — вероятность того, что система находится в i-м состоянии.
Для случая, когда все состояния системы равновероятны, т.е. их вероятности равны Pi = 1/N, ее энтропия определяется соотношением
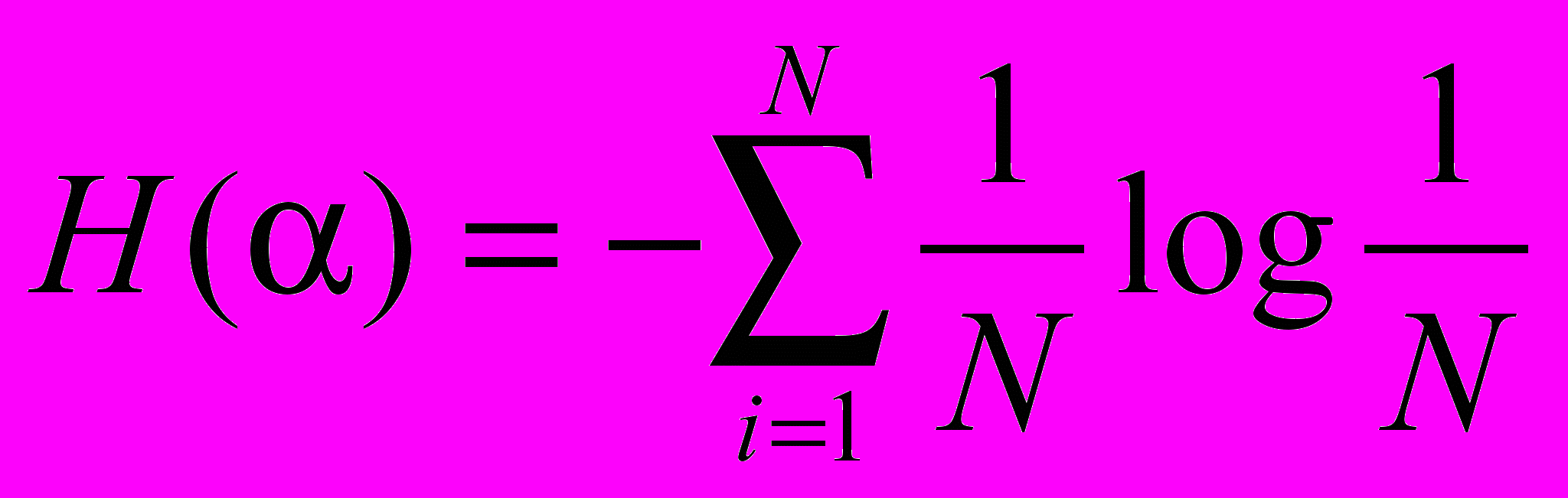
Часто информация кодируется числовыми кодами в той или иной системе счисления, особенно это актуально при представлении информации в компьютере. Естественно, что одно и то же количество разрядов в разных системах счисления может передать разное число состояний отображаемого объекта, что можно представить в виде соотношения
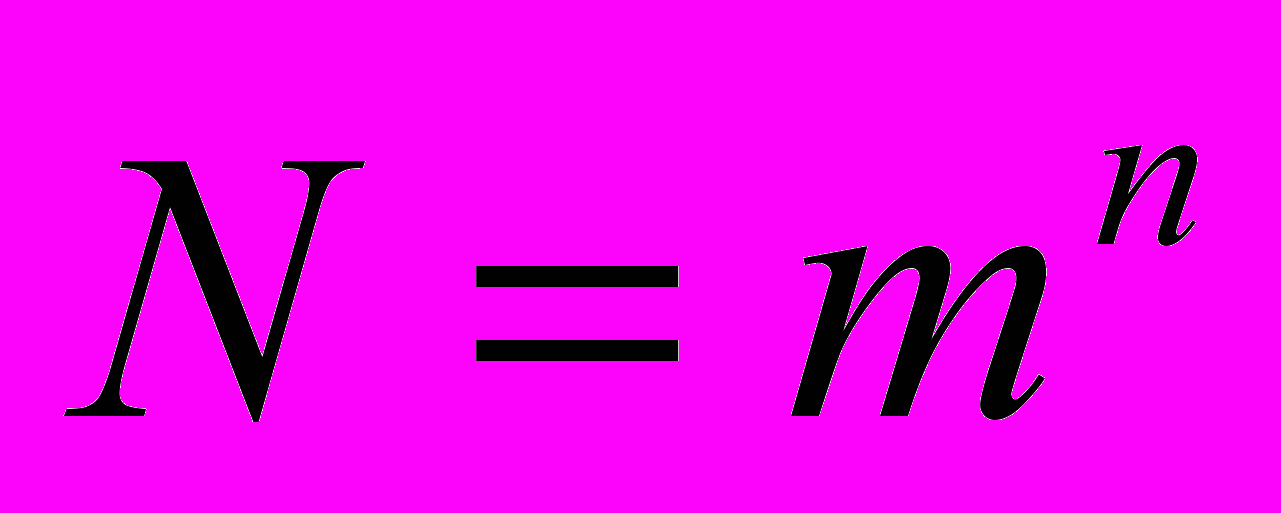,где N — число всевозможных отображаемых состояний; т — основание системы счисления (разнообразие символов, применяемых в алфавите), п — число разрядов (символов) в сообщении.
Наиболее часто используются двоичные и десятичные логарифмы. Единицами измерения в этих случаях будут соответственно бит и дит.
Коэффициент (степень) информативности (лаконичность) сообщения определяется отношением количества информации к объему данных, т.е.
Y = I / VД причем 0 < Y < 1.
С увеличением Y уменьшаются объемы работы по преобразованию информации (данных) в системе. Поэтому стремятся к повышению информативности, для чего разрабатываются специальные методы оптимального кодирования информации.
Семантическая мера информации
Новый этап теоретического расширения понятия информации связан с кибернетикой — наукой об управлении и связи в живых организмах, обществе и машинах. Оставаясь на позициях шенноновского подхода, кибернетика формулирует принцип единства информации и управления, который особенно важен для анализа сути процессов, протекающих в самоуправляющихся, самоорганизующихся биологических и социальных системах. Развитая в работах Н. Винера концепция предполагает, что процесс управления в упомянутых системах является процессом переработки (преобразования) некоторым центральным устройством информации, получаемой от источников
первичной информации (сенсорных рецепторов) и передачи ее в те участки системы, где она воспринимается ее элементами как приказ для выполнения того или иного действия. По совершении самого действия сенсорные рецепторы готовы к передаче информации об изменившейся ситуации для выполнения нового цикла управления. Так организуется циклический алгоритм (последовательность действий) управления и циркуляции информации в системе. При этом важно, что главную роль играет здесь содержание информации, передаваемой рецепторами и центральным устройством. Информация, по Винеру — это «обозначение содержания, полученного из внешнего мира в процессе нашего приспособления к нему и приспособления к нему наших чувств».
Таким образом, кибернетическая концепция подводит к необходимости оценить информацию как некоторое знание, имеющее одну ценностную меру по отношению к внешнему миру (семантический аспект) и другую по отношению к получателю, накопленному им знанию, познавательным целям и задачам (прагматический аспект).
Попытки построить модели понятия информации, охватывающие семантический аспект знания, содержащегося в некотором высказывании относительно обозначаемого объекта, привели к созданию ряда так называемых логико-семантических теорий (Р. Карнап, И. Бар-Хиллел, Дж. Г. Кемени, Е.К. Войшвилло и др.). В них информация рассматривается как уменьшение или устранение неопределенности. Естественно предположить, что средствами какого-либо языка с помощью создаваемых в нем высказываний можно описать некоторую совокупность возможных ситуаций, состояний, альтернатив. Семантическая информация, содержащаяся в каком-либо высказывании, исключает некоторые альтернативы. Чем больше альтернатив исключает высказывание, тем большую семантическую информацию оно несет. Так, например, одна из возможных совокупностей ситуаций может быть описана следующим образом: «все тела при нагревании расширяются». Высказывание «металлы при нагревании расширяются» исключает все альтернативы в которых речь может идти о неметаллах. Семантическая сила высказывания может быть оценена отношением все тела(все металлы). Еще более информативным будет высказывание "железо при нагревании расширяется", так как оно исключает все альтернативы, кроме одной.
При всем многообразии логико-семантических теорий им присущи общие черты, они указывают путь решения трех связанных друг с другом проблем: определения совокупности возможных альтернатив средствами выбранного языка, количественной оценки альтернатив, их относительного сопоставления (взвешивания), введения меры семантической информации.
В рассмотренных теоретических конструкциях - статистической и семантической информации — речь шла о потенциальной возможности извлечь из передаваемого сообщения какие-либо сведения. Вместе с тем в процессах информационного обмена очень часто складываются ситуации, в которых мощность или качество информации, воспринимаемое приемником, зависит от того, насколько он подготовлен к ее восприятию.
Понятие тезауруса является фундаментальным в теоретической модели семантической теории информации, предложенной Ю.А. Шрейдером и учитывающей в явной форме роль приемника. Согласно этой модели, тезаурус — это знания приемника информации о внешнем мире, его способность воспринимать те или иные сообщения, а информация — это разность тезаурусов. Представим себе, что до получения телеграммы «Встречай завтра рейс СУ172» мы из вчерашнего разговора по междугороднему телефону уже знали о предстоящем приезде своего родственника или друга, а наведя справки, узнали и номер авиарейса, с которым он может прибыть в город. Наш тезаурус уже содержал информацию, заключенную в телеграмме. Следовательно, он не изменился с ее получением, и семантическая ценность этой информации оказалась нулевой. Очевидно, что к подобной оценке семантического содержания информации примешивается семантический аспект, скрытый в изначальной «установке» тезауруса на осмысление принимаемого сообщения.
Для измерения смыслового содержания информации, т.е. ее количества на семантическом уровне, наибольшее признание получила тезаурусная мера, которая связывает семантические свойства информации со способностью пользователя принимать поступившее сообщение. Для этого используется понятие тезаурус пользователя — совокупность сведений, которыми располагает пользователь или система.
В
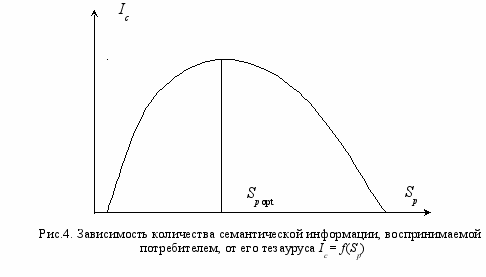
зависимости от соотношений между смысловым содержанием информации S и тезаурусом пользователя Sр изменяется количество семантической информации Iс, воспринимаемой пользователем и включаемой им в дальнейшем в свой тезаурус. Характер такой зависимости показан на рис. 4. Рассмотрим два предельных случая, когда количество семантической информации Iс равно 0: при Sр 0 пользователь не воспринимает, не понимает поступающую информацию; при Sр пользователь все знает, и поступающая информация ему не нужна.
Максимальное количество семантической информации Iс потребитель приобретает при согласовании ее смыслового содержания S со своим тезаурусом Sр (Sр = Sр opt), когда поступающая информация понятна пользователю и несет ему ранее не известные (отсутствующие в его тезаурусе) сведения. Следовательно, количество семантической информации в сообщении, количество новых знаний, получаемых пользователем, является величиной относительной. Одно и то же сообщение может иметь смысловое содержание для компетентного пользователя и быть бессмысленным (семантический шум) для пользователя некомпетентного. При оценке семантического (содержательного) аспекта информации необходимо стремиться к согласованию величин S и Sр. Относительной мерой количества семантической информации может служить коэффициент содержательности С, который определяется как отношение количества семантической информации к ее объему:
C = Ic/Vд.
Прагматическая мера информации
В прагматических концепциях информации этот аспект является центральным, что приводит к необходимости учитывать ценность, полезность, эффективность, экономичность информации, т.е. те ее качества, которые определяющим образом влияют на поведение самоорганизующихся, самоуправляющихся, целенаправленных кибернетических систем (биологических, социальных, человеко-машинных).
Одним из ярких представителей прагматических теорий информации является поведенческая модель коммуникации — бихевиористская модель Акоффа-Майлса. Исходным в этой модели является целевая устремленность получателя информации на решение конкретной проблемы. Получатель находится в «целеустремленном состоянии», если он стремится к чему-нибудь и имеет альтернативные пути неодинаковой эффективности для достижения цели. Сообщение, переданное получателю иформативно, если оно изменяет его «целеустремленное состояние».
Так как «целеустремленное состояние» характеризуется последовательностью возможных действий (альтернатив), эффективностью действия и значимостью результата, то передаваемое получателю сообщение может оказывать воздействие на все три компонента в различной степени. В соответствии с этим передаваемая информация различается по типам на «информирующую», «инструктирующую» и «мотивирующую». Таким образом, для получателя прагматическая ценность сообщения состоит в том, что оно позволяет ему наметить стратегию поведения при достижении цели построением ответов на вопросы: что, как и почему делать на каждом очередном шаге? Для каждого типа информации бихевиористская модель предлагает свою меру, а общая прагматическая ценность информации определяется как функция разности этих количеств в «целеустремленном состоянии» до и после его изменения на новое «целеустремленное состояние».
Следующим этапом в развитии прагматических теорий информации явились работы американского логика Д. Харраха, построившего логико-прагматическую модель коммуникации. Одной из слабостей бихевиористской модели является ее неподготовленность к оценке ложных сообщений. Модель Харраха предполагает учет общественного характера человеческой коммуникации. В соответствии с ней получаемые сообщения должны быть сначала подвергнуты обработке, после которой выделяются сообщения «годные к употреблению». Именно с совокупности годных к употреблению сообщений должны быть применены критерии прагматической ценности.
Эта мера определяет полезность информации (ценность) для достижения пользователем поставленной цели. Эта мера также величина относительная, обусловленная особенностями использования этой информации в той или иной системе. Ценность информации целесообразно измерять в тех же самых единицах (или близких к ним), в которых измеряется целевая функция.
In() = П(/) – П(),
где In() — ценность информационного сообщения для системы управления , П() — априорный ожидаемый экономический эффект функционирования системы управления , П(/) — ожидаемый эффект функционирования системы при условии, что для управления будет использована информация, содержащаяся в сообщении .
Теория информации «в смысле Шеннона» возникла как средство решения конкретных прикладных задач в области передачи сигналов по каналам связи. Поэтому, по-существу, она являлась и является прикладной информационной наукой. Семейство таких наук, специально изучающих информационные процессы в том или ином их специфическом содержании и форме, во второй половине нашего века растет довольно быстро. Это — кибернетика, теория систем, документалистика, лингвистика, символическая логика и др. Стержнем, объединяющим все эти исследования, служит общая теория информации — «информология», в основу которой и положены синтаксические, семантические и прагматические концепции информации.