Программа социологического исследования. 27 Методы сбора социологической информации

Вид материала

Программа

Содержание 2. Найти все числа вида , кратные 36. Признаки делимости.

Подобный материал:

• Программа социологического исследования Основные методы сбора социологической информации, 23.08kb.
• Правила составления социологической анкеты. Опрос экспертов как метод социологического, 15.89kb.
• Методика социологического исследования Вопросы, 57.73kb.
• «Использование информационных технологий для сбора социологической информации», 523.33kb.
• Планы семинарских занятий по дисциплине " методология исследований в социальных и поведенческих, 403.79kb.
• Программа социологического исследования > Методы сбора данных в эмпирическом исследовании, 282.77kb.
• М. В. Ломоносова В. И. Добреньков, А. И. Кравченко методы социологического исследования, 11794.41kb.
• Рабочий план социологического исследования. Функции и основные элементы программы социологического, 17.2kb.
• Отчет о ходе и результате социологического исследования. Анкета (опросный лист), 138.6kb.
• Автор программы: Даудрих Н. И. Рекомендована секцией умс, 522.38kb.

Задание 3


Числа a и b при делении на 13 дают соответственно остатки 8 и 5. Какой остаток при делении на 13 даст их сумма, разность, произведение?

При выполнении данного задания надо воспользоваться формулой деления с остатком.

Определение. Пусть a и b – натуральные числа. Неполным частным q и остатком r при делении a на b называются такие целые неотрицательные числа, что a = bq + r, причем

0 ≤ r ≤ b.

Число а при делении на 13 дает остаток 8, поэтому а = 13q + 8. Число b при делении на 13 дает остаток 5, поэтому b = 13р + 5. Найдем сумму чисел a и b.

Имеем: a + b = (13q + 8) + (13р + 5) = (13q + 13р) + (8 +5) = 13(q + р) + 13 = 13(q + р + 1) = 13g, где g = (q + р + 1). Таким образом, сумма чисел a и b при делении на 13 дает остаток 0, т.е. кратна 13.

Найдем разность чисел a и b. Имеем a – b = (13 q + 8) × (13р + 5) = (13q – 13р) + (8 - 5) = 13(q + р) – 3 = 13g – 3. Таким образом, разность чисел a и b при делении на 13 дает остаток 3, т.е. r = 3.

Найдем произведение чисел a и b .Имеем: a – b = (13q + 8) × (13p + 5) = 169pq + 104p + 65q + 40 = (169pq + 104p + 65q + 39) + 1 = 13(13pq + 8p + 5q + 3) + 1, где g = 13pq + 8p + 5q + 3.

Таким образом, произведение числа а и b при делении на 13 дает остаток 1, т.е. r = 1.


Задание 4

Найти наименьшее общее кратное и наибольший общий делитель (двумя способами) чисел: 64260 и 75735.

Общим делителем натуральных чисел a и b называется число, на которое одновременно делятся числа a и b. Наибольший из всех общих делителей чисел a и b называется их наибольшим общим делителем. Обозначается НОД(a,b).

Кратным натуральных чисел a и b называется число, которое кратно числу a и числу b одновременно. Наименьшее из всех кратных чисел a и b называется их наименьшим общим кратным. Обозначается НОК(a,b).

Наибольший общий делитель чисел a и b можно найти двумя способами:

1. Чтобы найти наибольший общий делитель чисел a и b, надо разложить эти числа на простые множители, т.е. представить их в каноническом виде: 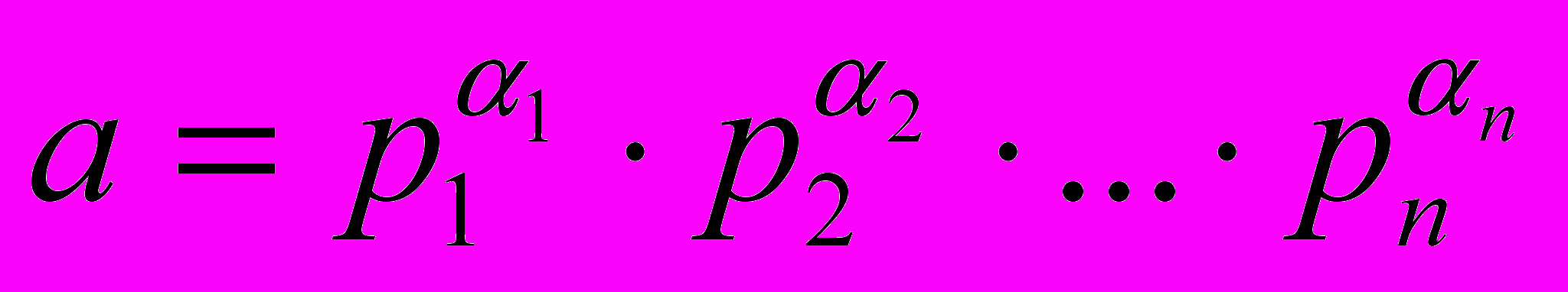и 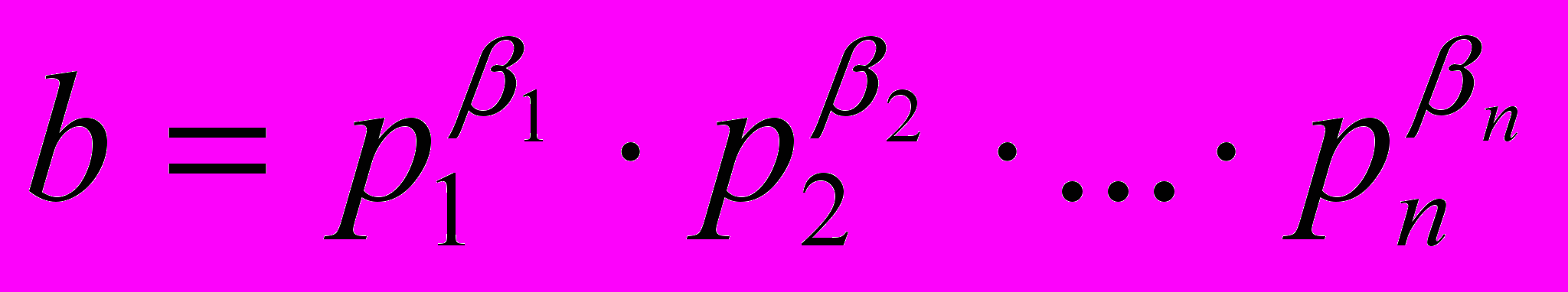. Наибольший общий делитель натуральных чисел a и b равен произведению одинаковых простых множителей, входящих в данные разложения, с наименьшими показателями степени.

2. Наибольший общий делитель натуральных чисел a и b находят с помощью алгоритма Евклида. Он основан на следующих трех утверждениях:

а) Если а делится на b, то делитель чисел a и b равен b.

б) Если при делении а на b получается остаток r, то делитель чисел a и b равен делителю чисел b и r, и задача сводится к отысканию наибольшего общего делителя чисел b и r.

в) Если b делится на r, то наибольший общий делитель чисел b и r равен r. Тогда и наибольший общий делитель чисел a и b равен r. Если же при делении b на r получается остаток r₁, тогда делитель чисел r и r₁ такой же, что и делитель чисел b и r, и, следовательно, такой же, как делитель чисел a и b.

Продолжая описанный процесс, получаем все меньшие и меньшие остатки. В конце концов, дойдем до остатка, на который будет делиться предыдущий остаток. Этот наименьший, отличный от 0 остаток и будет наибольшим общим делителем чисел a и b.

Наименьшее общее кратное тоже можно найти двумя способами.

1. Чтобы найти наименьшее общее кратное чисел a и b, надо разложить эти числа на простые множители, т.е. представить их в каноническом виде: 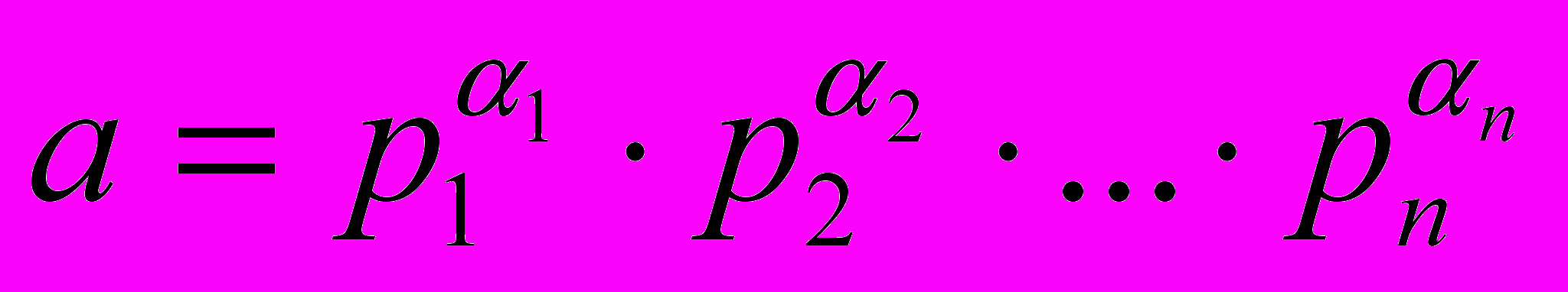и 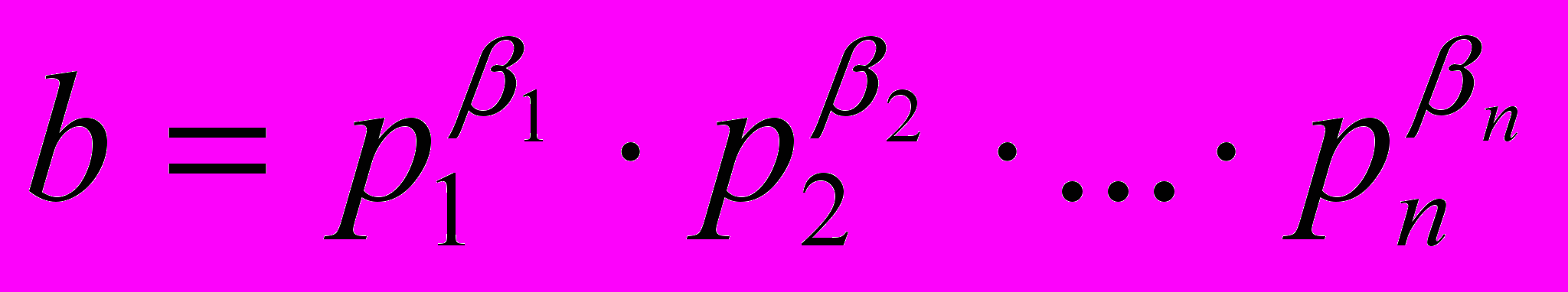. Наименьшее общее кратное натуральных чисел а и b равно произведению всех простых множителей, входящих в данные разложения, с наибольшими показателями степени.

2. Известно, что наименьшее общее кратное и наибольший общий делитель чисел а и b связаны соотношением: НОК (a,b) НОД (a,b) = а  b. Отсюда находим .

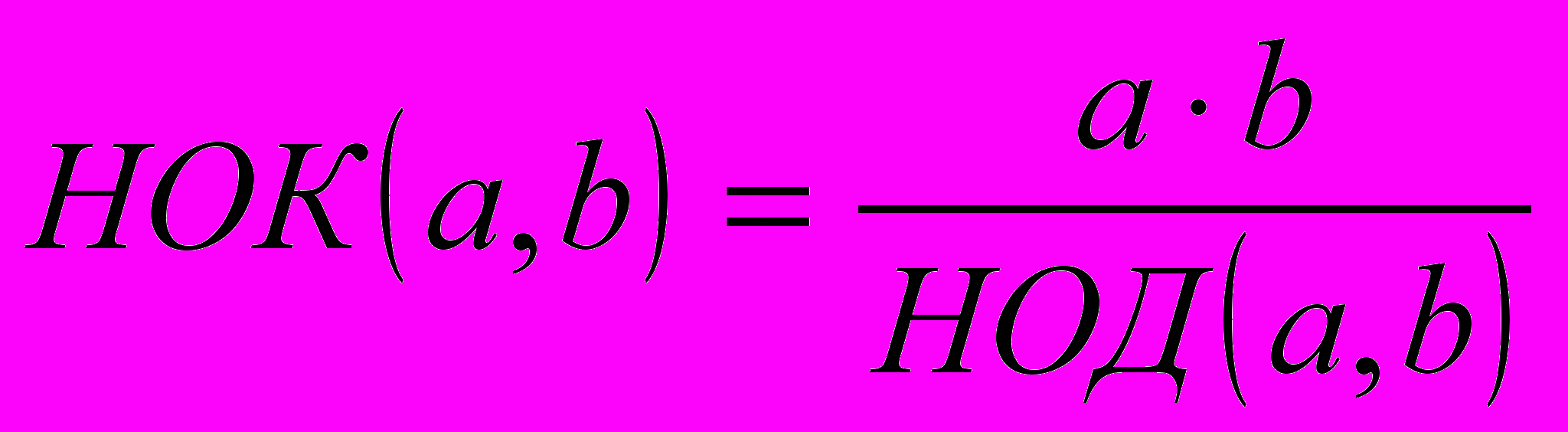Используя приведенные выше теоретические положения, найдем наибольший общий делитель и наименьшее общее кратное чисел а и b.

Найдем наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) чисел 64260 и 75735 двумя способами.


1 способ. Разложим числа 64260 и 75735 на простые множители. Имеем:

64260 2 75735 3

32130 2 25245 3

16065 3 8415 3

5355 3 2805 3

1785 3 935 5

595 5 187 11

119 7 17 17

17 17


Таким образом, получили: и 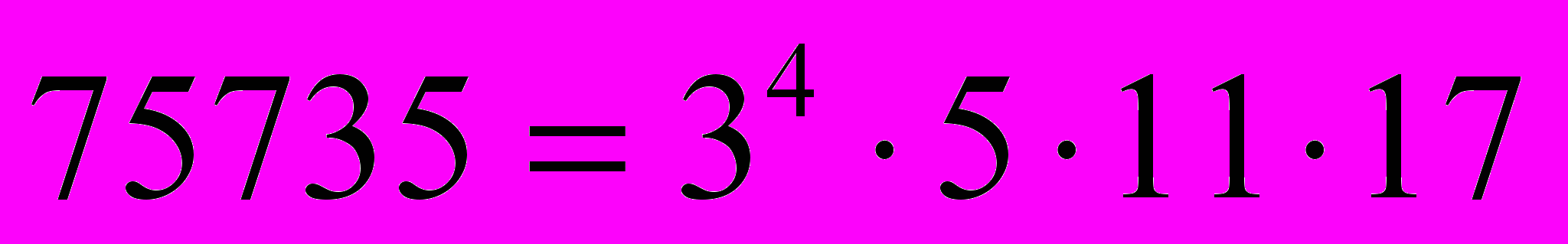. Отсюда получаем, что НОД(64260, 75735) = 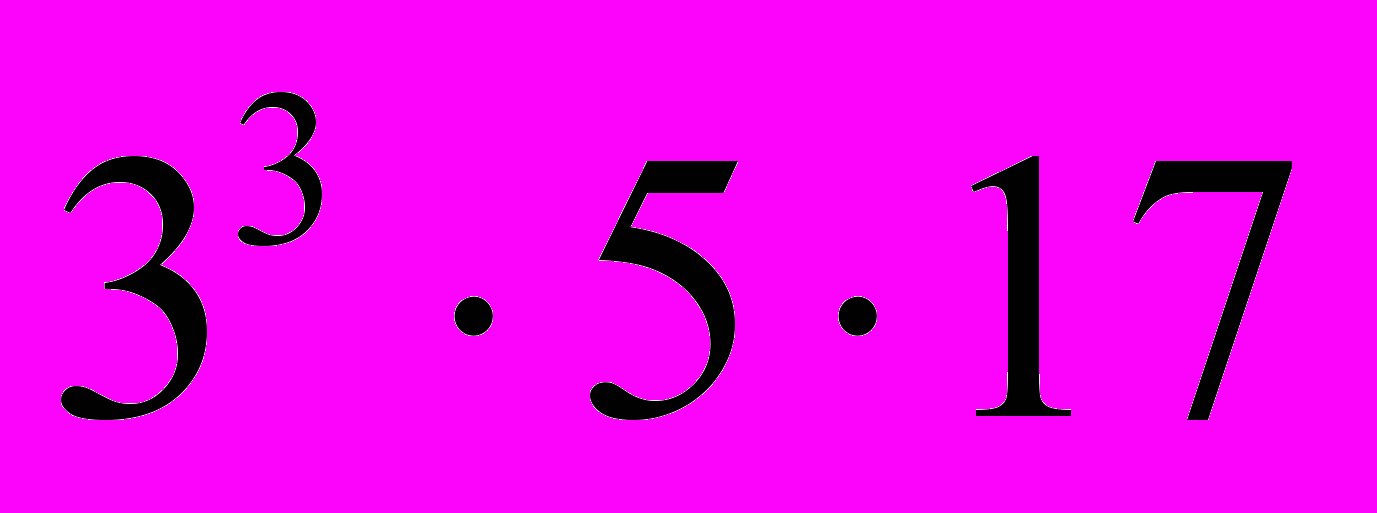= 2295 и НОК(64260, 75735) = 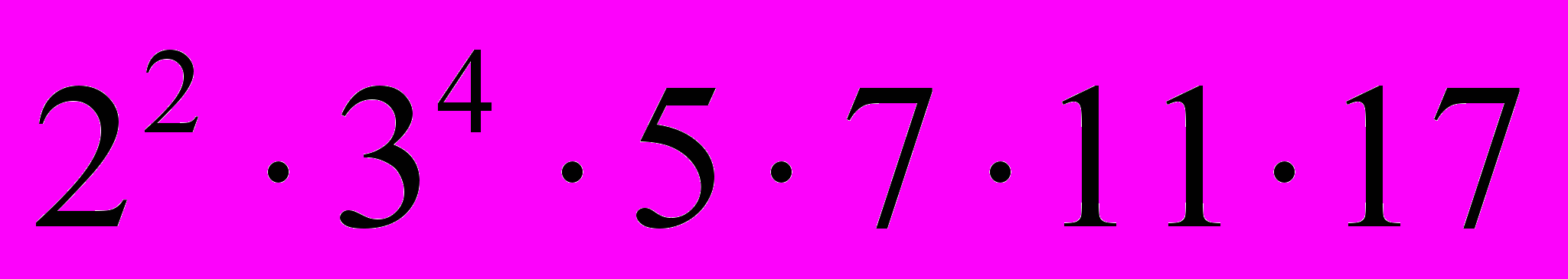= 2120580.

2 способ. Найдем наибольший общий делитель чисел 64260 и 75735 с помощью алгоритма Евклида. Разделим 64260 на 75735 с остатком. Имеем:

_75735 64260 _64260 11475 _11475 6885 _6885 4590 _4590 2295

64260 1 57375 5 6885 1 4590 1 4590 2

11475 = r₁ 6885 = r₂ 4590 = r₃ 2295 = r₄ 0 = r₅

Таким образом, последний, отличный от 0 остаток r₄ = 2295.

Следовательно, НОД(64260, 75735) = 2295.

Найдем НОК(64260, 75735). Имеем а  b = 64260  75735, тогда НОК(64260, 75735) = .

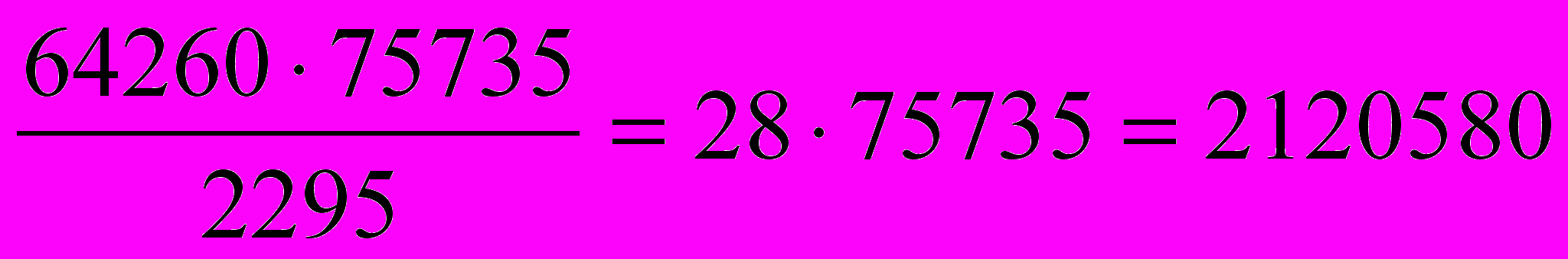Задание 5

1. Среди данных чисел найти простые: 4869, 279, 8345, 223, 847;

2. Найти все числа вида 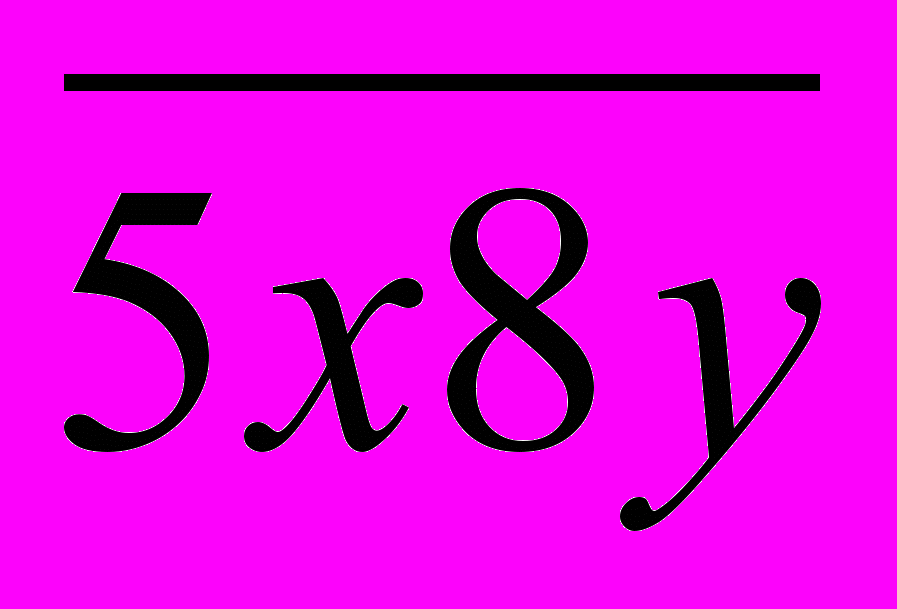, кратные 36.

1. Для выполнения этого задания надо знать определение простого и составного числа, признаки делимости на 2, 3, 5, 9, 11 и способ нахождении простых чисел.

Число называется простым, если оно имеет ровно два делителя, единицу и само себя. Число называется составным, если оно имеет больше двух делителей.

Признаки делимости. Натуральное число делится на два, если оно оканчивается на 0, 2, 4, 6, 8.

Натуральное число делится на 3 (на 9), если сумма цифр в десятичной записи этого числа делится на 3 (на 9).

Натуральное число делится на 5, если оно оканчивается на 0 или 5.

Натуральное число делится на 7, 11, 13, если …?

Теорема. Наименьший простой делитель составного числа а не превосходит .

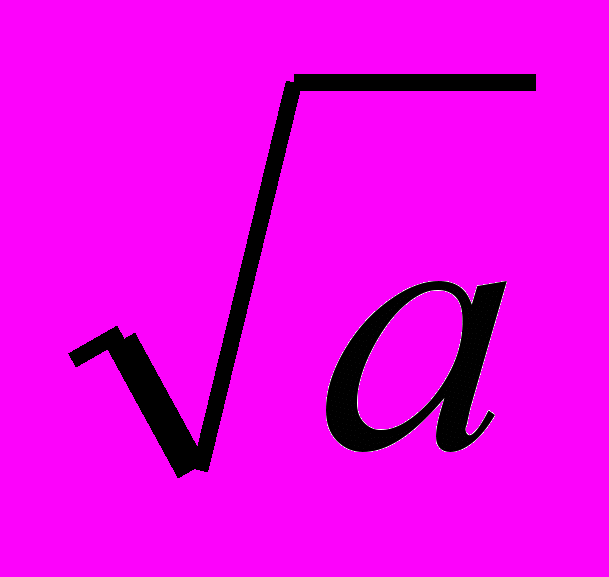Найдем среди чисел 486, 279, 8345, 223 и 847 простые. По признаку делимости на 2 заключаем, что число 8345 делится на 5.

Проверим, делятся ли числа 279, 223, 847 на 3. Найдем сумму цифр числа 279: 2+7+9=18, 18 делится на 3, следовательно, число 279 делится на 3. Найдем сумму цифр числа 223: 2+2+3=7, 7 не делится на 3, следовательно, число 223 не делится на 3. Найдем сумму цифр числа 847: 8+4+7=19, 19 не делится на 3, следовательно, число 847 не делится на 3.

Проверим делимость чисел 223 и 847 на 7. Так как числа трехзначные, проверить их делимость на 7 можно непосредственно делением. Проверка показывает, что число 223 не делится на 7, а число 847 делится на 7. Следовательно, число 847 составное.

Рассмотрим число 223. 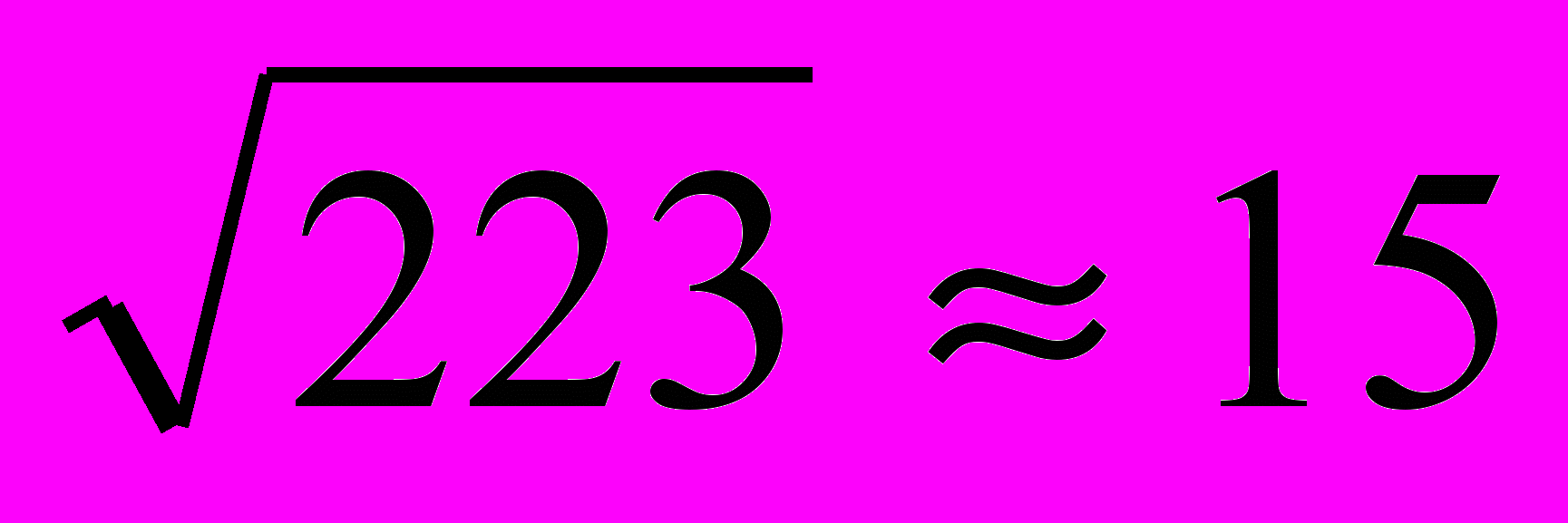. Выпишем все простые числа, меньше 15: 2, 3, 5, 7, 11, 13. Число 223 не делится на 2, 3, 5, 7. проверим, делится ли оно на 11 или 13. Непосредственным делением убеждаемся, что 223 не делится на 11 и 13. Следовательно, данное число простое.

2. Найдем все числа вида 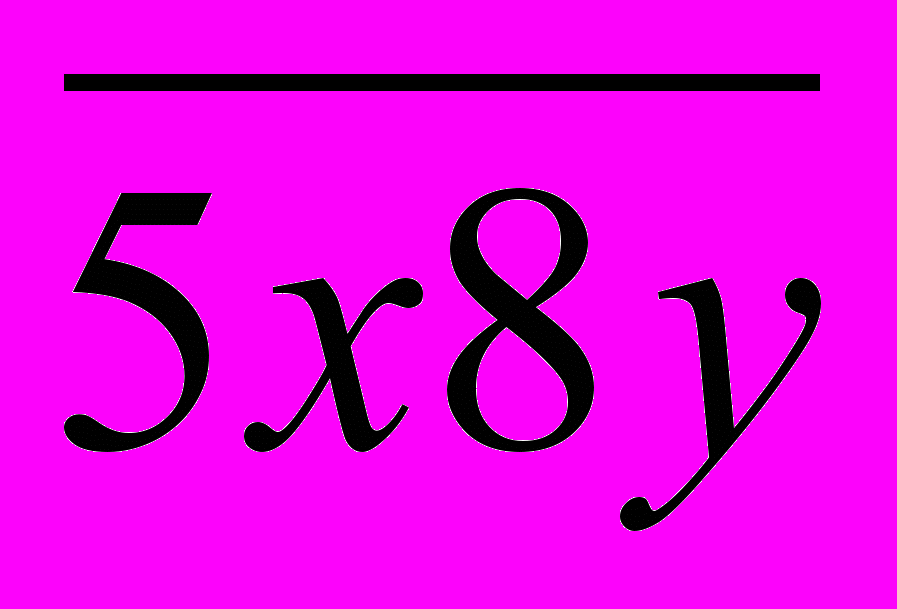, кратные 36. 36 – составное число, 36=4·9. Следовательно, чтобы число было кратно 36, надо, чтобы оно было кратно 4 и 9.

Найдем, при каких значениях у данное число будет кратно 4. Воспользуемся признаком делимости на 4: данное число делится на 4, если число, образованное двумя последними цифрами в его десятичной записи, делится на 4.

Число, образованное двумя последними цифрами в его десятичной записи нашего числа, будет 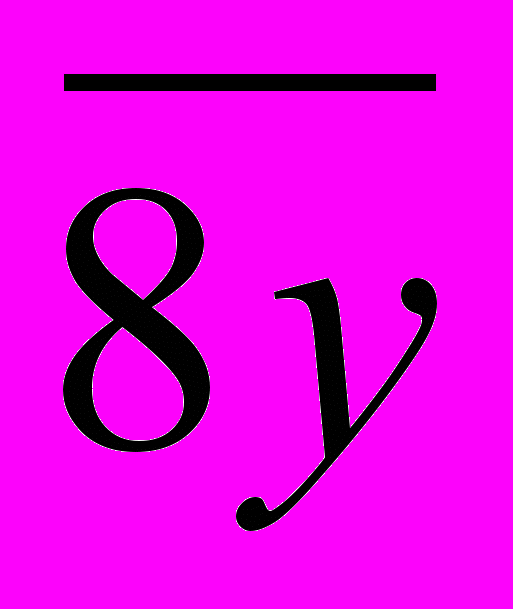. Оно будет делиться на 4 тогда, когда у = 4 и у = 8. Подставив найденные значения у в число 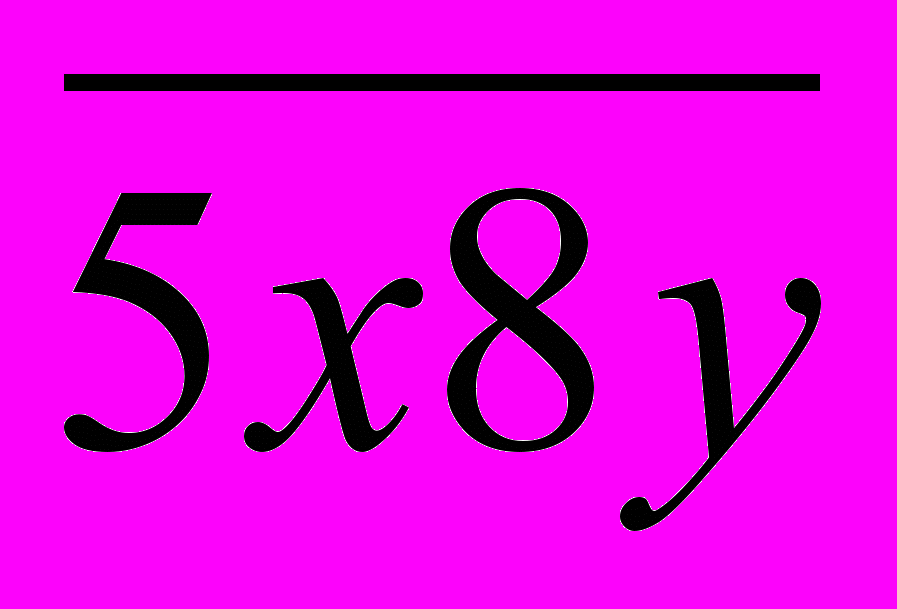получим два числа: 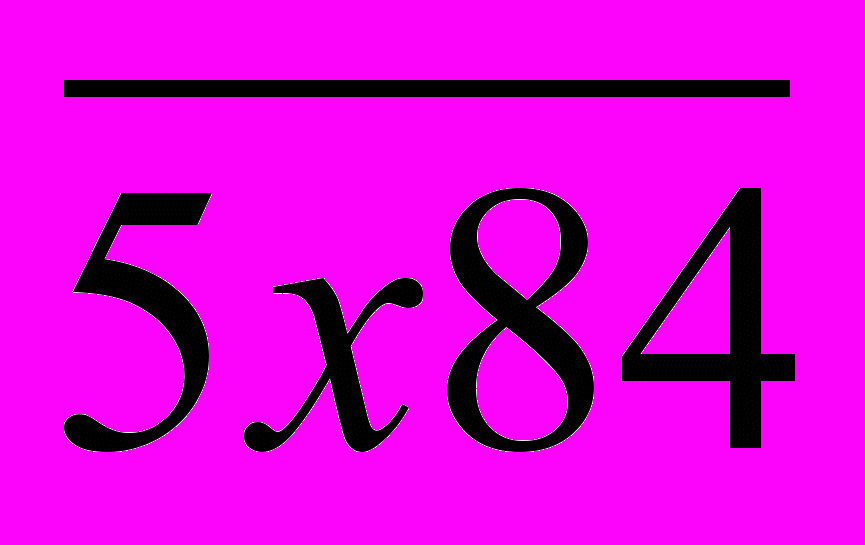и .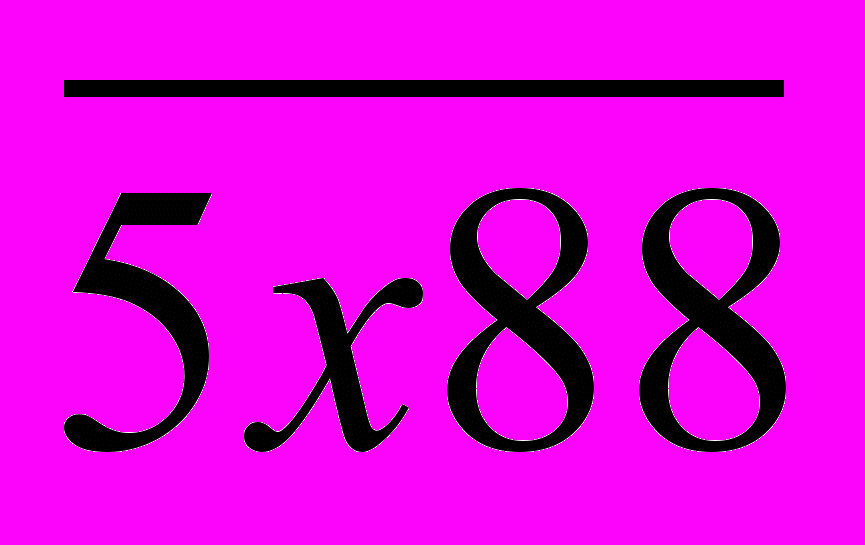

Чтобы число делилось на 9, необходимо, чтобы сумма цифр в его десятичной записи была кратна 9. Найдем сумму цифр числа 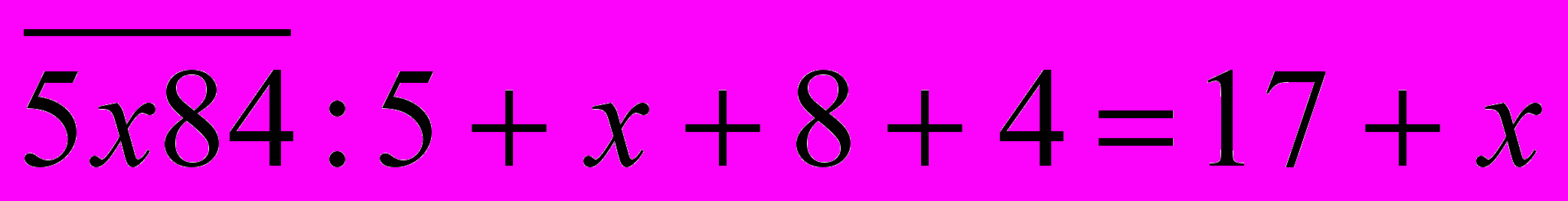. Данная сумма кратна 9 при х = 1 (17 + 1 = 18). Подставив найденное значение х в 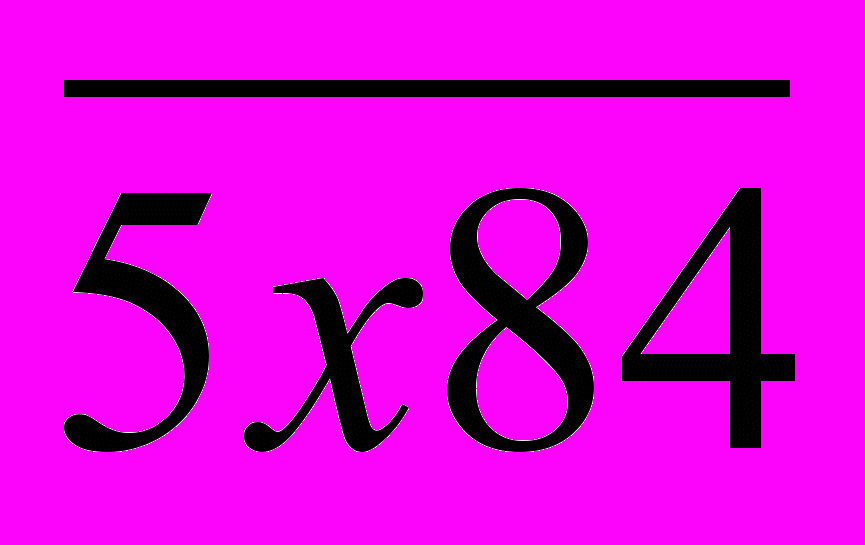, получим число 5184, которое будет делиться на 9. А так как это число делится и на 4, то оно будет делиться на 36. Других значений х нет, так как х должно быть однозначным числом. Рассмотрим число 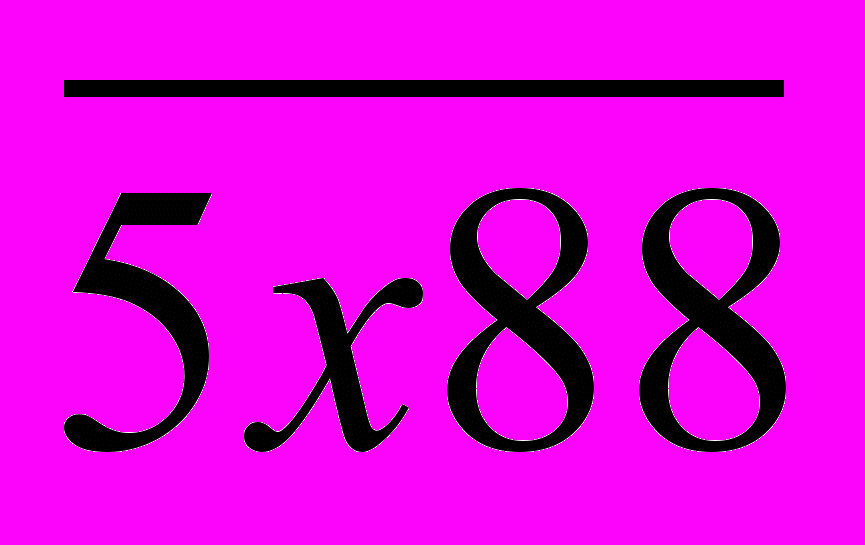, найдем сумму его цифр: 5 + х + 8 + 8 = 21 + х. Данная сумма кратна 9 только при х = 6. подставив найденное значение х в 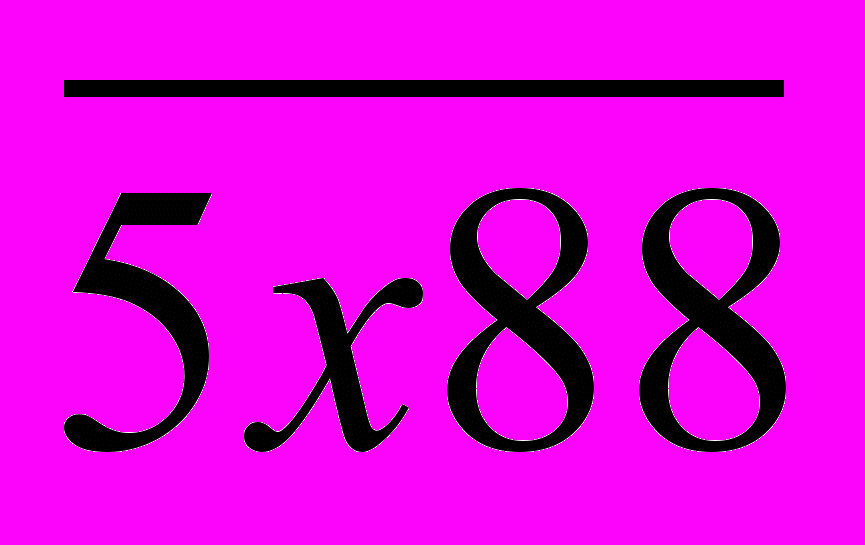, получим число 5688, которое будет делиться на 9. А так как это число делится и на 4, то оно будет делиться на 36.

Таким образом, числами, кратными 36, будут: 5184 и 5688.


Вопросы к экзамену по естествознанию (землеведение)

для студентов 2 курса ОЗО ПФ – 5,5


1. Современные представления о составе и строении Вселенной.

2. Звезды. Классификация звезд.

3. Происхождение Вселенной.

4. Модель расширяющейся Вселенной.

5. Эволюция и строение галактики.

6. Состав и строение Солнца и солнечной системы.

7. Классификация планет. Характеристика внутренних и внешних планет.

8. Ориентирование и измерение расстояний на местности.

9. Глобус и градусная сеть.

10. План и географические карты.

11. Условные знаки.

12. Счет времени.

13. Картографические проекции.

14. Первые представления о фигуре Земли.

15. Внутреннее строение Земли. Размеры Земли.

16. Современные представления о фигуре Земли.

17. Значение шарообразной фигуры Земли.

18. Осевое движение Земли и его следствия.

19. Обращение Земли вокруг Солнца.

20. Геохронология Земли.

21. Магнитное поле Земли.

22. Рельеф, его формы и типы. Рельефообразующие факторы. Литосфера.

23. Эндогенные (внутренние) рельефообразующие процессы.

24. Экзогенные (внешние) рельефообразующие процессы.

25. Закономерности в распределении воды и суши на Земной поверхности

26. Формы рельефа поверхности суши Земли.

27. Минералы: определение, классификация, физические свойства.

28. Плоскогорья, расположенные на территории России.

29. Возвышенности СНГ.

30. Равнины СНГ.

31. Горы СНГ.

32. Горные породы: определение, классификация.

33. Понятие о гидросфере. Мировой круговорот воды.

34. Свойства воды и ее роль в природе и жизни человека. Аномалии воды.

35. Характеристика Мирового океана: соленость, температура, движение воды океана.

36. Жизнь в Мировом океане. Ресурсы Мирового океана.

37. Подземные воды

38. Река. Характеристика реки. Реки СНГ.

39. Озера: определение, классификация, происхождение. Озера СНГ.

40. Состяв, строение и значение атмосферы.

41. Нагреваемость атмосферы: солнечная радиация, температура воздуха.

42. Вода в атмосфере. Конденсация и сублимация пара у поверхности Земли.

43. Облака, их типы. Образование облаков, их виды. Атмосферные осадки.

44. Воздух атмосферы: движение воздуха, воздушные массы и фронты.

45. Погода. Элементы погоды и явления. Типы погоды.

46. Климат и климатические ресурсы России.

47. Почвы, их строение, состав. Факторы почвообразования. Закономерности распределения почв в России.

48. Современные представления о биосфере по Вернадскому: строение и состав.

49. Географическое положение и рельеф Тюменской области.

50. Почвы Тюменской области.

51. Природные зоны Тюменской области.

52. Растительный мир природных зон Тюменской области

53. Животный мир природных зон Тюменской области.