Лекция 8 Лекция колебания в системах со многими степенями свободы

Вид материалаЛекция

Содержание


М может стоять как плюс
Подобный материал:

ЛЕКЦИЯ 8


Лекция 8.
КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ


Д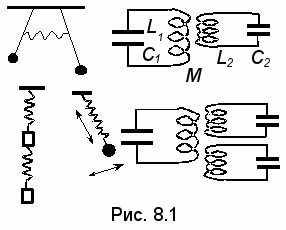о сих пор одной обобщенной координаты (будь то смещение, заряд и т.п.) было достаточно, чтобы вполне определить состояние системы, совершающей колебания. На рис. 8.1 показаны другие системы, описание которых потребует
i координат - степеней свободы - и соответственно столько же дифференциальных уравнений. Такие системы, естественно, являются более сложными не только в количественном отношении - возникают и новые качественные изменения.

Рассмотрим систему с двумя степенями свободы, представляющую собой два колебательных контура без затухания (L1, C1; L2, C2), соединенных индуктивной связью c коэффициентом взаимной индукции M. Благодаря связи, при протекании тока J1­ через первый (левый) контур, будет появляться ток и во втором (правом) контуре. И наоборот. Поэтому для зарядов q1,q2 получим

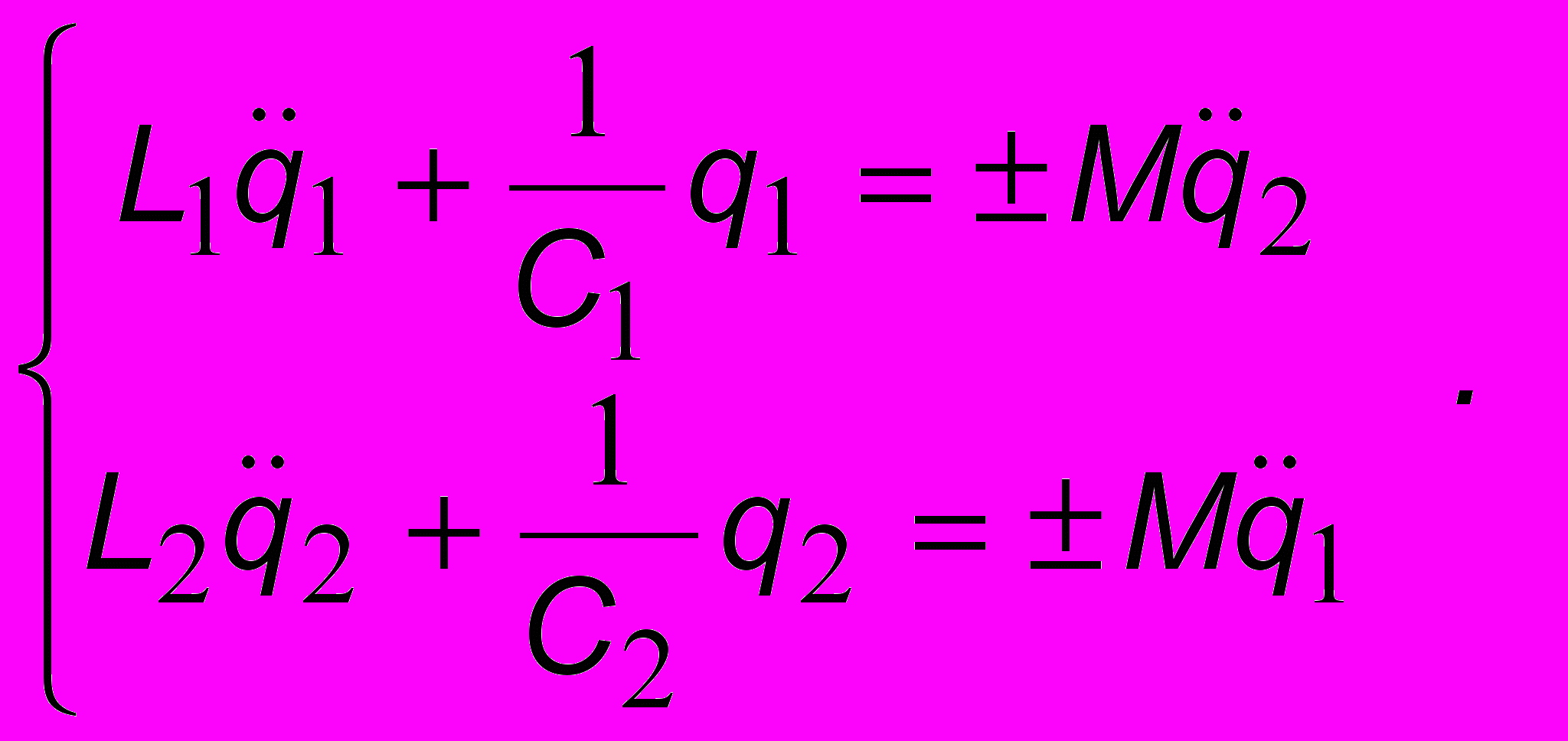(8.1)

При этом в зависимости от способа включения катушек перед М может стоять как плюс, так и минус. Включим катушки так, чтобы был минус. Поделив первое уравнение системы на L1, а второе - на L2 и обозначая 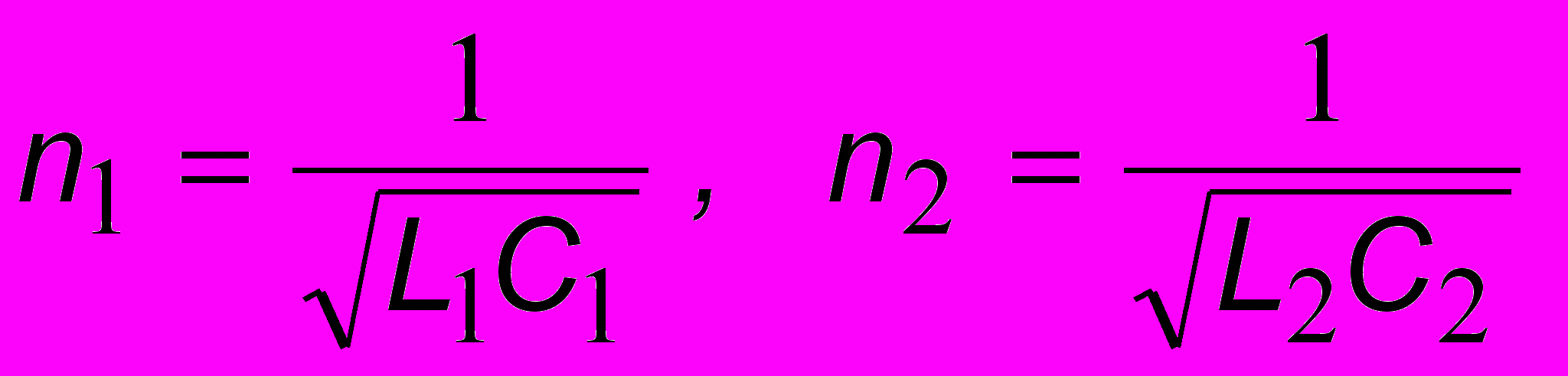, получим

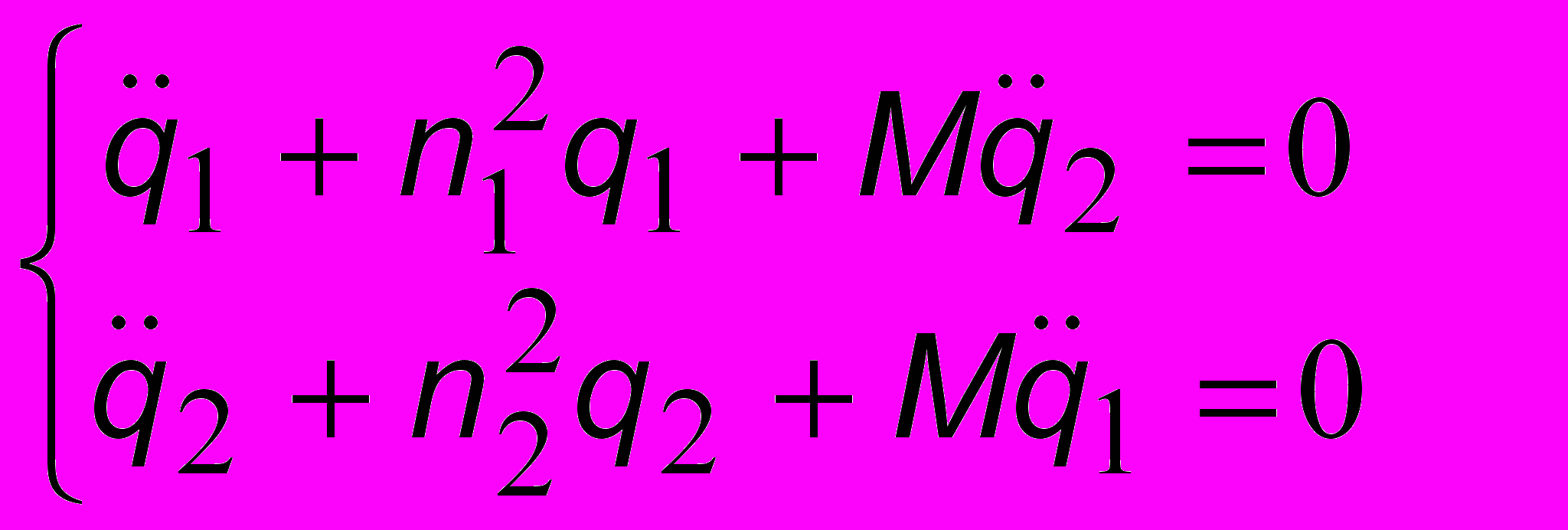. (8.1а)

Параметры n1 n2 называются парциальными частотами (от латинского parte - часть). Каждая из них равна собственной циклической частоте, которую имел бы данный контур в отсутствие второго (или же в отсутствие связи со вторым). Будем искать решение (8.1а) в виде

q 1 = A cos(t+); q 2 = B cos(t+).

Находя производные 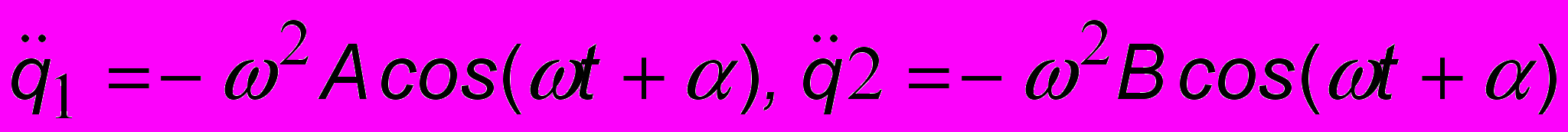и подставляя их в (8.1а), получим систему двух линейных уравнений для А и В, решение которой возможно в случае, если детерминант системы равен нулю:


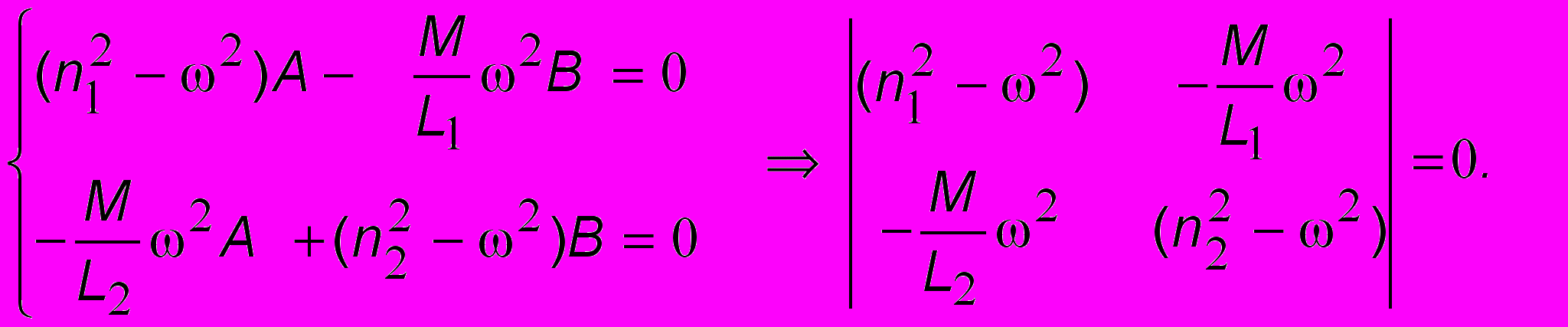(8.2)


Отсюда получим 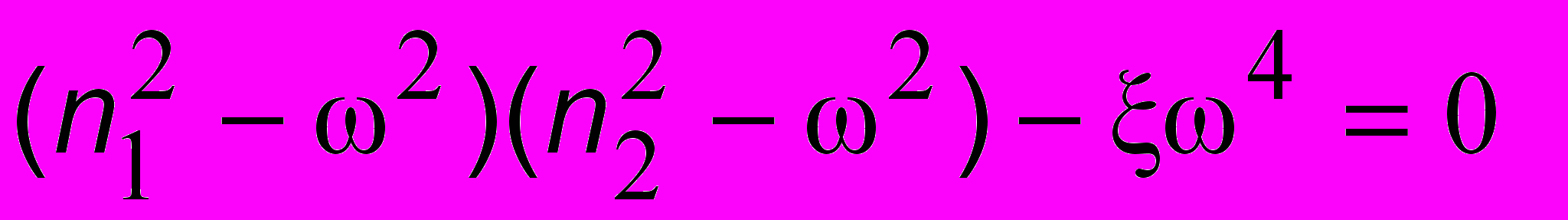и далее

,

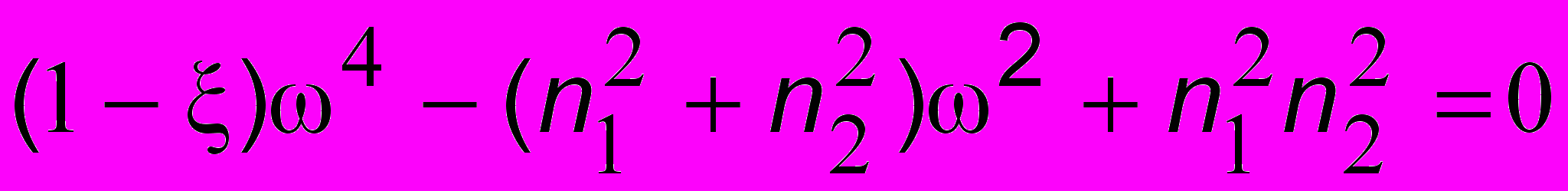т.е. биквадратное уравнение, где введено обозначение   M2/(L1L2). Это так называемый коэффициент связи систем. Если он равен нулю (при М = 0), то контуры ведут себя как независимые друг от друга осцилляторы. Решение биквадратного уравнения имеет вид:


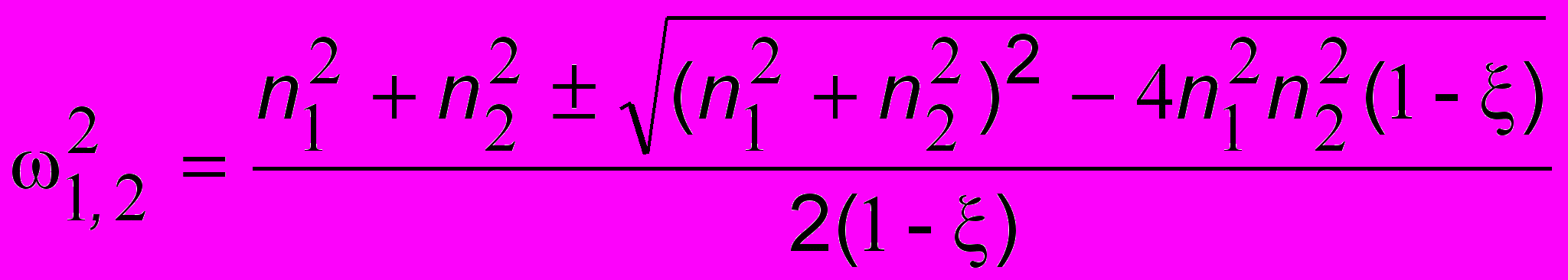. (8.3)


Отсюда получаются два положительных1 значения круговой собственной частоты гармонических колебаний системы 1 и 2, которые не равны парциальным частотам n1 и n2. Из (8.3) видно также, что всегда 1 < n 1, 2 < 2: парциальные частоты всегда расположены между собственными. При   0 из (8.3) получим 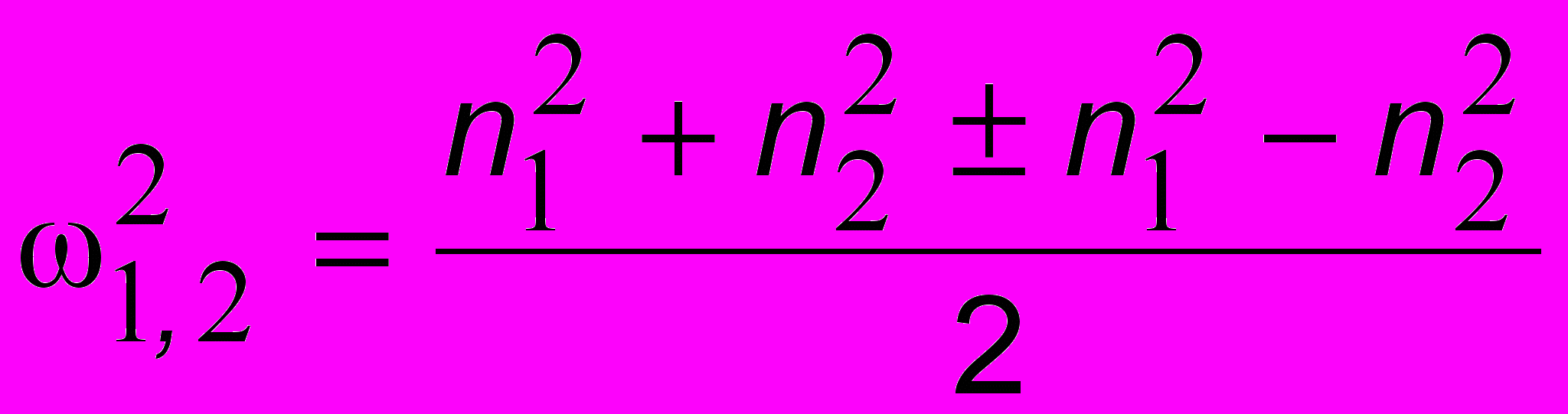, откуда следует что 1n1 и 2n2 , чего и следовало ожидать: при разъединении контуров собственные частоты стремятся к парциальным. Подставив 1 и соответствующие этой собственной частоте константы А1 и В1 в (8.2), получим отношение двух амплитуд частоты 1: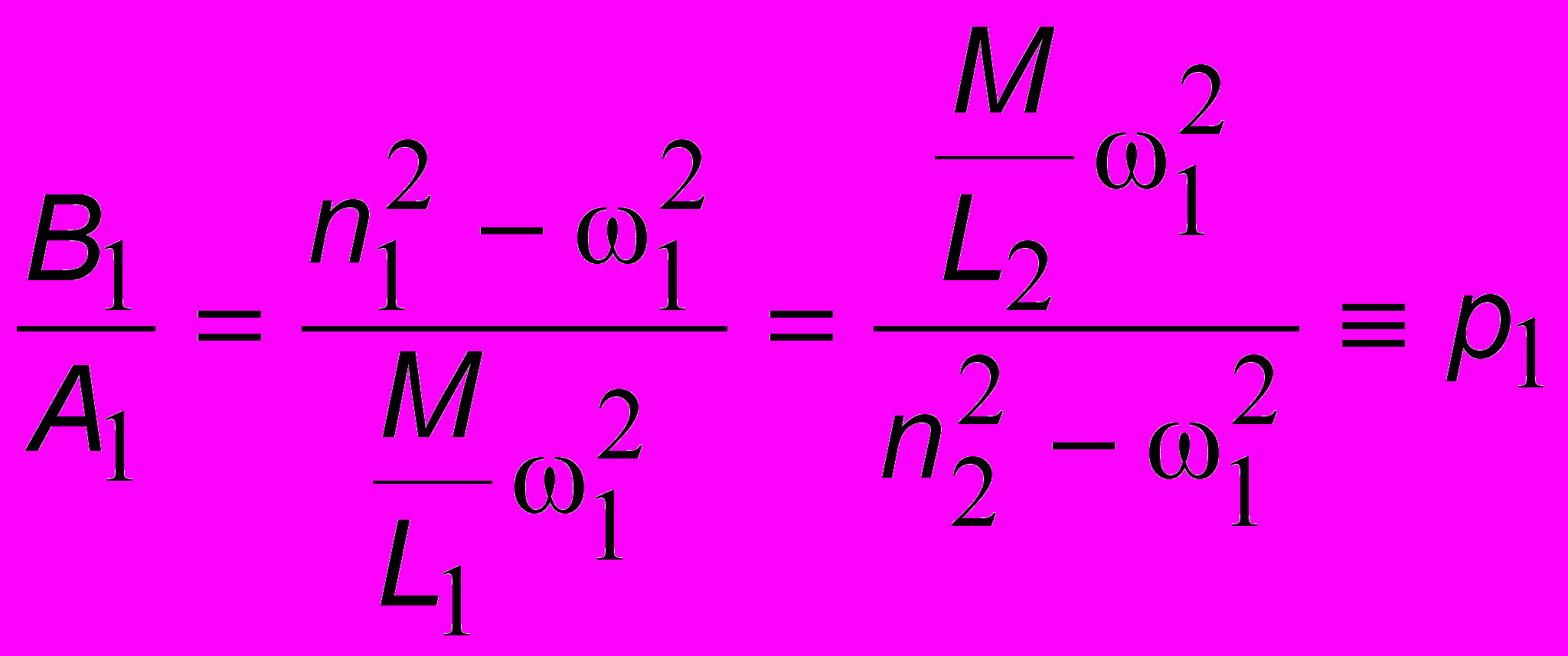



Следовательно, амплитуда колебаний частоты 1 в одном контуре может быть произвольной, но амплитуда колебаний этой же частоты в другом контуре - величина вполне определенная. Аналогично имеем:

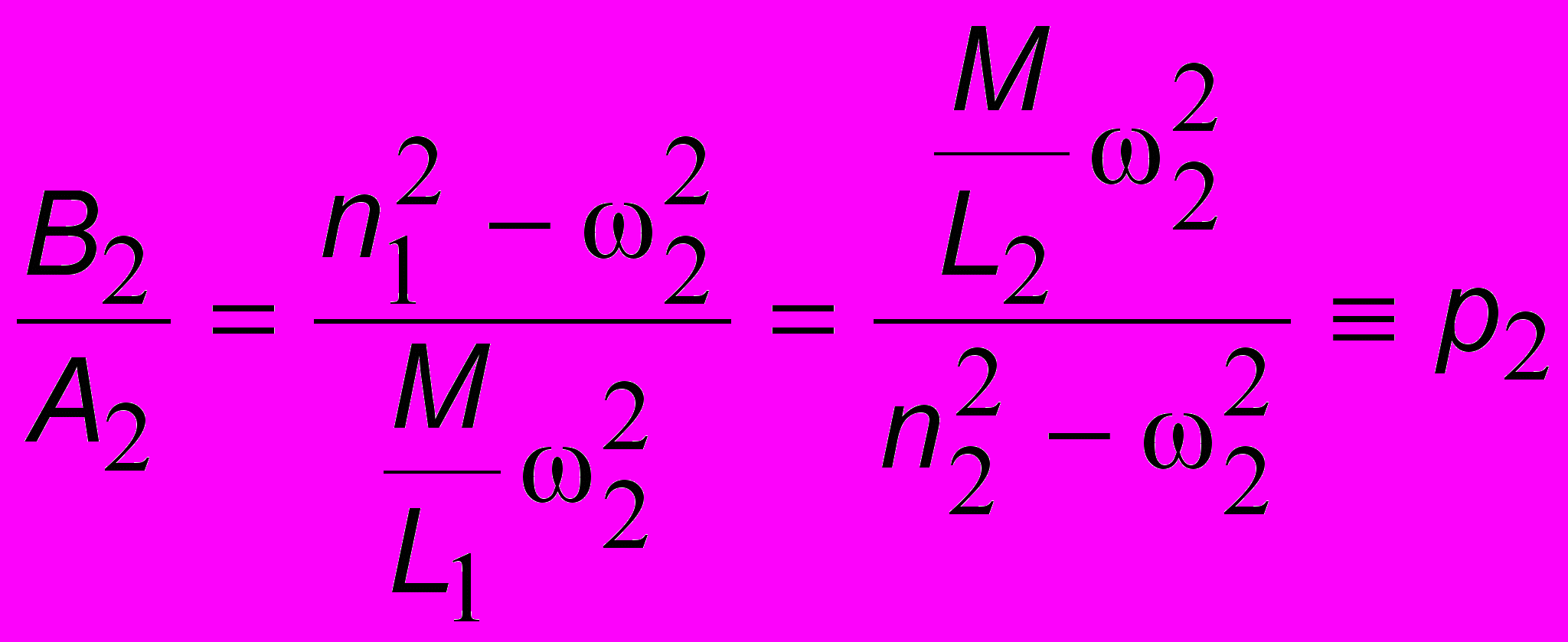и тогда B1 = p1A1, a B2 = p2A2. Таким образом, общее решение исходной системы имеет следующий вид:


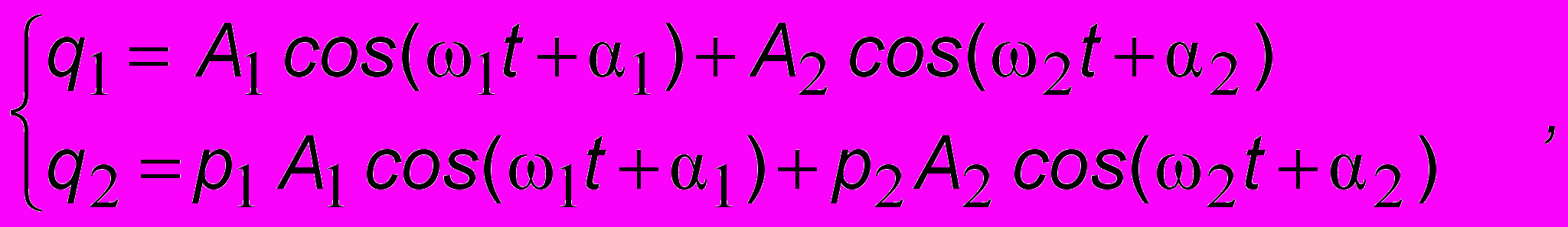(8.4)


где A1, A2, 1, 2 - константы, определяемые начальными условиями (начальным зарядом и начальным током в каждом контуре).

В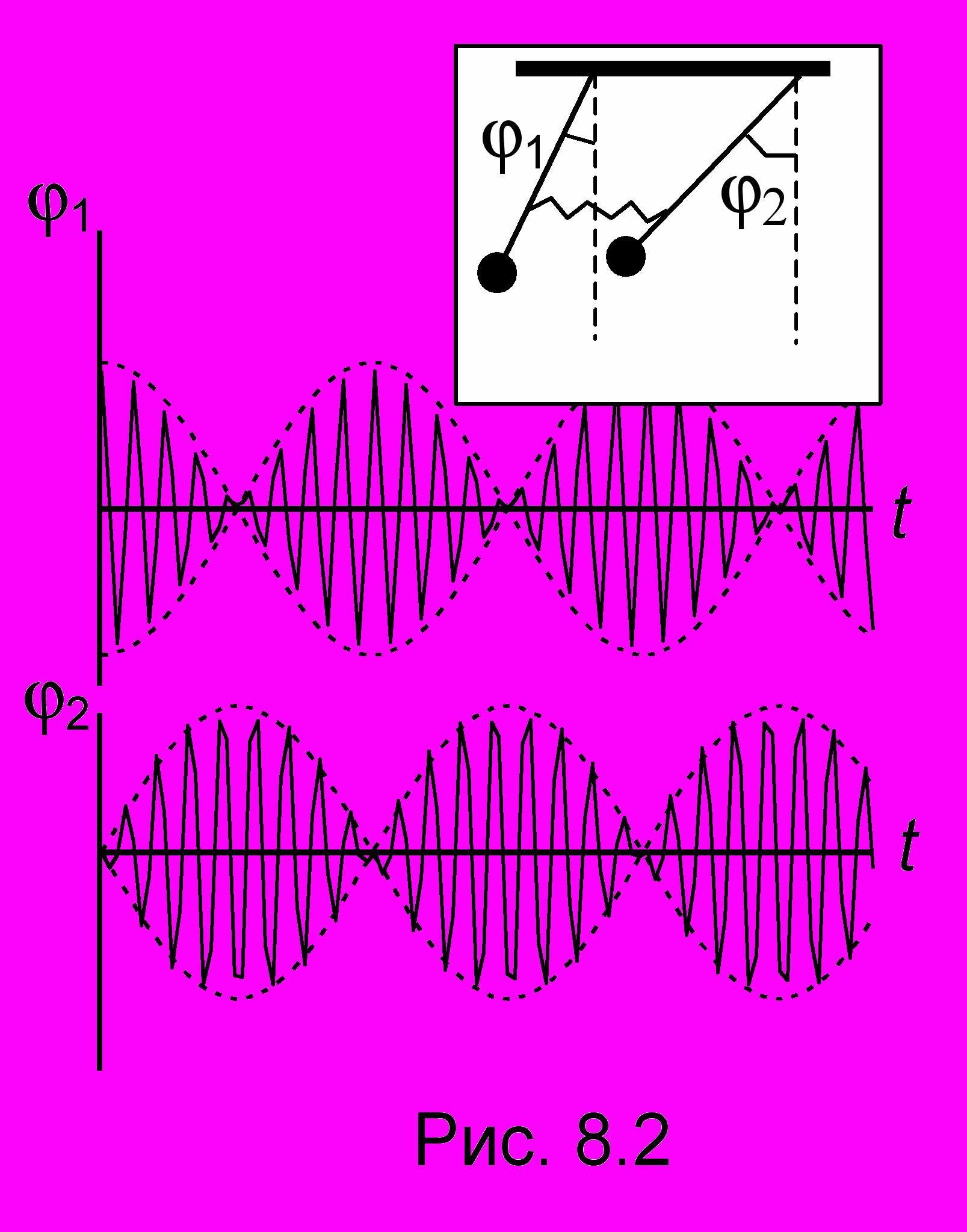идно из (8.4), что в каждом контуре колебания состоят из двух частот, и нельзя сделать так, чтобы в первом контуре колебания имели частоту 1­, а во втором 2. Можно однако сделать, чтобы вся система колебалась с частотой 1 (это будет, если А2 положить равным нулю) или с частотой 2 (если положить А1 = 0). Это - так называемые нормальные колебания (или нормальные частоты). Их получение легко проиллюстрировать на сходной механической системе, состоящей из двух связанных пружиной маятников (см. рис. 4.2). Если маятники развести в противоположные стороны и затем отпустить, то система будет колебаться с одной из нормальных частот. Если же оба маятника отклонить в одну сторону и отпустить - то с другой. В общем же случае колебания не будут гармоническими, и если 1  2 , то получим биения. На рис. 8.2 показан случай, когда из двух связанных маятников отклонили один (например, левый отклонили влево) и отпустили, а другой оставили в покое. Угловая координата 1 первого маятника при t = 0 имеет максимальное значение и затем начинает убывать. Одновременно из нулевого положения (2= 0) начинает раскачиваться второй маятник. Как видно из рисунка, при полной остановке первого маятника (1= 0) раскачка второго маятника максимальна. Затем начнут убывать амплитуды второго маятника и соответственно нарастать амплитуды первого до полной остановки второго и т.д.

Рассмотрим теперь вынужденные колебания в механической системе с двумя степенями свободы на примере важной инженерной модели. Пусть имеется консольная балка (рис. 8.3) с установленным на ней электромотором, номинальная частота вращения которого
N (об/с) соответствует круговой частоте (угловой скорости)  = 2N . С этой частотой мотор действует на балку, заставляя её колебаться.

С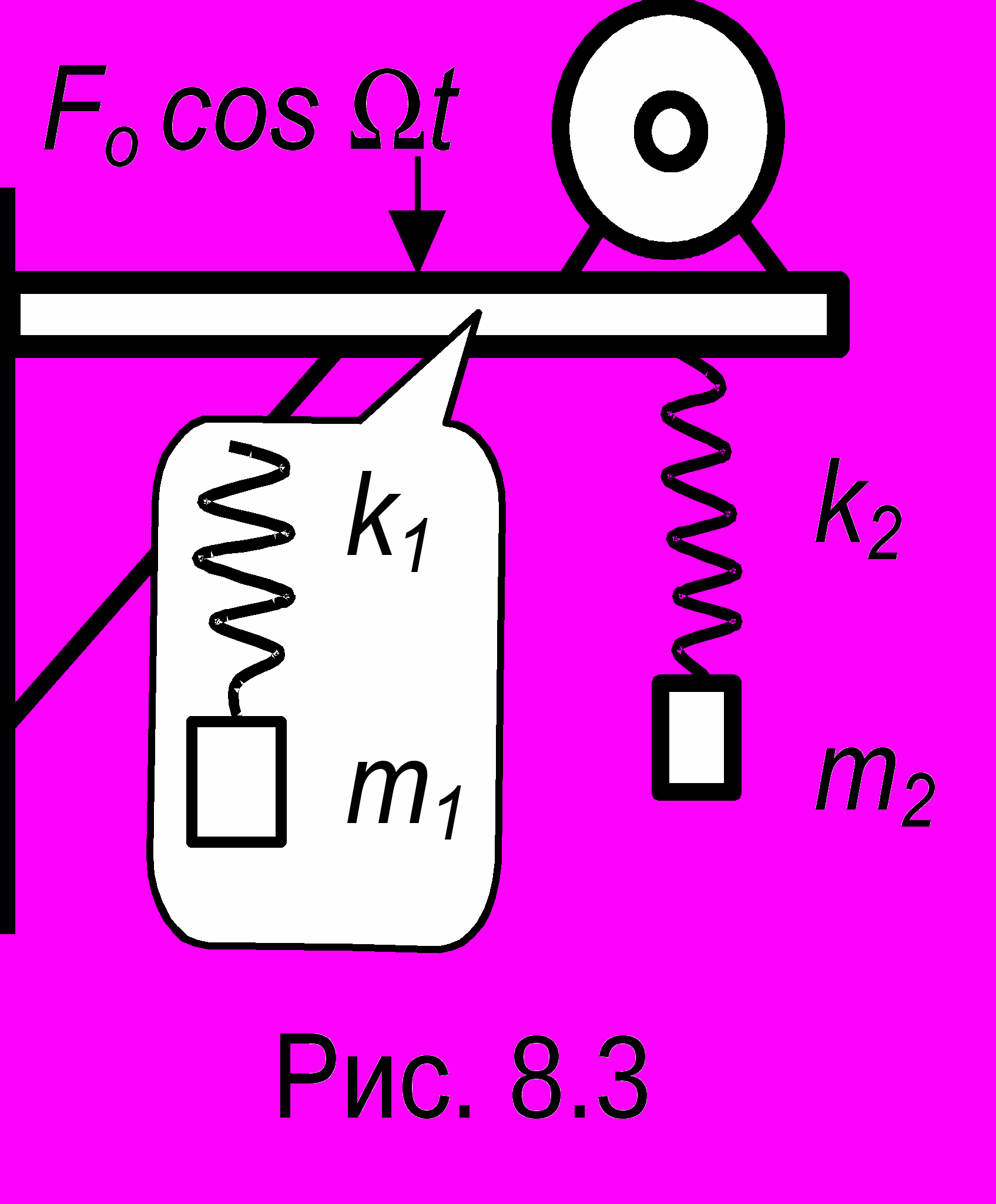ама балка эквивалентна пружинному маятнику с параметрами k1, m1 (см. выноску на рис. 8.3) и если частота мотора близка к собственной частоте балки (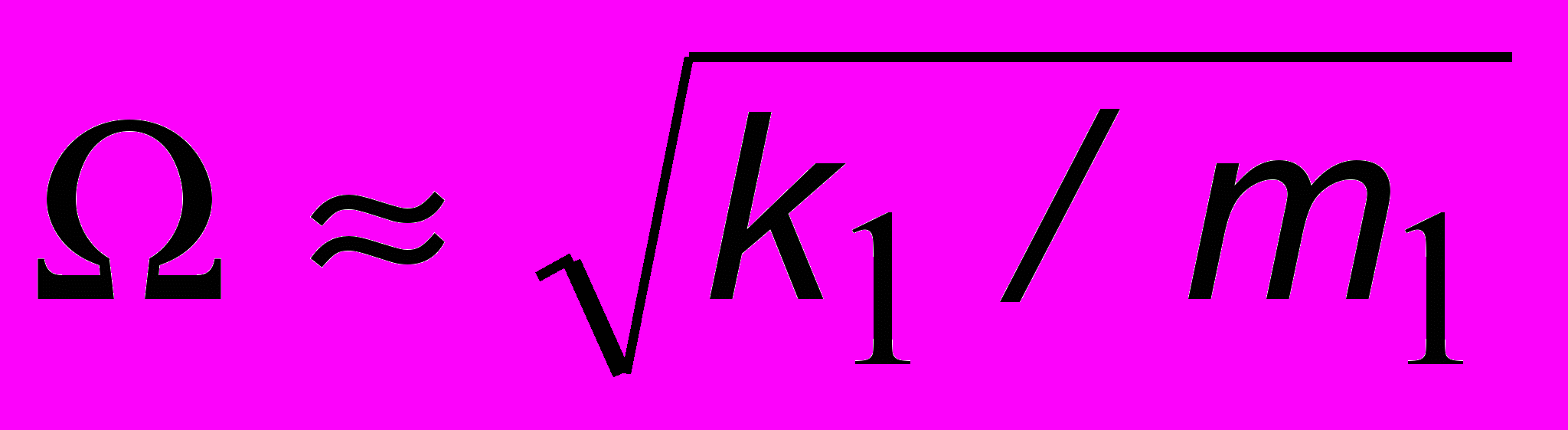), то возникает опасность разрушительного резонанса. Если к балке подвесить пружинный маятник (k2, m2), называемый демпфером, то в новой системе с двумя степенями свободы ситуация коренным образом изменится. На рисунке 8.4 показана зависимость амплитуды а1 колебаний балки без демпфера (пунктир) и с демпфером (сплошная линия). Как видно из рисунка, двугорбая кривая для системы с демпфером проходит через нуль при  = n2, а амплитуда колебаний балки на "опасной" частоте  = n1 становится незначительной.

Т
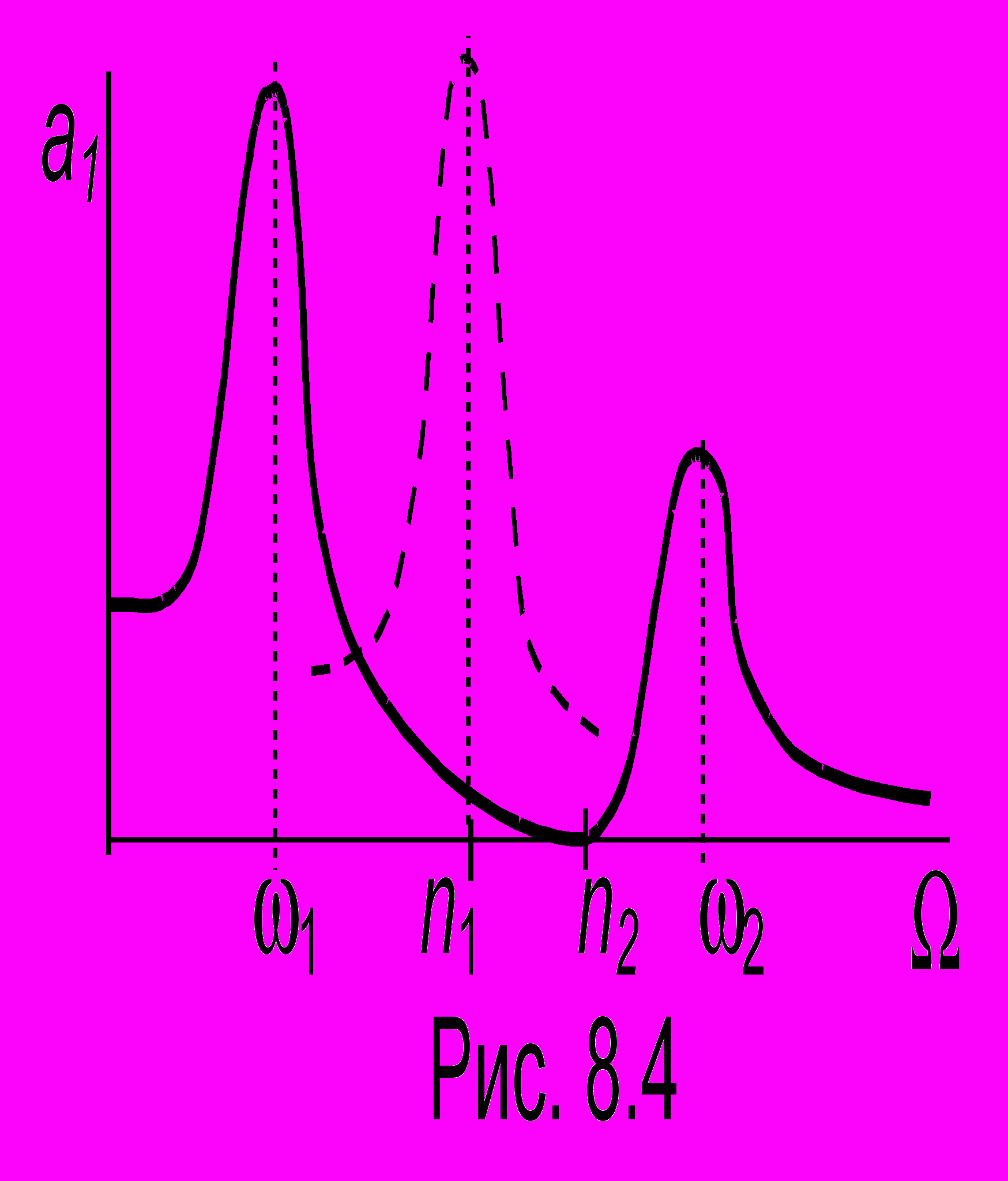
аким образом, если к балке подвесить пружинный маятник, то резонанс в системе на частоте n1 возбуждаться не будет.

Подобные системы широко используются в инженерной практике для подавления нежелательных колебаний, например, в системах амортизаторов и рессор в подвесках автомобилей.

1 Отрицательные частоты не имеют физического смысла