И в авторской редакции. Удк 536. 7 +"7"+ (201) +53+57 +577. 4+211 Вейник А. И., «Термодинамика реальных процессов», Мн.: "Навука I тэхнiка", 1991. 576 с. Isbn 5-343-00837. Вмонографии приводятся ряд новых закон
| Вид материала | Закон |
Содержание2. Простое метрическое явление. V . При таком подходе сжатие газа поршнем сопровождается повышением давления, но уменьшением объема V |
- Впервые в авторской редакции, 9591.86kb.
- Конспект лекций Кемерово 2004 удк: 637. 992, 2553.59kb.
- Хавронюк Микола Іванович удк 343 (4: 447) Кримінальне закон, 3077.54kb.
- М. М. Ничипорчук национальный исследовательский ядерный университет «мифи» моделирование, 9.59kb.
- Удк [544. 77: 577. 112. 824]: 535, 64.03kb.
- Хавронюк Микола Іванович удк 343 (4: 447) кримінальне закон, 684.97kb.
- Учебное пособие и Учебный словарь-минимум по религиоведению. М.: Гардарики, 2000. 536, 8576.03kb.
- Учебное пособие и Учебный словарь-минимум по религиоведению. М.: Гардарики, 2000. 536, 8588.39kb.
- И. А. Бунин принадлежал к тем реалистам рубежа веков, которым была дорога сущность, 164.9kb.
- Формирование гендерного подхода к обучению и воспитанию учащихся в школе 343, 102kb.
2. Простое метрическое явление.
Вторым по важности следует признать истинно простое метрическое явление (от греческого metron – мера, размер), которое так же, как и хрональное, крайне интересует всех: и обывателя, и инженера, и философа, и ученого, но которое еще не получило должной качественной и количественной расшифровки.
Согласно парадигме ОТ, все сущее состоит из вещества и его поведения. Следовательно, пространство тоже должно быть отнесено к одной из двух указанных категорий. К какой именно – это легко видеть из правила аддитивности: пространство способно суммироваться, следовательно, оно является веществом, а не поведением, причем простым веществом, ибо его не удается разложить на более простые составляющие.
Установив таким образом факт существования вещества-пространства, мы тем самым должны приписать ему все те общие свойства, которыми обладает любое вещество. Следовательно, пространство есть объективная реальность, оно абсолютно – в этом заключаются главные общие свойства пространства.
Вместе с тем пространство обладает и многими частными, специфическими, неповторимыми свойствами, присущими только ему одному. Главным из них служит свойство протяженности. Этим свойством пространство наделяет все ансамбли, в состав которых входит. Благодаря наличию этого свойства мы не можем сказать, что метрическое вещество заполняет некое вместилище, например некое пустое пространство, наподобие пустого ящика без стенок, ибо пустого пространства в природе нет и не может быть. Пустое пространство равносильно пустому веществу, то есть отсутствию вещества, а отсутствие пространственного вещества есть отсутствие самого пространства. Следовательно, имеется только вещественное пространство, вне этого вещества не может быть и свойства протяженности. Все остальные вещества природы, включая хрональное, существуют "параллельно" с пространством, но внутри него, как бы "размазаны" в нем. Специфическим свойством протяженности они не обладают, ибо это свойство есть прерогатива одного лишь пространства.
Другое важнейшее специфическое свойство метрического вещества, являющееся следствием протяженности, заключается в том, что в пространстве все располагается "в смысле порядка положения" (Ньютон). Это значит, что в данной точке пространства не могут одновременно находиться две порции метрического вещества. Одна порция может попасть в эту точку только путем вытеснения из нее второй порции. В противоположность этому в данной точке пространства может находиться любое число порций всех остальных простых веществ, ибо они не обладают свойством протяженности.
Наконец, отсюда непосредственно вытекает еще третье важнейшее специфическое свойство метрического вещества. Суть его сводится к тому, что взаимное вытеснение, замещение различных порций возможно только в том случае, если ансамбли, содержащие метрическое вещество, обладают способностью перемещаться, двигаться друг относительно друга.
Таковы главные общие и специфические свойства пространства. Помимо главных оно обладает также многочисленными другими общими и специфическими свойствами, которые, однако, не столь кардинальны, как упомянутые, они выясняются по мере дальнейшего развития аппарата ОТ.
Мерой количества метрического вещества (пространства), или метрическим экстенсором, служит метриор Емет . Метрические интенсиал, или метриал Рмет , характеризует качество поведения метрического вещества. Согласно правилу (42), работа метрического вещества, равная изменению энергии системы, определяется по формуле
dQмет = Рмет dЕмет = dU (238)
Необходимо теперь вложить конкретный физический смысл в понятие метриора, а затем и метриала.
Поскольку главное специфическое свойство пространства – это протяженность и поскольку мы живем в трехмерном мире, постольку сразу же возникает идея о том, чтобы в качестве меры количества метрического вещества выбрать некий объем. Однако объем мы привыкли измерять с помощью линейного размера, взятого в третьей степени. Очевидно, сто такая сложная конструкция, не удовлетворяющая важнейшему требованию специфичности, не может служить экстенсором. Тем более что линейный размер – это экстенсор условно простого перемещательного явления, не обеспеченного своим специфическим веществом (см. параграф 5 гл. XV). Аналогично и сам объем выступает в роли экстенсора условно простого механического явления (см. параграф 4 гл. XV). О других, более существенных недостатках объема как экстенсора для истинно простого метрического явления говорится ниже. Следовательно, объем в обычном его понимании отпадает.
Для определения физического смысла метриора придется обратиться к третьему важнейшему специфическому свойству пространственного вещества, оно вытекает из второго, заключающегося в существовании порядка положения. Чтобы соблюдать порядок положения, тела должны перемещаться, двигаться, только таким способом они могут вытеснять друг друга со своих мест. Благодаря этому в рассмотрение естественно вовлекается классическая механика с ее обширным кругом блестяще отшлифованных понятий и законов. Среди этих понятий нас в первую очередь должно интересовать то, что является мерой количества вещества применительно к перемещению, движению. Известно, что такой мерой служит масса m, измеряемая в килограммах.
Это понятие сложилось не сразу. Оно формировалось в течение нескольких поколений, начиная с Аристотеля и Герона и вплоть до Коперника, Гильберта, Кеплера. Непосредственные предшественники Ньютона (Декарт и Гюйгенс) еще путали понятия количества вещества и веса. Четко различил из Бальяни в 1638 г. Но дальше всех пошел Ньютон в своих "Началах", он массу определил как меру "количества материи" и успешно применил ее в своих законах механики [53, с.129].
Масса хорошо описывает третье важнейшее свойство метрического вещества – перемещение, движение. Ниже мы убедимся, что она пригодна также для полного определения двух первых главных свойств этого вещества – протяженности и порядка положения. Масса удовлетворяет и требованию специфичности. Следовательно, ее вполне можно избрать на роль экстенсора истинно простого метрического явления. Разумеется, будучи мерой количества метрического вещества (метрической формы материи), масса не в состоянии охарактеризовать всю материю в целом, все ее разнородные формы.
Зная экстенсор (метриор), нетрудно по изложенным выше правилам найти сопряженный с ним интенсиал (метриал). Обозначим его через , его размерность выражена в Дж/кг. В результате общая формула (238) приобретает следующий конкретный вид:
dQm = dm = dU (239)
Интересно, что в похожем виде работу и изменение энергии впервые записал У. Гиббс в 1874 г. применительно к химическим превращениям, не подозревая, что в действительности уравнение (239) имеет значительно более общее и важное значение, ибо определяет фундаментальное истинно простое метрическое явление. В условиях химических превращений используется аналогичная формула, но в ней так называемый химический потенциал имеет отличный от смысл (см. параграф 19 гл. XV).
теперь нам предстоит углубить наше понимание величин m и и обсудить способы их измерения. Это будет сделано в настоящем и нескольких следующих параграфах. Начнем с выяснения смысла меры m , заменив ее для наглядности более привычной нам характеристикой – объемом , измеряемым в м3. Тогда сопряженный с этим новым условным экстенсором интенсиал будет иметь размерность давления (Н/м2). Условная подмена массы m на объем осуществляется таким образом, что
m = k (240)
где k - коэффициент пропорциональности, величина которого зависит от единиц измерений. Этим мы как бы отождествляем массу m и объем , что позволяет о массе применительно к пространству говорить на более понятном языке – в терминах объема. При этом формула (239) приобретает вид
dQ = d = dU (241)
Здесь важно подчеркнуть, что объем ничего общего не имеет с упомянутым выше объемом V , к которому мы привыкли. Чтобы во всем этом лучше разобраться, рассмотрим механизм процесса заряжания системы объемом . Этот механизм представляет большой интерес, так как позволяет сделать много далеко идущих выводов и прогнозов.
Согласно ОТ, пустоты в природе не существует. Все, в целом непрерывное, пространство образовано метрическим веществом, обладающим свойством протяженности и состоящим из большого множества отдельных его порций, или квантов (метриантов). Это вещество может находиться либо в состоянии парена – нулевой активности, когда давление = 0, либо в активном, возбужденном состоянии, когда давление не равно нулю. В реальных условиях кванты активного пространства чередуются в каком-то порядке с квантами пассивного (парена). Поэтому если с помощью воображаемой контрольной поверхности мысленно выделить из окружающей среды некоторую систему объемом V , то в нее одновременно попадут метрианты обоих типов. Активные метрианты в составе соответствующих ансамблей образуют изучаемое тело.
На рис. 6 представлены два состояния системы, отмеченные индексами 1 и 2, причем активные метрианты изображены черными клеточками, а пассивные – светлыми. Под объемом следует понимать только совокупность объемов активных метриантов (черных клеточек). Отсюда должно быть ясно, почему надо четко различать экстенсор и суммарный контрольный объем V , а также почему объемом можно успешно подменять массу m .
Поскольку пространство непрерывно, постольку подвод к системе активных метриантов в количестве d = 2 - 1 (рис. 6, а и б) неизбежно должен сопровождаться вытеснением соответствующего количества метриантов парена (рис. 6, б, светлые клеточки). При этом концентрация активных метриантов /V возрастает, что приводит к повышению давления . Увеличение давления есть следствие взаимодействия между сближающимися ансамблями системы. Аналогичная картина наблюдается при заряжании системы любым веществом, в этом отношении метрическое не является исключением из общего правила. Например, при подводе (увеличении) электрического заряда растет потенциал системы, при подводе термического вещества – температура и т.д. Специфическое отличие метрического явления от всех остальных заключается в том, что заряжание системы объемом происходит путем замещения пассивных квантов пространства активными. У всех остальных явлений при заряжании наблюдается простой подвод активных квантов вещества на общем фоне пространства, вложение ("вмазывание") этих квантов в кванты пространства.
Посмотрим теперь, как описанный механизм выглядит применительно к поршневому двигателю. Предположим для этого, что имеется цилиндр с поршнем (рис. 6, в), заполненный газом. Под объемом будем, как и прежде, понимать совокупность активных метриантов газа, расположенных между некоторыми контрольными сечениями I и II , выделяющими в цилиндре из общего объема V1 величину V . Парен обладает всепроникающими свойствами, поэтому при движении поршня последний воздействует только на активные метрианты, число которых (концентрация) в контрольном объеме V увеличивается, а парен свободно проходит сквозь тело цилиндра и поршня (рис. 6, г). В результате газ сжимается от объема V1 до объема V2 , но при этом одновременно возрастает как объем , так и давление . При этом следует иметь в виду, что пассивных метриантов (парена) неизмеримо больше, чем активных.
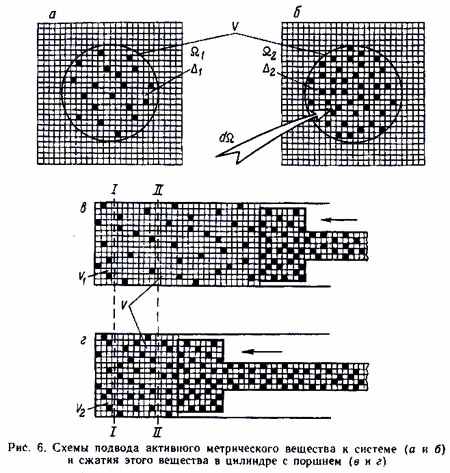
В противоположность этому в термодинамике рассматривается полный объем V . При таком подходе сжатие газа поршнем сопровождается повышением давления, но уменьшением объема V . Из-за этого работа входит в уравнение первого начала со знаком минус, чем она и отличается от работ всех остальных веществ. Причина такого отличия ранее была не ясна.
Должен признаться, что меня всегда смущало общепринятое толкование механических явлений, приводящее к формуле (43). Свой протест я очень робко выразил тем, что в книгах [13, с.29; 15, с.46] сказал об условном перетекании объема сквозь поршень. В настоящей монографии я постарался по возможности стряхнуть с себя груз традиционных представлений и последовательно оставаться на позициях ОТ. В свете новых представлений мы теперь с полным правом можем говорить о том, что в тепловом двигателе работу совершает активное метрическое вещество (активное пространство), а движущей силой указанного процесса служит давление, определяемое концентрацией этого вещества в некотором контрольном объеме.
Изложенная здесь трактовка метрического явления логически вытекает из общего строя рассуждений ОТ и ставит пространство в один ряд со всеми остальными простыми формами вещества. Это должно заметно изменить наше миропонимание. Что касается практических целей, то для инженерных расчетов из-за непривычности экстенсора и неумения пока его определять вполне допустимо пользоваться общеизвестными методами: объемом V , перемещением х и массой m , которые сопряжены с давлением р , силой Рх и квадратом скорости 2 и соответствуют условно простым механическому, перемещательному и кинетическому явлениям, вытекающим в качестве частных случаев из метрического.
Однако привлечение объема для выяснения физического смысла массы m , являющейся мерой количества метрического вещества, весьма полезно. Оно позволяет на примере процессов заряжания системы этим объемом и сжатия газа в цилиндре с поршнем лучше понять само метрическое явление, его главные свойства.
В целом истинно простое метрическое явление, как и хрональное, подчиняется всем законам ОТ. Например, переход метрического вещества через контрольную поверхность системы сопровождается совершением работы (первое начало). Количество метрического вещества, мерой которого служит масса, подчиняется закону сохранения (второе начало). Связь метрического явления со всеми остальными регулируется третьим и четвертым началами. Перенос метрического вещества происходит под действием разности метриантов (пятое и шестое начала), этот процесс сопровождается эффектами заряжания и экранирования (седьмое начало).
Как и всякое истинно простое вещество, метрическое на уровне наномира излучает соответствующее нанополе, представляющее собой вещество взаимодействия и имеющее силовые свойства. Именно метрическое нанополе ответственно за взаимодействия, которые ныне именуются гравитационными и инерционными. К этому вопросу нам придется возвращаться еще не раз.
На уровне микромира метрическое, подобно всем другим веществам, имеет дискретную, зернистую, порционную, квантовую структуру. Мера количества метрического вещества, содержащегося в одной порции, или метриант, сейчас пока неизвестна. О конфигурации и сопряжении между собой отдельных метрических порций (квантов) вещества, обусловленном их конфигурацией, говорить бессмысленно, ибо вне кванта пространства свойство протяженности отсутствует вовсе.
В макромире метрическое вещество обладает континуальными свойствами и наделяет макроскопические тела, в состав которых входит, свойствами протяженности и порядка положения, способностью перемещаться и т.д. Многие другие свойства метрического явления, особенно в его связи с хрональным, обсуждаются ниже. Здесь целесообразно сделать несколько кратких замечаний, касающихся сравнительных свойств пространства и времени.
Уже отмечалось, что время и пространство обычно принято рассматривать как некие эталоны, которые используются при сравнении различных других явлений. Этому способствовала та часть формулировок, где говорится, что время и пространство суть категории, которые не зависят ни от чего внешнего (из предыдущего должно быть ясно, что Ньютон имел ввиду эталонное, равномерно текущее время). Инженер, сильно стесненный рамками времени и пространства, прибегает к этому приему очень охотно и с большой пользой для дела. Примером может служить пятое начало ОТ, где некоторые потоки отнесены ко времени и геометрическим размерам, в частности к площади, теперь мы можем очень четко определить границы применимости этого приема.
Очевидно, что используемое инженером время может исправно выполнять свои обязанности эталона только в тех случаях, когда рассматриваются устройства с практически одинаковым ходом времени. По мере внедрения общей теории в инженерную практику будут все чаще встречаться системы с разным ходом времени. В этих условиях в уравнения переноса придется включать потоки хронального вещества либо вносить поправки на неодинаковый ход реального времени.
Что касается пространства, то оно представляет собой простое вещество и поэтому действительно не зависит ни от чего внешнего. Следовательно, оно всегда может быть использовано в качестве эталона. При этом безразлично, какое пространство имеется в виду – пассивное, активное или и то и другое вместе взятые. Для этих целей оба вида пространства совершенно равноценны, важно лишь, чтобы они использовались как непрерывная среда, континуум. Другими словами, контрольные объем, поверхность или линия должны быть мысленно выделены или проведены в пространстве через пассивные и активные его области одновременно, без разрывов. Например, на рис. 6 контрольный объем V охватывает парен и активное пространство, не отдавая предпочтения ни одному из них. В данном случае равноценность пассивных и активных квантов говорит о том, что мы вполне можем вторые мысленно подменить первыми. А это значит, что контрольный объем есть характеристика абсолютная, ни от чего не зависящая, ибо она фиксируется как бы относительно неподвижного парена, который представляет собой абсолютную систему отсчета (см. параграф 5 гл. XVII).
Следовательно, объем V является единственной абсолютной макроскопической характеристикой, связанной с пареном и одновременно поддающейся непосредственному и весьма точному измерению. Измерения возможны благодаря тому, что кванты невидимого метрического вещества парена перемежаются квантами видимого (активного), и об объеме мы фактически судим по расположению видимых квантов. Например, суммарный объем V цилиндра на рис. 6, в равен V1 , а на рис. 6, г – V2 ; эти величины фиксируются по газу, но они включают в себя одновременно метрианты как газа, так и парена. Все это делает объем V идеальным эталоном, к которому целесообразно относить соответствующие характеристики системы.
Этот вывод имеет важное значение, так как на практике обычно принято различные характеристики относить не к единице объема V , а к единице массы системы, например удельный объем, удельная массовая теплоемкость и т.д. Однако в свете изложенного становится ясно, что подобный прием не очень удачен.
Действительно, согласно третьему началу ОТ, свойства системы определяются количествами заключенных в ней различных простых веществ, то есть фактически концентрацией этих веществ во всем объеме V , а не только в объеме , пропорциональном массе m . Это легко понять, если вспомнить, что концентрация определяет расстояния между взаимодействующими частицами; расстояния, в свою очередь, характеризуют интенсивность взаимодействий, а значит, и свойства. Следовательно, относя характеристики системы к единице массы (объема ), мы тем самым упускаем из виду влияние концентраций веществ в остальном ее объеме V - : при равных массах эти разные, не учитываемые в объеме V - концентрации дадут неодинаковые удельные свойства, что может привести и зачастую приводит к неправильным выводам. Это хорошо продемонстрировано в работе П.Н. Кобзаря [49].
Особого внимания заслуживают идеи Ньютона о порядке последовательности и порядке положения. При этом уместно обратить внимание на одну тонкость, которая касается разницы между этими двумя порядками. Суть дела заключается в том, что реальное время определяет хрональный интенсиал, или хронал, а пространство есть вещество, мерой количества которого служит метрический экстенсор, или метриор. Это наделяет порядок последовательности и порядок положения определенными принципиально различными свойствами. Порядок положения имеет ту особенность, что в данной точке пространства одновременно может находиться только один метриант, принадлежащий некоторому телу. Другой метриант, принадлежащий второму телу, может попасть в эту точку лишь методом вытеснения, замещения.
Что касается порядка последовательности, то хронал и ход времени могут иметь одинаковые значения у любого числа различных тел. Это значит, что в данной временной точке одновременно могут находиться многие тела. Однако если мы находимся на одном теле, а на втором ход времени ускорился, тогда мы будем видеть его будущее, а если замедлился, - то его прошлое в сравнении с нами. Обратная картина получается, если мы ускоряем или замедляем ход времени на своем теле, например, в каюте какого-либо устройства. Все это вносит в проблему порядка последовательности известную специфику и может быть положено в основу построения соответствующих "машин времени".
Разумеется, о порядках последовательности и положения можно говорить применительно к телам, содержащим хрональное и метрическое вещества. Вне этих веществ не может существовать ни порядка последовательности, ни порядка положения. Иными словами, без хронального вещества тело существует вне времени, без метрического – вне пространства. Вневременность означает нескрепленность с хрональным веществом, независимость от времени, неподвластность времени, "размазанность" по времени. Внепространственность надо понимать как нескрепленность с пространством, независимость от него, существование параллельно, внутри пространства, "размазанность" по его объему, как отсутствие у тела свойств протяженности, размеров и массы и, вероятно, как вездесущность.
В связи с этим возникает естественный вопрос, возможны ли в природе вневременные и внепространственные системы? А почему бы и нет? Ведь есть же ансамбли, которые не имеют в своем составе определенных квантов, например квантов электрического вещества; в частности, подобным свойством обладает фотон. Точно так же могут быть и ансамбли, не содержащие квантов хронального вещества, либо пространства, либо того и другого одновременно. В принципе все это легко себе представить, да и опыт говорит о том же (см. гл. XXVI). Такие ансамбли будут существовать вне времени и пространства, свойствами длительности и протяженности они обладать не будут, для них понятия порядка последовательности и порядка положения не имеют никакого смысла. Отсутствие протяженности делает соответствующие тела всепроницаемыми, а отсутствие массы устраняет запреты механики на слишком большие скорости и ускорения. Иными словами, вырисовывается возможность существования более тонких миров, чем наш, отличающихся экзотичностью свойств; нечто подобное в работе [21, с.24] я назвал пико-, фемто- и аттомирами. Как видим, действительность оказывается много интересней, богаче и фантастичней всех самых фантастических научно-фантастических измышлений.
Наконец, становятся понятными слова Ньютона о том, что "время и пространство составляют как бы вместилища самих себя и всего существующего", ибо вне метрического вещества нет пространства, а вне хронального вещества – времени; при этом все остальные простые вещества оказываются "размазанными" внутри пространства. К тому же основное – пассивное – пространство (парен) действительно "остается всегда одинаковым и неподвижным" и служит абсолютно системой отсчета расстояний и скоростей (см. параграф 5 гл. XVII).
Я умышленно более подробно остановился на описании свойств хронального и метрического явлений, так как изложенная здесь трактовка сильно отличается от привычной, где время и пространство выделяются в особые категории, стоящие в стороне (над) от всех остальных явлений. Из сказанного должно быть ясно, что время и пространство суть весьма частные категории, имеющие к тому же существенно различный ранг. Поэтому они в принципе не в состоянии содержать в себе на правах ящиков без стенок всю Вселенную. И их нельзя ни суммировать, ни заставить подменять друг друга. При этом особый теоретический и практический интерес должны представлять бесхрональные и безметрические тела и объекты, "размазанные" по времени и пространству [ТРП, стр.244-254].
