Лекция 1 Введение

Вид материала

Лекция

Содержание Классификация систем по степени противоречия целей Системный подход Системный подход к управлению Что имеем а базе? Вариант системного подхода Структурные математические модели В топологических Основные классы экономико-математических моделей Экономико-математическая модель, как правило, включает три основные составные части Управляемые переменные Возможные исходы (отклики) Процесс моделирования Расширение модели Оценка адекватности Необходимые термины и понятия из теории управления Где нет выбора, там нет и не может быть управления. Иерархические системы управления. Таблица 1. Шкала спроса одного покупателя на мясо за месяц Закон спроса Эффект дохода ... Полное содержание

Подобный материал:

• С. В. Шадрина Лекция 5 сентября, 15: 00-16: 30, Введение в геометрию пространства модулей, 5.97kb.
• Первая лекция. Введение 6 Вторая лекция, 30.95kb.
• Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
• А. И. Мицкевич Догматика Оглавление Введение Лекция, 2083.65kb.
• Лекция введение в экологию (В. И. Торшин), 1146.79kb.
• Конспект лекций н. О. Воскресенская Москва 2008 Оглавление: Лекция Введение в дисциплину, 567.5kb.
• План лекций педиатрический факультет 1 семестр 1 лекция. Введение в анатомию человека., 216.63kb.
• Сидоров Сергей Владимирович Планы лекций Введение в профессионально-педагогическую, 19.81kb.
• Русской Православной Церкви и их особенности. 22 сентября лекция, 30.24kb.
• План лекций: Лекция №1. Введение в тему, общие сведения. Введение, 99.54kb.

Подсистемой будем называть выделенное из систем подмножество взаимосвязанных элементов,

объединенных некоторым целевым назначением.

Любая система может быть представлена как композиция (объединение) подсистем различных уровней и

рангов.

Декомпозиция как (разделение) системы на подсистемы может быть проведена по определенным

признакам различными способами.

Деление системы на подсистемы по уровням и рангам называют иерархией.

При делении число уровней и количество подсистем каждом уровне зависит от конкретной системы и не

должно оговариваться заранее, однако требуется, чтобы подсистемы, входящие в данную систему, при

совместном функционировании выполняли все функции системы.

Иерархическая система управления данного уровня подчиняется системе более высокого уровня, в состав

которой она входит.

Структурой (от лат. structura — строение, расположение порядок, взаимосвязь составных частей) называется относительно постоянный порядок внутренних пространственно-временных связей системы между ее элементами и взаимодействия их с внешней средой, определяющей функциональное назначение системы.

Связи системы подразделяют на внешние и внутренние, Связи с подчиненными подсистемами или между ними считаются внутренними, а связи₎ выходящие за границы системы, — внешними. Связи обладают направленностью, Для информационных систем — это получение информации, приказа, или, наоборот, выдача информации. Связь от внешней среды к системе (или ее элементу) называется входом, а направленная вовне — выходом. Каждая связь между элементами системы является входом для одного из них и выходом — для другого.

Классификация систем

По степени сложности структуры выделяют простые и сложные системы, иногда в отдельный класс

сводят так называемые «большие» системы — совокупность разнородных сложных систем со

сравнительно слабыми связями между ними.

Характеристики «сложности» систем многообразны и сопровождаются одновременно многими

специфическими чертами, такими, как:

• многокомпонентность системы (большое число элементов, связей, большие объемы циркулирующей
  информации, др.);
  
• многообразие возможных форм связей элементов (разнородность структур древовидных,
  иерархических, др);
  
• многокритериальность, т.е. наличие ряда разноплановых (в том числе противоречивых) критериев;
  многообразие природы элементов, составляющих систему;
  

• высокий динамизм поведения системы и ее структурных характеристик и др.
  

По сложности поведения выделяются следующие типы конкретных систем:

• автоматические системы, которые могут реагировать на внешние воздействия только
  детерминировано, например, часы.
  
• решающие системы, которым присущ акт решения; они имеют постоянные стохастические критерии
  различения случайных сигналов. Примерами могут служить радиолокационная станция, рецепторные
  механизмы организмов;
  
• самоорганизующиеся системы имеют гибкие критерии различения сигналов и гибкие реакции на воз­
  действия, приспосабливающиеся к заранее неизвестным сигналам и воздействиям. Примеры —
  простейшие организмы и некоторые кибернетические системы.
  
• предвидящие системы имеют столь высокоорганизованную структуру и большие объемы
  запоминающих устройств, что сложность их поведения превосходит сложность внешних
  нецеленаправленных воздействий. Такие системы могут изучать исходы взаимодействий до данного
  момента и на основе этого изучения «предвидеть» дальнейший ход событий. (Например — человек.)
  

Классификация систем по степени противоречия целей связана с рассмотрением взаимодействия системы и внешней среды. Если рассматривать среду как некоторую систему В, то возможны три случая:

1. цель системы В такова, что она в той или иной степени способствует достижению цели системы А;
   
2. цель системы В такова, что она в той или иной степени препятствует системе А в достижении ее цели;
   
3. система В индифферентна по отношению к системе А.
   

Системный подход

Локальным решениям, полученным на основе охвата небольшого числа существенных факторов, кибернетика противопоставляет системный подход.

Традиционный подход: предусматривает расчленение изучаемого объекта на составные элементы и определение поведения сложного объекта как результата объединения свойств входящих в него систем. Системный подход ориентирует исследование на:

• раскрытие целостности объекта и обеспечивающих его механизмов; Этот принцип исходит из того,
  что целое обладает такими качествами, которые не обладает ни одна из его частей
  
• выявление многообразных типов связей сложного объекта;
  
• сведение этих связей в единую теоретическую картину.
  

Системный подход реализует представление сложного объекта в виде иерархической системы

взаимосвязанных моделей, позволяющих фиксировать целостные свойства объекта, его структуру и

динамику.

Системный подход требует рассмотрения изучаемого явления или процесса не только как самостоятельной

системы, но и как подсистемы некоторой суперсистемы более высокого уровня; прослеживания как можно

большего числа связей, не только внутренних, но и внешних — с тем, чтобы не упустить действительно

существенные связи и факторы и оценить их эффекты.

Любой объект исследования, таким образом, может быть представлен и как подсистема некоторой системы

более высокого ранга — это приводит к проблеме выделения системы, установления ее границ, — и как

система по отношению к некоторой совокупности подсистем более низкого ранга, которые, в свою очередь,

образованы некоторыми элементами, дальнейшее дробление которых нецелесообразно с точки зрения

конкретного исследования, — это определяет необходимость постановки задачи выбора такого первичного

элемента. Элементы выступают модулями структуры, «черными ящиками», внутренняя структура которых

не является предметом исследования.

В процессе анализа и синтеза систем исследуются лишь существенные связи, а прочими пренебрегают

либо интерпретируют их как возмущения, или «шум».

Системный подход, основанный на принципе целостности, в исследовании свойств объекта как единого

целого, требует непрерывной интеграции представлений о системе на каждом этапе исследования —

системного анализа, системного проектирования, системной оптимизации.

Общие принципы исследования:

• принцип максимума эффективности проектируемой и функционирующей системы;
  
• принцип субоптимизации — согласования локальных критериев между собой и с общим глобальным
  критерием функционирования системы;
  
• принцип декомпозиции, осуществляемый с учетом требования максимума эффективности. В
  результате декомпозиции может быть получена некоторая многоуровневая структура системы
  или процесса ее исследования.
  

Системный подход к управлению характеризуется одновременным комплексным всесторонним рассмотрением объекта изучения, будь то процесс, явление изделие, факт или информация. При этом изучаемое понятие представляется в виде следующей неразрывной триады, свойственной кибернетике:

S S ( 1 1 1 1 ~-	Вход	W			Выход
		,'с		s
	*		Обратная связь t \
		'-		\
	Что имеем а базе?		'Как этого достичь?	\ 1 Что мы хотим \ \ _| i — "•' получать | 1_ в результате? \

В рамках системного подхода руководители должны рассматривать организацию как совокупность взаимозависимых элементов, таких, как люди, структура, задачи и технология, которые ориентированы на достижение различных целей в условиях меняющейся внешней среды. В приложении к действующей кампании три вышеприведенные блока имеют следующую интерпретацию:

Поставщики Ресурсы Сред»		Технология Условия труда Режим работы	w	Потребитель Готовая про,оукция (товары, услуги) Режим работы
t

Вариант системного подхода

Моделирование объектов и систем

Решение проблем управления показывает, что основным фактором успешного исхода является научно обоснованная формализация задачи. Такая формализация успешно осуществляется на основе математического моделирования, которое является неотъемлемой концептуальной частью науки управления, успешно реализуемой в рамках экономической киберенетики.

Создание моделей реальных бизнес-проектов и объектов управления является квинтэссенцией кибернетического подхода к решению задач оптимизации социально-экономических систем. Здесь моделирование играет роль, аналогичную лабораторному эксперименту в естественных науках. Это тем более важно, что осуществление реального эксперимента в социуме может слишком дорого обходиться как в материальной, так и в социальной сфере.

Построение модели помогает привести сложные и подчас непреодолимые факторы, связанные с проблемой принятия решения, в логически стройную схему, доступную для детального анализа. Такая модель позволяет выявить альтернативы решения задачи и оценить результаты, к которым они приводят, а также дает возможность определить, какие данные необходимы для оценки имеющихся альтернатив. В итоге это обеспечивает получение обоснованных выводов. Коротко говоря, модель является средством формирования четкого представления о действительности.

Итак, математическое моделирование - процесс создания модели и оперирование ею с целью получения требуемых сведений о реальном объекте.

Требования предъявляемые к математическим моделям:

1. Универсальность: степень универсальности характеризует полноту отображения в модели свойств
реального объекта.

2. Адекватность: способность отображать заданные свойства объекта с допустимой погрешностью.
Оценивается с использованием понятий изоморфизм и гомоморфизм.

Изоморфизм. В строго математическом смысле изоморфизм двух систем: Si: Xi-> Yi, 82: Х?-> Y2 означает, что между входами и выходами обеих систем существует взаимно однозначное соответствие. Понятие изоморфизма систем распространяется и на структурные, и на поведенческие характеристики систем. Пример: изоморфны местность и географическая карта, объект съемки и фотография и т.д. Наличие изоморфизма между системой-оригиналом и системой-моделью характеризует весьма высокую степень адекватности, обеспечение которой при построении модели сопряжено с большими трудностями и, вообще говоря, не является необходимым. Важным частным случаем соотношения «оригинал-модель» является отношение гомоморфизма, при котором между системами Si и Sa существует однозначное пря­мое и неоднозначно-обратное соответствие. Так, модель, полученная из реальной системы путем ее упрощения (например, за счет уменьшения числа переменных путем их объединения) является гомоморфной моделью.

3. Экономичность математической модели: характеризуется затратами вычислительных ресурсов
(затратами машинного времени и памяти) на ее реализацию.

Лекция 3

Классификация математических моделей

Основные признаки классификации и типы математических моделей, которые могут использоваться в задачах менеджмента:

Признак классификации	Математические модели
Характер отображаемых свойств объекта	Структурные; функциональные
Принадлежность к иерархическому уровню	Микроуровня; макроуровня; метауровня
Степень детализации описания внутри одного уровня	Полные; макромодели
Способ представления свойств объекта	Аналитические, алгоритмические, имитационные, семантические
Способ получения модели	Теоретические, эмпирические

Структурные математические модели предназначены для отображения структурных свойств объекта (отражают внутреннюю организацию объекта: его составные части, внутренние параметры и их связи с «входом» и «выходом») и делятся на топологические и геометрические.

В топологических моделях отображаются состав и взаимосвязи элементов объекта. Их чаще всего применяют для описания объектов, состоящих из большого числа элементов, при решении задач привязки их к определенным пространственным позициям (например, в транспортной системе) или к относительным моментам времени (например, при разработке расписаний). Топологические модели могут иметь форму графиков, таблиц (матриц) списков и т.п.

В геометрических моделях, дополнительно к сведениям о взаимном расположении элементов, содержатся сведения о форме компонентов объекта. Эти модели применяют при решении различных задач проектирования (например, зданий, парковых зон и т.п.).

Функциональные математические модели предназначены для отображения процессов (физических или информационных), протекающих в объекте при его функционировании или изготовлении. Обычно содержат алгоритмы, связывающие фазовые переменные, внутренние, внешние или выходные параметры. Функциональная модель имитирует поведение объекта так, что, задавая значения «входа» X, можно получать значения «выхода» У. Построить функциональную модель - значит отыскать оператор D, связывающий X и Y: У = D(X).

В исследованиях на народнохозяйственном уровне чаще применяются структурные или структурно-функциональные модели, поскольку для планирования и управления большое значение имеют взаимосвязи подсистем. Функциональные модели широко применяются в экономическом регулировании.

В зависимости от места в иерархии описаний математические модели делятся на микро-, макро- и

метамодели.

Макроэкономические модели описывают экономику страны как единое целое, связывая между собой

укрупненные материальные и финансовые показатели: ВНП, потребление, инвестиции, занятость, ставку

процента, денежные агрегаты и др.

Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих

экономики либо поведение отдельной такой составляющей в рыночной среде. Вследствие разнообразия типов

экономических элементов и форм их взаимодействия на рынке микроэкономическое моделирование занимает

основную часть экономико-математической теории. Основной целью микроэкономического моделирования

является анализ одновременного установления, как цен, так и количества произведенных, обмененных и

потребленных продуктов в условиях определенных институциональных структур и процессов.

По степени сложности математические модели экономических объектов и явлений подразделяются на

несколько основных типов.

К первому типу относятся функциональные модели, которые выражают прямые зависимости между

известными (экзогенными) или неизвестными (эндогенными) величинами. Необходимые для построения модели

параметры определяются на основе нормативных данных или статистическим способом.

Модели второго типа - это модели, выраженные с помощью систем уравнений относительно эндогенных

величин. Они выражают обычно балансовое соотношение между различными экономическими показателями и

используются для нахождения сбалансированных плановых решений (например, модель межотраслевого

баланса).

Третья группа - модели оптимизационного типа. Основную часть такой модели составляют системы

уравнений или неравенств относительно эндогенных величин. При этом необходимо найти такое решение этой

системы, которое давало бы оптимальное (т. е. максимальное или минимальное в зависимости от постановки

задачи) значение некоторого экономического показателя. Основными моделями этого типа, применяемыми в

планировании, являются задачи линейного программирования.

К четвертой группе относятся имитационные модели, которые используются в составе человеко-машинных

или игровых имитационных систем.

ю

Пятую группу составляют более сложные образования - такие, как системы и комплексы взаимосвязанных моделей, относящихся к перечисленным выше типам.

Развитие систем моделей позволяет точнее отразить самые различные аспекты планирования и функционирования экономических объектов, в частности, находить оптимальные решения, сочетающие рациональное соотношение между отраслевым и региональным аспектами планирования и управления.

Основные классы экономико-математических моделей

Экономико-математическая модель — совокупность математических выражений, описывающих

экономические объекты, процессы и явления, исследование которых позволяет получить необходимую

информацию для реализации целей управления моделируемой системой.

Экономико-математические модели можно подразделить на классы по ряду признаков: по цели моделирования;

по характеристике моделируемого объекта; по исследуемым экономическим процессам и содержательной

проблематике; по используемому инструментарию; по характеру описания случайных процессов; по способу

отражения фактора времени.

По целевому назначению экономико-математические модели делятся на:

• теоретические, используемые при исследовании общих свойств и закономерностей экономических процессов;
  

• прикладные, используемые для решения конкретных экономических задач (модели экономического анализа,
  прогнозирование, управление).
  

Экономико-математические модели могут предназначаться для исследования разных сторон народного хозяйства (производственно-технологической, территориальной) и его отдельных частей. При классификации моделей по исследуемым экономическим процессам и содержательной проблематике выделяются модели народного хозяйства в целом и его отдельных подсистем - отраслей, регионов и т. д., комплексы моделей производства, потребления, формирования и распределения доходов, трудовых ресурсов, ценообразования, финансовых связей

Различают дескриптивные и нормативные модели. Дескриптивные модели объясняют наблюдаемые факты или дают вероятностный прогноз. Примерами дескриптивных моделей являются производственные функции и функции потребительского спроса, построенные на основе обработки статистических данных. Нормативные отвечают на вопрос: как это должно быть - т. е. предполагают целенаправленную деятельность. Примером нормативных моделей являются модели оптимального планирования, формализующие тем или иным способом цели экономического развития, возможности и средства их достижения. По характеру отражения причинно-следственных связей различают модели жестко детерминистские и модели, учитывающие случайность и неопределенность. В результате накопления опыта использования жестко детерминистских моделей были созданы реальные возможности для успешного применения более совершенной методологии моделирования экономических процессов, учитывающих стохастику и неопределенность; проведения многовариантных расчетов и модельных экспериментов с вариацией конструкции модели и ее исходных данных; изучения устойчивости и надежности получаемых решений; выделения зоны неопределенности; включения в модель резервов; применения приемов, повышающих приспособляемость (адаптивность) экономических решений к вероятным и непредвиденным ситуациям. Получают распространение модели, непосредственно отражающие стохастику и неопределенность экономических процессов и использующие соответствующий математический аппарат: теорию вероятностей и математическую статистику, теорию игр и статистических решений, теорию массового обслуживания, теорию случайных процессов.

По способам отражения фактора времени экономико-математические модели делятся на статические и динамические. В статических моделях все зависимости относятся к одному моменту времени. Динамические модели характеризуют изменение экономических процессов во времени. В моделировании рыночной экономики особое место занимают равновесные модели. На их основе на микроэкономическом уровне моделируются оптимизационные модели. На макроуровне равновесные статические модели помогают исследовать состояние экономических систем. Экономическая динамика на макроуровне описывается с помощью моделей роста (модель магистрального типа, модель Харрода-Домара, модель Солоу и др.).

Экономико-математическая модель, как правило, включает три основные составные части:

1) целевую функцию, или функционал модели — математическое выражение цели;

2. систему срункциональных ограничений, определяющих пределы изменения исследуемых характеристик объектов,
   процессов или явлений;
   
3. систему параметров модели, фиксирующих условия проведения модельного эксперимента (система норм, нормативов,
   временные параметры реального времени, системного времени, начальные условия и т.п.).
   

В общем виде компонента экономико-математической модели системы в виде алгоритма связи параметров может быть записана в виде:

Y=Ffaai), где х/—управляемые (экзогенные) переменные; факторы; входы; а/ — неуправляемые переменные;

и

Y — зависимые (эндогенные) переменные, отклики, исходы;

F — определяет вид функциональной зависимости, играет роль оператора преобразования.

Управляемые переменные — набор мероприятий и их параметров, которыми может управлять лицо, принимающее решение (ЛПР). Так, приобретая автомобиль, покупатель может выбирать марку и модель автомобиля, дополнительное оборудование салона, способ финансирования покупки и т.д. Эти переменные могут быть количественными (например, мощность двигателя автомобиля) или качественными (например, цвет автомобиля). Набор (вектор) управляемых переменных характеризует выбор.

Выбор, то есть принятие решения — это процесс нахождения линий поведения (стратегий), определяемых значениями одной или большого числа управляемых переменных. Должно существовать не менее двух возможных стратегий, в противном случае проблемы не возникает, так как нет выбора. В принципе, возможны ситуации, в которых может существовать и бесконечное множество линий поведения. Неуправляемые переменные — ситуации, охватываемые проблемой, которыми не может управлять лицо, принимающее решение, но которые совместно с управляемыми переменными могут влиять на результат его выбора. Например, от покупателя не зависят налог на доход от продажи автомобиля и затраты на получение водительских прав, хотя они влияют на результат — стоимость покупки. Эти переменные также могут быть количественными или качественными. В совокупности они образуют окружающую среду (фон) проблемы. Следует иметь в виду, что неуправляемым переменным совсем не обязательно присуще свойство неуправляемости: просто они могут регулироваться другими лицами (организациями). Налог с оборота регулируется законодательными органами; поступление на промышленное предприятие заказов на изготовление продукции не зависит от руководителя производственного отдела, но оно может находиться под контролем маркетинговой службы; в иерархической организации каждый уровень управляет теми переменными, которые не могут контролироваться более низкими уровнями.

Возможные исходы (отклики) — это зависимые переменные, которые зависят как от выбора, так и от неуправляемых переменных. Например, покупатель может приобрести либо действительно хороший автомобиль, либо широко разрекламированную, но неудачную модель. Заметим, что должно быть не менее двух возможных исходов, в противном случае выбор не влияет на исход. Более того, как минимум, два возможных исхода должны быть неравноценными, так как в противном случае не имеет значения, какое решение принято. Следует иметь в виду, что управляемые и неуправляемые переменные подвержены отклонениям, случайным (стохастическим) возмущениям, что, естественно, влияет на возможные исходы и должно учитываться при конструировании алгоритма.

При моделировании сложной системы исследователь обычно использует совокупность (агрегат) алгоритмов. Любая система может быть представлена различными способами, отличающимися по сложности и в деталях.

Методика моделирования.

Основой успешной методики моделирования является многоэтапный процесс отработки модели. Обычно начинают с более простой модели, постепенно совершенствуя ее, добиваясь, чтобы она отражала моделируемую систему более точно. До тех пор, пока модель поддается математическому описанию, исследователь может получать все новые ее модификации, детализируя и конкретизируя исходные предпосылки. Когда же модель становится неуправляемой (слишком сложной), проектировщик прибегает к ее упрощению и использует более общие абстракции.

Процесс моделирования, таким образом, носит итерационный характер и осуществляется в соответствии со следующими этапами.

1. Анализ проблемы и определение общей задачи исследования.
   
2. Декомпозиция общей задачи на ряд более простых подзадач, образующих взаимосвязанный комплекс.
   
3. Определение четко сформулированных целей и их упорядочение.
   
4. Поиск аналогий или принятие решений о способе построения подмоделей.
   
5. Выбор системы управляемых и неуправляемых переменных, необходимых параметров.
   
6. Запись математических соотношений между ними.
   
7. Анализ полученной модели и начало итерационного конструирования: расширение или упрощение модели.
   

Упростить модель можно, выполнив одну из перечисленных ниже операций:

• превращение переменных величин в константы;
  
• превращение вероятностных факторов в детерминированные;
  
• исключение некоторых переменных или их объединение;
  
• использование предположений о линейном характере зависимостей между переменными;
  
• введение жестких исходных предпосылок и ограничений;
  
• уменьшение количества степеней свободы путем наложения более жестких граничных условий.
  

Расширение модели предполагает действия, обратные перечисленным.

Процесс создания модели завершается ее проверкой (обоснованием). Обоснование модели предполагает

выполнение следующих процедур:

Верификация, проведение которой убеждает в том, что модель ведет себя так, как было задумано.

12

Оценка адекватности — проверка соответствия между поведением модели и поведением реальной системы. Проблемный анализ — формулировка значимых выводов на основе результатов, полученных в ходе моделирования.

Как показывает опыт, наибольшая обоснованность модели достигается:

• использованием здравого смысла и логики;
  
• максимальным использованием эмпирических данных;
  
• проверкой правильности исходных предположений и корректности преобразований от входа к выходу;
  
• применением на стадии доводки модели контрольных испытаний модели, подтверждающих работоспособность модели;
  
• сравнением соответствия входов и выходов модели и реальной системы (если они доступны) с использованием
  статистических методов и тестовых испытаний;
  
• проведением, когда это целесообразно, натурных или полевых испытаний модели или ее подмоделей;
  
• проведением анализа чувствительности модели по отношению к изменяющимся внешним условиям;
  
• сравнением результатов модельных прогнозов с результат функционирования реальной системы, которая подвергалась
  моделированию.
  

Необходимые термины и понятия из теории управления

Для увеличения шансов на благоприятный исход необходимо активное воздействие на ход событий и структуру наших

отношений с ними, иными словами, необходимо управление, т.е. целенаправленное воздействие одной системы (субъекта

упр-я.) на другую (объекта упр.-я) , выбранное из мн-ва возможных воздействий на основе имеющейся для этого

информации с целью изменения ее поведения (состояния) в соответствии с изменяющимися условиями внешней среды и

улучшения функционирования или развития объекта упр-я.

Кибернетика как наука об управлении изучает не все системы вообще, а только управляемые системы.

Одной из характерных особенностей управляемой системы является способность изменять свое движение, параметры,

переходить в различные состояния под влиянием различных управляющих воздействий.

Всегда существует некоторое множество состояний системы, из которого производится выбор предпочтительного

состояния, если речь идет об управляемой системе. Где нет выбора, там нет и не может быть управления.

Важные термины и понятия:

система управления; объект управления; управляющие воздействия; возмущающие воздействия; сигналы управления; управляющее устройство (субъект упр.-я, упр. система, исполнительные органы (исполнительная система)); закон (алгоритм) управления; принцип «обратной связи», принцип Беллмана; оптимальное управление; критерии эффективности; основные типы задач управления: стабилизация, выполнение программы, слежение и оптимизация; условия существования системы управления: организованность, разнообразие (закон необходимого разнообразия), динамичность, наличие прямых и обратных связей, наличие цели управления, управляемость; виды связей в СУ: прямая, обратная (внешняя, внутренняя, положительная, отрицательная, жесткая, гибкая), понятие коэффициента обратной связи.

Иерархические системы управления. Важный класс систем управления образуют системы произвольной природы (технические, экономические, биологические, социальные) и назначения, имеющие многоуровневую структуру в функциональном, организационном или каком-либо ином плане, Характерными признаками иерархических систем управления (ИСУ) являются: вертикальная декомпозиция системы на подсистемы, приоритет подсистем верхнего уровня по отношению к нижележащим, наличие обратных связей между уровнями. Следует иметь в виду, что при декомпозиции на любых уровнях иерархии можно выделить описанную ранее триаду: управляющую систему (субъект управления), управляемую систему (объект управления) и исполнительную систему (исполнительные органы). Широкое использование и универсальность ИСУ обусловлены рядом преимуществ по сравнению с системами радиального (централизованного) управления:

• свобода локальных действий в рамках наложенных ограничений;
  
• возможности целесообразного сочетания локальных критериев функционирования отдельных подсистем и глобального
  критерия оптимальности системы в целом;
  
• возможности сжатого, агрегированного представления актуальной информации о результатах управления, поступающей
  по каналам обратной связи;
  
• повышенная надежность системы управления, наличие свойств управляемости, адаптивности, организованности и ряда
  других свойств, специфичных для конкретных систем;
  
• универсальность концепции управления и подходов к решению задач управления в ИСУ;
  
• экономическая целесообразность по сравнению с системами управления иной структуры. Последнее качество требует
  обоснования в каждом конкретном случае.
  

Теория управления ИСУ включает следующие основные разделы:

• структурный анализ и синтез ИСУ;
  
• проблема координации в ИСУ;
  
• оптимизация функционирования ИСУ.
  

Принцип иерархичности управления является выражением целостности систем; он, предопределяя организованность, позволяет найти способы управления сложными системами. Если организованность системы отсутствует, невозможно определить задачи управления даже для простых объектов.

Этот принцип предусматривает способ расчленения системы на элементы и взаимодействующие подсистемы и многоступенчатого построения управляющих систем, в которых функции управления распределяются между со­подчиненными частями. В расчлененной системе одна часть оказывается «вложенной» в другую и является ее структурной составляющей. В такой системе существует взаимосвязь подсистем по одним отношениям и их свойствам и независимость по другим.

13

Лекция 4

Анализ системы общественного потребления

Важной подсистемой экономики является подсистема общественного потребления. Эта подсистема

определяет требования к системе общественного производства. С другой стороны, общественное

потребление выступает своеобразным индикатором эффективности экономики в целом.

Важными понятиями, характеризующими состояние системы общественного производства, являются: спрос,

предложение, рынок.

Спрос — совокупность требований на товар, который потребители купят по той или иной цене в данный

период при прочих равных условиях. Отражая предпочтения покупателей на рынке, спрос может быть

индивидуальным и рыночным. Шкала спроса — это таблица, показывающая количество товаров, которое

было бы куплено по данной цене в данный период времени.

Таблица 1. Шкала спроса одного покупателя на мясо за месяц

Цена (у.е./кг)	Величина спроса (кг)
8	8,3
10	7,2
12	6,1
14	5.5
16	4,9

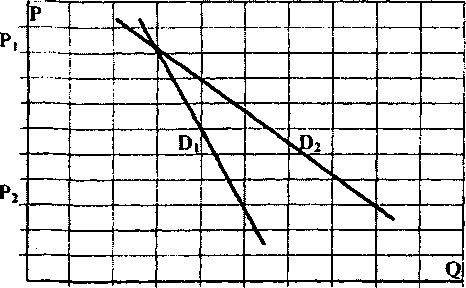
Рис. 1. Влияние рыночных механизмов на кривую спроса

							->	D2
					>		л	-s.	•~s
			— „_	\	4		*<
					->*	--х		**.
						D3	>

Когда цена на один из взаимозаменяемых товаров растет, спрос на другой товар повышается и кривая спроса сдвигается вправо. Увеличение цен на мясо вызывает рост спроса на колбасные изделия, а рост цен на кофе определяет возрастание спроса на чай. Спрос на один товар прямо пропорционален цене другого товара. Спрос на один из взаимодополняющих товаров обратно пропорционален цене другого товара. Так, с ростом цен на автомобили падает спрос на бензин, и кривая спроса сдвигается влево. С изменением вкусов или предпочтений изменяется спрос. Появление новых товаров — субститутов — вызывает падение спроса на искомый товар. Появление новой информации о товарах, переход населения в другую референтную группу, реклама и мероприятия по стимулированию сбыта, другие факторы вызывают изменение спроса.

Ожидания людей в отношении будущих цен на товары, будущих доходов и будущих возможностей приобрес­ти товары могут изменить спрос на товар, так как люди будут стремиться предохранять себя от возможных будущих потерь. Например, предположение об ожидаемом повышении цен на автомобили в будущем году может способствовать увеличению текущего спроса на машины (кривая спроса сдвигается вправо), в то время как ожидаемое повышение цен на бензин может привести к снижению спроса на автомобили. Важным аналитическим показателем чувствительности спроса к изменению влияющих на него факторов яв­ляется показатель эластичности.

Таблица 2. Изменение выручки

Изменение цены	Изменение общей выручки
	Эластичный спрос	Неэластичный спрос	Единичная эластичность спроса
рост	снижение	рост	без изменений
снижение	рост	снижение	без изменений

Таблица 3 Шкала предложения количества мяса, предлагаемого производителем в течение месяца

Цена (у.е. /кг)	Величина предложения (кг)
8	200
10	300
12	400
14	500
16	650
18	800