Государственный университет высшая школа экономики л. Л. Любимов введение в экономическую теорию в 2-х книгах

Вид материала

Книга

Содержание § 108. агрегированный товарный рынок, налоги и государственные расходы Y, которое удовлет­воряет спросу на товарных рынках, мы находим равновесный Y

Подобный материал:

• Правительство Российской Федерации Государственный университет Высшая школа экономики, 110.67kb.
• Методика использования показателей демократии при моделировании имущественного неравенства, 147.7kb.
• Джон Р. Хикс. "Стоимость и капитал", 4314.44kb.
• Программа обучения, 37.35kb.
• Правительство Российской Федерации Государственный университет Высшая школа экономики, 230.77kb.
• В. П. Бусыгин Государственный университет-Высшая школа экономики; г. Москва, 302.53kb.
• Правительство Российской Федерации Государственный университет Высшая школа экономики, 182.83kb.
• Правительство Российской Федерации Государственное образовательное бюджетное учреждение, 69.06kb.
• М. А. Розов 61 Релятивизм: абстрактная теория или методологическая практика?, 4106.79kb.
• Правительство Российской Федерации Государственный университет Высшая школа экономики, 323.63kb.

§ 108. АГРЕГИРОВАННЫЙ ТОВАРНЫЙ РЫНОК, НАЛОГИ И ГОСУДАРСТВЕННЫЕ РАСХОДЫ

Включение государственных закупок (G) в совокупный спрос изменяет условия равновесия на товарных рынках. Если в двухсекторной модели условие равновесия определя­лось как Y = С + I, то теперь оно выглядит как

Y = С + I + G.

Государственные закупки добавляются к AD, но они одновременно снижают частные потребительские расходы через налоговые изъятия. Поскольку располагаемый доход является частью У, которую потребители расходуют или сберегают, потребительская функция должна быть изменена так, чтобы потребление зависело от располагаемого дохода:

С = C₀ + C₁ Y_D или С = C₀ + C₁(Y - T).

Мы предполагаем, что включение G не изменяет инве­стиционного спроса и его связи с Y и ставкой процента, так что инвестиционная функция остается той же. Мы лишь перепишем ее в следующем виде:

1= I₀ + I₁ Y – I₂R.

Теперь в уравнении с основным условием равновесия (Y = С + I + G) мы заменим члены С и Y на приведенные выражения для потребительского и инвестиционного спроса, а также добавим автономный уровень государственных расхо­дов (G) к совокупному спросу и получим новое условие равновесия. Но замещения, ведущие к этому условию равно­весия, мы покажем через последовательные шаги:

Y = C₀ + C₁ Y_D + I₀ + I₁ Y - I₂R + G.

Затем, поскольку располагаемый доход равен (Y — Т),

Y = C₀ + C₁(Y – T) + I₀ + I₁ Y - I₂R + G.

Теперь заменяем Т на налоговую функцию, так что результатом этих замещений является условие равновесия на товарных рынках:

Y = C₀ + C₁ [Y - (T₀ + T₁ Y)] + I₀ + I₁ Y - I₂R + G. (20.1)

Это последнее уравнение может быть перестроено так, бы получился график комбинаций Y и ставки процента (R), для которых соблюдается условие равновесия на товарных рынках:

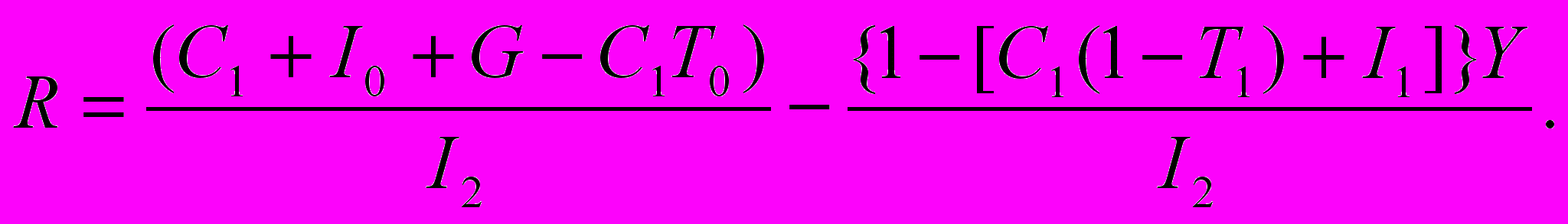(20.2)

Это сложное выражение, которое нелегко интерпретировать и не нужно запоминать. Мы можем применить его к гипотетическим величинам С, I, T, G:

С = 80 + 0,7Y_D; I = 250 + 0,1Y - 10R; Т = 300 + 0,2Y.

Допустим, что G = 1290; тогда условие равновесия на товарных рынках будет:

Y = С + I + G =

= 80 + 0,7Y_D + 250 + 0,1Y - 10R + 1290 =

= 80 + 0,7 [Y- (300 + 0,2Y)] + 250 + 0,1Y- 10R + 1290.

Приведение подобных дает:

Y = (80 - 210 + 250 + 1290) + (0,56Y + 0,1Y) - 10R.

Переводя член уравнения со ставкой процента R в левую сторону уравнения, а член уравнения с Y в правую сторону и разделив обе части уравнения на 10, получаем:

R = 141 - 0,034Y.

Если R = 5%, то

0.034Y = 141 - 5 = 136,

Y = 4000.

Таким образом, при приведенных допущениях равновес­ный уровень Y = 4000.

При заданной ставке процента, как мы видим, равновес­ный Y может быть определен из условия равновесия: если R известна, то известен и уровень Y, соответствующий этой точке.

Решая уравнение (20.1) для значения Y, которое удовлет­воряет спросу на товарных рынках, мы находим равновесный Y. Решение включает перевод членов уравнения, относящихся к Y₁, в левую сторону и разложение на множители:

Y[1- C₁(1 – T₁) – I₁] = C₀ + I₀ – I₂R + G – C₁T₀.

Деление обеих сторон на [1 — C₁(1 - T₁) — I₁] дает нам следующее выражение равновесного дохода при данной став­ке процента (R):

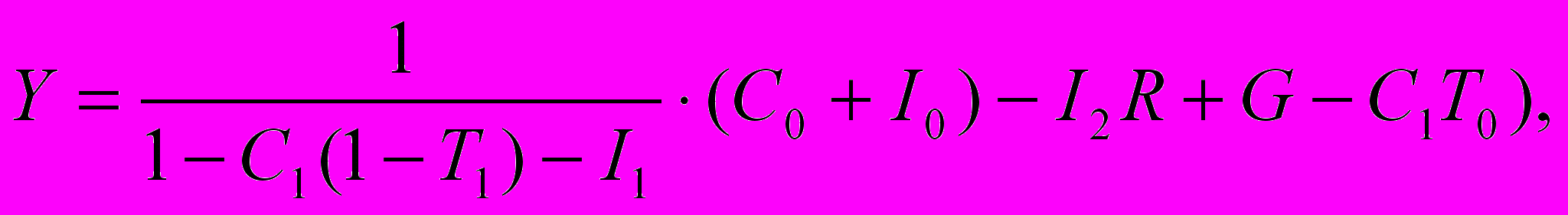
равновесный Y =

мультипликатор автономных расходов



автономные расходы

Переписывая мультипликатор автономных расходов, в котором применяются предельные склонности, получаем:

мультипликатор автономных расходов

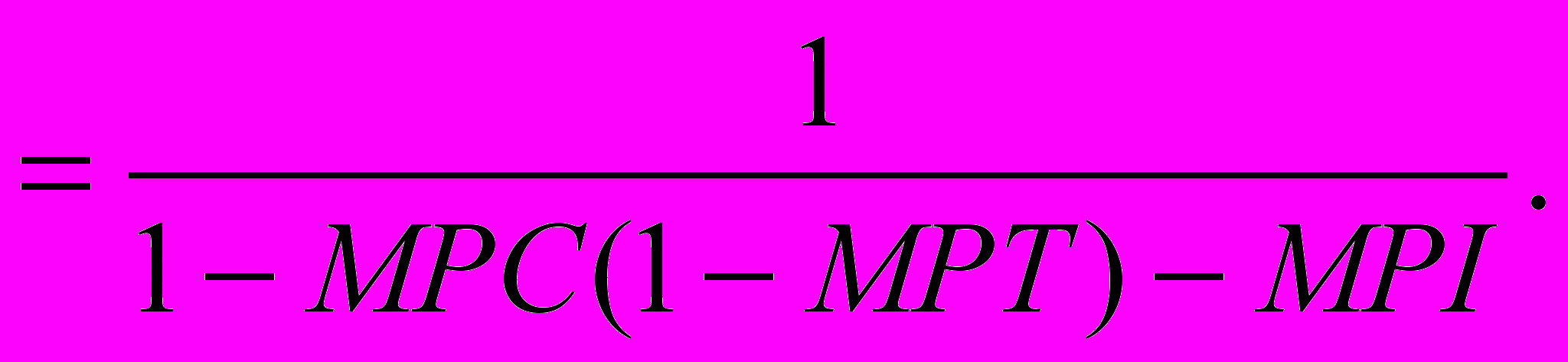(20.3)

В этом выражении G и (G — C₁T₀), т.е. госрасходы на товары и услуги и автономная часть налогов, являются новыми членами по сравнению с выражением, которое можно было бы применить для двухсекторной модели, где есть только С и I. В целом величина G всегда существенно больше, чем чисто автономная часть налоговых поступлений. Налоги реагируют на изменения Y, так что предельная склонность к налоговому изъятию (МРТ) неизбежно должна была появиться в формуле мультипликатора автономных расходов. Этот мультипликатор зависит от МРТ (или T₁) так же, как и от предельной склонности к потреблению (МРС, или C₁) и предельной склонности к инвестициям (I₁ или MPI). Более высокие налоги сокращают располагаемый доход (Y_D), который остается после любого повышения налогов. Это воздействие отражается на мультипликаторе (20.3), так как МРТ увеличивает знаменатель и уменьшает величину мульти­пликатора. Введенный нами государственный сектор в форме G увеличивает совокупный спрос (AD) через госзакупки товаров и услуг и понижает совокупный спрос через чистые Залоговые поступления (T).

Мультипликатор автономных расходов показывает нам, как изменится AD, когда изменяется автономная часть по­требительских, инвестиционных и госрасходов. Но мульти­плицируемое воздействие изменений в автономных расходах при наличии налогов отличается от такого же воздействия при отсутствии налогов. Поскольку налоги являются функци­ей уровня дохода (Y), постольку они создают налоговые утечки (повышающиеся чистые налоговые поступления, свя­занные с увеличением Y; так как налоговые утечки сокраща­ют вызванный увеличением Y рост расходов, они уменьшают величину мультипликатора), снижающие мультипликатор. Чем сильнее налоговая утечка, тем меньшим будет конечное воздействие первоначального изменения в расходах. Следую­щее уравнение демонстрирует воздействие изменения в авто­номных расходах на Y:

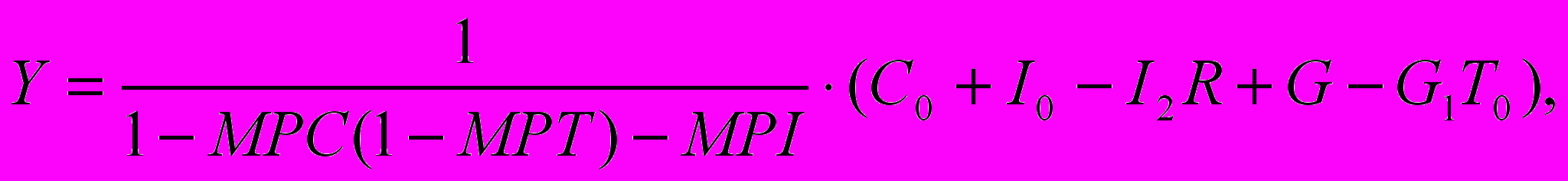(20.4)

изменение Y =

мультипликатор автономных расходов



изменение в автономных расходах

Поскольку повышение предельной склонности к налого­вому изъятию (ставка налога, Е₁) снижает величину мульти­пликатора, то чем выше налоговая ставка, тем ниже воздей­ствие мультипликатора на равновесный Y.