Geum.ru

Государственный университет высшая школа экономики л. Л. Любимов введение в экономическую теорию в 2-х книгах

Вид материалаКнига

Содержание


Тема 19.совокупные расходы и мультипликатор
§ 102. баланс совокупных расколов
SRAS Кейнс считал уместным лишь горизонтальный сегмент этой кривой (см. рис. 18-1 в предыдущей теме, отрезок АВ).
Y, какое мы имеем в точке А
Подобный материал:
1   ...   12   13   14   15   16   17   18   19   ...   60

ТЕМА 19.
СОВОКУПНЫЕ РАСХОДЫ И МУЛЬТИПЛИКАТОР


Цель изучения темы состоит в том, чтобы узнать:
  • как автономный рост совокупных расходов воздейству­ет на мультиплицированное увеличение реального ВНП;
  • как определить величину мультипликатора расходов;
  • как определить величину мультипликатора для раз­личных видов государственной деятельности;
  • как определить мультипликатор для внешней тор­говли;
  • что такое парадокс бережливости.

В предыдущей теме мы уже узнали, что рост автоном­ных потребительских расходов вызывает кратно увеличенный рост совокупного дохода. Этот феномен, обнаруженный Кейнсом, получил название расходного мультипликатора или мультипликатора расходов — пропорции изменения реального ВНП в ответ на изменение в автономных расходах. Мы рассмотрели потребление (совокупные потребительские рас­ходы) как компонент совокупных расходов и часть простей­шей теории определения совокупного дохода, или ВНП. Сей­час можно показать, как эта теория действует. В тождестве Y = С + I + G, помимо потребления (С), есть еще инвестиции (I) и государственные расходы на покупку товаров и (G). Значения I и G нужно получить вне модели, в то время как С и Y устанавливаются внутри модели. Переменные определяемые за пределами модели, называются экзогенными переменными, а определяемые внутри — эндогенными переменными. В макроэкономическом анализе идея о том, эндогенные переменные должны одновременно удовлетворять какому-то числу взаимосвязей (отношений), является важнейшей. Простейшая модель состоит из двух основных отношений: 1) тождества совокупного дохода (YD = С + I + G); 2) потребительской функции*. Потребительская функция фактически говорит нам о том, что С положительно зависит YD (обе константы — а и b — имеют положительный знак). Очень важно различать константы и переменные. Часто константы называют коэффициентами (а и b — коэффициенты), а С и YD в потребительской функции являются переменными. Переменные изменяются, а константы имеют фиксирован­ные значения.

Потребительская функция может быть выражена в кате­гориях Y, а не YD. Располагаемый доход (YD) равен Y (сово­купный доход) минус налоги. Если совокупный налог как норма (ставка) является константой (t), то величина сово­купного налога равна tY. Тогда YD = YD - tY = (1 - t)Y. Заменяя YD на (1 - t)Y, мы можем переписать потребительскую функцию как С = а + b (1 — t)Y.

Итак, для определения значений двух эндогенных пере­менных макромодели — С и Y — могут быть использованы два основных отношения (тождество дохода и потребитель­ская функция). Значения C и Y обусловлены требованием того, чтобы оба отношения удовлетворяли им одновременно.

§ 102. БАЛАНС СОВОКУПНЫХ РАСКОЛОВ


Еще раз вернемся к простейшему графику кейнсианской макромодели. На рис. 19-1 совокупные расходы — на оси Y, а реальный ВНП — на оси X. Кривая АЕ и биссектриса уг­ла 0 пересекаются в точке равновесия, где C и Y удовлетво­ряют одновременно и потребительской функции, и доходно­му тождеству. Кривая АЕ показывает зависимость совокупных расходов от Y. Совокупные расходы являются суммой потре­бительских, инвестиционных и государственных расходов. В этой модели от Y зависят только потребительские расходы (через потребительскую функцию). I и G являются экзоген­ными переменными. Таким образом,

АЕ = а + b(1 – t)Y + I + G, где АЕ включает потребительскую функцию. В любой точ­ке биссектрисы Y = АЕ. Следовательно, кривая АЕ представ­ляет тождество совокупного дохода. Эту кривую иногда на­зывают «биссектрисой Кейнса», а сам график — «крестом Кейнса».

Еще раз вспомним, что на кривой SRAS Кейнс считал уместным лишь горизонтальный сегмент этой кривой (см. рис. 18-1 в предыдущей теме, отрезок АВ). Краткосрочные колебания фактического Y происходят внутри этого сегмента. В то же время любой сдвиг кривой AD вызывает равное по величине изменение Y. Поэтому Кейнс отказался от кривой SRAS и заменил ее на биссектрису угла 0. Вместе с тем он утверждал, что в краткосрочном плане цены являются негиб­кими («липкими»), вследствие чего отказался в своей макро­модели и от такой переменной, как Р. Таким образом, он построил модель доходы—расходы, отвергнув базовую макро­модель AD/SRAS. Обе модели важны для макроэкономическо­го анализа. Рассмотрение совокупных расходов позволяет от­дельно анализировать детерминанты совокупного спроса как переменные (С, I, G), но за счет допущения того, что Р является константой. В свою очередь, рассмотрение AD позво­ляет определять Р за счет того, что роль С, I, G не рассматривается.



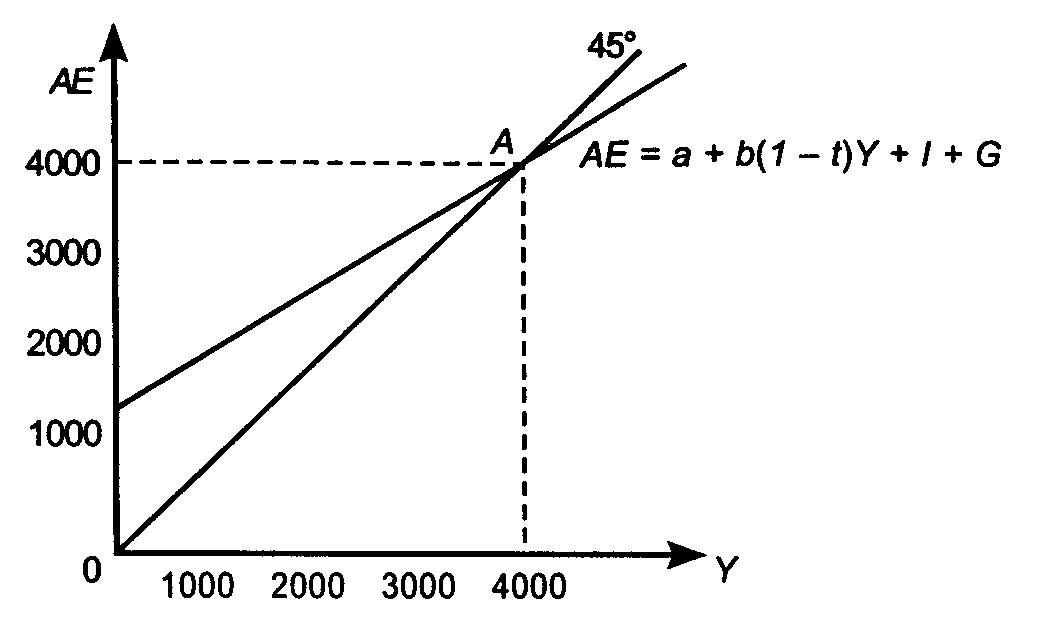
Рис. 19-1

Точка пересечения кривой АЕ и биссектрисы угла 0 является точкой А, где С и Y удовлетворяют обоим отноше­ниям модели. На биссектрисе удовлетворяется тождество дохода, а на кривой АЕ — потребительская функция. Точка пересечения дает искомое значение Y. В этой точке совокуп­ные расходы равны совокупным доходам, а потребительские расходы удовлетворяют потребительской функции. Биссект­риса круче, чем кривая АЕ. Наклон биссектрисы равен 1. Наклон потребительской функции равен b(1 - I), т. е. меньше 1. Так как у обеих линий наклоны разные, они должны всегда пересекаться.

Уровни С и Y можно также определить алгебраически:

Y = а +b(1 - I) Y + I + G.

а + b(1 - t)Y является потребительской функцией, которая заменила С в тождестве дохода. Данное уравнение содержит одну эндогенную переменную — Y, в то время как I и G являются экзогенными переменными. Переменная Y имеется в обеих сторонах уравнения. Чтобы решить его для Y, нужно перенести оба члена, содержащие Y, в левую часть уравне­ния. Поступая так, мы увидим, что значение Y, при котором решается это уравнение, задано:



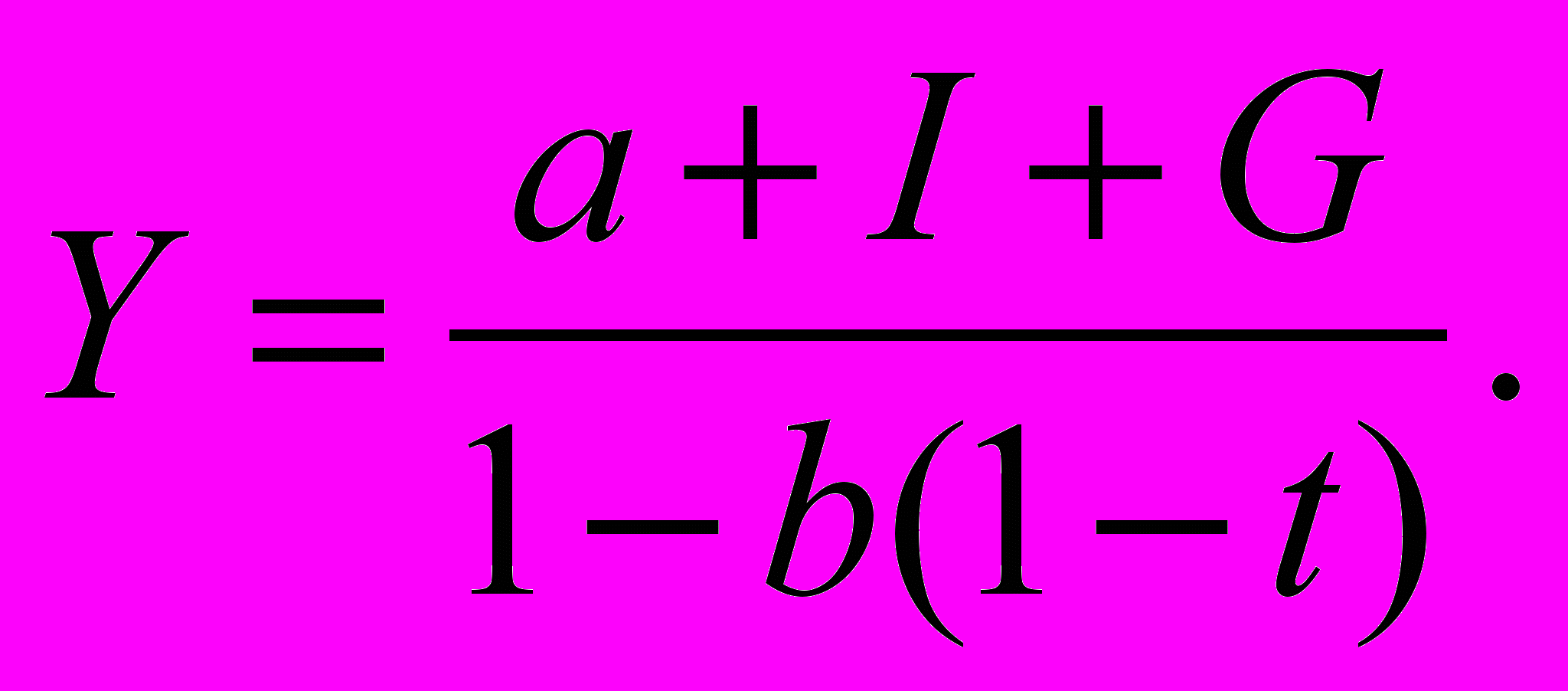
Это и есть решение модели, которое точно соответствует тому значению Y, какое мы имеем в точке А на рис. 19-1. В этом случае значение С может быть получено включением значения Y в потребительскую функцию, т. е. С = а + b (1 — I) Y, где значение Y взято из предыдущего уравнения.

Теперь мы можем подытожить наше краткое рассмотре­ние вопросов, связанных с балансом расходов. Во-первых, простая модель определения Y включает два отноше­ния: потребительскую функцию и тождество дохода. Модель определяет две эндогенные переменные — потребление и совокупный доход. Две экзогенные переменные (I и G) устанавливаются вне модели. Во-вторых, баланс совокупных расходов достигается, когда потребители выбирают уровни С на основе уровня совокупных доходов, который является таким же, как и уровень Y = С + I + G. И, в-третьих, баланс расходов достигается при таких уровнях С и Y, которые удовлетворяют и потребительской функции, и тождеству дохода.

Важно постигнуть логику поиска величин С и Y, которые удовлетворяют потребительской функции и тождеству дохода. Когда люди больше расходуют на покупки, фирмы больше производят. Для этого они нанимают больше работников, общая сумма доходов растет, растут и потребительские рас­ходы. Когда достигается баланс расходов и доходов, доход, получаемый потребителями, равен доходу, который образу­ется их расходами (т. е. доходу производителей). Но допустим, что потребители расходуют слишком много по сравнению со своими доходами. В этом случае экономика начинает терять устойчивость, люди сокращают потребление и фирмы теперь производят меньше. Доходы работников сокращаются, пока вновь не будет достигнут баланс.

Но откуда мы знаем, что снижение доходов и расхо­дов будет идти именно до достижения точки равновесия, а не продолжаться вплоть до кризисного потрясения эконо­мики? Когда С снижается вследствие уменьшения доходов, С снижается меньше, чем доходы. Предельная склон-ость к потреблению ниже 1, так что снижение Y ведет относительно меньшему снижению С. Поэтому меньшее снижению С генерирует меньшее снижение Y во втором круге движения циркуляционных потоков. Этот процесс обоюдного снижения ведет к более низкой точке общего баланса.