Geum.ru

Корзинкин Владимир Анатольевич Москва 2009 литература

Вид материалаЛитература

Содержание


Результат 2 Одни из известных истинных неаристотелевских силлогизмов ЕЯ содержится в обобщенном. Он близок к Аристотелевскому “А
Рассмотрим такой
Рассмотрим следующий силлогизм
Подобный материал:
1   2   3   4   5   6   7   8

a







b










c




Результат 1:

Один из истинных силлогизмов Аристотеля содержится в обобщенном силлогизме.


Cиллогизм 2 может быть записан так:

при 1 = 2


ab bc ac

,1 ,1 V,1

  


в контексте

 = ( ,1; ,1; ,1 )


Диаграмма Венна для этого случая такова:





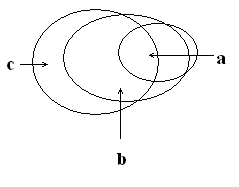
0 1/N  υ  1



Например, имеем:

 = 0.9

,1  1/N, 1]

Тогда можно вычислить υ:

(υ <= max (0;0;1-0.29)) – общая формула

υ – нижняя граница 3-ей детерминации

Составим следующую лингвистическую форму всего этого «Из того, что “почти все a - суть b” и “почти все b – суть c” следует, “что многие a – суть c”».

Лингвистическая форма контекста: “a, b, c встречается нередко” – это неаристотелевский истинный силлогизм известный в ЕЯ, и называется “силлогизмом бабушки”.

Результат 2

Одни из известных истинных неаристотелевских силлогизмов ЕЯ содержится в обобщенном. Он близок к Аристотелевскому “ААА”.


Есть ли в детерминационном (обобщенном) силлогизме истинные, но неизвестные силлогизмы?


§5. Силлогистика нередких свойств

Может ли РА так анализировать предпосылки, чтобы приходить к правильным рассуждениям так, как это не может делать человек?

Познакомимся с результатами исследования параметрического семейства силлогизмов:

 = {v( A );   (0,1); V (0,1}

 - параметр базиса квантификаторов

V – параметр контекста

A - базис квантификаторов L1 L2 L 3 L4

Аристотелев базис:

A0 = {1} (0,1 [0,1) {0} 

L1 L2 L 3 L4


a >  = 1/N; b >  ; c >  ;


Рассмотрим такой:




A = [1-,1], [,1], [0,1-], [0, ], 

L1 L2 L 3 L4


И возьмем параметр  < = 0,5, тогда получим A таким:




A = [0.9,1], [0,1], [0,0.9], [0, 0.1], 

L1 L2 L 3 L4



0  1- 1



0 – означает “никогда”

1 – означает “всегда”


Квантификаторы 
Аристотелевский предел 0<<=1/

Численные
Словесные
Численные

Словесные

L1 = [ 1-; 1 ]
часто
L1 = {1}
Всегда, либо

(все…есть суть…)

L2 = [ ; 1 ]
нередко
L2 = (; 1]
Бывает, или

(некоторые…суть…)

L3 = [ 0; 1- ]
нечасто
L3 = [ 0; 1-)
Не всегда, или

(некоторые …не суть…)

L4= [ 0;  ]
редко
L4= {0}
Никогда, или

(ни один…не суть…)


= ([, 1], [, 1], [, 1], [0,1]), где есть ограничения  снизу, следовательно рассматриваются редкие свойства.


Рассмотрим следующий силлогизм:

a  b , b  c a  c

[0, ] [0, ] [0, ]

  


 - параметр контекста,  - полнота

Если взять произвольную точку в квадрате  x , то возможны следующие случаи:

1). Существование или несуществование силлогизма

2). Если силлогизм существует, то он может быть истинным или ложным

3). Если силлогизм истинный, то есть разные виды:
  • тавтология, т.е. всегда верные
  • тривиальные, но не тавтологии, т.е. зависят от параметра
  • нетривиальные








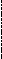
Можно показать, что в прямоугольнике  x , где  - параметр контекста,  - полнота, есть область, где нетривиальный силлогизм существует (в области G3 и G4), одни границы - открыты, другие - закрыты.

Пример лингвистической формы всего этого (контекста и силлогизма):

“Нередки свойства: любить читать книги, быть женщиной, иметь склонность к правонарушениям, поэтому если среди любителей чтения редко встречаются женщины, а среди женщин редко встречаются склонные к правонарушениям, то среди любителей чтения, склонные к правонарушениям встречаются “нередко”.

Можно проверить, что в Аристотелевском пределе, т.е. в таком (0   ,

0     ), этот силлогизм ложный.