Корзинкин Владимир Анатольевич Москва 2009 литература
| Вид материала | Литература |
- Веткин Владимир Анатольевич, кандидат физико-математических наук, доцент Винтайкина, 3941.49kb.
- Тэк сегодня среда, 25 февраля 2009 г. Часть 2 содержание, 828.56kb.
- Владимир Анатольевич Беляев (Помощник председателя), Муромский историко-художественный, 44.04kb.
- Маталасов владимир анатольевич, 1108.96kb.
- Хохлова Галина Ивановна. "Возможности разработки идеологии научного сообщества"., 12.17kb.
- Зеленский Владимир Анатольевич, начальник отдела консолидированной отчет, 598.05kb.
- Название дисциплины, 587.61kb.
- Фисинин Владимир Иванович Доктора наук Габитов Ильдар Исмагилович Зыкин Владимир Александрович, 2780.59kb.
- Маяковский Владимир Владимирович. Маяковский Владимир Владимирович (1893, с. Багдади, 59.82kb.
- Князья Владимир Святославич, Ярослав Мудрый, Владимир Мономах. 11. Культура Древней, 24.41kb.
Таблица, строки которой представляют собой объекты исследования, столбцы - признаки объекта или переменные, а на пересечении находятся свойства объектов или значения соответствующих переменных для объектов, называется матрицей данных (МД).
Свойства МД:
1). МД представляет собой универсальное средство описания в фиксированный момент времени однородных объектов исследования из всех областей знания (естественно - научных, технических, гуманитарных) и может содержать количественные и качественные значения переменных. К гуманитарным областям знаний, рассматриваемых в один период времени и отраженных в МД, относится экономика, маркетинг, социология, менеджмент, теория ЕЯ, но не относится история, исследование процессов, структура восприятия подвижной картины.
Примеры применения:
МД: из естественно - научной области
| Объекты | Признаки | ||
| X1 размер, см | Х2 путь, м | ХЗ время падения, с | |
| шар el | 2 | 1,5 | 0,55 |
| шар e2 | 1 | 1,5 | 0,55 |
| … | | | |
МД из области экономики (торговли)
| Марки телевизоров | Размер по диагонали | Четкость (число строк) | Страна производитель | Вес,кг | Цена,тыс.руб. |
| Sumsung | 70 | 1000 | Китай | 7 | 12 |
| | | | | | |
2). Измерения
Можно ли добиться одинаковой точности количественных и качественных значений МД?
Измерениями в любой области знания для данного периода времени называется процедура получения эмпирических (опытных) данных для заполнения МД. Измерения в естественнонаучных и технических областях чаще всего приводят к непрерывным числовым значениям (т.е. числам), а в гуманитарных областях к дискретным качественным значениям (т.е. словам). Связь между числовыми непрерывными значениями может быть представлена функцией, а экспериментальный разброс значений - некоторой функцией плотности вероятности (ФПВ). Например:
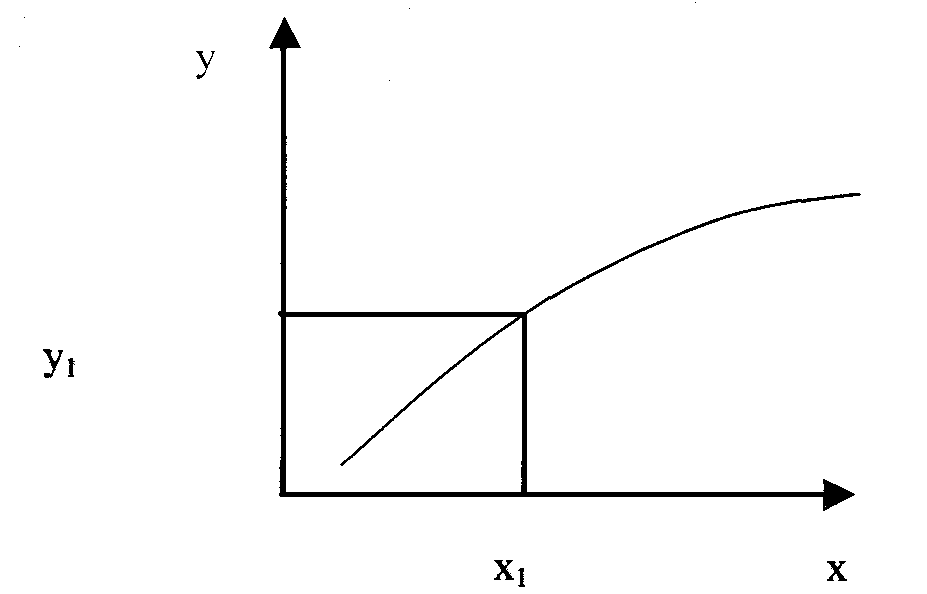
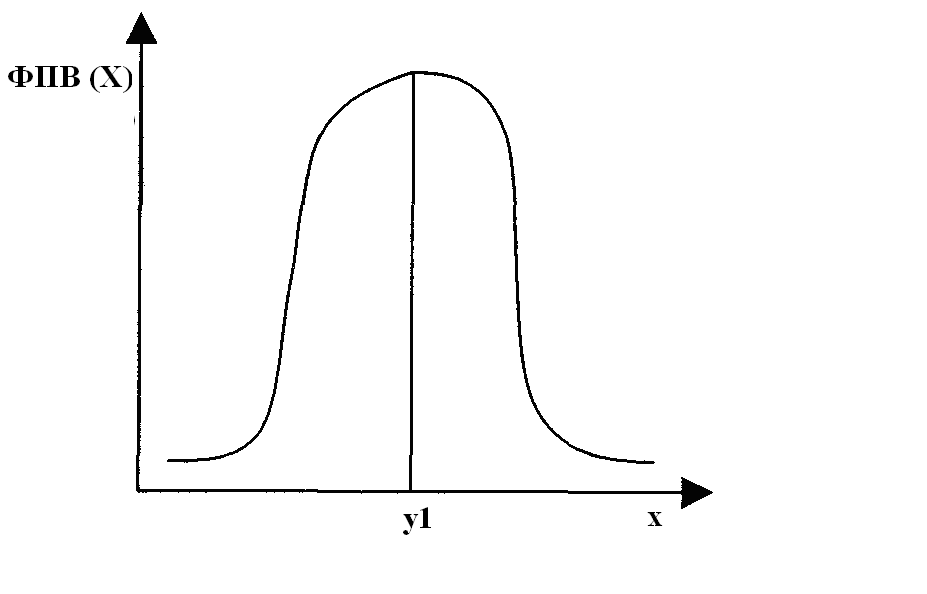
Дискретные качественные значения в простом случае представлены такими МД и таблицей сопряженности:
В простейшем случае
МД:
| Объекты | Признаки | |
| X | Y | |
| 1 | а | 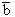 |
| 2 | а | b |
| 3 | 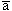 | b |
| … | | |
Таблица сопряженности:
| y | | | |
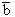 | 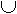 | 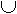 | |
| b | 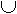 | 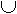 | |
| | a | 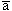 | x |
- - это числа объектов, которые обладают совокупностью соответствующих свойств.
В технике и естественных науках обеспечение точности измерений изучается в соответствующих курсах - схожими способами измерения (длина, время и т.д.). В гуманитарных областях точность измерений обеспечивается своими методами (например, в социологии применяется так называемая техника проведения социологических опросов).
Особенностью гуманитарных измерений является то, что прибор (человек, проводящий измерения) оказывает влияние на результаты измерения, так как измерение - есть акт общения людей. На точность влияет, например, этика, степень доверия и т.д. Для нас главное, что техника обеспечения точности любых измерений существует и известна. Будем считать, что эта техника в любой области соблюдена.
Результат (само свойство):
При соблюдении нужной техники (своей для естественнонаучных, технических и своей для гуманитарных знаний) обеспечивается точность измерений. Поэтому данные в МД, независимо от типа переменных, считаются в равной степени точными.
3). Сравнение числовых и качественных значений
1 .Доводы сторонников неравноправия числа и слова:
а) численные значения выше качественных, так как:
- числовые значения однозначны и законы их преобразования точны,
- исторически власть числа увеличивается.
б) качественные значения выше количественных, так как:
- в основе количественных лежат аксиомы, выраженные на ЕЯ, т.е. качественные,
- преобразование качественных значений в количественные почти всегда сопровождается погрешностями,
- качественных значений больше.
2.Доводы сторонников равноправия числа и слова:
а) типы переменных соответствуют специализации полушарий головного мозга (это подтверждают сведения из физиологии и анатомии)
б) в истории человечества просматривается переход от симметрии мозга к асимметрии и к рождению, как естественного языка, так и числа (это подтверждается сведениями из лингвистики и этнографии)
О слове в ЕЯ и знаке в формальных языках:
1). ЕЯ пронизан понятиями, обозначающими субъект "Я". Это
"Я" находится в центре пространства-времени ЕЯ. Это называется
”общечеловеческой субъективностью”. Исторически слову "Я"
предшествует соответствующая песня, которая есть у первобытных
народов. Глубинную основу ЕЯ составляет восприятие
(правополушарное), а грамматика и число относятся к левому
полушарию. ...
2). Слово многозначно и значения слов не разграничены резко - это называется "свобода в порождении слов". Благодаря этому разные люди понимают друг друга, несмотря на различия индивидуальных опытов, и непонимание возникает при попытке разграничить слова.
3). Недостатки формальных языков: искусственные логические языки, в частности математический, обладает предельной однозначностью. Они содержат ограничения, проявляющиеся в логических парадоксах. Их изучал Б.Рассел. В каждом формальном языке существуют такие предложения, что их истинность или ложность, в рамках этого языка, доказать нельзя (теорема Т. Геделя).
В результате получаем такие свойства:
Специализация полушарий мозга, необходимость общения людей, достоинства и недостатки формальных языков, погрешности преобразования слов в числа и наоборот (см. ниже) приводят к неизбежности сосуществования числа и слова.
4). Погрешности преобразования типов значений переменных. Классифицируем погрешности.
Считаем, что выраженный в качественной форме, конкретный вопрос и ответ, если он истинный, являются адекватными обстоятельствам и абсолютно точны. Традиционно считается, что для обеспечения точности надо от качественных значений признаков перейти к количественным их значениям и дальше ими оперировать. Затем в конце от числа перейти к качественному значению ответа, но при этом вводятся погрешности.
Рассмотрим виды погрешностей на примере утвердительного суждения или высказывания:
1). Есть первичное точное высказывание: "на улице 30°С”, если преобразовать его так: "на улице градусов 40°С", то будет погрешность, которая называется числовое огрубление числового значения.
2). Есть точное высказывание: "сегодня 30°С, а вчера было 27°С", при преобразовании: "сегодня жарче, чем вчера или сегодня также как вчера" внесем погрешность, которая называется качественное огрубление числового значения.
3). Первое точное высказывание: "сегодня многим на улице душно", и второе точное высказывание: "если душно, то много легко одетых". Хотим воспользоваться умозаключениями по Аристотелевскому силлологизму:
рыба дышит жабрами
карп - рыба => Заключение: карп дышит жабрами.
Применяем кванторы аристотиевских силлогизмов: (
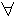 и
и 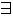 )
)Тогда из первого точного высказывания применяем
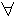 : сегодня всем на улице душно – получаем: это точно.
: сегодня всем на улице душно – получаем: это точно.Или применяем
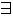 : существуют такие, кому душно.
: существуют такие, кому душно.Получаем вместо второго точного высказывания, аналогичные два возможных
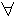 : если душно, то все легко одеты. – это логично.
: если душно, то все легко одеты. – это логично.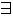 : если душно, то существуют легко одетые. – это влечет степень не точности.
: если душно, то существуют легко одетые. – это влечет степень не точности.Ясно, что заключения будут неточными.
4). Точное высказывание ("Сегодня многим на улице душно") преобразуем в ("Сегодня на улице градусов 30°С"). Вносим погрешность, ее составляющие:
замена многомерности понятия одномерностью, т.к. в понятии “душно” есть влажность воздуха, в чем одета и т.д.
неоднозначность и ограниченность перевода в число (например, можно выразить в другой системе)
Это количественное огрубление качественного значения, хотя можно привести примеры того, что в некоторых пределах погрешность не вносится.
5). Преобразования нужны для дальнейшей обработки в логике и в численной форме, и аппарат обработки вносит свою погрешность. Когда логическую обработку делает человек, то его рассуждения грешат против логики. Показано, что из 512 силлологизмов верными являются 24, а люди в своих интересах используют любые, поэтому естественно желание применить огрубление на входе, зато безошибочно вести числовой анализ, но возникает погрешность, одна из составляющих - это погрешность интерпретации в качественных значениях числового результата.
Результат:
Нежелательно преобразование типа значения переменных ввиду неизбежности погрешности преобразования.
Выводы:
1). В данном курсе математикой должны считать способы обращения с обозначениями, которые обеспечивают точность в данный предметной области.
2). Язык, на котором можно обсуждать и доказать положения в равной мере относящиеся к количественным и качественным значениям, - есть ЕЯ.
Тема 11. Детерминация. Диаграммы Венна.
Существенность аргументов.
Рассмотрим выражение:
a=>b (l)
I= ,C=
Обозначим:
P(b/a) – условная частота (доля) объектов, обладающих свойством “b” среди обладающих свойством “а”.
Р(a/b) - условная частота (доля) объектов, обладающих свойством “а” среди обладающих свойством “b”.
Такая запись (1) называется детерминацией, если в ней а и b – это выбранные свойства (значения разных признаков по МД),
Р(b/а) - точность детерминации (1) и обозначается I (a=>b);
I (a=>b) = Р(b/а)
Р(а/b) - полнота детерминации (1) и обозначается С(а=>b);
С(а=>b) = Р(а/b).
а - аргумент детерминации,
b - функция детерминации, стрелка “=>” читается: “следует”.
Точность и полнота легко подсчитываются по таблице сопряженности выделенных признаков, которая следует из МД.
Рассмотрим простую таблицу сопряженности х и у:
| у | | | |
| у≠b | 60 | 590 | |
| у=b | 140 | 210 | |
| | х=а | х≠а | X |
N = 60, 590, 140, 210 – число объектов, которые обладают соответствующей парой свойств. (например 590 объектов таких, что у них у≠b и х≠а).
Получили следующую точность и полноту высказывания:
I(a=>b) = P(b/a) = N(ab)/N(a) = 140/200 = 0,7
C(a=>b) = P(a/b) = N(ab)/N(b) = 140/350 = 0,4,
где N(ab), N(b), N(a) - числа объектов, обладающих
свойствами а и b сразу, т.е. где: y=b, - x=a. .
Получается, что из а следует b с точностью I = 0,7 и полнотой
С = 0,4.
I = 0,7 - характеризует истинность высказывания из “а следует b”, т.к. дает долю случаев из а, в которых оно истинно.
С = 0,4 - характеризует полноту высказывания из “а следует b”, т.е. долю случаев реализации значений b, которая следует из а.
Если бы обе величины I и С были бы равны 1, то могли бы сказать, что в любом объекте для того, чтобы у = b необходимо и достаточно, чтобы х = а.
Свойства детерминации
1). Детерминации существуют, если N(a) и N(b)≠0
2). Детерминации соответствуют 2 зрительных образа: это строка и столбец таблицы сопряженности, где фигура есть свойства а и б и выделяется функция:
а)
| у≠b | | |
| y=b | | |
| | х=а | х≠а |
б) Диаграмма Венна с выделенной функцией (например b)
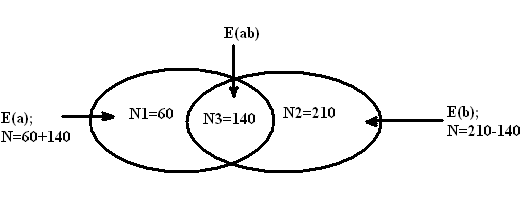
3). Точность и полнота изменяются от 0 до 1 и полнота от 1 до 0.
4). I и С практически независимые характеристики. Если I или С равны 0, I/C = 0, то и С/I = 0, но кроме нулевых значений характеристики независимы.
Характерные диаграммы Венна:
a) Неточная неполная детерминация.
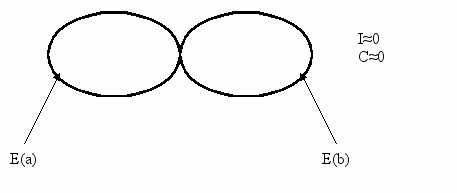
б) точная неполная детерминация
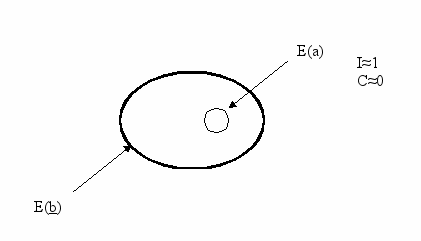
в) неточная полная детерминация
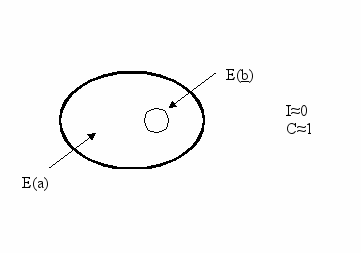
г) Полноточная детерминация
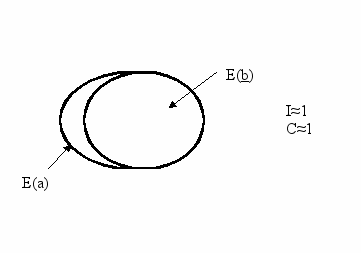
5). Бывает обратная детерминация это b=>а (обратная к (1))
В ней I2=C1
C2=I1
6). Индивидуальная (нулевая) и универсальная (единичная) переменная.
Введем “Заданное основание” – численность групп объектов. На основе МД, можно ввести нулевую «е» и единичные «ω» переменные с помощью равенств по основанию.
ex = e (3)
ωx = x (4)
Понятие, которое стоит за переменной е - это конкретный объект, а за ω - совокупность исследуемых объектов как целое.
Уточнение. Существенность аргументов.
Рассмотрим две детерминации
a=>b
I1,C1, (1)
am=>b
I2,C2. (2)
Т.е. в (2) имеется дополнительное свойство m. Возможны следующие случаи:
I2>,=,
Введение m и изменение точности интерпретируется двояко:
1). уточнение, которое m вносит в детерминацию (1).
2). уточнение, которое m вносит в детерминацию (2).
Уточнение называется положительным, если I2 > I1, отрицательным, если I2 < I1 и нулевым, если I2 = I1 .
Положительное или отрицательного уточнение называется
существенным, а нулевое несущественным. Мерой существенности уточнения является приращение точности, которое/ происходит при включении m в детерминацию (1).
Рассмотрим в качестве примера:
| Y | | | | | |
| В | 0 | 60 | 100 | 40 | |
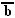 | 100 | 40 | 0 | 60 | |
| | am | 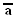 m m | a 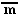 | 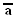 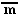 | xv |
У,х
| y | | | |
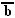 | 100 | 100 | |
| В | 100 | 100 | |
| | a | 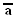 | X |
y,v
| Y | | | |
| b | 60 | 140 | |
| В | 140 | 60 | v |
| | m | 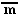 | V |
Согласно таблице I1=I (a=>b) = 0.5,
I2 = I (am=>b) = 1
S (am*b) = I2 - I1 = 1-0.5 > 0
S-существенность, a * - отличительное свойство, которое производит уточнение (в данном случае это m)
S = 0.5 - это есть существенность свойства m.
Существенность свойства а:
S (a*m=>b) = I (am=>b) -I (m=>b) = 1-0.7 = 0.3
Свойство m более существенно, чем свойство а для b.
Контекст
Любое утверждение справедливо лишь в определенном контексте. Универсальные свойства для МД определяются универсальным контекстом.
Пример:
Если исследуются сельские жители данного региона, то за "ω" стоит (сельские жители данного региона). Если потом исследуются и сельские и городские жители, то будет новый универсальный контекст "ω" - житель данного региона, а старый контекст перестает быть универсальным, становится обычным свойством, наряду с другими. Изменение контекста изменяет величины I и С.
Перейти в контекст k - значит перейти к рассмотрению только группы еk, а прочее исключить из рассмотрения, при этом переменные a=>ak, b=>bk, и высказывание ak=>bk.
Результаты:
1). Добавляя свойство в аргумент (из а в аk), можно повысить, не изменить или понизить точность, а добавляя свойство в функцию, можно сохранить или повысить полноту, а контекст может увеличить и точность и полноту.
2). Самым широким контекстом высказывания а=>b является контекст "со", но его S=0. Самым узким контекстом этого высказывания является индивидуальный контекст "е", при этом I и С равны 1, но в самом высказывании не будет особенного смысла.
е(а=>b) = (е=>b), т.е. изучать связи между свойствами имеет смысл в достаточно широких контекстах.
Обобщения и ДА при решении практических вопросов.
§1.Детерминизм и статистичность. Ограниченная статистичность и функция.
Точность и детерминизм. Точность I (a=>b) является мерой статистического влияния свойства (события) a, на свойство (событие) b. Влияние максимально при I=1, тогда ситуация соответствует детерминизму, т.е. предопределенности b при наличии а, их связывает функция b = f (a)
Статистичность то есть отсутствие детерминизма можно измерять разностью:
1-I (а=b)
- I >= η> 0.5, это случай ограниченной статистичности
- при I (а=>b) = 0, статистичность максимальна и минимально влияние а на b
- крайнее значение I (1 и 0) в гуманитарных знаниях при любом а и b из-за проявления свободы воли человека, а практически интересны только сильные влияния одних свойств на другие, т.е. практически интересует ограничение статистичности.
Детерминации определены при всех I, а функциональная связь только при I=1, следует, что детерминация - обобщение функции.
§2.Детерминация и статистическая связь
Детерминация является единственным показателем направленной статистической связи свойств. При этом связь понимается как приближение к детерминизму, т.е. к возможности делать предсказания и объяснения типа: из х=а следует, что у=b.
§3.Полные и неполные объяснения и предсказания.
О детерминации а=>b, при I≈1, можно сказать, что b объясняется значением а, с другой стороны, если х=а, то для него можно предсказать значение у=b. Объяснения и предсказания характеризуются величиной полноты C:
- при C≈ 1, говорим о полном объяснении и предсказании,
- при малых C, говорим о неполном объяснении и предсказании
Полные объяснения и предсказания отличаются от неполных психологически и практически.
Какова детерминация в примере из Темы 9:
a=>b, где
I1,C1
х = а - смерть от рака легких
х =
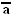 - смерть не от рака легких
- смерть не от рака легкиху = b - человек курил
у =
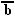 - человек не курил.
- человек не курил.Тогда детерминация а => b с характеристиками (I1,С1) означает: “если человек умер от рака легких, то он курил”. Здесь точность I1 - велика, т.к. рак легких редко бывает у некурящих людей.
Воспользуемся тем, что С1 = I2, т.е. точности такого высказывания: b=>a (I2,C2). “если человек курил, то он умер от рака легких”. Точность I2 этого высказывания мала, т.е. и С1 мало, поэтому детерминация: “если человек умер от рака легких, то он курил” является точной и неполной. На что это сказывается: Неполнота снижает действие предосторожности от курения. Т.е. нужно стремиться не только к точным, но и полным детерминациям.
§4.Априорные и апостериорные обобщения
Для обеспечения точности измерений необходимо, чтобы опытные признаки выражались в свойствах, в которых проявляет себя объект. Это приводит к дробности описания в первичных элементах МД. Для теоретического осмысления и применения необходимо обобщение полученных результатов. Обобщения бывают априорными и апостериорными.
Пример:
Пусть X1 - наличие или отсутствие автомобиля Х2 - наличие или отсутствие компьютера Х3 - наличие или отсутствие стиральной машины у - априорное обеспечение техникой
Введем априорное обобщение по у:
у = (высокое, среднее, низкое)
высокое - все 3 предмета,
среднее - 2 предмета, низкое – 1 предмет.
Тогда получим вторичную переменную
у = f0(Х1,Х2,Х3)
А если при измерениях ввести признак апостериорной обеспеченности z:
z = (высокое, среднее, низкое, затрудняюсь ответить)
z = fl(Xl,X2,X3)
В априорном обобщении есть наш произвол, а в апостериорном обобщении проявляются свойства объектов.
Замечания:
Априорное понятие (низкое, высокое, и т.д.) есть огрубление апостериорного качественного значения априорным качественным значением. Этот вид погрешности нами рассмотрен. Программа исследования на ДА-системе зависит от цели, а результат всегда представляется в виде текста на языке очень близком к ЕЯ и содержащим значения признаков.
§5. ДА и практические вопросы
Рассмотрим практические вопросы с точки зрения ДА программы:
из предпосылок => результат
То, что при формулировке вопросов называется результат, будем рассматривать как множество значений функций соответствующих детерминации, а предпосылки как аргумент детерминации у нас были сформулированы практические вопросы.
Вопросы:
1). Предсказание результата исходя из существующего
положения как предпосылок.
Решение заключается в уточнении контекста и определении множества существующих предпосылок Е(а) = (al, a2, ...an)
Достаточно точных детерминаций, связывающих эти предпосылки с возможными результатами (функциями) этих детерминаций.
Э
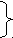 то: a1=>b1
то: a1=>b1a2=>b2 точные детерминации.

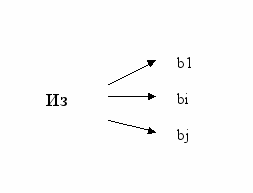
2). Поиск путей, приводящих к нужному результату.
Это определение множества аргументов достаточно точной детерминации с известной функцией.
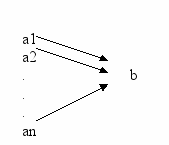
3) и 4)вопросы
Выработка понятий наиболее адекватных для описания предпосылок или функций.
Это есть задача введения вторичных переменных для аргументов или функций
Пример:
Данные первичных переменных: Зарплата 1000, 1500, 2000 вторичные данные: Зарплата 1000 - 2000
5). Объяснение некоторых положений в настоящем или прошлом.
В первичных признаках этот вопрос означает включение свойств, характеризующих объясняемые положения в характеристику функций достаточно точных детерминаций, аргументы которых можно найти среди характеристик положения. Для объяснения на обобщенном уровне нужно сделать тоже самое, но со значениями вторичных переменных.
6). Пока не может быть решен.
Результат:
При помощи ДА пять практически важных для организма вопросов могут быть решены на логическом уровне. У кого есть программа РА, они могут на этом уровне решать свои практические задачи.
Тема 13. Межмассивная обработка данных. Знакомство с детерминационной силлогистикой.
Введение:
Будем применять следующий общепринятый словарь «Словарь физики Логоса:
Строка в МД - это опытный образ объекта.
Столбцы в МД - это признаки.
Значение признака - это свойство объекта.
Эйдос - множество значений в клетках МД, имеющие одно
(общее) значение признака.
| | Признак x | Признак y | | Признак c |
| Объект 1 | a | b | | c |
| Объект 2 | 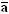 | b | | 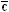 |
| Объект 3 | 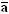 | 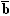 | | c |
| … | a | b | | c |
| … | a | b | | c |
х = а - один эйдос, его множество Е(а), объем N(a).
у = b - другой эйдос, его множество Е(b), объем N(b).
z=c – третий эйдос, его множество Е(с), объем N(с).
Детерминация (по-другому) двух эйдосов.
Образ - это эйдос единичного объема или клетка в МД.
Логос -это:
- мир эйдосов, по другому:
- эйдос, занимающий весь столбец в МД.
§1. Межмассивная обработка данных и задача обобщения
силлогизмов.
Остался нерешенным 6 практический вопрос: "В какой мере верно считать, что из х = а, у = b следует, что z = с, если знаем характеристики следования а=>b и b=>с, а нужно узнать характеристики, следования а=>с?"
Характеристики - полнота и точность взаимодействия двух эйдосов.
Этот вопрос относится к взаимодействию трех эйдосов, а практическим он является, т.к. часто встречаются два опыта (в одном задействованы характеристики х и у, а в другом опыте задействованы у и z). Сделать обследование, в котором задействованы х и z, исключается, например, по причине дороговизны. Поэтому установление характеристик а=>с является вопросом межмассивной обработки данных.
Пример:
a

 =>b, b=>c a=>c
=>b, b=>c a=>c(I1,C1) (I2,C2)
 (I,C-?)
(I,C-?)- - логическое следование (силлогизм)
(1)- частная форма записи, необходимо обобщить запись, чтобы были все формы 3-ех эйдосов:
(a=>b, b=>c)
 ( с=>а) - всего таких форм 8.
( с=>а) - всего таких форм 8.В некоторых предположениях (1) становится общим видом записи связи 3-ех эйдосов,
Далее нужно обобщить:
1). Аристотелевский контекст
2). Аристотелевские квантификаторы
"а" = "все ...есть..." ≈ {1}
"е'= "не ...не есть..." ≈ {0}
"i" = "некоторые...есть..." ≈ (0;1]
"о" = "некоторые...не есть" ≈ [0;1)
В этих предположениях Аристотель рассматривал всего 256 силлогизмов. В некоторых предположениях можно считать, что он рассматривал 512 силлогизмов, из которых 24 верных.
Pω1 (a) = N(a ω1)>0 / N
Pω2(b) = N(bω2) / N
Рω3(с) = N(c ω3) / N
ω - контекст
Р..(..) - относительные частоты соответствующих эйдосов
N - объем Логоса
N(...) - объем эйдоса в контексте ω
Относительные частоты не превосходят:
0
Аристотель
рассматривал только
такие контексты
< Pω1(a)< = 1
0 < Pω2(a)< = 1
0 < Pω3(a)< = 1
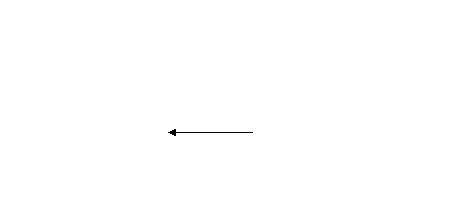
А общий случай контекста заключается в произвольном ограничении относительных объемов внутри единичного полуинтервала (0;1].
Мы получили следующую запись детерминационного силлогизма:

 a=>b, , b=>c c=>a
a=>b, , b=>c c=>aK=[r1,2;s1,2] L=[r2,3;s2,3]
 R=[r1,3;s1,3] (*)
R=[r1,3;s1,3] (*)M=[r2,1;s2,1] N=[r3,2;s3,2] S=[r3,1;s3,1]


A B
[ri,j;si,j]
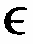 δ=[0;1]
δ=[0;1]Ω=Ω1 ([ω1, Ө1]; Ω2[ω2,Ө2]; Ω3[ω3,Ө3])
ωj >= ε = 1/N
i,j=1,2,3…- номера детерминации
Обозначения:
r
 i,j - левый конец отрезков, выражающих обобщенные квантификаторы:
i,j - левый конец отрезков, выражающих обобщенные квантификаторы:si,j - правый конец отрезков, значения точности и полноты.
Ω - обобщенный контекст.
ω
 1 – левый конец отрезков, выражающих ограничения на
1 – левый конец отрезков, выражающих ограничения на Ө1 - правый конец отрезков, безусловные частоты эйдосов.
N – объем логоса.
ε – квант относительных частот.
Сокращенная запись детерминационного силлогизма:(*) А
 В Исследования детерминационного силлогизма (*) означает решение задач, стоявших перед Аристотелем, т.е. найти все силлогизмы и найти из них те, которые правильные.
В Исследования детерминационного силлогизма (*) означает решение задач, стоявших перед Аристотелем, т.е. найти все силлогизмы и найти из них те, которые правильные.§2.Проблема 3-ех эйдосов
Постановка проблемы:
В силлогизме A – посылка, а B – заключение
Даны условные посылки
a
 b , bc
b , bc r1,2 P(b/a) s1,2; r2,3 P(c/b) = s2,3 = A
r2,1 P(a/b) = s2,1; r3,2 P(b/c) = s3,2
