Корзинкин Владимир Анатольевич Москва 2009 литература
| Вид материала | Литература |
- Веткин Владимир Анатольевич, кандидат физико-математических наук, доцент Винтайкина, 3941.49kb.
- Тэк сегодня среда, 25 февраля 2009 г. Часть 2 содержание, 828.56kb.
- Владимир Анатольевич Беляев (Помощник председателя), Муромский историко-художественный, 44.04kb.
- Маталасов владимир анатольевич, 1108.96kb.
- Хохлова Галина Ивановна. "Возможности разработки идеологии научного сообщества"., 12.17kb.
- Зеленский Владимир Анатольевич, начальник отдела консолидированной отчет, 598.05kb.
- Название дисциплины, 587.61kb.
- Фисинин Владимир Иванович Доктора наук Габитов Ильдар Исмагилович Зыкин Владимир Александрович, 2780.59kb.
- Маяковский Владимир Владимирович. Маяковский Владимир Владимирович (1893, с. Багдади, 59.82kb.
- Князья Владимир Святославич, Ярослав Мудрый, Владимир Мономах. 11. Культура Древней, 24.41kb.
Нужно найти границы точности и полноты заключения или 3-ей детерминации: (ac) ?
a
c± P(c/a) ?
± P(a/c)
0 1
0 1
Нужно найти границы точности и полноты, т.е. детерминации ac так, чтобы в силлогизме А
В всегда, когда A – истинно (в смысле характеристики находятся в заданных границах), B – было бы истинным (т.е. ее характеристики находились в пределах ; , ; Замечание: Если произвольно задать характеристики 3-ей детерминации, то могут быть случаи несуществования и ложности. Ложность, когда ac существует, но не в заданных границах.
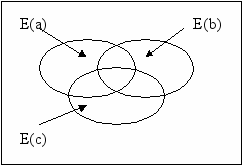
Несуществование:
E(a)
E(b)
E(c)
Общий случай существования обобщенного силлогизма:
X7
X5
X6
X3
X1
X2
X6
Трехмерная таблица сопряжения признаков:
| a | X1 | X2 | X3 | X4 |
| a | X5 | X6 | X7 | X8 |
| | B | b | b | b |
| c | c | |||
8
xi = N,
i=1
i, xi 0,
xi – объемы множеств.
Для случая существования, как следует из определения точности и полноты,
P(c/a) = (x1+x2)/(x1+x2+x3+x4)
P(a/c) = (x1+x2)/(x1+x2+x5+x6)
Искомые границы выражаются так:
+- = max, min P(c/a)
+- = max, min P(a/c)
По поводу решения: Решение поставленной проблемы может быть сведено к
“
задаче “ дробно-линейного программирования Л.В. Конторовича в 8-мимерном пространстве.§3.Формы решения
В принципе могут быть аналитическими и числовыми. Аналитический промежуточный результат для такого случая:
приведен в литературе.
1 = 1 =
2 = 2 =
3 = 3 =
В этом частном случае мы получаем выражение из 20-ти областей, на которых определены 40 функций. А общий случай, когда для каждого i, i i настолько громоздкий, что и в журнальных статьях не приводится. Выражение имеет смысл использовать в ЭВМ, применяя стандартную программу симплекс-метода.
§4. Примеры истинных детерминационных силлогизмов.
Рассмотрим 2 детерминационных силлогизма в сокращенной записи.
Т
очность K L RП
олнота M N S 
- 1 1 1
= ( ,1; ,1; ,1 ) =1/N
(2) 1,1 1,1 υ, 1
= ( ,1; ,1; ,1 )
Оба силлогизма (1) и (2) можно рассматривать вместе, если ввести запись в такой форме:
(3) r1,2; s1,2 r2,3; s2,3 r1,3; s1,3
- r
2,1 = r3,2 = 0
s2,1 = s3,2 =1
Для случая (3) в литературе 1990г. имеется полное решение, т.е. когда i i и это решение дает:
- = min ( …в обл….)
+ = max ( …в обл….)
- = min ( …в обл….)
+ = max ( …в обл….)
получается всего 36 формул, содержащихся в этом решении, из этих формул получается следующее:
Cиллогизм 1 может быть записан так:
ab bc ac
1 1 1
в контексте
= ( 1/N ,1; 1/N,1; 1/N,1 )
Одна из общепринятых лингвистических формул контекста такова “существует хотя бы по-одному a, b и c”. В этих условиях имеет место силлогизм 1. Одна из принятых лингвистических форм его прочтения такая: «Из того, что “все a – суть b” и “ все b – суть c” следует, что “ все a – суть c”»
Это известный силлогизм Аристотеля “AAA” и он означает:
Если “все а суть b”, и “все b суть c”, то “все a суть c”
Полнота здесь может быть любой.
Например, у нас было:
c – дышать жабрами
b - рыбы
a - карпы
