Тематический план введение

Вид материала

Тематический план

Содержание Вопросы для самоконтроля Сравнительная характеристика mathcad Тренинг умений Внимание! Место набора символа помечается синей рамкой. Двигать рамку следует клавишей пробела. Пояснение. Аргументы логарифмической и тригонометрической функций следует заключать в круглые скобки. Учебное издание

Подобный материал:

• Учебно-тематический план занятий, 452.3kb.
• Тематический план. Тематический план для очной формы обучения, 116.28kb.
• Д. Ю. Кузьмин Приказ № от 2009 г. Тематический план, 30.83kb.
• Тематический план по спецкурсу «Протокол и этика делового общения» для студентов, 32.43kb.
• В. Е. Гущев 2010 г. Тематический план, 22.07kb.
• В. Е. Гущев 2010 г. Тематический план, 32.7kb.
• Тематический план Тематический план для очного обучения (2 семестр), 791.32kb.
• Тематический план по дисциплине «Экономическая теория», 27.93kb.
• Н. И. Толочанов А. А. Перспективно тематический план, 1034.48kb.
• Борбат Нина Александровна января 2011 г подпись И. О. Ф. число, месяц календарно-тематический, 82.51kb.

Вопросы для самоконтроля

1. Встроенные функции MS Excel, их назначение и классификация
   
2. Встроенные функции MS Excel, используемые в экономике
   
3. Статистические встроенные функции Ms Excel
   
4. Выборка и анализ данных в MS Excel
   

5. СРАВНИТЕЛЬНАЯ ХАРАКТЕРИСТИКА MATHCAD
   

И MICROSOFT EXCEL


В настоящее время для рутинных расчетов на компьютере чаще используются не традиционные языки программирования (Basic, Pascal, Fortran) а электронные таблицы и специальные математические программы. Говоря об электронных таблицах, мы обычно имеем в виду Microsoft Excel. Математическая же программа у нас часто ассоциируется в основном с пакетом MathCad. Оба эти пакета задумывались как средства работы на компьютере пользователей, не желавших или не умевших «возиться» с языками программирования при решении финансовых, научно-технических и прочих прикладных задач (программирование без программирования).

MathCad – это гибкий инструмент для математических, инженерных, научных и финансовых вычислений более высокого уровня, чем электронные таблицы, так как он создавался на основе электронных таблиц.

В последних выпусках MathCad видна устойчивая тенденция к тесной интеграции с общераспространенными настольными приложениями. В отличие от других высокофункциональных пакетов, например Mathematica, которые выполняют роль основного инструмента специалиста, MathCad вполне пригоден и в качестве вспомогательного средства. Так, пользователь, которого не удовлетворяют графика или программистские возможности Microsoft Excel, может использовать более мощные средства MathCad, предоставляющего вместо жестких сеток Excel среду для создания сложных документов.

Ядро MathCad напоминает рабочую тетрадь с интерфейсом в стиле текстового редактора и имеет готовые инструменты для числовых и символьных вычислений и построения графиков, дающие в совокупности гораздо более мощные и гибкие возможности, чем электронные таблицы.

MathCad обладает несравнимо более высоким потенциалом в сфере обработки экспериментальных данных (интерполяции, регрессии, экстраполяции), поэтому, даже если результаты измерений были записаны в виде электронной таблицы, строить на их основе графики и диаграммы лучше в MathCad.

Технология работы в средах Microsoft Excel и MathCad имеет много общего. Так, процесс создания «программы» идет параллельно с ее отладкой и оптимизацией. Отладочные фрагменты (не только числа, но и графики, а также анимационные клипы) можно оставить в готовой таблице или в MathCad-документе для того, чтобы убедиться в правильности хода решения задачи. В Microsoft Excel и в MathCad встроено большое количество математических операторов и функций. И в среде Microsoft Excel, и в среде MathCad математический аппарат можно расширять, создавая пользовательские операторы, функции и процедуры.

Следовательно, в силу своей схожести, эти пакеты могут работать совместно. Экспортировать данные из таблицы Microsoft Excel в матрицу MathCad можно просто скопировав их и вставив затем в пустую таблицу ввода. Однако провести обратную операцию, то есть данные из матрицы MathCad экспортировать в Microsoft Excel, используя таблицу ввода, невозможно. Для выполнения этой задачи следует задействовать таблицу Microsoft Excel как компонент MathCad.

Идея совместной работы реализована в среде программы MathConnex, входящей в состав MathCad. MathConnex позволяет интегрировать различные приложения Windows (Excel, MathCad, MatLab, Axum) и организовывать передачу данных между ними.

На рабочем столе MathConnex находятся три компоненты: вверху – электронная таблица Excel с одним выходом; в середине – MathCad-документ (там комментарии прописаны ярким шрифтом, а рабочие формулы – блеклым) с одним входом и одним выходом; одна электронная таблица Excel внизу с одним входом.

Входы и выходы компонент пользователь соединяет линиями с помощью протяжки мышью. При создании рабочего листа MathConnex (а это делается довольно просто: нажимается кнопка с пиктограммой соответствующей компоненты, и «перетаскивается» на рабочий лист) в результате появляются диалоговые окна для задания параметров компонент. Одно из таких окон, работая с которым пользователь задает число входов (Inputs) и выходов (Outputs) у электронной таблицы, связывает с ними области ячеек.

Вставляя электронную таблицу Excel в рабочий лист MathConnex, пользователь может либо создать новую таблицу, либо взять готовую из архива.

В среде MathCоnnex имеется 16 компонент (разбитых на 4 группы):

1. Ввод и вывод данных:
   

• ввод локальных констант, можно обойтись без верхней Excel-таблицы, вводя исходные данные (константы 138, 540, 5 и 3) прямо в MathCad-компоненту;
  
• ввод глобальных констант – констант, доступных во всех компонентах;
  
• чтение (запись) данных из файлов на дисках;
  
• генерирование последовательностей (значения переменной, линейно меняющейся в заданном диапазоне с заданной скоростью), эта компонента незаменима при моделировании динамических процессов, ею можно, к примеру, задавать течение времени.
  

2. Просмотр результата:
   

• «инспектор» – эту компоненту обычно вставляют на линиях для контроля потоков данных;
  
• график MathConnex (не просто график, а скорее осциллограф, позволяющий визуализировать динамику изменения неких величин);
  
• график Axum (графики можно построить и в Excel- и MathCad-компонентах.
  

3. Вычисление:
   

• MathCad;
  
• Excel;
  
• MatLab;
  
• калькулятор MathConnex – его используют для небольших вычислений, когда не имеет смысла задействовать один из вышеперечисленных «монстров» – Excel, MathCad или MatLab.
  

3. Управление потоками данных:
   

• выключатель;
  
• слияние потоков;
  
• разветвитель по условию;
  
• стоп/пауза.
  

MathConnex – это одно из средств визуализации OLE2-технологии. Раньше такие программно-апаратные средства решения задач назывались системными интеграторами. Они предназначены, в том числе, и для ситуационного моделирования. Аналогичные функции выполняет MathConnex только уже на качественно ином уровне. MathConnex – это виртуальная аналоговая вычислительная машина (АВМ), точнее, гибридная ЭВМ, на которой можно проводить работы по математике, физике, химии, теории автоматического регулирования и т.д. При этом пригодятся наработки, созданные и в среде MathCad, и в среде Microsoft Excel.

В настоящее время интеграционные процессы в среде программных продуктов различных фирм-производителей носят массовый характер, и тесное взаимодействие MathCad и Microsoft Excel лишь часть процесса создания единого мощнейшего программного продукта, который должен соединить в себе все наиболее необходимые пользователю функции и организовать их на должном уровне. MathCad и Excel, Promt и Word, Word и Fine Reader и многие другие разработки в области программного обеспечения имеют многоуровневую взаимосвязь. Без понимания принципов интегрирования различных программных продуктов современный пользователь лишается широких возможностей ускорения и упрощения работы на компьютере.


Вопросы для самоконтроля

1. Назначение и общая характеристика пакета MatLab
   
2. Структура пакета MatLab
   
3. Общая характеристика пакета Mathematica
   
4. Достоинства пакета Mathematica
   
5. Интерфейс пакета Mathematica
   
6. Общая характеристика пакета MathCad
   
7. Интерфейс пакета MathCad
   
8. Ввод формул
   
9. Работа с текстом
   
10. Встроенные функции MS Excel, их назначение и классификация
    
11. Встроенные функции MS Excel, используемые в экономике
    
12. Статистические встроенные функции Ms Excel
    
13. Выборка и анализ данных в MS Excel
    

Литература

1. Гурский Д., Гурский Ю. MathCad 2001 первые шаги: Компьютерная газета, № 37, 2 октября 2001г.
   

ГЛОССАРИЙ

№ пп	Понятие	Смысл понятия
	Math-документ	Электронный документ, поддерживающий на экране и на печати текст, формулы, и графику с цветом, массой шрифтов и символов, привычной двухмерностью математических обозначений и средствами формирования всего перечисленного, и анимацию со звуком
	Функции	Специально, заранее созданные формулы, которые позволяют быстро выполнять сложные вычисления

ТРЕНИНГ УМЕНИЙ


Умение первое: элементарные вычисления с помощью пакета MathCad


задание 1. Найти факториал числа 5.


Рекомендации по выполнению

1. Для выполнения вычисления следует вывести панель Арифметика:
   

Вид Панель инструментов Арифметика

2. Для нахождения значения факториала некоторого числа:
   

• нажмите на панели Арифметика символ [n!];
  
• в появившейся в рабочей области рамке наберите требуемое число 5;
  
• нажмите на этой же панели знак равно [=] (не путать со знаком присваивания [:=]).
  

После этих действий в рабочей области экрана получите искомый результат.

Внимание! Место набора символа помечается синей рамкой. Двигать рамку следует клавишей пробела.


задание 2. Вычислить следующие значения:

10^-2, 10³, ;

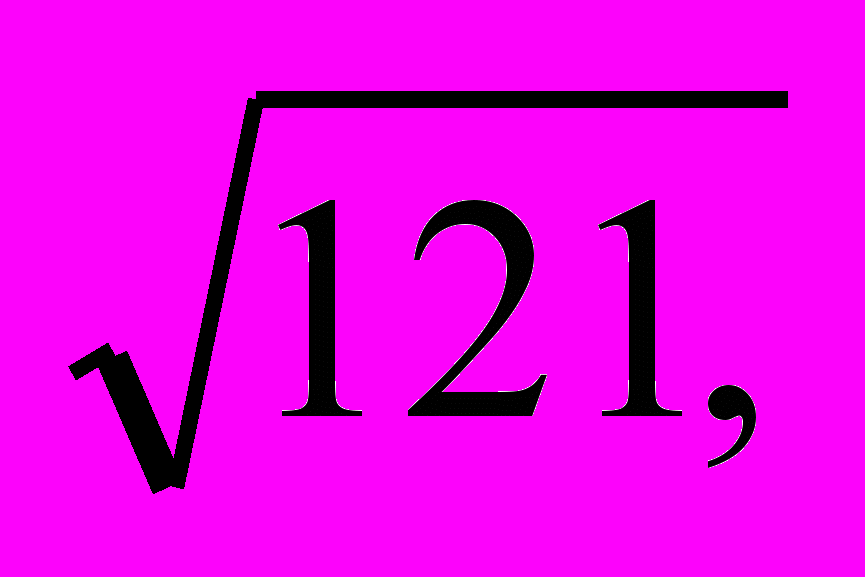
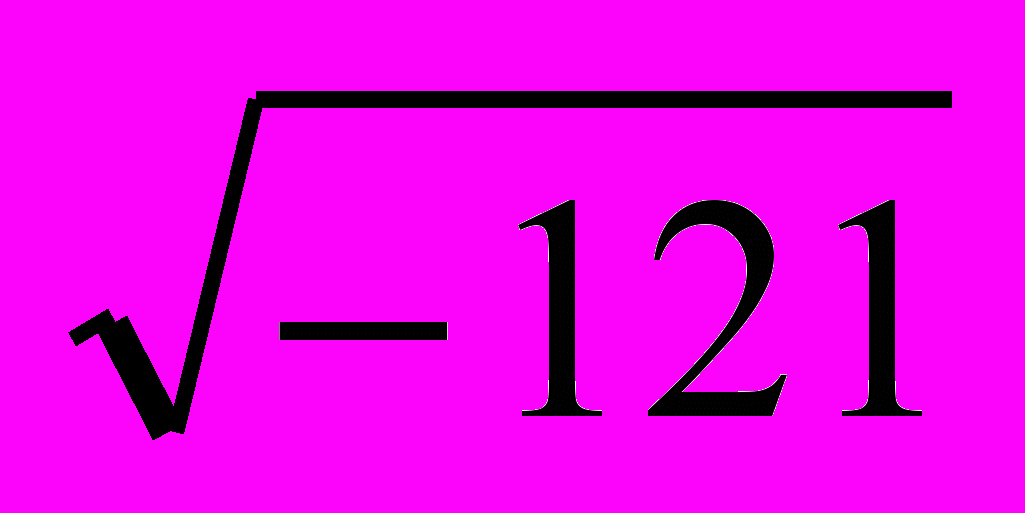log(1), log(-1), ln(0), ln(5);

sin(0), sin(1), sin(90);

cos(0), cos(1), cod(45);

tg(0), tg(180), tg(360).


Пояснение. Аргументы логарифмической и тригонометрической функций следует заключать в круглые скобки.


Умение второе: построение графиков с помощью пакета MathCad


задание 1. Построить график функции прямой f(x):=x. Определить значение функции при заданном значении аргумента.


Рекомендации по выполнению

1. Для построения графика прямой линии:
   

• наберите на клавиатуре, расположив в рабочем поле, требуемую функцию f(x):=x;
  
• нажмите клавишу [Enter];
  
• нажмите на панели Графики кнопку [Декартов график] – и в рабочем поле появится прямоугольник, представляющий собой декартовы координаты;
  
• напишите на оси абсцисс имя переменной х, а на оси ординат имя функции f(x);
  
• нажмите клавишу [Enter].
  

На экране появится график требуемой функции.

Пояснение. По Умолчанию система MathCad задает диапазон изменения аргумента от –10 до 10. Если вам необходимо изменить этот диапазон, то активизируйте график и измените значения диапазона слева и справа по оси Х.

2. Выполните редактирование построенного графика по вашему усмотрению, воспользовавшись правой кнопкой мыши. Например, измените толщину линии, выполнив команду:
   

ФорматСледТолщина

Выполните другие виды редактирования графика.


задание 2. Построить графики прямых линий:

y=2x; y=x+2; y=-2x; y=x-2; y=2x+2; y=-2x+2; y=2x-2.

Выполнить анализ поведения функции прямой линии в зависимости от углового коэффициента и свободного члена.


Внимание! Не забывайте в качестве имени функции указывать f(x), а не y, как в задании.


задание 3. Построить графики тригонометрических функций:

y=sin(x); y=sin(2x); y= -sin(x); y=sin(-x);

y=sin(x+2); y=sin(x-2); y=sin(x)+2; y=sin(x)-2;

y=cos(x); y=cos(2x); y= -cos(x); y=cos(-x);

y=cos(x+3); y=cos(x-3); y=cos(x)+3; y=cos(x)-3;

y=tg(x); y=tg(2x); y=2tg(x); y=tg(-x).


задание 4. Построить графики парабол:

y=2x²; y=-x²; y=(2x)²; y=-(2x)²; y=x²+5; y=(x+5)²


Замечание. При построении графиков 2-го порядка, таких как круг, эллипс, гипербола, на экране в рабочей области отражается лишь часть графика, расположенная выше оси х (то есть в положительной области изменения y).


Умение третье: приближенные вычисления с помощью пакета MathCad


задание 1. Получить значения функции y=5x+3 для х, изменяющихся от 0 до 10 с шагом 2.


Рекомендации по выполнению

1. Укажите требуемый диапазон и шаг изменения х, воспользовавшись кнопками [:=] и [m...n] на панели Арифметика. На экране должно появиться х:=0,2..10.
   
2. Наберите функцию f(x):=5x+3.
   
3. Выдайте на экран полученную таблицу значений функции, набрав f(x)=
   

Внимание! Набрать знак [=] (равно), а не [:=] (присваивания).

4. Выдайте на экран не всю полученную таблицу значений функции, а ее часть, воспользовавшись полосой прокрутки. Для этого выделите таблицу и переместите бегунок по появившейся полосе прокрутки, например, так, чтобы осталось только три строки.
   

Умение четвертое: операции над векторами с помощью пакета MathCad


задание 1. Выполнить операции над векторами:

• умножение вектора на число,
  
• скалярное произведение векторов,
  
• векторное произведение векторов.
  

Рекомендации по выполнению

1. Для умножения вектора на число
   

• вначале создайте вектор, набрав на рабочем поле V:=
  
• нажмите на панели Матрицы кнопку [Создать матрицу или вектор],
  
• в появившемся диалоговом окне Вставить матрицу укажите размерность вектора, например, Столбцы – 2 и Строки – 1 и нажмите на кнопку [OK],
  
• в рабочем поле в появившемся макете вектора укажите его конкретные координаты, например, 4 и 3 и нажмите на клавишу [Enter],
  
• умножьте созданный вектор на число, например, 5, выполнив действия:
  

U:=V ^ 5

• для отображения результата наберите U= и на экране появится
  

U = (20 15).


задание 2. Получите скалярное и векторное произведение векторов X=(2,2,2) и Y= (3,3,3). Найдите также сумму элементов каждого вектора.


Пояснение. Для определения скалярного произведения один из векторов должен быть строка, а другой – столбец. Для определения векторного произведения оба вектора должны быть либо строка, либо столбец.

Содержание

Введение.	3
1. Общая характеристика пакета MatLab.	4
2. Пакет Mathematica.	5
2.1 Общая характеристика пакета.	5
2.2 Достоинства пакета.	7
2.3 Интерфейс пакета.	9
2.4 О тех, кто делает пакет Mathematica.	10
3. Общая характеристика и интерфейс MathCad.	11
3.1 Общая характеристика пакета.	11
3.2 Интерфейс пакета.	15
3.3 Ввод формул.	15
3.4 Работа с текстом.	18
Реализация математических вычислений средствами пакета Microsoft Excel.	19
4.1 Встроенные функции Microsoft Excel.	19
4.2 Основные функции Microsoft Excel, используемые в экономике.	20
4.3 Выборка и анализ данных в Microsoft Excel.	23
5. Сравнительная характеристика MathCad и Microsoft Excel.	25
Литература.	28
Глоссарий.	28
Тренинг умений.	29

Учебное издание

Бородина Алла Ивановна

Крошинская Лариса Израйлевна

Сапун Оксана Леонидовна


Основы информатики

и вычислительной техники


Специализированные пакеты

для математической обработки данных


Редактор-корректор Л.Р.Рецкая

Компьютерная верстка О.Н. Якубович


Подписано в печать 08.10.2003 г.

Формат 60х84 ¹/₁₆. Печать офсетная. Гарнитура «Таймс».

Усл. печ. л. 2,07. Уч.-изд. л. 1,81. Тираж 100 экз. Заказ № 36.


НО ООО «БИП-С». 220004, г. Минск, ул. Короля, 3.

ЛВ № 251 от 18.03.2003 г.


Размножено на ризографе для внутреннего использования

БЕЛОРУССКИЙ ИНСТИТУТ ПРАВОВЕДЕНИЯ

Дистанционное образование


А.И.Бородина, Л.И Крошинская, О.Л.Сапун

ОСНОВЫ ИНФОРМАТИКИ

И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Специализированные пакеты

для математической обработки данных


Минск

2003