Блок 1: Рост стоимости вложений за счет присоединения процентов 4
| Вид материала | Анализ |
- Возмещение затрат по уплате процентов по кредитам и лизинговых платежей по договорам, 80.46kb.
- Правила определения таможенной стоимости товаров, действующие в рамках вто, 38.09kb.
- Биржевые спекулянты на российском фондовом рынке: в чем различия между новичками, 274.71kb.
- Капитального строительства, 96.76kb.
- В. А. Баумгертнер «Конкурентоспособность российских производителей минеральных удобрений,, 69.53kb.
- Ежедневный мониторинг сми 29 декабря 2011, 202.46kb.
- О реализации приоритетного национального проекта "Развитие апк в северных субъектах, 178.05kb.
- Темы рефератов по дисциплине: «Инвестиции» Принципы и методы оценки стоимости недвижимости, 147.42kb.
- Инструкция Возврат основного долга по кредиту осуществляется на счет №47422810300000000117, 61.51kb.
- Правила определения стоимости активов и величины обязательств, подлежащих исполнению, 58.04kb.
Модуль 3.
Оценка параметров потоков платежей
из книги "Техника финансовых вычислений на Excel" Смирновой Е. Ю.
Оценка параметров потоков платежей
В финансовой практике широко распространены контракты, предусматривающие не разовое, а систематическое движение средств – выплаты/поступления по заданному графику происходят регулярно.
Последовательность платежей, разделенных равными интервалами времени, называется равномерной финансовой рентой или потоком платежей. Поток платежей одинакового размера называется постоянной финансовой рентой или аннуитетом (англ. annuity). Если платежи неодинаковы по знаку и размеру, то применяется более общий термин денежный поток (от англ. cash flow).
Блок 5 посвящен методике математического дисконтирования денежного потока будущих доходов/расходов инвестиционного проекта и построенным на её основе критериям эффективности капиталовложений.
Блок 6 знакомит читателя с широко применяемым в финансовом анализе понятием аннуитета и возможностями автоматизации стандартных вычислений с использованием встроенных функций Excel.
БЛОК 5: Денежный поток инвестиционного проекта
из книги "Техника финансовых вычислений на Excel" Смирновой Е. Ю.

Денежный поток инвестиционного проекта
При изучении материала этого блока вы узнаете, что такое:
- дисконтированный доход;
- чистый дисконтированный доход;
- индекс рентабельности инвестиций;
- внутренняя норма доходности.
Методы измерения доходности инвестиционных проектов основаны на анализе равномерного денежного потока. Ожидаемые значения элементов денежного потока, соответствующие будущим периодам, являются результатом сальдирования всех статей доходов и расходов, связанных с осуществлением проекта.
Для приведения значений элементов денежного потока к сопоставимому во времени виду по выбранной норме дисконтирования оценивается суммарная текущая стоимость на момент принятия решения о вложении капитала, предшествующий началу движения средств. Уровень процентной ставки, применяемой в качестве нормы дисконтирования, должен соответствовать длине периода, разделяющего элементы денежного потока.
Чистый дисконтированный доход показывает, превышает ли текущая стоимость ожидаемых доходов/расходов по проекту (дисконтированный доход) инвестиционные затраты в начальный момент времени. В англо-американских учебниках по финансовому менеджменту этот показатель называется Net Present Value, поэтому формула его расчета, встроенная производителями вычислительной техники в компьютерные программы и даже в финансовые калькуляторы, стандартно идентифицируется аббревиатурой NPV.
Пример. Найти чистый дисконтированный доход1 проекта, требующего стартовых инвестиций в объеме 100 тыс руб., денежный поток которого задан рис. 41, по ставке сравнения 10% годовых.
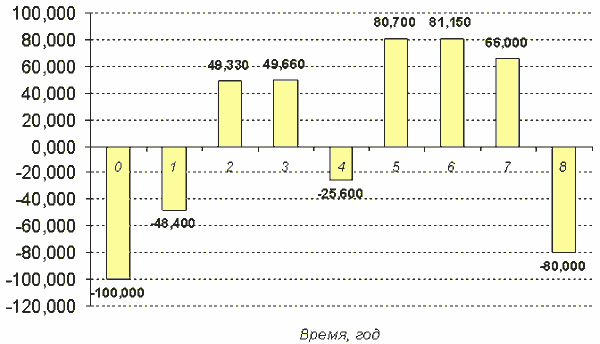
Рис. 41. Денежный поток проекта.
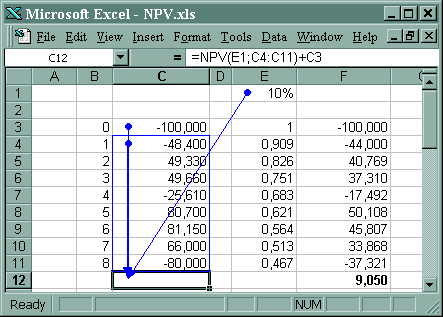
Рис. 42. Чистый дисконтированный доход.
Обозначим элементы денежного потока Z1,Z2,…,ZN в соответствии с моментами времени, а инвестиционные затраты нулевого периода – Z0.
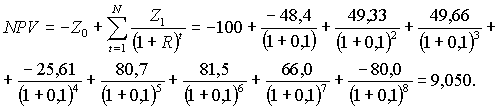
На рис. 43 этот расчет представлен двумя способами. Промежуточные вычисления в колонках E и F соответствуют рекуррентной модели (элементы денежного потока перемножаются на множители приведения).
Готовый результат 109,050 в одной клетке дает табличная формула =NPV(10%;C4:C11), вызывающая специальную финансовую функцию со ссылкой на норму дисконтирования и табличные координаты блока значений элементов денежного потока, расположенных в хронологическом порядке.
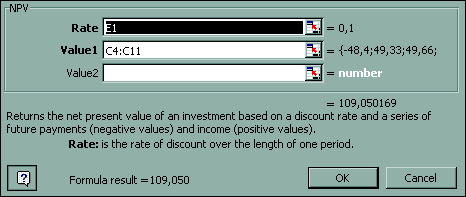
Рис. 43. Диалоговое окно финансовой функции NPV в оригинальной версии Excel.
Необходимо заметить здесь, что, несмотря на название, функция NPV вычисляет не весь чистый, а только дисконтированный доход, то есть Present Value денежного потока (на один период назад от первого поступления/выплаты). Эту особенность табличной функции NPV удобно использовать в расчете индекса рентабельности (англ. profitability index) инвестиционного проекта, относя дисконтированный доход по нему к начальным затратам Z0<0.
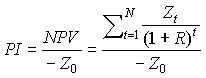 .
. В рассматриваемом примере индекс рентабельности проекта 109%=109,05/100. Это значение можно вычислить по формуле =-NPV(E1;C4:C11)/C3.
Для вычисления чистого дисконтированного дохода к выражению =NPV(10%;C4:C11) необходимо добавить отрицательную величину инвестиционных затрат нулевого периода, записанное в таблице в ячейке C3 (см. формульное выражение в строке ввода над полем рабочего листа на рис.42).
В русифицированной версии Excel (ниже 2000) финансовые функции получили такие идентификаторы, которым далеко не всегда удается поставить в соответствие финансовые термины. Так, например, функция для вычисления дисконтированного дохода в локализованной версии Excel переименована в НПЗ (см. рис. 44).
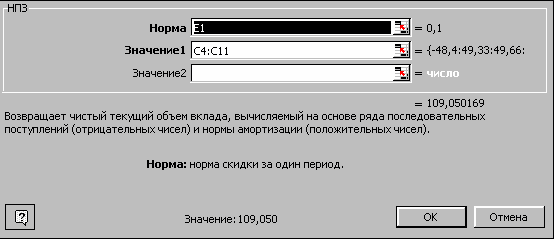
Рис. 44. Диалоговое окно функции NPV=НПЗ.
Несмотря на то что аббревиатура НПЗ в русском языке не расшифровывается ни в какое приемлемое в качестве финансового термина словосочетание, для работы в локализованной версии пользователю придется запомнить именно этот стандартный идентификатор. Читатель, владеющий английским языком, может также самостоятельно убедиться в неадекватности представленного в диалоговом окне перевода смыслу вложенной в эту функцию модели. По-русски более правильно было бы написать, что функция "Возвращает чистый дисконтированный доход инвестиционного проекта, вычисляемый по выбранной норме дисконтирования и потоку будущих выплат (отрицательные значения в денежном потоке) и поступлений (положительные значения). Норма: процентная ставка, принятая в качестве нормы дисконтирования и соответствующая продолжительности единичного периода времени, разделяющего соседние элементы денежного потока инвестиционного проекта". Пояснения справочной системы Excel на русском языке (см. рис. 45) также "не дружат" с финансовой терминологией. В Excel 97 можно добавить к этой справке собственные пояснения, использовав команду Параметры Заметки…
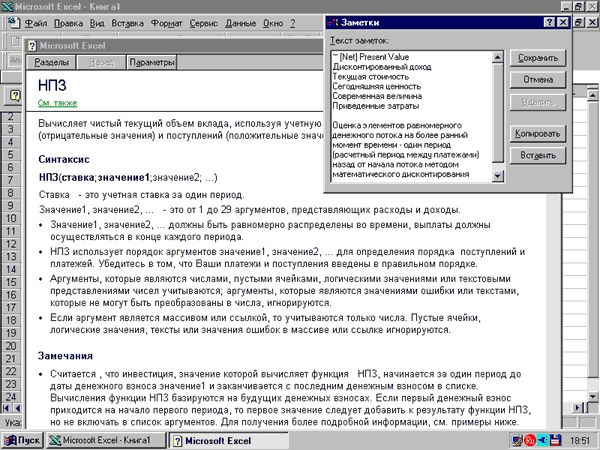
Рис. 45. Дополнение встроенной справочной информации Excel 97
заметками пользователя, уточняющими контекст.
Таблица 13
Сравнение двух проектов, требующих одинаковых вложений капитала
| | Проект 1 | Проект 2 |
| Инвестиции 0 года | -1000 | -1000 |
| Доход 1 года | 200 | 200 |
| Доход 2 года | 300 | 400 |
| Доход 3 года | 600 | 700 |
| Доход 4 года | 500 | 400 |
| Доход 5 года | 100 | 0 |
| Дисконтированный доход по ставке 19% | | |
| Дисконтированный доход по ставке 21% | 980,69 | 1020,23 |
| Дисконтированный доход по ставке 24% | | |
| Чистый дисконтированный доход по ставке 19% | | |
| Чистый дисконтированный доход по ставке 21% | -19,31 | +20,23 |
| Чистый дисконтированный доход по ставке 24% | | |
| Индекс рентабельности при ставке 19% | | |
| Индекс рентабельности при ставке 21% | 98% | 102% |
| Индекс рентабельности при ставке 24% | | |
| Задание Сравните два проекта, денежные потоки которых представлены в табл. 13, при значениях ставки сравнения 19% и 24%. Впишите ответы в свободные клетки табл. 13. Подберите такое значение нормы дисконтирования, при которой чистый дисконтированный доход второго проекта равен нулю. |
| Задание Как оценить срок окупаемости инвестиционного проекта (см. рис. 46)? Какой срок окупаемости короче – простой или дисконтированный? |
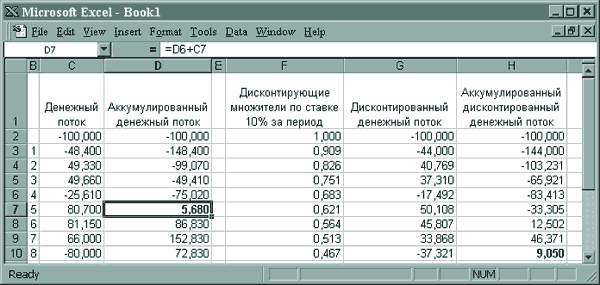
Рис. 46. Определение простого и дисконтированного сроков окупаемости проекта.
Важным критерием принятия инвестиционный решений на основе дисконтирования денежного потока является внутренняя норма доходности (англ internal rate of return). Это такое значение нормы математического дисконтирования, при котором текущая стоимость денежного потока абсолютно равна инвестициям. Внутренняя норма доходности является корнем IRR неявного уравнения, в левой части которого стоит многочлен (полином) степени N.
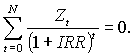
- Из основной теоремы алгебры следует правило знаков Декарта, в соответствии с которым число положительных вещественных корней многочлена, включая кратные, равно k – числу перемен знака в ряду коэффициентов многочлена, или k минус положительно чётное число. Если k = 1, то уравнение имеет единственное положительно решение.
- Следствием правила знаков Декарта является следующее утверждение: если Z0<0 и все Z1,…,ZN 0, то существует единственное решение (1+IRR) > 0, то есть IRR > –1.
- IRR > 0 при условии
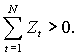
- Справедливо также правило Норстрёма2, сформулированное через число перемен знака в ряду элементов аккумулированного денежного потока (см. рис. 46): если последний член аккумулированного денежного потока не равен нулю, и при этом в ряду значений элементов аккумулированного денежного потока знак меняется только один раз, то для исходного денежного потока существует единственное положительное значение внутренней нормы доходности IRR.
Денежный поток, имеющий единственное положительное значение внутренней нормы доходности IRR, называется регулярным.
Найти значение внутренней нормы доходности в Excel можно подбором параметра (см. рис. 45), или встроенной финансовой функцией IRR = ВНДОХ (см. рис. 46).
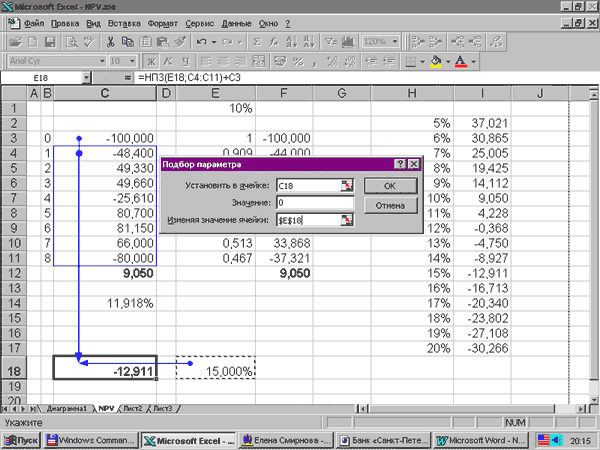
Рис. 45. Подбор значения внутренней нормы доходности.
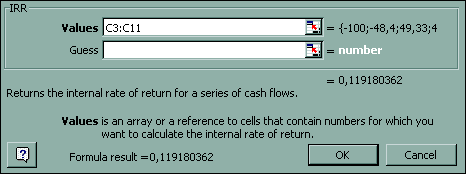
Рис. 48. Вычисление внутренней нормы доходности встроенной функцией IRR = ВНДОХ.
Первый аргумент этой функции – табличный интервал ячеек, где в хронологическом порядке расположены элементы денежного потока, начиная с нулевого. Именно к этому значению программа будет подгонять дисконтированный доход, изменяя процентную ставку. Второй необязательный аргумент (значение 10% установлено по умолчанию) задает предполагаемый ответ для начала итеративной процедуры приближенных вычислений.

1 Коссов В.В., Лившиц В.Н., Шахназаров А.Г. Методические рекомендации по оценке эффективности инвестиционных проектов: официальное издание. М., 1999.
2 Сюдсэтер К., Стрём А., Берк П. Справочник по математике для экономистов. СПб., 2000.
