Блок 1: Рост стоимости вложений за счет присоединения процентов 4

Вид материала

Анализ

Содержание Модуль 2.Эквивалентность финансовых обязательств Эквивалентность финансовых обязательств БЛОК 3: Приведение стоимостных показателей к сопоставимому во времени виду Приведение стоимостных показателей к сопоставимому во времени виду Множитель приведения R – норма дисконтирования; x Процентные ставки называются эквивалентными Средняя ставка простых процентов Таблица 9 Новейшая динамика процентной ставки рефинансирования ЦБ РФ по кредитам3 Период действия Средняя ставка сложных процентов

Подобный материал:

• Возмещение затрат по уплате процентов по кредитам и лизинговых платежей по договорам, 80.46kb.
• Правила определения таможенной стоимости товаров, действующие в рамках вто, 38.09kb.
• Биржевые спекулянты на российском фондовом рынке: в чем различия между новичками, 274.71kb.
• Капитального строительства, 96.76kb.
• В. А. Баумгертнер «Конкурентоспособность российских производителей минеральных удобрений,, 69.53kb.
• Ежедневный мониторинг сми 29 декабря 2011, 202.46kb.
• О реализации приоритетного национального проекта "Развитие апк в северных субъектах, 178.05kb.
• Темы рефератов по дисциплине: «Инвестиции» Принципы и методы оценки стоимости недвижимости, 147.42kb.
• Инструкция Возврат основного долга по кредиту осуществляется на счет №47422810300000000117, 61.51kb.
• Правила определения стоимости активов и величины обязательств, подлежащих исполнению, 58.04kb.

Модуль 2.
Эквивалентность финансовых обязательств

из книги "Техника финансовых вычислений на Excel" ссылка скрыта

Эквивалентность финансовых обязательств

Приведение размера ожидаемой в будущем денежной суммы к эквивалентной ей величине в более ранний момент времени производится умножением на коэффициент приведения.

Приведенная (текущая, настоящая, современная, дисконтированная) стоимость будущего платежа определяется как размер денежной суммы, которую необходимо инвестировать сегодня для того, чтобы в процессе процентного роста в будущем в указанный момент времени она достигла заданной величины.

ссылка скрыта посвящен приведению условий договоров к эквивалентному виду, позволяющему проводить сопоставление финансовых результатов на один и тот же момент времени и уровней доходности за одинаковый период.

ссылка скрыта поможет добросовестному читателю овладеть технологией заполнения электронной таблицы числовой последовательностью с использованием математических законов и моделей роста.

БЛОК 3: Приведение стоимостных показателей к сопоставимому во времени виду

из книги "Техника финансовых вычислений на Excel" ссылка скрыта

Приведение стоимостных показателей к сопоставимому во времени виду

При изучении этого блока вы узнаете, что такое:

• математическое дисконтирование;
  
• эквивалентность условий финансовых контрактов;
  
• средние процентные ставки.
  

Доверяя Банку 1000 руб. на один год по ставке 30% годовых, вкладчик по истечении срока ожидает получить обратно 1300 руб., при этом обеспечивает себе необходимую в будущем сумму, заблаговременно инвестировав поменьше. При положительном темпе прироста дохода (измеряемом процентной ставкой) за выбранный срок, будущая стоимость денежного вклада всегда больше его начальной величины.

Задание Через 270 дней после подписания кредитного договора должник уплатит 1225,00 руб. Кредит выдан под 30% годовых. Какой была исходная сумма долга, если на него только один раз были начислены простые проценты? 1225,00 = 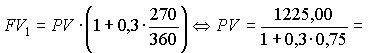Сложные? 1225,00 = 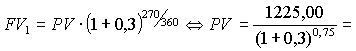Сложные ежемесячно?

Пример. Должник не может выполнить свое обязательство вернуть кредитору в срок 300 000 руб. и предлагает ему удовлетвориться дисконтным векселем Банка номиналом 300 000 руб. со сроком погашения 870 дней, только что приобретенным им по цене 210 000 руб. Кредитор соглашается, и через 9 дней с момента выпуска векселя досрочно предъявляет это долговое обязательство в Банк для погашения. Какую сумму получит кредитор, если при досрочном погашении Банк выплачивает доход по ставке 3% годовых?



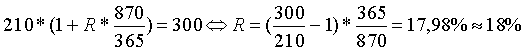
Измерим доходность этого векселя годовой ставкой простых процентов R

В случае досрочного погашения Банк вернет цену векселя и уплатит за использование денежных средств в течение 9 дней по ставке 3%, то есть обязательство вернуть 300 000 руб. через 29 месяцев сегодня оценивается значительно дешевле



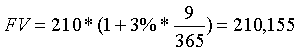
Сравнение размера денежных сумм, разделенных периодом существенной длины, с точки зрения экономической теории процента, корректно только после их приведения к одному и тому же моменту времени. Правило переоценки текущей стоимости будущего платежа на более ранний момент времени, называется математическим дисконтированием. Понятно, что численное значение текущей стоимости зависит от конкретных возможностей вложения средств на заданный срок – от уровня доходности (величины процентной ставки) и способа начисления процентов. Процентная ставка, с учетом которой оценивается текущая стоимость будущего платежа (путем приведения к меньшей сумме в данный момент времени), называется нормой дисконтирования.

Множитель приведения по сложным процентам PVIF(R,N) = 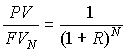, обратный множителю наращения FVIF(R,N) является вторым основным финансовым коэффициентом, обозначаемым аббревиатурой PVIF (от англ. Present Value Interest Factor – процентный множитель текущей стоимости)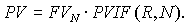





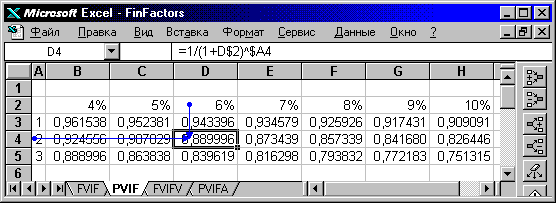
Рис. 19. Построение таблицы множителей приведения PVIF(R,N)
на рабочем листе Excel методом копирования формул.



Рис. 20. Зависимость текущей стоимости 1 000 000 руб.,
ожидаемых через 3 периода, от выбора нормы дисконтирования.

Задание Чему равна текущая стоимость денежной суммы 190 млн руб., ожидаемой через два года при дисконтировании по ставке 6% годовых?

В России в практике принятия инвестиционных решений экономический подход, учитывающий изменение ценности денег во времени, до сих пор соседствует с подходом бухгалтерским, когда общие и средние финансовые показатели за ряд лет исчисляются арифметически без какого-либо дисконтирования. Отчасти это оправдано объективными методическими трудностями при выборе (и особенно прогнозировании!) точного значения нормы сравнения на длительном интервале времени.

Оценка текущей стоимости будущих поступлений и выплат является важным приемом обоснования и принятия решений в инвестиционном анализе. Высокая чувствительность приведенного значения одной и той же будущей суммы к величине процентной ставки, используемой в коэффициенте дисконтирования, заставляет особенно внимательно относиться к выбору методики определения нормы дисконтирования.

Обычно предполагается, что норма дисконтирования должна включать минимально гарантированный уровень доходности доступных инвестору альтернативных вложений капитала, темп инфляции и риск конкретного инвестиционного проекта.

Математически это можно выразить, например, следующей мультипликативной моделью: 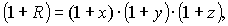где R – норма дисконтирования; x – минимально гарантированная доходность; y – уровень инфляции; z – поправка на риск проекта. Приемлемый уровень риска определяется внутренней структурой капитала¹ инвестора.

Пример². Предприятие планирует возвести на своей территории новое здание, и рассматривает предложения, поступившие от двух строительных фирм, конкурирующих между собой за этот заказ. Сметная стоимость здания одинакова – 190 млн. руб. Срок строительства – два года с момента заключения контракта. До завершения строительства требуется вносить авансовые платежи. На непогашенную этими платежами часть стоимости здания после сдачи его заказчику и начала эксплуатации подрядчики предоставляют возможность отсрочки окончательного расчета под льготный процент.

• Турецкая фирма "Измир" предлагает внести первый аванс размером 40 млн руб. через год с момента подписания контракта, и второй аванс – 50 млн руб. – через два года, в момент окончания строительства. На оставшуюся сумму 100 млн руб. (исчислена бухгалтером арифметически) предоставляется отсрочка платежа на 1 год по ставке 7% годовых.
  
• Фирма "Иматра" из Финляндии просит внести три авансовых платежа: первый платеж 10 млн руб. сейчас, и еще два одинаковых по 40 млн руб. дважды – через год и в момент сдачи здания заказчику. На оставшуюся часть стоимости здания дается годовая отсрочка под 4% годовых.
  

Какую сумму достаточно сегодня инвестировать по ставке доходности 10% годовых, чтобы по мере необходимости рассчитываться с подрядчиком в соответствии с условиями контракта? Ответ на этот вопрос дает возможность сравнить предложения на момент принятия решения о выборе подрядчика.





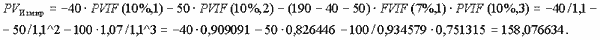
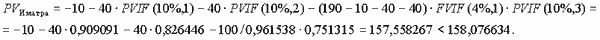
Второе предложение более выгодно фирме-заказчику по критерию минимума суммы затрат, приведенных к начальному моменту времени.



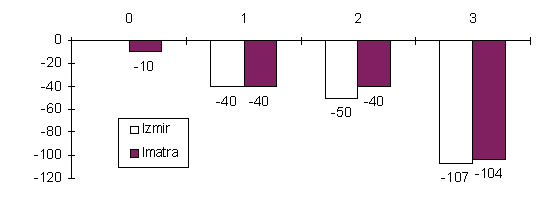
Рис. 21. Распределение затрат на строительство во времени.

Приведение вариантов к сопоставимому виду необязательно ориентировать на более ранний момент времени, можно их сравнивать, например, по критерию будущей стоимости, которую можно нарастить на банковском счете под заданный процент, за счет отказа от расходов по контракту. В общем случае платежи можно сравнивать применительно к любому моменту времени внутри срока данного финансового обязательства. Давайте оценим текущую стоимость контракта "Иматра" на момент окончания строительства (год 2) по ставке сравнения 10% годовых.



Проверка



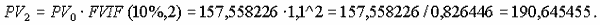
Текущая стоимость 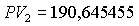эквивалентна 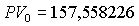, относящейся к моменту времени "два периода назад" при сравнении по норме доходности 10% сложных за один процентный период.

Задание Предположим, что фирма "Измир" до подписания контракта узнала о том, что предложение ее конкурента с точки зрения заказчика более приемлемо, и решила снизить процент за отсрочку последнего платежа с 7% до 5%. Найдите текущую стоимость платежей предприятия этому подрядчику при новых условиях контракта. Сравните также контракты "Иматра" и "Измир 5%" на момент полного погашения долга (год 3) при дисконтировании по ставке 9% годовых. Необходимые для расчетов значения множителей приведения PVIF(9%,N), обратные множителям будущей стоимости FVIF(9%,N), можно найти в рабочей таблице на рис. 19.

• Финансовые операции считаются эквивалентными, если суммы дохода по ним, приведенные к одному и тому же моменту времени, совпадают.
  
• Финансовые операции считаются эквивалентными по уровню доходности, если их эффективные ставки (или будущие стоимости единичной инвестиции по прошествии года) совпадают.
  
• Процентные ставки называются эквивалентными, если при замене в контракте одной из них на другую за тот же срок финансовые результаты не изменятся.
  

Эквивалентные друг другу значения сравниваемых между собой процентных ставок обычно выводятся из уравнения эквивалентности – условия равенства множителей наращения за одно и то же время начисления процентов.

Пример. Найдем, годовую ставку обыкновенных сложных процентов с ежедневным начислением, эквивалентную годовой доходности 30,8%. Искомую номинальную величину ставки R можно выразить явно из соотношения



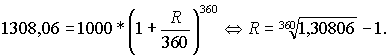
В случае возникновения технических проблем с извлечением корня 360 степени можно решить это уравнение итеративно - подбором искомого значения R методом проб и ошибок.

Для нахождения процентных ставок, эквивалентных на заданном интервале времени переменным ставкам, применяются средние процентные ставки, метод вычисления которых зависит от выбранного правила начисления процентов. Формула среднего выводится из уравнения эквивалентности.

Задание Какой силе роста при непрерывном начислении процентов эквивалентна годовая доходность 30,8%? 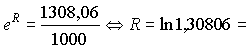Какая годовая ставка простых процентов эквивалентна ставке 60% сложных годовых при их ежеквартальном начислении в течение полутора лет? В течение одного года (см. рис. 22)?

Средняя ставка простых процентов определяется из условия равенства множителей наращения за полный срок N, равный сумме более мелких интервалов времени 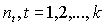, на которых переменная процентная ставка сохранялась постоянной на уровнях 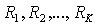соответственно.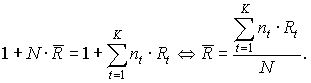





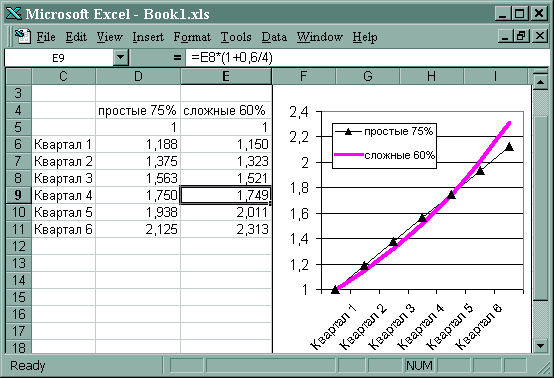
Рис. 22. Равенство множителей наращения по эквивалентным ставкам за 1 год = 4 квартала.

Пример. По вкладам до востребования в рублях с начала 1999 г. действовала ставка 3%, с 1 декабря 1999 г. она была снижена до 2%, а с 21 марта 2000 г. до 1% годовых.

Найдем среднюю ставку простых процентов за период с 01/05/1999 по 01/05/2000 (два варианта организации вычислений в таблице см. на рис. 23).



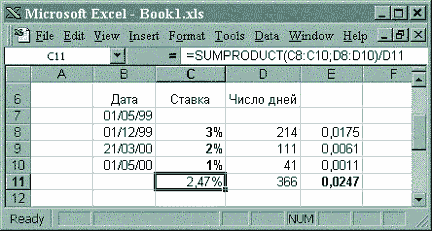
Рис. 23. Средняя процентная ставка, взвешенная по периодам действия.

Средняя ставка простых процентов есть арифметическая средняя с весами, равными длительности отдельных периодов.

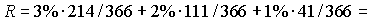
Задание Используя данные табл. 9, найдите среднее значение учетной ставки ЦБ РФ с 01/04/99 по 01/04/00.

Таблица 9
Новейшая динамика процентной ставки рефинансирования ЦБ РФ по кредитам³

Период действия	% годовых
24/07/98 – 09/06/99	60%
10/06/99 – 23/01/00	55%
24/01/00 – 06/03/00	45%
07/03/00 – 20 03/00	38%
21/03/00 – 09/07/00	33%
10/07/00 – 03/11/00	28%
04/11/00	25%

Средняя ставка сложных процентов является корнем уравнения, поэтому множитель будущей стоимости по средней ставке сложных процентов находится по формуле взвешенной средней геометрической.

.

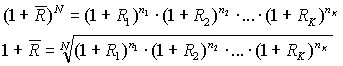Пример. Среднемесячный темп инфляции за 10 месяцев 2000 г.

Используя приведенные на рис. 24 данные Госкомстата РФ⁴ об изменении индекса потребительских цен, оценим показатель инфляции за месяц, то есть найдем такой среднемесячный темп роста индекса потребительских цен h, что



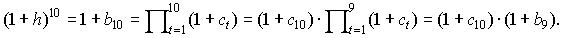
где t – порядковый номер месяца в 2000 г., t = 1, … ,10;

b_t – базисный индекс цен в месяце t по сравнению с декабрем 1999 г. (t = 0);

c_t – цепной индекс цен в месяце t по сравнению с предыдущим месяцем t – 1.



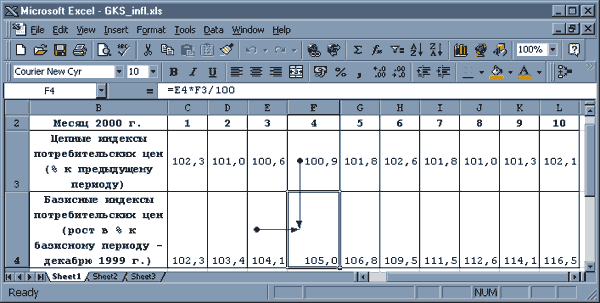
Рис. 24. Динамика показателя инфляции за 10 месяцев 2000 г.

Здесь показан вариант организации рекуррентного табличного вычисления базисного за период t индекса b_t как произведения цепного индекса данного периода с_е на базисный индекс предпоследнего периода b_t-1 с учетом того, что b₁ = c₁. В результате получено значение b₁₀ = 116,5%. Cреднемесячный индекс потребительских цен (1 + h) находим по формуле среднего геометрического, приняв длину каждого месяца за постоянную величину (1 месяц = 30 дней). При этом предположении в формуле средневзвешенного среднего геометрического все весовые показатели n_t = 1, а их сумма N = 10. Тогда



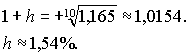
Для переоценки с учетом инфляции стоимости основных фондов и имущества в момент реализации используется дефлятор ИРИП (Индекс стоимости Реализуемого Имущества Предприятия)⁵. На рис. 25. показано поквартальное увеличение реальной стоимости имущества, приобретенного в начале 1998 г. по цене 80 млн. руб., к моменту реализации в начале 2001 г. (без учета амортизации).



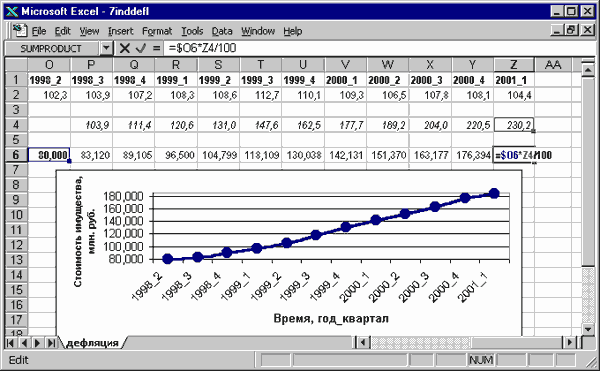
Рис. 25. Рост реальной стоимости имущества с учетом инфляции.




1 См.: Бригхем Ю., Гапенски Л. Финансовый менеджмент / Пер.с англ. СПб., 1998.
2 Пример является переработанной задачей из кн.: Бухвалов А.В., Идельсон А.В. Самоучитель по финансовым расчетам. М., 1997.
3 Источник: «АКДИ Экономика и жизнь» – ссылка скрыта
4 Источник: «АКДИ Экономика и жизнь» – ссылка скрыта
5 Источник: «АКДИ Экономика и жизнь» – ссылка скрыта