Заглушённая камера
| Вид материала | Документы |
- nyj narod, 2028.78kb.
- Исходные технические данные, 34.3kb.
- 125009 Москва, ул. Тверская, 471.48kb.
- Камера джон гришем перевод с английского Ю. Кирьяка. Ocr tymond Анонс, 6452.48kb.
- Конспект урока по теме: «Симметрия математический закон красоты», 47.79kb.
- Инт камера в следственном изоляторе, 455.72kb.
- Технические характеристики: камера должна обеспечивать загрузку и работу с пластинами, 503.09kb.
- В спбгу готовят футбольную команду роботов, 409.13kb.
- Ракетный корабль "галилей" Роберт хайнлайн, 2081.67kb.
- Ксавьера Холландер, 2629.75kb.
| ЗЕМНОЙ МАГНЕТИЗМ (геомагнетизм), 1) магнитное поле Земли. 2) Раздел геофизики, изучающий распределение в пр-ве и изменения во времени магн. поля Земли, а также связанные с ним физ. процессы в Земле и в атмосфере. В каждой точке пр-ва геомагн. поле характеризуется вектором напряжённости Т, величина и направление к-рого определяются тремя составляющими X, Y, Z (северной, восточной и вертикальной) в прямоуг. системе координат (рис.) или тремя элементами З. м.: горизонтальной составляющей напряжённости Н, магн. склонением D (угол между Н и плоскостью геогр. меридиана) и магн. наклонением I (угол между Т и плоскостью горизонта). Существование у Земли магн. поля (т. н. основного, или постоянного, поля, его вклад ~99%) объясняют процессами, протекающими в жидком металлическом ядре Земли (см. Динамо-эффект). Осн. поле до высот ~3Rзем (Rзем— радиус Земли) имеет дипольный хар-р, но на больших высотах структура ноля значительно сложнее (см. Магнитосфера). Магн. полюсы Земли (точки, где Н= 0) не совпадают с её геогр. полюсами — дипольный магн. момент Земли, равный 8•1025 ед. СГС, образует с осью вращения Земли угол 11,5°. Напряжённость геомагн. поля Т убывает от магн. 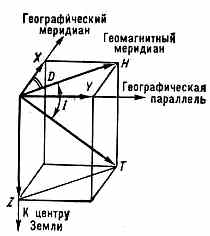 Составляющие магнитного поля Земли. полюсов к магн. экватору (линии, где /=0) от 55,7 до 33,4 А/м (от 0,70 до 0,42 Э). Осн. магн. поле испытывает лишь медленные вековые изменения (вариации). В разные геол. эпохи геомагн. поле имело разл. полярность, т. е. с периодом от сотен тыс. лет до десятков млн. лет происходит переполюсовка осн. магн. поля Земли. Переменное геомагн. поле (~1%), порождаемое токами в магнитосфере и ионосфере, более неустойчиво. Наблюдаются периодич. солнечно-суточные и лунно-суточные магн. вариации соответственно с амплитудами 30—70 и 1 — 5 (1=10-5 Э). Обтекание магнитосферы плазмой солнечного ветра с переменными плотностью и скоростью заряж. ч-ц, а также прорывы ч-ц в магнитосферу приводят к изменению токовых систем в магнитосфере и ионосфере. Токовые системы в свою очередь вызывают в околоземном косм. пр-ве и на поверхности Земли колебания геомагн. поля в широком диапазоне частот (от 10-5 до 102 Гц) и амплитуд (от 10-3 до 10-7 Э). Сильные возмущения магнитосферы — магн. бури — сопровождаются появлением в верх. атмосфере Земли полярных сияний, ионосферных возмущений, рентг. и НЧ излучений. • Яновский Б. М., Земной магнетизм, 4 изд., Л., 1978; С т е й с и Ф. Д., Физика Земли, пер. с англ., М., 1972. ЗЕРКАЛО АКУСТИЧЕСКОЕ, гладкая поверхность, линейные размеры к-рой велики по сравнению с длиной волны падающего звука, формирующая регулярное отражение звук. волн. Поверхность считается гладкой, если шероховатости её меньше /20. Св-ва акустич. З. характеризуются коэфф. отражения, к-рый определяет энергию отражённой волны, и формой его поверхности, к-рая обусловливает вид отражённой волны. З. а. применяются для изменения направления распространения и фокусировки звука. Напр., плоское З. а. изменяет лишь направление распространения волны, а коническое изменяет не только направление распространения, но и вид отражённой волны. Параболоидное З. а. изменяет направление и вид плоской волны, превращая её в сходящуюся сферич. волну, а эллипсоидное изменяет только направление распространения волны, преобразовывая расходящуюся сферич. волну в сходящуюся в др. фокусе сферич. волну. • Каневский И. Н., Фокусирование звуковых и ультразвуковых волн, М., 1977. И. Н. Каневский. ЗЕРКАЛО ОПТИЧЕСКОЕ, тело, обладающее полированной поверхностью правильной формы, способной отражать световые лучи с соблюдением равенства углов падения и отражения, и образующее изображения оптические предметов (в т. ч. источников света), положение к-рых может быть определено по законам геометрической оптики. Наиболее распространены плоские З. о. В оптических системах применяются также выпуклые и вогнутые З. о. со сферич., параболоидальными, эллипсоидальными, тороидальными и др. отражающими поверхностями. Кач-во З. о. тем выше, чем ближе форма его поверхности к математически правильной. Микронеровности отражающих поверхностей З. о. должны быть малы по сравнению с длиной световой волны (см. Отражение света). Максимально допустимая величина микронеровностей поверхностей определяется назначением З. о. Так, для астр. приборов она не должна превышать 0,1 наименьшей длины волны падающего на З. о. излучения, в то время как для прожекторных или конденсорных З. о., отражающих большие световые потоки, она может быть в 10—100 раз больше. Неплоские З. о. обладают всеми присущими оптич. системам аберрациями, кроме хроматических (см. Аберрации оптических систем). Плоское З. о.— единственная оптич. система, к-рая даёт полностью безаберрац. изображение (всегда мнимое) при любых падающих на него пучках света. 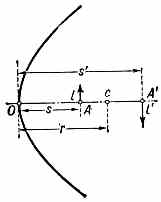 Рис. 1. Схема зеркала с параболоидальной поверхностью; l — предмет; l' — изображение предмета. Положения предмета и его изображения, даваемого З. о. со сферич., параболоидальной или др. поверхностью, имеющей ось симметрии, связаны с радиусом кривизны r З. о, в его вершине О (рис. 1) соотношением: l/s+l/s' = 2/r, где s — расстояние от вершины З. о. до предмета А, s' — рас- 200 стояние до изображения А'. Эта ф-ла строго справедлива лишь в предельном случае бесконечно малых углов, образуемых лучами света с осью З. о.; однако она явл. хорошим приближением и при конечных, но достаточно малых углах. Если предмет находится на бесконечно большом расстоянии, то s' равно фокусному расстоянию З. о.: s'=f'=r/2. Фокальная плоскость (см. Фокус) расположена на расстоянии r/2 от вершины З. о. 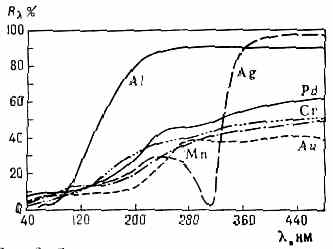 Рис. 2. Спектральные коэфф. отражения металлич. плёнок. З. о. должно иметь высокий отражения коэффициент. Большими коэфф. отражения обладают металлич. поверхности: алюминиевые — в УФ, видимом и ИК диапазонах, серебряные — в видимом и ИК, золотые — в ИК. Отражение от любого металла сильно зависит от длины волны К света: с её увеличением коэфф. отражения возрастает для нек-рых металлов до 99% (рис. 2). Коэфф. отражения у диэлектриков значительно меньше, чем у металлов (стекло с показателем преломления n=1,5 отражает всего 4%). Однако, используя интерференцию света в многослойных комбинациях прозрачных диэлектриков, можно получить отражающие (в относительно узкой области спектра) поверхности с коэфф. отражения более 99% не только в видимом диапазоне, но и в УФ, что невозможно получить от З. о. с металлич. поверхностями. Диэлектрич. З. о. состоят из большого числа (13—17) слоев диэлектриков попеременно с высоким и низким п. Оптическая толщина каждого слоя составляет /4 (см. Оптика тонких слоев). Нечётные слои делаются из материала с высоким n (напр., из сульфидов цинка, сурьмы, окислов титана, циркония, гафния, тория), а чётные — из материала с низким n (фторидов магния, стронция, двуокиси кремния). Коэфф. отражения диэлектрич. З. о. зависит не только от , но и от угла падения излучения. Наиболее распространённый способ изготовления З. о.— нанесение отражающих металлич. или диэлектрич. покрытий на полированную стеклянную поверхность катодным распылением или испарением в вакууме. З. о., применяемые самостоятельно и в сочетании с линзами, образуют обширную группу зеркальных и зеркально-линзовых приборов. Безаберрационность плоских З. о. позволила широко использовать их для поворота светового пучка, автоколлимации, переворачивания изображений и т. д. Плоские З. о. используются также в зеркальной развёртке оптической и скоростной киносъёмке; З. о. входят в состав точнейших измерит. приборов, напр. интерферометров. С созданием лазеров З.о. стали применяться в кач-ве отражающих плоскостей, оптических резонаторов. Отсутствие хроматин, аберраций в З. о. обусловило использование их в телескопах, монохроматорах (особенно ИК излучения) и во многих др. приборах. • Тудоровский А. И., Теория оптических приборов, 2 изд., ч. 2, М.— Л. 1952; Слюсарев Г. Г., Методы расчета оптических систем, 2 изд., Л., 1969. В. Н. Рождественский. ЗЕРКАЛЬНОЕ ОТРАЖЕНИЕ света, см. в ст. Отражение света ЗЕРКАЛЬНОЙ СИММЕТРИИ ПРАВИЛО, то же, что Лёвшина правило. ЗЕРКАЛЬНО-ЛИНЗОВЫЕ СИСТЕМЫ (катадиоптрические системы), оптич. системы, содержащие отражающие (зеркала оптические) и преломляющие поверхности (линзы). В нек-рых З.-л. с. зеркала выполняют чисто конструктивные функции (изменение направления светового пучка, уменьшение габаритов прибора и т. п.), не 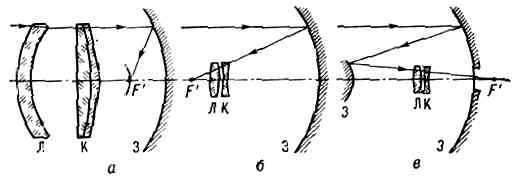 Оптич.схемы зеркально-линзовых систем с линзовыми компенсаторами ЛК аберраций: а — сверхсветосильный объектив с большим углом зрения (до 30°) для фотосъемки движущихся небесных тел; б — телескоп с параболоидальным зеркалом, в — система с параболоидальным большим зеркалом и сферическим малым зеркалом З. влияя на кач-во изображения. Примером таких систем могут служить зеркально-линзовые конденсоры микроскопов. В других случаях зеркала играют осн. роль в образовании изображений, а линзы служат гл. обр. для исправления аберраций, вносимых зеркалами (см. Аберрации оптических систем). Оптич. св-ва зеркал не меняются при изменении длины волны падающего света (т. е. зеркала ахроматичны), поэтому З.-л. с. широко применяются в случаях, когда оптич. система должна обладать большим фокусным расстоянием и большим диаметром (напр., объективы телескопов). Одна из осн. областей применения З.-л. с.— астрономия. Сочетание зеркал разной формы и разл. комбинаций линзовых компенсаторов позволило создать З.-л. с. с большим углом зрения и светосилой (рис., а, б), уменьшить длину астр. и фотогр. приборов (рис., в). З.-л. с. используются в кач-ве светосильных фотогр. объективов и телеобъективов. У этих систем сравнительно небольшое поле зрения, однако их разрешающая способность выше, чем у линзовых объективов с такими же хар-ками. З.-л. с. применяются при конструировании объективов микроскопов. Такие объективы обычно взаимозаменяемы с линзовыми, но обладают рядом преимуществ, особенно при исследовании в УФ лучах. В микроскопах также широко используется осветительная З.-л. с.— конденсор. Ахроматичность и высокий коэфф отражения зеркал в широкой спектр области обусловили использование З.-л. с. и в др. приборах, работающих в УФ и ИК областях спектра (в частности, в спектральных приборах). • См. лит. при ст. Зеркало оптическое, Линза. Г. Г. Слюсарев. ЗЕРКАЛЬНЫЕ АНТЕННЫ, антенны, в к-рых формирование диаграммы направленности осуществляется с помощью отражающих поверхностей — зеркал. Их появление восходит к классическим экспериментам нем. физика Г. Герца, применившего в 1888 в кач-ве фокусирующего зеркала параболич. цилиндр. З. а. состоит из одного или неск. облучателей и одного зеркала или системы зеркал. Используются параболич., эллиптич., гиперболич., сферич., плоские зеркала и их комбинации, а также параболич цилиндр, сегментно-параболич. цилиндр параболич. тор и т. п. (рис. 1). Наиболее распространены однозеркальные антенны, облучаемые из фокуса / или из фокальной линии. В простейших многозеркальных антеннах используется параболич. зеркало и конфокальный с ним гиперболоид или эллипсоид, другой фокус к-рого расположен на поверхности гл. параболич. зеркала (рис. 2). К З. а относятся также перископические антенны (рис. 3, а) и антенны переменного профиля Хайкина — Кайдановского (рис. 3, б). К З. а. относятся также рупорно-параболические антенны и антенны типа раковины. З. а. широкодиапазонны, позволяют формировать различные (в т. ч. весьма узкие) диаграммы направленности и осуществлять как механич , так и электрич. сканирование. Они обладают большим усилением и малыми потерями, их шумовая темп-ра 201 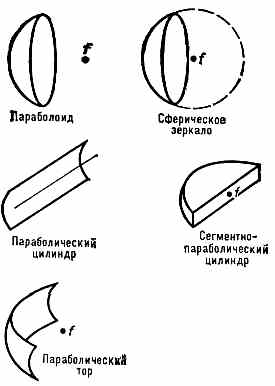 Рис. 1. Элементы зеркальных антенн. 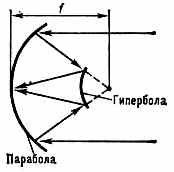 Рис. 2. Двухзеркальные антенны: вверху — антенна Кассегрена; внизу — антенна Грегори. 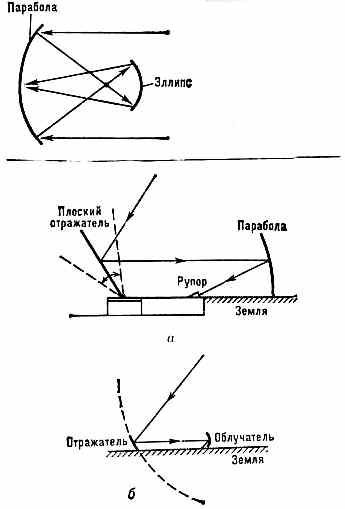 Рис. З. а — перископич. антенна; б — антенна перем. профиля. может быть очень низкой. Всё это обусловило их широкое использование в радиоастрономии, косм. радиосвязи и радиолокации и т. д. • См. лит. при ст. Антенна. Н. М. Цейтлин. ЗЕРКАЛЬНЫЕ ЯДРА, два атомных ядра, отличающихся тем, что при одинаковом числе нуклонов число нейтронов в одном из них равно числу протонов во втором. Примеры З. я.: 31Н—32Не,73Li—74Be, 146С—148О. З. я. являются членами одного изоспинового мультиплета. Вследствие изотопической инвариантности яд. сил (независимости яд. сил от заряда взаимодействующих нуклонов) массы З. я. отличаются друг от друга только за счёт кулоновской энергии отталкивания протонов и разности масс нейтрона и протона. Это соотношение выполняется с хорошей точностью (порядка 0,1%). ЗИВЕРТ (Зв), в СИ наименование единицы эквивалентной дозы излучения, рекомендованное 16-й Генеральной конференцией по мерам и весам (1979). 1Зв=1 Дж/кг=102 бэр. ЗОНА МОЛЧАНИЯ в акустике (зона акустической тени), область, в к-рой звук от удалённых мощных источников (орудийная стрельба, взрыв и т. д.) не слышен, в то время как на больших расстояниях от источника он снова появляется (т. н. зона аномальной слышимости). З. м. обычно имеют на земной поверхности форму неправильного кольца, окружающего источник звука. Иногда наблюдаются две и даже три З. м., разделённые зонами аномальной слышимости. Внутр. радиус 1-й З. м. обычно равен 20— 80 км, иногда он достигает 150 км; внеш. радиус может достигать 150— 400 км. Причиной образования З. м. явл. рефракция звука в атмосфере. Аналогичное явление наблюдается часто и при распространении звука (УЗ) в океане (см. Гидроакустика). • X р г и а н А. X., Физика атмосферы, 2 изд., т. 1—2, Л., 1978; Толстой И., К л е й К. С., Акустика океана, М., 1969, гл. 5. ЗОНД АКУСТИЧЕСКИЙ, устройство для измерения звукового давления в заданной точке звук. поля, обеспечивающее мин. искажения поля, вызванные самим процессом измерения. З. а. представляет собой тонкую трубку А (рис.) или тв. стержень, изолированный от окружающей среды, один конец к-рого вводится в исследуемую область звук. поля, а второй соединяется с приёмником звука D.  Для исключения резонансных явлений и осуществления режима бегущей волны за приёмником к трубке (стержню) присоединяется длинный звукопровод В, обладающий значит. поглощением. З. а. применяются для измерений в малых объёмах и труднодоступных местах. • Беранек Л., Акустические измерения, пер. с англ., М., 1952; Блинова Л. П., Колесников А. Е., Ланганс Л. Б., Акустические измерения, М., 1971. И. П. Голямина. ЗОННАЯ ПЛАСТИНКА Френеля (пластинка Сорэ), в простейшем случае стеклянная пластинка, состоящая из системы чередующихся прозрачных и непрозрачных концентрич. колец, построенных по принципу расположения ион Френеля. З. п. явл. по существу дифракционной решёткой. З. п. (рис.) 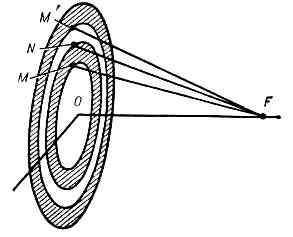 делит падающую на неё волну на кольцевые зоны, ширина к-рых подобрана так, чтобы расстояние от краёв зоны до точки наблюдения F, наз. фокусом З. п., изменялось на половину длины волны : NF-MF=/2, при этом фазы волн, приходящих в F из соответствующих точек N и М соседних зон, противоположны. Если между точечным источником света и точкой наблюдения расположить З. п. с к прозрачными кольцами, соответствующими нечётным зонам Френеля (чётные зоны — непрозрачные), то действие всех выделенных (прозрачных) зон сложится и амплитуда колебаний в точке наблюдения возрастёт в 2k раз; то же произойдёт, если прозрачными будут чётные зоны, но фаза суммарной волны будет иметь противоположный знак. Если на стеклянную пластинку вместо непрозрачного слоя нанести прозрачный слой, вызывающий сдвиг фазы на /2, то интенсивность света в точке наблюдения возрастёт в 4k раз. Примером З. п. может служить голограмма точечного источника; особенностью голограммы как З. п. явл. то, что переход от тёмного поля к светлому осуществляется не скачком, а плавно, прибл. по синусоидальному закону. Для оптич. излучения с длиной волны З. п. действует как положительная линза, но хроматическая аберрация такой системы приблизительно в 20 раз больше, чем у линз из стекла типа «крон». Аналогичные устройства могут быть созданы и в диапазоне радиоволн, где благодаря значительно большим длинам волн реализация описанного принципа упрощается и оказывается возможным создание направленных излучателей типа зонных антенн. Л. Н. Капорский. 202 ЗОННАЯ ТЕОРИЯ твёрдых тел, квантовая теория энергетич. спектра эл-нов в кристалле, согласно к-рой этот спектр состоит из чередующихся зон (полос) разрешённых и запрещённых энергий. З. т. объясняет ряд св-в и явлений в кристалле, в частности разл. хар-р электропроводности тв. тел. Основы З. т. созданы нем. физиком Ф. Блохом (1928) и франц. физиком Л. Бриллюэном (1930). В основе З. т. лежит т. н. о д н о э л е к т р о н н о е п р и б л и ж е н и е, базирующееся на след. упрощениях: 1) ат. ядра в узлах идеальной крист. решётки неподвижны (их масса велика по сравнению с массой эл-нов). 2) Эл-н движется в поле периодич. потенциала U(r) (r — пространств. координата точки), к-рое складывается из полей, создаваемых ядрами и остальными эл-нами. 3) Это периодич. поле обладает трансляц. инвариантностью: U(r+an)=U(r), (1) где аn — вектор n-го узла решетки. В такой модели для волн. ф-ции эл-на в решётке выполняется теорема Блоха: k(r)=uk(r)exkr, (2) где uk(r+a)=uk(r), k — волновой вектор эл-на. Это означает, что k(r) имеет вид волн. ф-ции свободного эл-на, амплитуда к-рой промодулирована в пр-ве с периодом решётки. Спектр энергии 8 эл-нов можно определить, подставляя волн. ф-цию в виде (2) в стационарное Шредингера уравнение и вводя те или иные граничные условия. Решение ур-ния даёт энергетич. спектр в виде серии полос разрешённых энергий ξl(k) (l — номера разрешённых зон), разделённых полосами запрещённых энергий. Из (1) следует, что ξl(k+b)=ξl(k), где b — вектор обратной решётки. Следовательно, ξl(k) — периодич. ф-ция с периодом b. Физически разл. значения k заключены внутри первой Бриллюэна зоны. В соответствии с З. т. движение эл-на в решётке сходно с движением эл-на в свободном пр-ве, однако фактически носит туннельный хар-р. Квазиимпульс эл-на в ре-щётке p=hk отличен от импульса свободного эл-на. Для него выполняются законы сохранения, справедливо ур-ние движения dp!dt=F (F — внеш. сила). Эл-н в кристалле оказывается квазичастицей с эффективной массой m*, отличной от массы свободного эл-на m0. Энергия эл-на явл. ф-цией квазиимпульса ξ(р). Энергетич. структура каждой зоны описывается ф-цией ξ(р), наз. дисперсии законом. Есть два осн. способа описывать энергетич. структуру зоны: 1) пусть координаты рх, ру и рz фиксированы, тогда ξ(рx) — кривая на плоскости (ξ, рх) (дисперсионная кривая, рис. 1). Повторяя эту операцию для (ξру) и (ξрг) получим набор дисперс. кривых, полностью характеризующих ф-цию ξ(p). 2) Можно фиксировать какое-то значение энергии в к.-л. зоне ξl(p)=const. Это ур-ние поверхности в трёхмерном р-пространстве (изоэнергетич. поверхность). Изменяя константу, получим семейство изоэнергетич. поверхностей, характеризующих закон дисперсии. Изоэнергетич. поверхности обладают симметрией, связанной с симметрией кристаллов. Физически происхождение зонной структуры энергетич. спектра эл-нов в кристалле связано с образованием 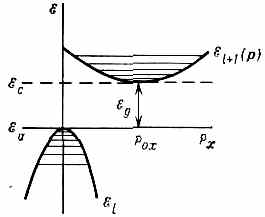 Рис. 1. Дисперсионные кривые ξl(рх) и ξl-1(px) при фиксированных pу и pz: ξс — дно l+1-й зоны (зоны проводимости), ξv — потолок l-той зоны (валентной зоны); ξg — ширина запрещённой зоны; заштрихованные области — уровни, заполненные эл-нами и дырками. кристалла из N атомов, каждый из к-рых в свободном состоянии обладает дискретным электронным энергетич. спектром. При объединении N атомов в кристалл последний можно трактовать как гигантскую молекулу, в к-рой эл-ны всех атомов обобществлены и к-рую следует рассматривать как единую квантовомеханич. систему. В кристалле каждый из ат. уровней превращается в полосу, состоящую из N уровней (или с учётом спина — из 2N уровней), к-рая явл. разрешённой зоной ξl(p). Если на атом приходится Z эл-нов, то полное число эл-нов в кристалле равно NZ; они занимают уровни разрешённых зон начиная снизу, пока не будут полностью исчерпаны. Изоэнергетич. поверхность, соответствующая Ферми энергии: ξ(p)=ξF, наз. Ферми поверхностью. Ниж. зоны (довольно узкие) будут целиком заполнены эл-нами внутр. оболочек атомов. Заполнение эл-нами разрешённых энергетич. уровней происходит в соответствии с Ферми — Дирака распределением. Хотя структура энергетич. зоны дискретна, уровни весьма близки (квазинепрерывны). Для описания распределения энергетич. уровней в зоне n(ξ) часто вводят ф-цию плотности состояний (уровней) g(ξ)=dn/dξ — число уровней на единичный энергетич. интервал. Вид ф-ции g(ξ) зависит от закона дисперсии. В простейшем случае, когда ξ(р)=р2/2m*, то g(ξ)=Aξ1/2, где А=(1/42) (2m*/h2)3/2. Физ. св-ва кристаллов определяются в осн. верхними зонами, ещё содержащими эл-ны. Эиергетич. интервал ξg между «дном» ξc (минимумом энергии) самой верхней ещё содержащей эл-ны зоны и «потолком» ξv (максимумом энергии) предыдущей целиком заполненной зоны, наз. запрещённой зоной (хотя ниже по энергии может быть ещё неск. др. запрещённых и разрешённых зон). Если при T=0 все зоны, содержащие эл-ны, заполнены эл-нами целиком, а следующая «пустая» разрешённая зона отделена от данной достаточно широкой запрещённой зоной, то кристалл явл. диэлектриком (напр., у алмаза ξg~5 эВ); если ξg3 эВ, то — полупроводником. Если верхняя содержащая эл-ны зона заполнена эл-нами частично, то это металл. Возможно частичное перекрытие разрешённых зон или смыкание их (полуметаллы, бесщелевые полупроводники). Внеш. воздействия (повышение темп-ры, облучение, напр. светом, или сильные внеш. электрич. поля) могут вызвать переброс эл-нов через запрещённую зону. В результате появляются «свободные» носители заряда (эл-ны проводимости и дырки), осуществляющие проводимость. В ПП изоэнергетич. поверхность в зоне проводимости в простейшем случае явл. сферой или эллипсоидом. В более сложных случаях изоэнергетич. поверхность может быть многосвязной, напр. в виде совокупности эллипсоидов, «нанизанных» своими длинными осями на оси симметрии изоэнергетич. поверхности (рис. 2); для Ge их 8, для Si — 6. В этом случае в зоне проводимости есть неск. эквивалентных минимумов энергии. Области энергии в зоне проводимости вблизи каждого из минимумов наз. долинами, а ПП с неск. эквивалентными минимумами — многодолинными. В условиях равновесия эл-ны распределяются между долинами поровну. 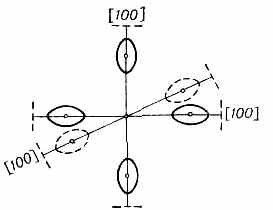 Рис. 2. Эллипсоиды пост. энергии в Si. При включении в данном направлении внеш. электрич. поля долины проявляют себя неэквивалентно из-за различий в величине эфф. масс и подвижностей эл-нов в разл. направлениях. Аналогичные эффекты имеют место и при воздействии одностороннего давления. Следствием 203 этой неэквивалентности может быть, в частности, анизотропия электропроводности, оптич. св-в и т. п. Локальные нарушения идеальности решётки (примесные атомы, вакансии и др. дефекты) могут вызвать образование разрешённых локальных уровней и локальных зон внутри запрещённых зон. Применение З. т. возможно и в этом случае, и даже в случае аморфных тв. тел, хотя требует нек-рых модификаций (см. Неупорядоченные системы). • См. лит. при ст. Твёрдое тело. А. А. Гусев, Э. М. Эпттейн. |
