С 2007 Группа 04-102, 2 семестр
| Вид материала | Закон |
- Лекций студентами Кафедра биологии дисциплина ботаника группа, 75.84kb.
- Темы рефератов по дисциплине: «Оcновы аудита» Сущность аудиторской деятельности, 153.15kb.
- Курс, группа у-5360, срок обучения 4 года 4 месяца, осенний семестр 2007-2008 учебного, 158.22kb.
- Список публикаций педагогов моу сош №102 в 2007-2008 учебном году, 38.48kb.
- Году в Республике Коми составил 103,0% к уровню 2007 года, что выше среднероссийского, 240.16kb.
- График контрольных мероприятий по учебным дисциплинам III курс I семестр группа 3394,3395, 94.19kb.
- Анализ ситуации на рынке производства сахара, 81.6kb.
- Сп 41-102-98, 1743.38kb.
- Никитина Ирина Александровна, д э. н., профессор, sizn@mail ru Бакалаврская программа, 154.15kb.
- Курс 5 Семестр: 9-10 Астана 2011 7 Сведения о преподавателях, 325.38kb.
11. Вихревой характер магнитного поля. Теорема о циркуляции вектора индукции магнитного поля в интегральной и дифференциальной форме (Закон полного тока). Пример вычисления магнитного поля соленоида. Силовые линии магнитного поля.Чтобы показать вихревой характер магнитного поля, надо ввести новый оператор ротор (rot) 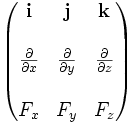 rotF= Одним из фундаментальных свойств магнитного поля является то, что  . .Это свойство выводится из теоремы Гаусса для векторного поля  в дифференциальной форме следует, что поле в дифференциальной форме следует, что поле  можно представить в виде ротора вспомогательного векторного поля можно представить в виде ротора вспомогательного векторного поля  , называемого векторным потенциалом: , называемого векторным потенциалом:  и уравнения векторного потенциала  . .Формулировка теоремы о циркуляции Пусть контур произвольной формы охватывает произвольное число токов. В этом случае теорема о циркуляции утверждает, что циркуляция вектора  по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е. по некоторому (произвольному!) контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на μ, т.е. 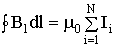 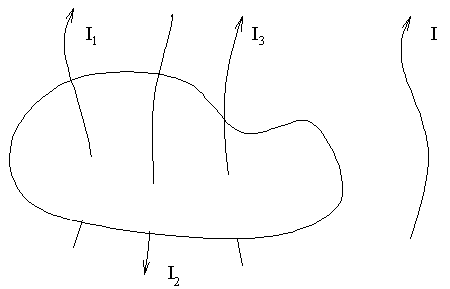 . . 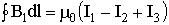 Ток I в сумму не входит! Применение теоремы о циркуляции для вычисления магнитного поля бесконечно длинного соленоида: Соленоид - провод, навитый на цилиндрический каркас. На один метр длины - n витков. В 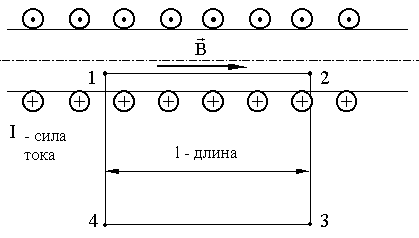 ыберем такой контур, как на рисунке, т.к. из соображений симметрии вектор ыберем такой контур, как на рисунке, т.к. из соображений симметрии вектор  может быть направлен только вдоль оси соленоида. может быть направлен только вдоль оси соленоида. Тогда 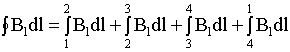 . .1) В интервалах от точки 2 до точки 3 и от точки 4 до точки 1  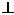 стороне контура, значит Вl = 0. стороне контура, значит Вl = 0.2) Тогда: 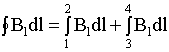 . .3) Можно показать, что вне бесконечного соленоида B=0, т.е. 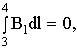 . .Значит: 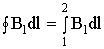 , ,т.к. внутри соленоида B = Bl = const, то 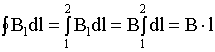 . .По теореме о циркуляции  . .Откуда магнитное поле бесконечного соленоида: 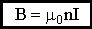 . Направлено . Направлено  вдоль оси соленоида, в соответствии с правилом правого винта. вдоль оси соленоида, в соответствии с правилом правого винта.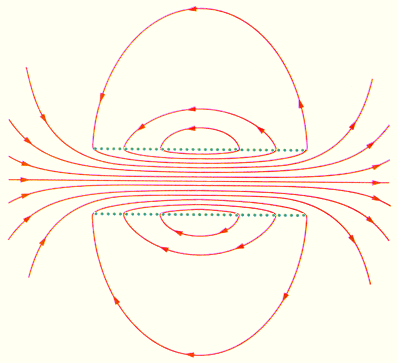 Силовые линии магнитного поля: Линии магнитного поля: а) замкнуты, т.к. в природе нет магнитных зарядов; б) вектор В направлен по касательной к линии магнитной индукции; в) густота линий магнитной индукции пропорциональна модулю вектора  12. Магнитное взаимодействие токов. Сила Ампера. Вычисление силы взаимодействия двух прямолинейных проводников с током.Магнитные явления были известны еще в древнем мире. Опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся повернуть стрелку. Французский физик ссылка скрыта наблюдал силовое взаимодействие двух проводников с токами и установил закон взаимодействия токов. По современным представлениям, проводники с током оказывают силовое действие друг на друга не непосредственно, а через окружающие их магнитные поля. Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Изолированных магнитных зарядов не существует. Магнитное поле, в отличие от электрического, оказывает силовое действие только на движущиеся заряды (токи). Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности  электрического поля. Такой характеристикой является вектор магнитной индукции электрического поля. Такой характеристикой является вектор магнитной индукции  Вектор магнитной индукции Вектор магнитной индукции  определяет силы, действующие на токи или движущиеся заряды в магнитном поле. определяет силы, действующие на токи или движущиеся заряды в магнитном поле.За положительное направление вектора  принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора  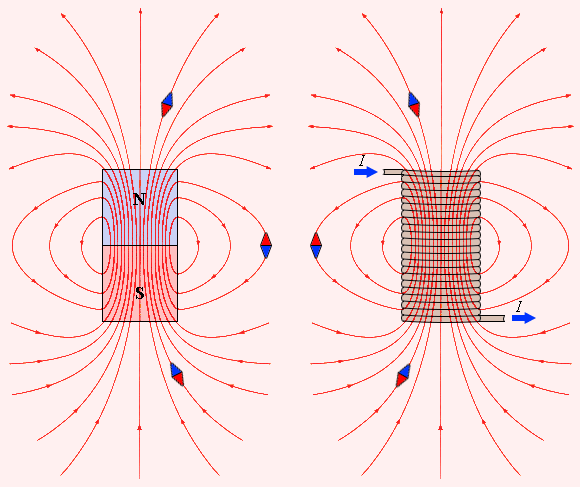 Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми.Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Как показали опыты Ампера, сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции:
Эта сила называется силой Ампера. Она достигает максимального по модулю значения Fmax, когда проводник с током ориентирован перпендикулярно линиям магнитной индукции. Модуль вектора  определяется следующим образом: определяется следующим образом:Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока I в проводнике и его длине Δl:
В общем случае сила Ампера выражается соотношением:
Это соотношение принято называть законом Ампера. В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (Тл).
Тесла – очень крупная единица. Магнитное поле Земли приблизительно равно 0,5·10–4 Тл. Большой лабораторный электромагнит может создать поле не более 5 Тл. Сила Ампера направлена перпендикулярно вектору магнитной индукции  и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки. и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки.Р 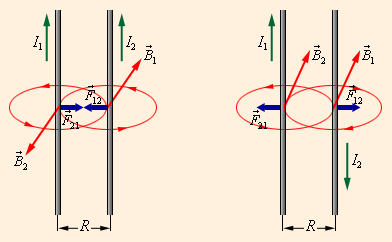 исунок слева поясняет закон взаимодействия параллельных и антипараллельных токов в прямолинейных проводниакх с током. исунок слева поясняет закон взаимодействия параллельных и антипараллельных токов в прямолинейных проводниакх с током.Магнитное взаимодействие параллельных проводников с током используется в системе СИ для определения единицы силы тока – ампера: Ампер – сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, равную 2·10–7 H на каждый метр длины. Формула, выражающая закон магнитного взаимодействия параллельных токов, имеет вид:
|



