С 2007 Группа 04-102, 2 семестр
| Вид материала | Закон |
СодержаниеПоток векторного поля Теорема Гаусса Работа по замкнутой траектории равна нулю Потенциал электростатического поля |
- Лекций студентами Кафедра биологии дисциплина ботаника группа, 75.84kb.
- Темы рефератов по дисциплине: «Оcновы аудита» Сущность аудиторской деятельности, 153.15kb.
- Курс, группа у-5360, срок обучения 4 года 4 месяца, осенний семестр 2007-2008 учебного, 158.22kb.
- Список публикаций педагогов моу сош №102 в 2007-2008 учебном году, 38.48kb.
- Году в Республике Коми составил 103,0% к уровню 2007 года, что выше среднероссийского, 240.16kb.
- График контрольных мероприятий по учебным дисциплинам III курс I семестр группа 3394,3395, 94.19kb.
- Анализ ситуации на рынке производства сахара, 81.6kb.
- Сп 41-102-98, 1743.38kb.
- Никитина Ирина Александровна, д э. н., профессор, sizn@mail ru Бакалаврская программа, 154.15kb.
- Курс 5 Семестр: 9-10 Астана 2011 7 Сведения о преподавателях, 325.38kb.
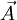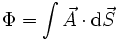2. Поток вектора напряженности электростатического поля. Теорема Гаусса и ее применение к расчету напряженности полей. Поле бесконечной равномерно заряженной плоскости. Поле заряженной сферы и заряженного шара. Поле бесконечной равномерно заряженной нити. Дифференциальная форма теоремы Гаусса.Поток ссылка скрыта - поток Φ ссылка скрыта  через ссылка скрыта S - интеграл по поверхности ,при этом векторный элемент площади поверхности определяется как 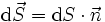 ,где 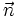 - ссылка скрыта, нормальный к поверхности.Теорема Гаусса ссылка скрыта ссылка скрыта через любую, произвольно выбранную, замкнутую поверхность равен алгебраической сумме заключённых в этой поверхности ссылка скрыта, делённой на ссылка скрыта ε0 : 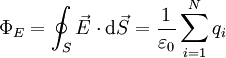 .Данное выражение представляет собой теорему Гаусса в интегральной форме. В дифференциальной форме теорема Гаусса выражается следующим образом: 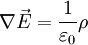 ,где ρ — объёмная плотность заряда 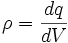 .Теорема Гаусса выражает связь между потоком напряженности электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью. Физической основой теоремы Гаусса является ссылка скрыта или, иначе, теорема Гаусса является интегральной формулировкой ссылка скрыта. 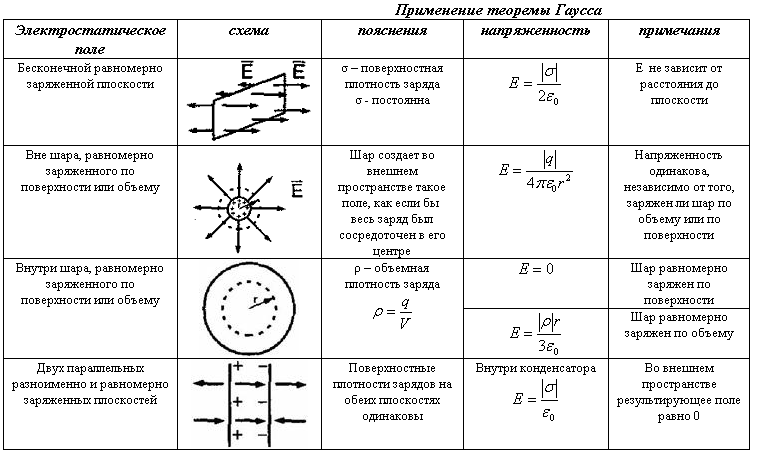 3. Работа сил электростатического поля при перемещении зарядов. Потенциальный характер электростатического поля. Циркуляция вектора напряженности электростатического поля. Потенциал электростатического поля. Потенциал поля точечного заряда. Связь между напряженностью и потенциалом. Эквипотенциальные поверхности.Работа электростатического поля (A) A = Fd=qEd,
A1 = Fd1 cos , но d1 cos = d, A1 = qEd A = A1 A1,2,3,1 = A1,2 + A2,3 + A3,1 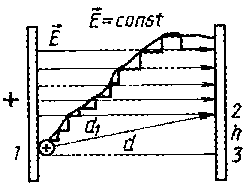 A1,2,3,1 = qEd1 cos a + Eqh cos 90° + Eqd cos 180° = qEd + 0 + ( - qEd) A1,2,3,1 =0 т. е. работа при перемещении заряда между двумя точками в электростатическом поле не зависит от формы траектории, а зависит от положения этих точек. Работа по замкнутой траектории равна нулю. Электростатическое поле, как и гравитационное, потенциальное. Электростатические силы, как и гравитационные, относятся к консервативным (потенциальным) силам. Работа консервативных сил равна изменению потенциальной энергии взятому с противоположным знаком. A = Ai = (W2 W1) = Wп
Потенциальная энергия W заряда q в однородном электростатическом поле напряженностью E на расстоянии d от 0 потенциального уровня Wп = Eqd Потенциальность электростатического поля. Электрический потенциал Р 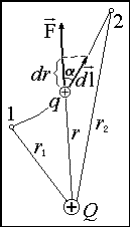 абота поля по переносу пробного q заряда из некоторой точки 1 в некоторую точку 2 не зависит от траектории его движения и определяется для данного поля и данного заряда только координатами этих точек. Для случая, когда источником поля является точечный заряд Q (рис. 1.6.1) это нетрудно обосновать следующим образом. Работа на элементарном отрезке траектории, по известному из механики определению, есть:  . Раскрывая скалярное произведение векторов через угол между ними, получаем . (1.6.1)Суммируя (интегрируя) все элементарные работы, находим  , (1.6.2)что и требовалось доказать. Работа определяется только расстояниями от источника до начальной и конечной точки траектории. Такое силовое поле в механике мы называли потенциальным. Из принципа суперпозиции следует потенциальность электростатического поля, созданного любой системой зарядов. Из (1.6.2) и принципа суперпозиции следует также, что работа электростатических сил над зарядом, перемещаемым по замкнутому контуру, равна 0:  . (1.6.3)Таким образом, для любого контура в электростатическом поле циркуляция напряженности – тождественный нуль. В соответствии с утверждением (1.5.6) напряженность электростатического поля (с точностью до знака) может быть истолкована как градиент некоторой функции координат, называемой потенциалом электростатического поля  : . (1.6.4)Используя определение напряженности электростатического поля и формулу связи между силой F и потенциальной энергией W, известную из курса механики  , (1.6.5)из (1.6.4) получим, что потенциал поля в данной точке наблюдения численно равен потенциальной энергии пробного заряда q, помещаемого в данную точку, отнесенной к величине этого заряда:  .Иначе говоря, поле, работа которого при перемещении заряда по любой замкнутой траектории равна нулю, называют потенциальным. Пример потенциального поля — электростатическое поле. Потенциал В качестве энергетической характеристики поля в данной точке используют потенциал Потенциал электростатического поля — отношение потенциальной энергии заряда в поле к этому заряду: 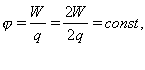 Выражается потенциал в вольтах: 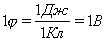 Потенциал не зависит от заряда q, помещенного в данную точку поля. Для однородного поля 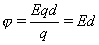 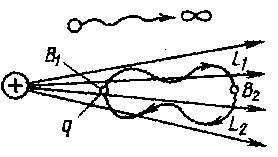 потенциал зависит от напряженности E и от расстояния d от данной точки поля до нулевого потенциального уровня. Работа поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность характеризует потенциал в данной точке поля созданного точечным зарядом Q смотри рисунок выше, 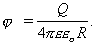 где Q — заряд создающий поле, R — расстояние от данной точки поля до заряда Q. Потенциальная энергия электрического взаимодействия системы n точечных зарядов qi равна Wп = 1/2qi i здесь i — потенциал поля в точке, где находится заряд qi Если поле создано двумя зарядами, то выполняется следствие принципа суперпозиции полей. = 1 + 2 Потенциал поля, созданного несколькими заряженными телами, равен алгебраической сумме потенциалов отдельных полей, создаваемых в данной точке пространства каждым из заряженных тел: = 1 + 2 n Эквипотенциальные поверхности Поверхность, все точки которой имеют одинаковый потенциал, называют эквипотенциальной.
если = 90 , то A = 0 1 = 2 = 3 = 4 Силовые линии перпендикулярны такой поверхности . |