Лекция №13. Индуктивно-связанные цепи. Эдс взаимной индукции. Последовательное и параллельное соединение индуктивно-связанных катушек. Расчет сложных индуктивно-связанных цепей

Вид материала

Лекция

Содержание Воздушный (линейный) трансформатор Б Рис.7. аланс мощностей в цепях с индуктивно связанными элементами

Подобный материал:

• План занятий студентов 2 курса 3 семестр 1 лекционный курс, 72.01kb.
• Лекция n 11, 759.84kb.
• Список поступивших и принятых редколлегией докладов на XIV чтения им. А. Н. Заварицкого, 85.9kb.
• Общая характеристика задач, относящихся к теории электрических и электронных цепей,, 50.16kb.
• Задача № расчет линейной электрической цепи постоянного тока по заданной обобщенной, 87.8kb.
• Современные способы пробоподготовки для спектральных методов анализа экологических, 200.11kb.
• Программа вступительных экзаменов в магистратуру по специальности 6М071800 «Электроэнергетика», 590.06kb.
• Контрольная работа выполняется на тему «Основные законы теории цепей, анализ установившегося, 35.6kb.
• Расчет сложных цепей постоянного тока, 93.75kb.
• Лекция расчет сложных цепей постоянного тока. Метод узловых потенциалов, 8.34kb.

Лекция №13. Индуктивно-связанные цепи. ЭДС взаимной индукции. Последовательное и параллельное соединение индуктивно-связанных катушек. Расчет сложных индуктивно-связанных цепей.
Метод уравнений Кирхгофа, метод контурных токов.


И
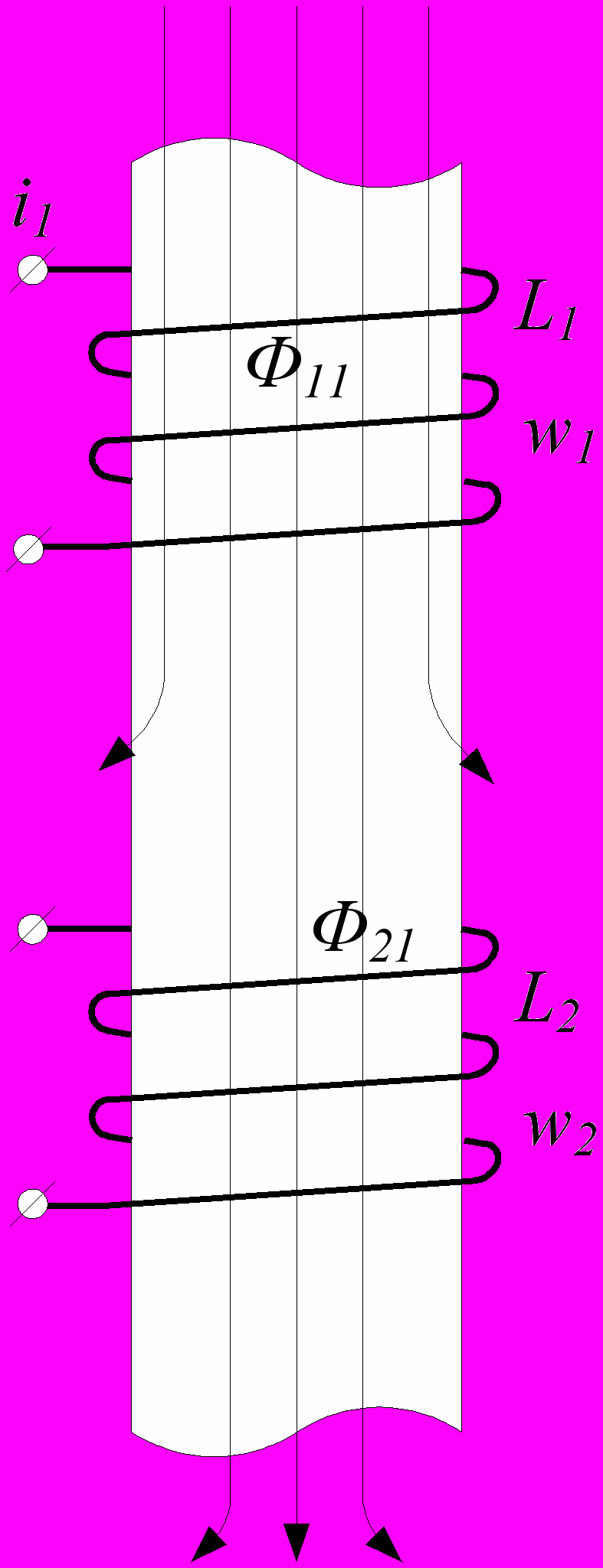Рис.1.
ндуктивно-связанными называются такие цепи, которые содержат индуктивные элементы, охваченные общим магнитным потоком. Подобно тому, как явление самоиндукции количественно характеризуется индуктивностью L цепи, явление взаимной индукции контуров определяется взаимной индуктивностью М проводящих цепей. Под величиной взаимной индуктивности или коэффициента взаимоиндукции М контуров 1 и 2 понимают общий для этих контуров поток магнитной индукции (т. е. число тех линий магнитной индукции, которые пронизывают площади, ограниченные обоими контурами), когда в одном из контуров протекает ток, равный единице (рис. 1). Поскольку напряженность магнитного поля в любой точке пропорциональна величине тока, создающего поле, то и магнитный поток Ф₁ создаваемый током i₁ который протекает в контуре 1, пропорционален току i₁ (причем коэффициент пропорциональности представляет собой индуктивность L₁ контура 1) Часть Ф₁₂ упомянутого магнитного потока, пронизывающая контур 2, очевидно, также пропорциональна току i₁: 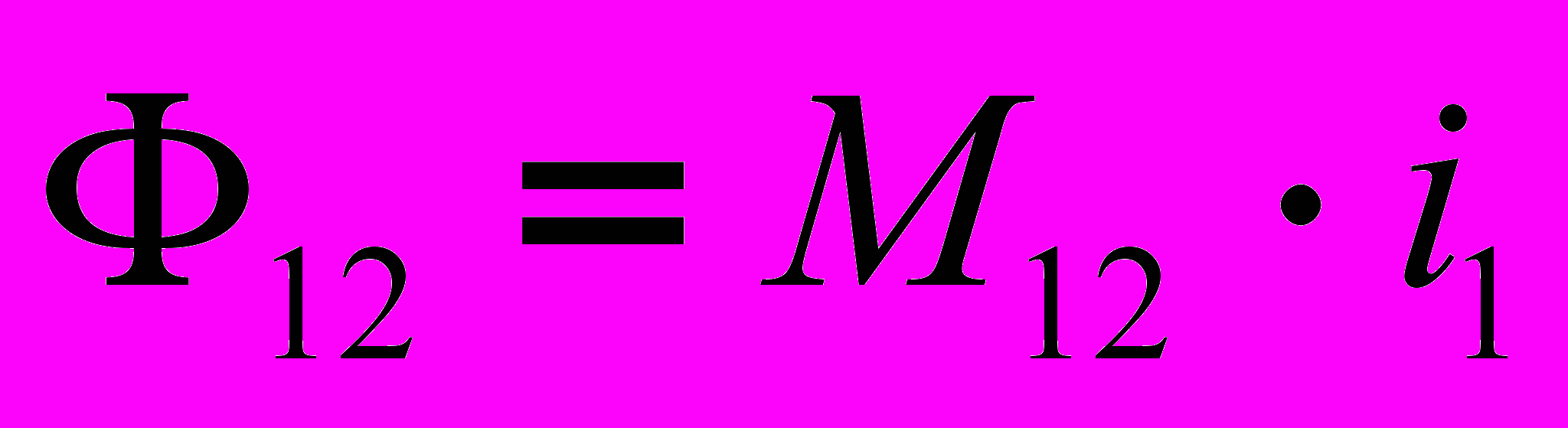, причем коэффициент пропорциональности М₁₂ представляет собой взаимную индуктивность контуров 1 и 2. Поскольку через контур 2 проходит ток i₂, то для величины общего магнитного потока, создаваемого током i₂ и пронизывающего контур 1 рассуждая аналогично, мы можем написать выражение: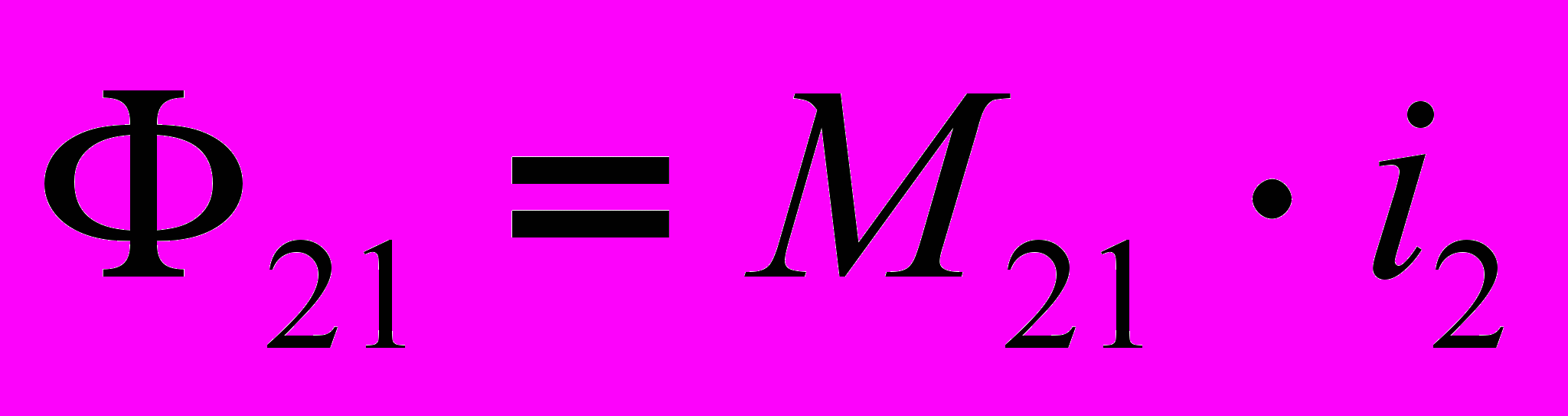Нетрудно доказать, что коэффициент пропорциональности в этой формуле тождествен коэффициенту пропорциональности в предыдущей формуле, т. е. представляет собой ту же самую взаимную индуктивность контуров: ,.

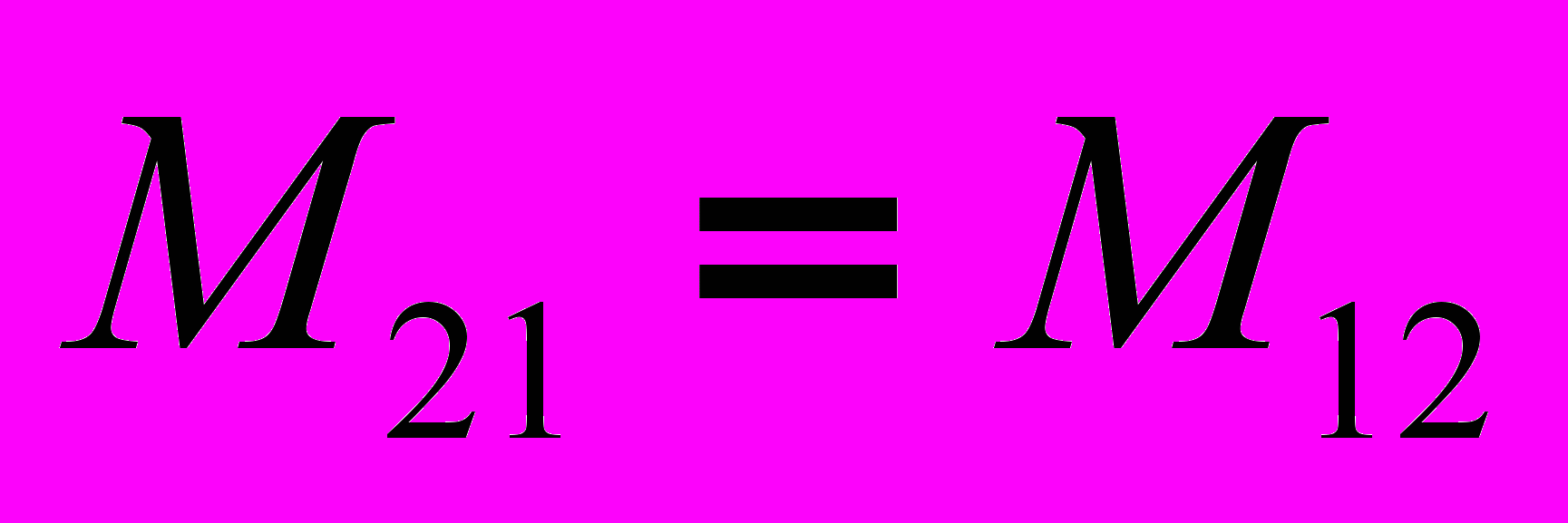Электрические цепи могут содержать такие индуктивно связанные друг с другом элементы. Эти элементы могут связывать цепи, электрически (гальванически) разделенные друг от друга.

В том случае, когда изменение тока в одном из элементов цепи приводит к появлению ЭДС в другом элементе цепи, говорят, что эти два элемента индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции. Степень индуктивной связи элементов характеризуется коэффициентом связи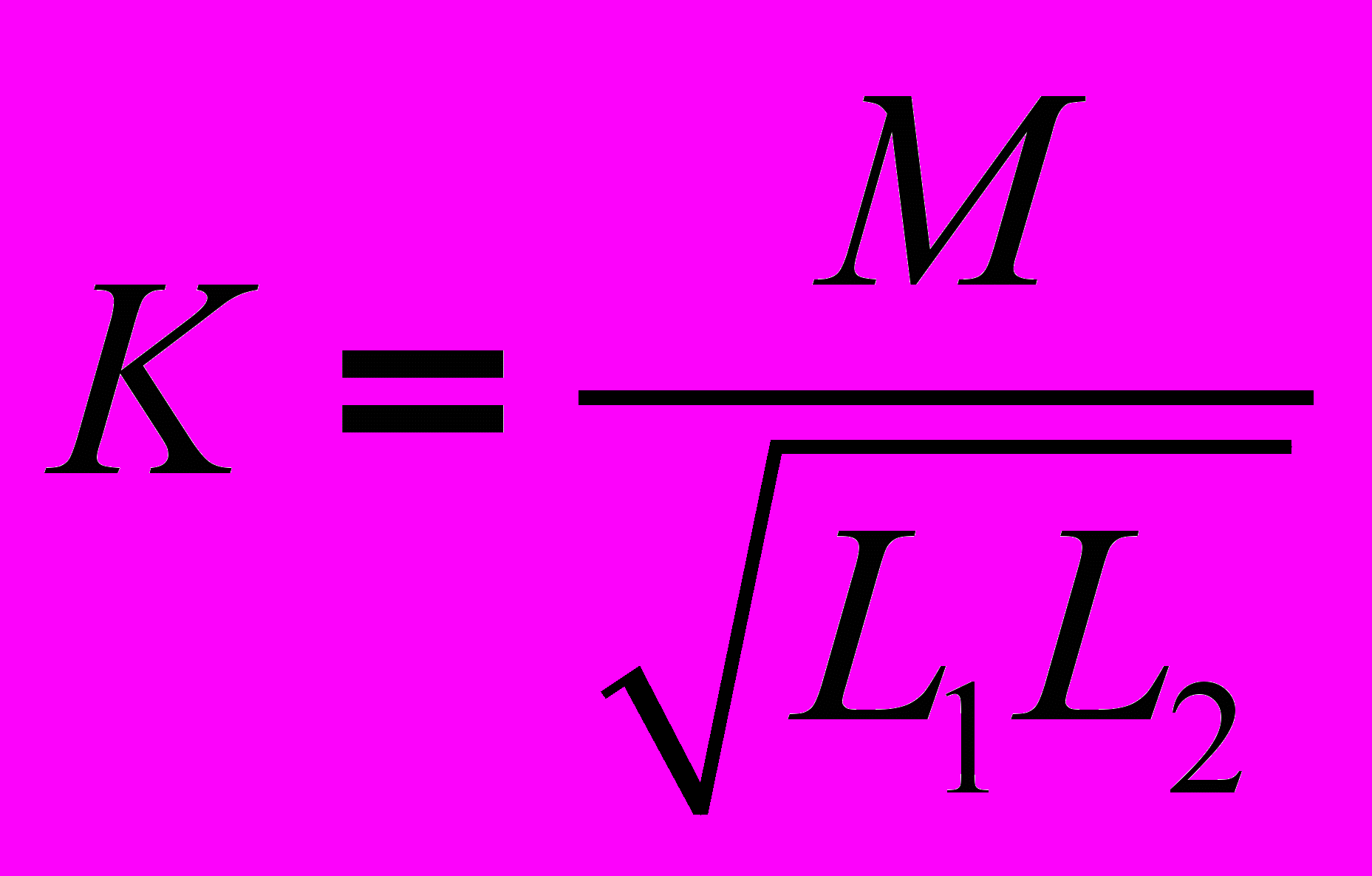, (1) где М – взаимная индуктивность элементов цепи (размерность – Гн); L₁ и L₂-собственные индуктивности этих элементов. Следует отметить, что всегда K<1. Пусть имеем две соосные катушки в общем случае с ферромагнитным сердечником (см. рис. 1). На рис. 1 схематично показана картина магнитного поля при наличии тока i₁ в первой катушке (направление силовых линий магнитного потока определяется по правилу правого буравчика). Витки первой катушки сцеплены с магнитным потоком самоиндукции Ф₁₁, а витки второй катушки – с магнитным потоком взаимной индукции Ф₂₁, который отличается от Ф₁₁ (Ф₂₁< Ф₁₁) за счет потоков рассеяния.

По определению 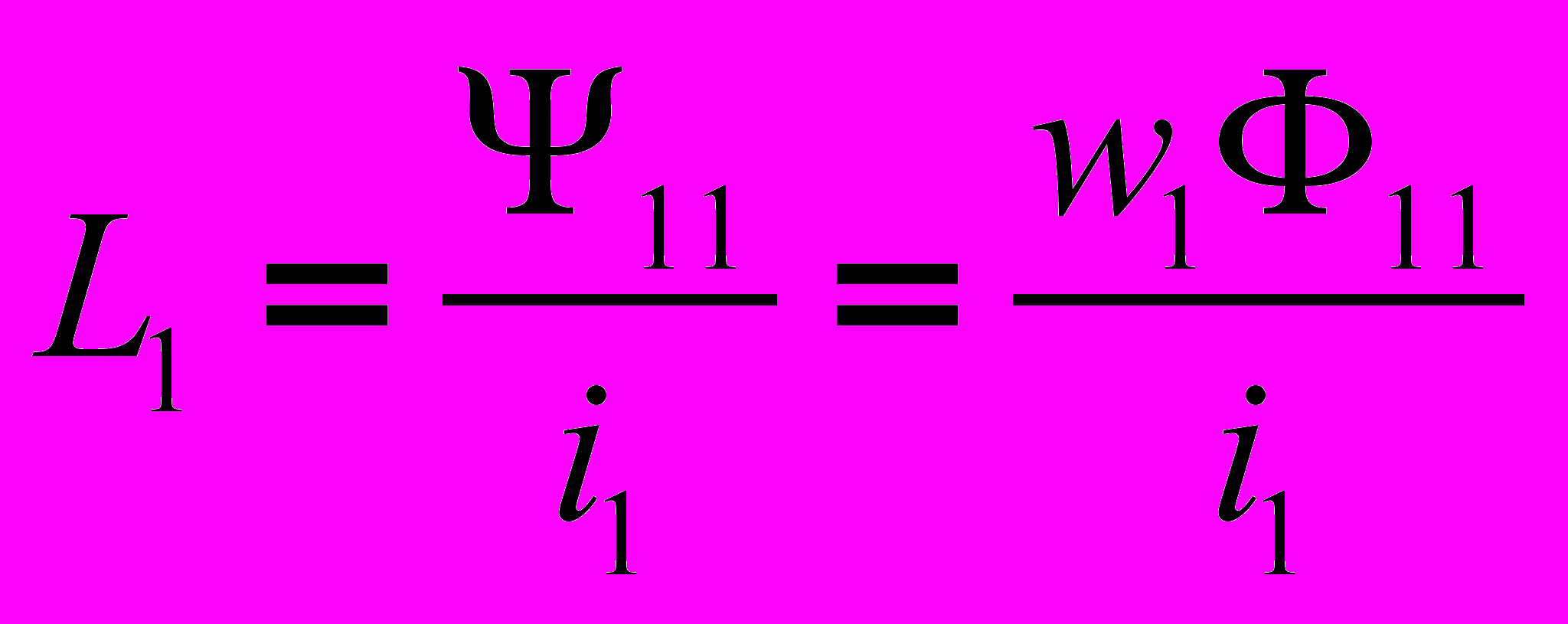(2), 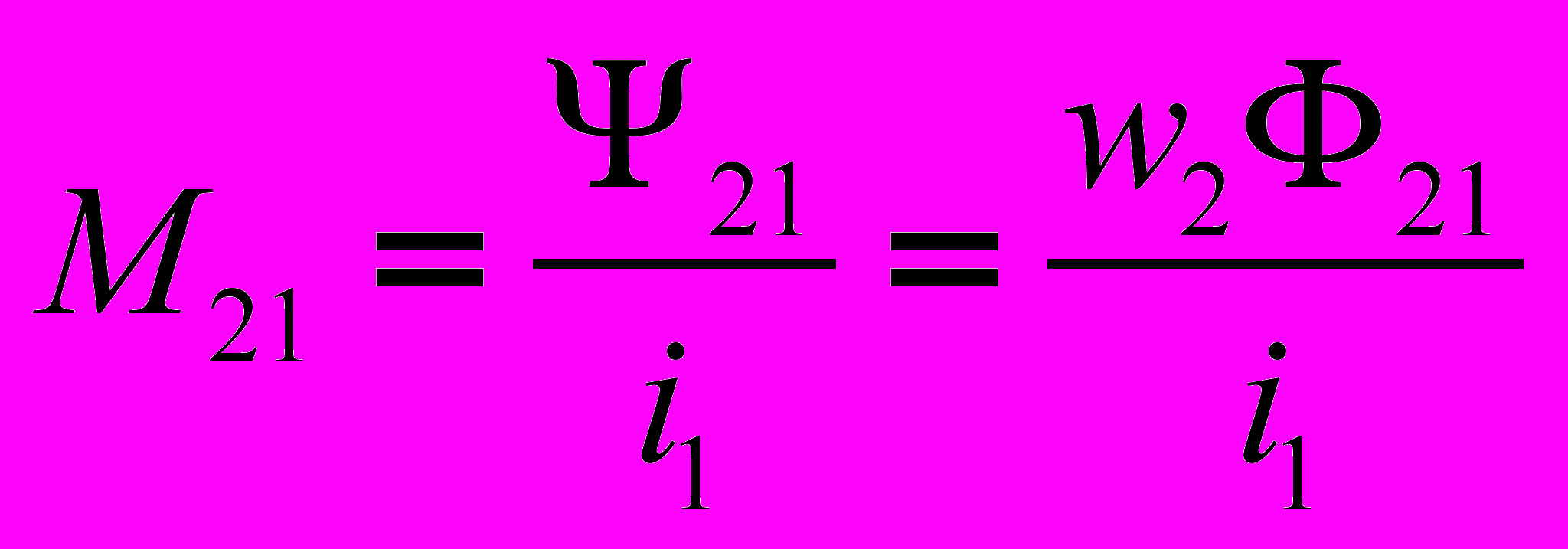(3). Если теперь наоборот пропустить ток i₂ по второй катушке, то соответственно получим 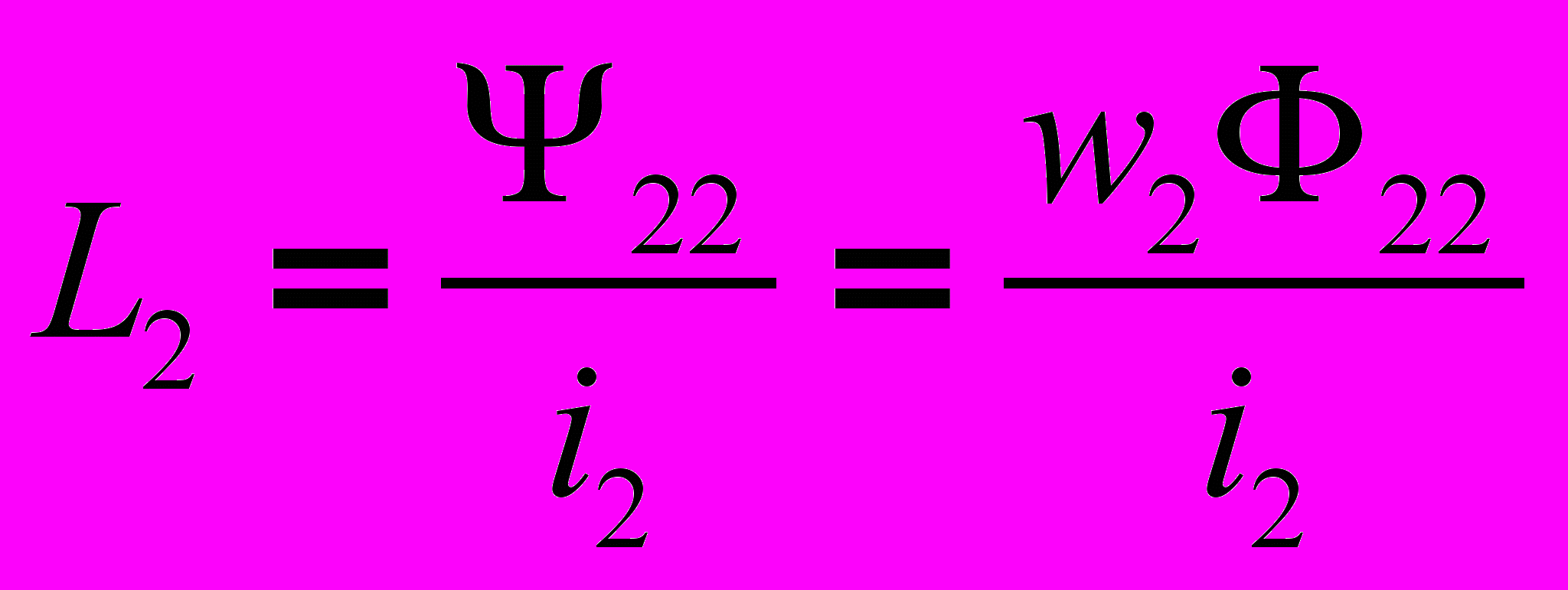(4), 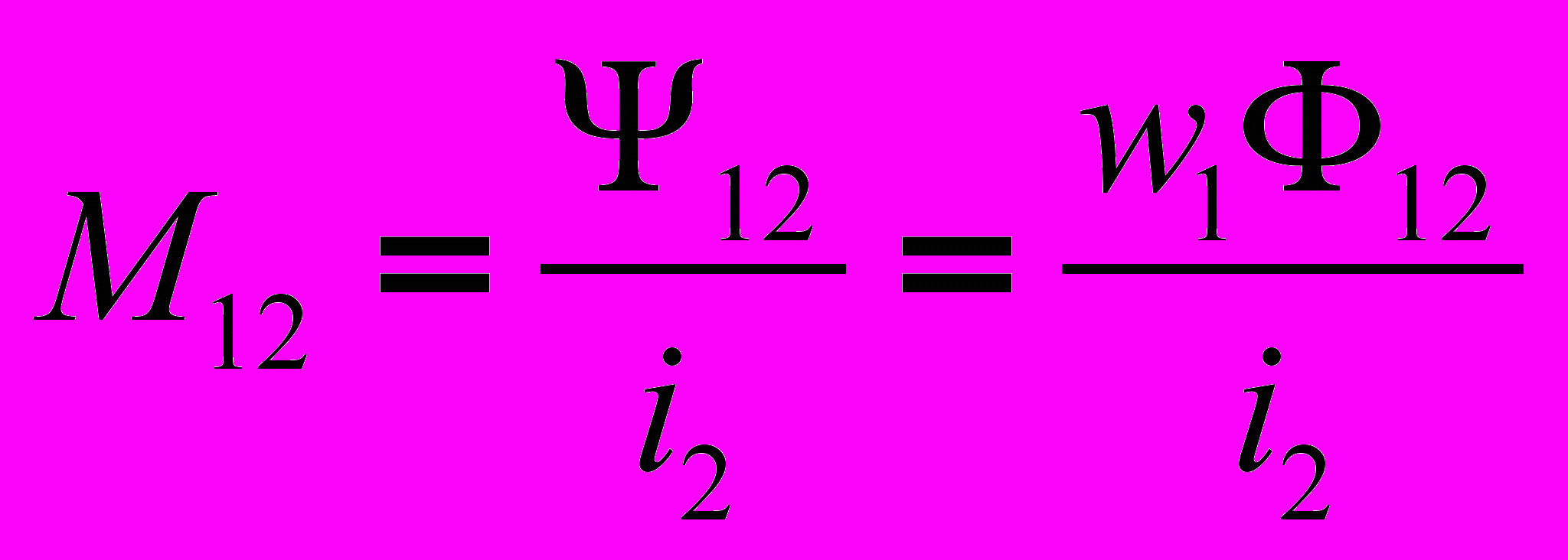(5). При этом 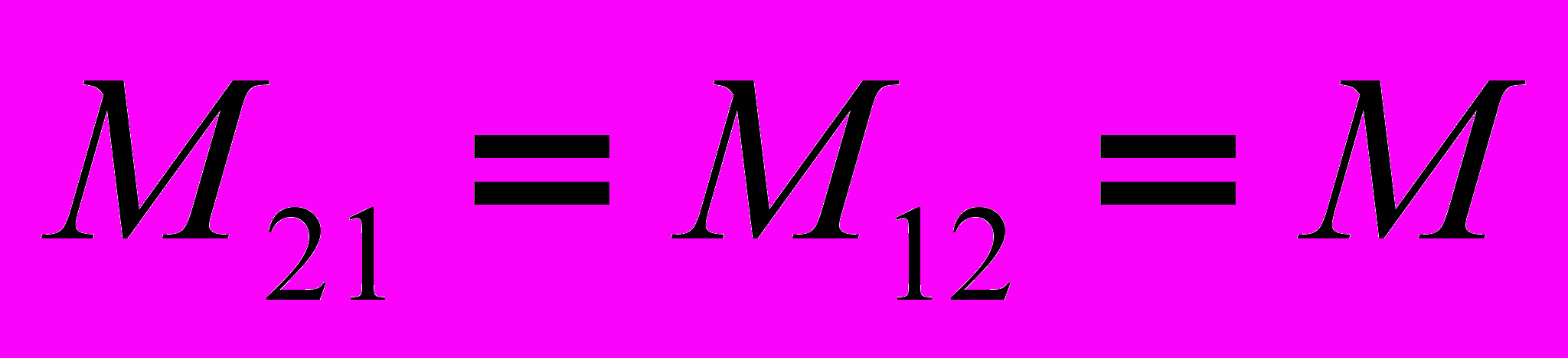(6).

Следует отметить, что коэффициент связи мог бы быть равным 1, если бы 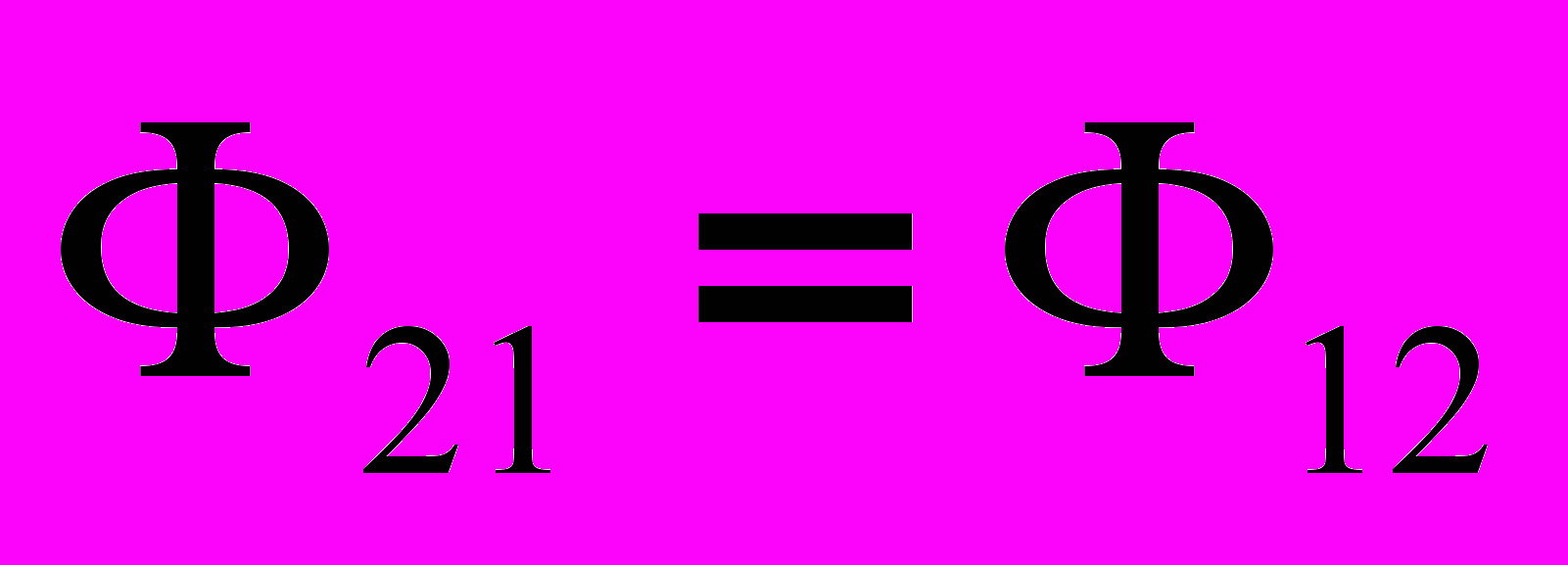и, то есть когда весь поток, создаваемый одной катушкой, полностью пронизывал бы витки другой катушки. Практически даже различные витки одной и той же катушки пронизываются разными потоками. Поэтому с учетом рассеяния  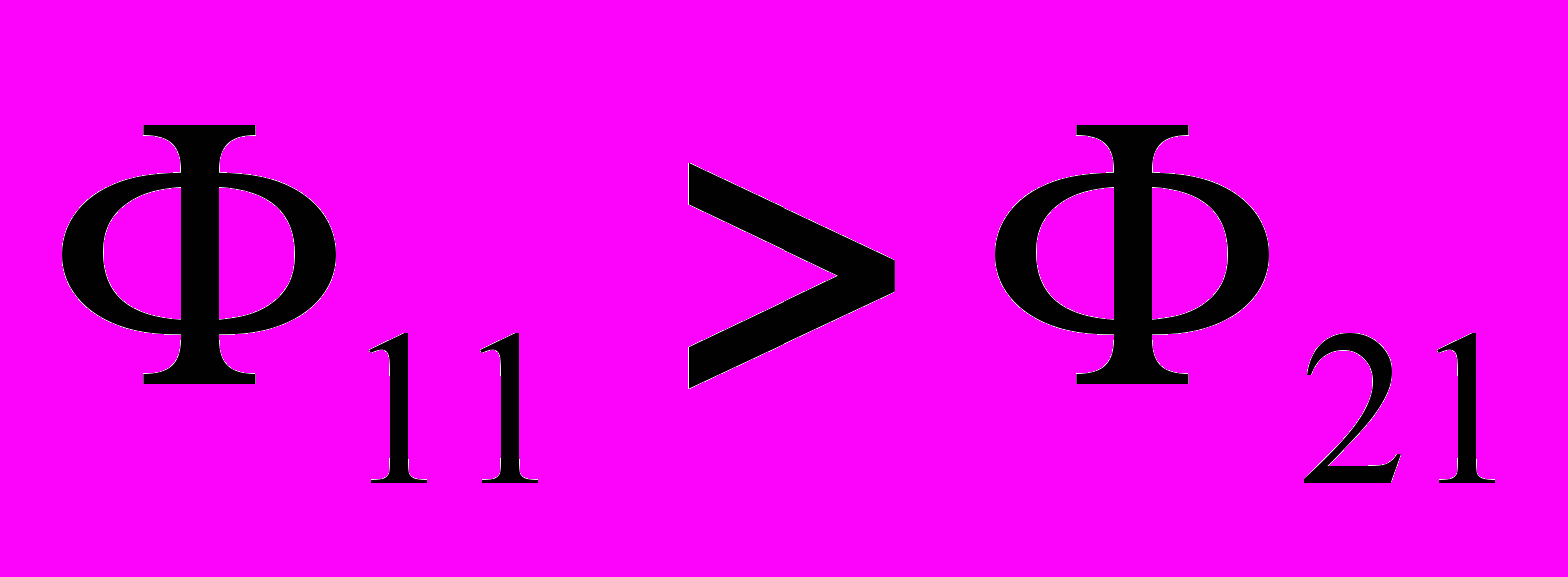и 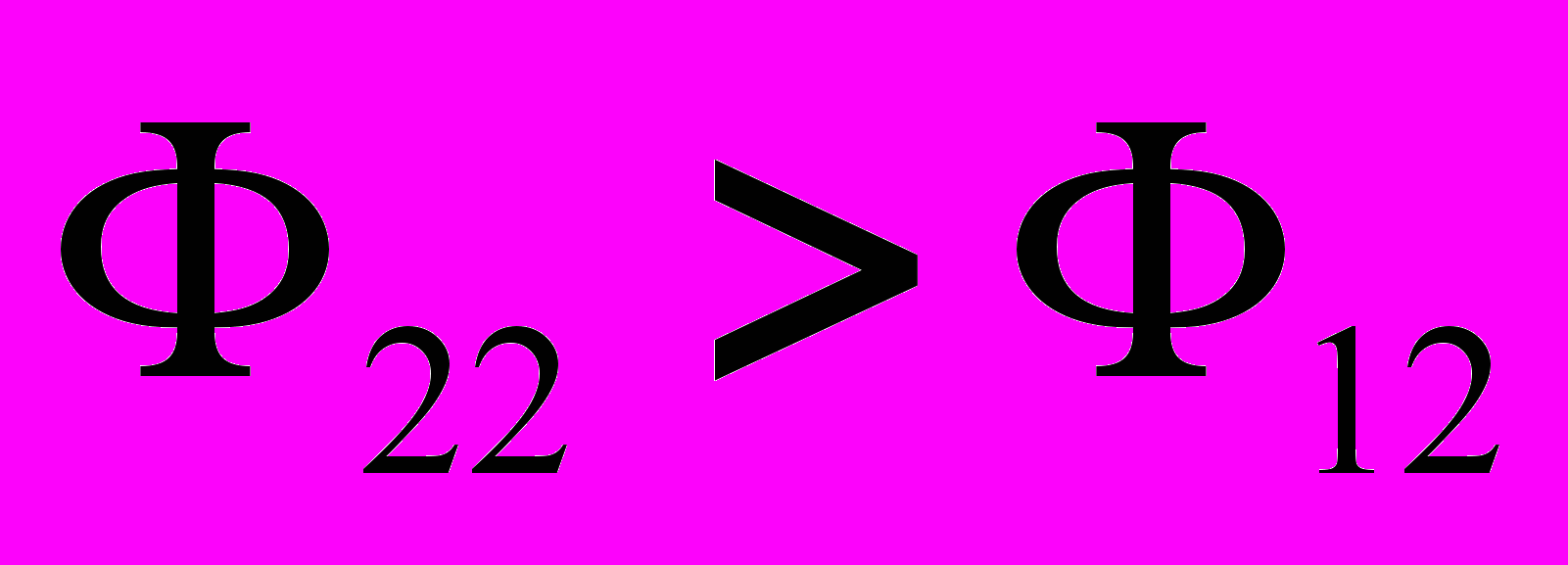. В этой связи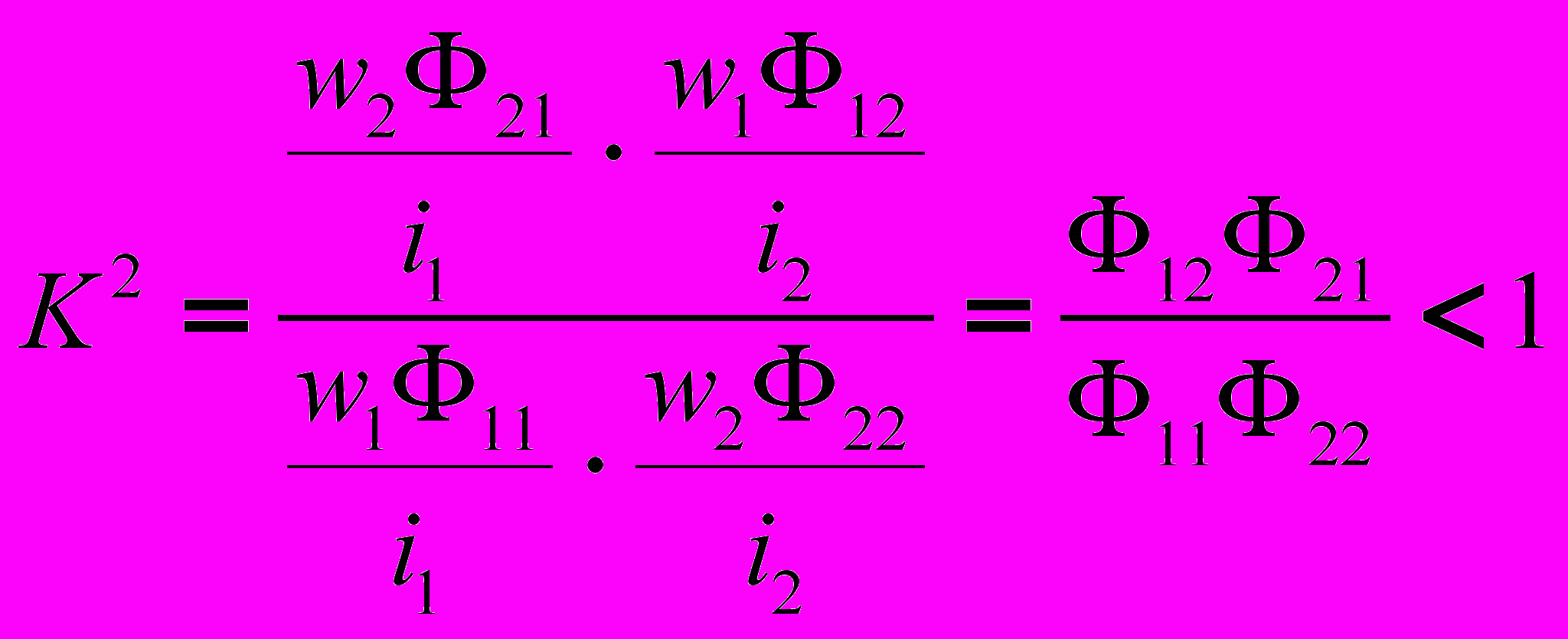



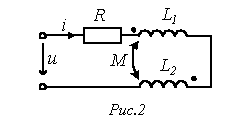
Рассмотрим цепь переменного тока на рис. 2, в которую последовательно включены две катушки индуктивности L₁ и L₂, индуктивно связанные друг с другом, и резистор R.

При изменении тока i в цепи в катушках индуцируются ЭДС само- и взаимоиндукции. При этом ЭДС взаимной индукции должна по закону Ленца иметь такое направление, чтобы препятствовать изменению потока взаимной индукции. Тогда, если в цепи протекает гармонически изменяющийся ток 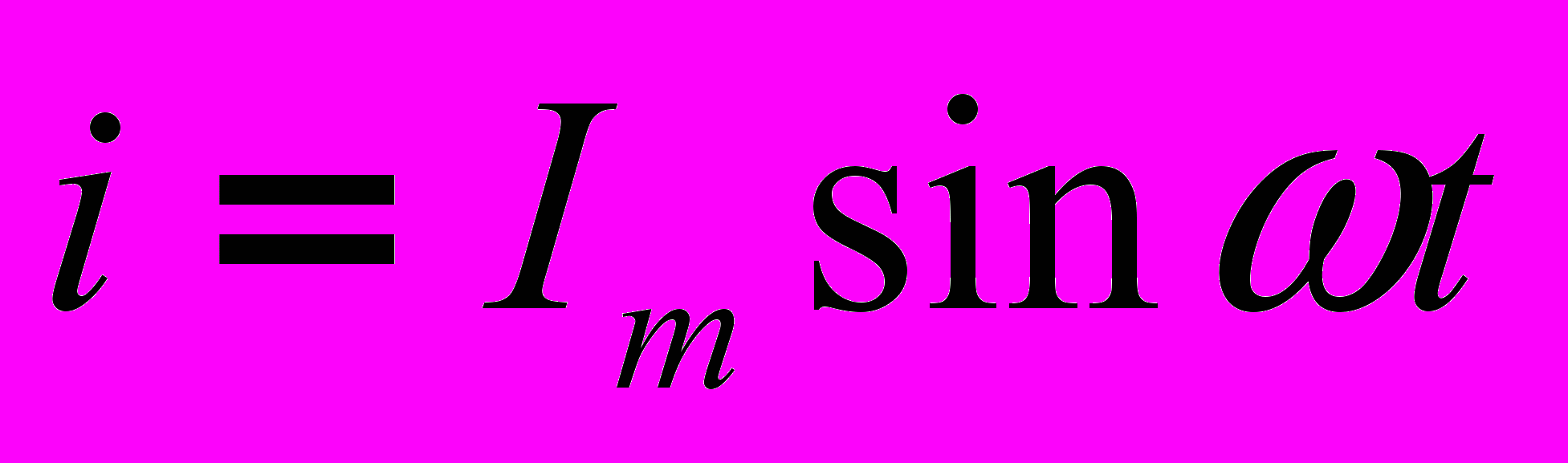, то в первой катушке индуцируется ЭДС 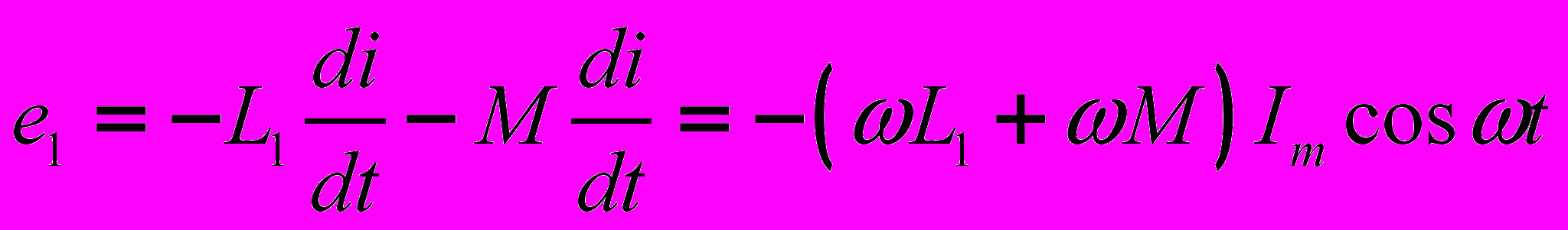(7), а во второй – 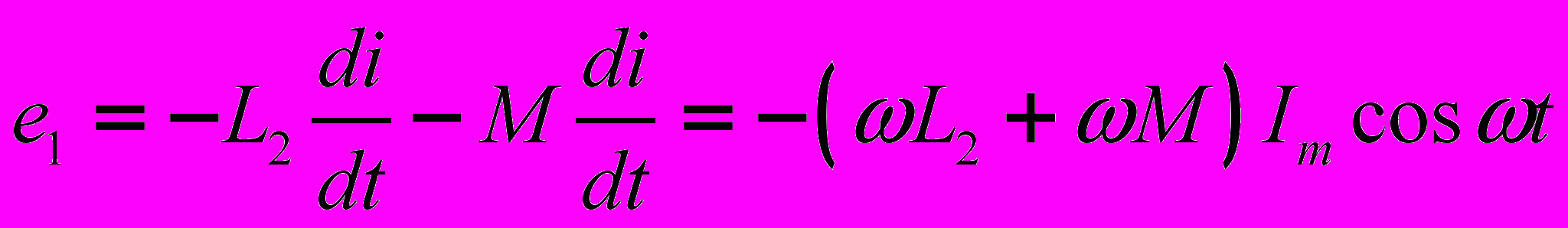(8). Катушки можно включить так, что ЭДС самоиндукции будет суммироваться с ЭДС взаимоиндукции; при переключении одной из катушек ЭДС взаимоиндукции будет вычитаться из ЭДС самоиндукции. Один из зажимов каждой катушки на схеме помечают, например точкой или звездочкой. Этот знак означает, что при увеличении, например, тока в первой катушке, протекающего от точки, во второй катушке индуцируется ЭДС взаимоиндукции, действующая от другого конца к точке. Различают согласное и встречное включения катушек. При согласном включении потоки, создаваемые каждой из катушек направлены в одну сторону. Также при согласном включении токи в катушках одинаково ориентированы по отношению к их одноименным зажимам. При этом ЭДС само- и взаимоиндукции складываются – случай, показанный на рис. 2. При встречном включении катушек потоки направлены в противоположные стороны, а токи ориентированы относительно одноименных зажимов различно. В этом случае ЭДС само- и взаимоиндукции вычитаются. Таким образом, тип включения катушек (согласное или встречное) определяются совместно способом намотки катушек и направлении токов в них.

Перейдя к комплексной форме записи (7) и (8), получим 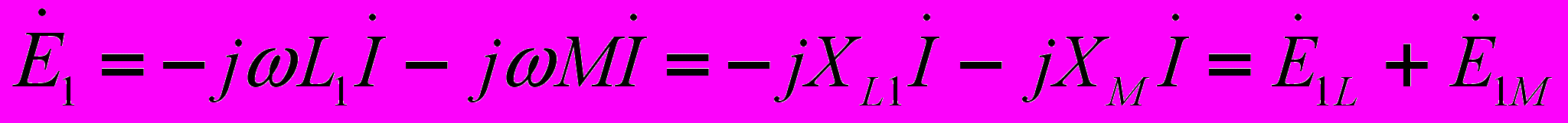(9), 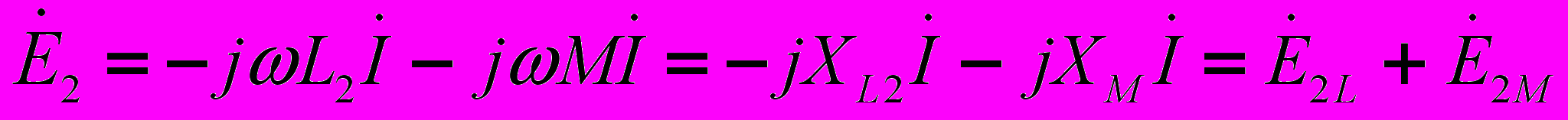(10), где 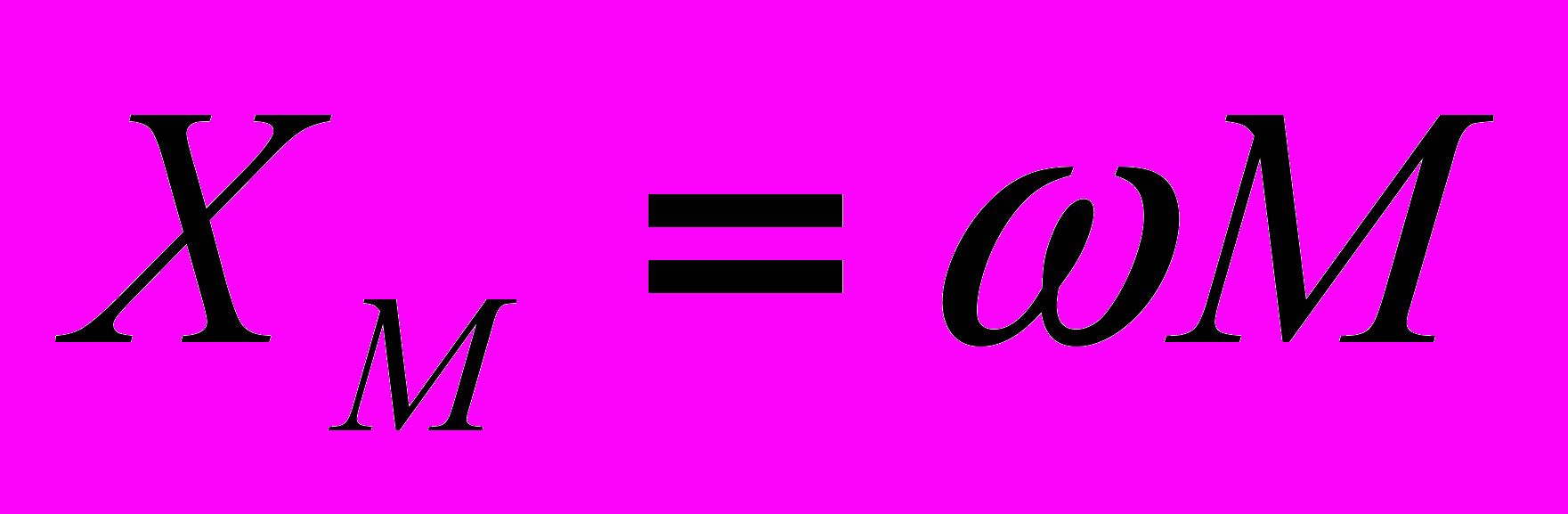- сопротивление взаимоиндукции (Ом).

Для определения тока в цепи на рис. 2 запишем 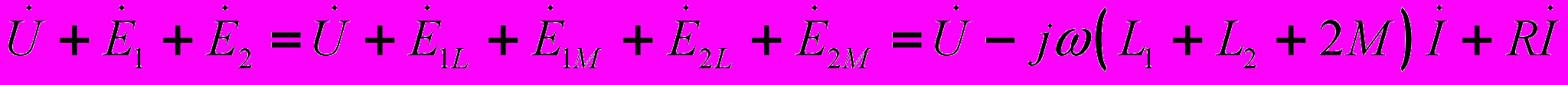откуда .

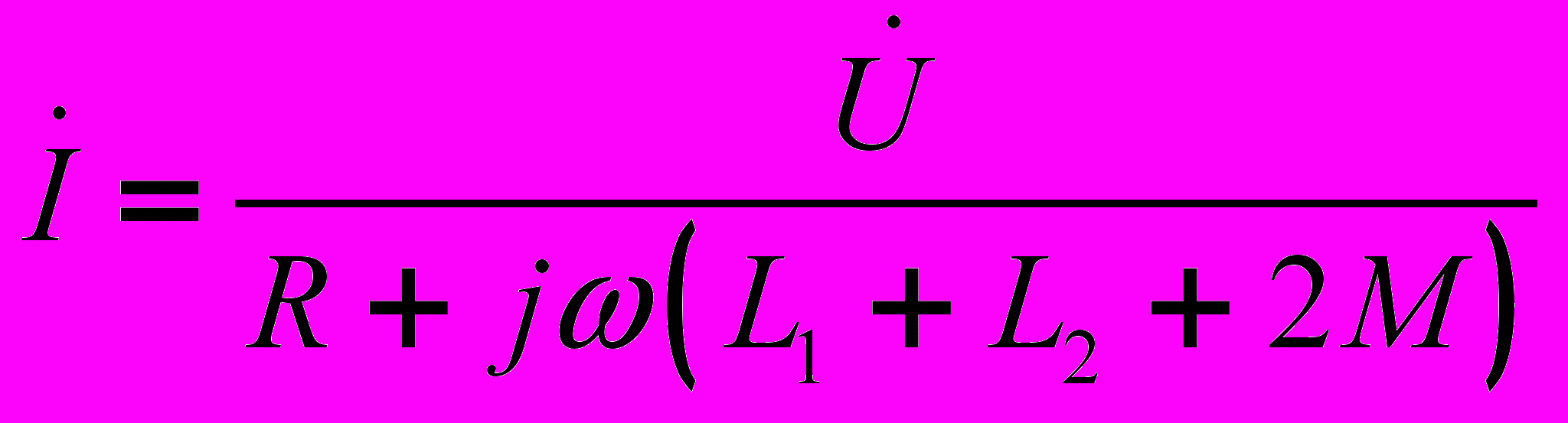Векторные диаграммы для согласного и встречного включения, построенные согласно уравнению (2), приведены на рис.2.1а,б.



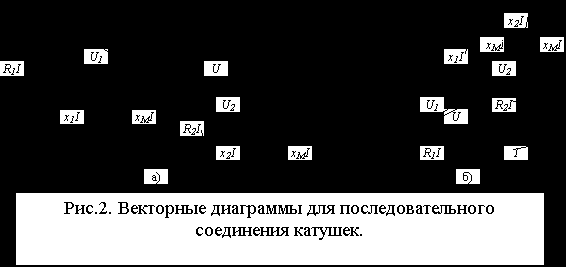
Рис.3.

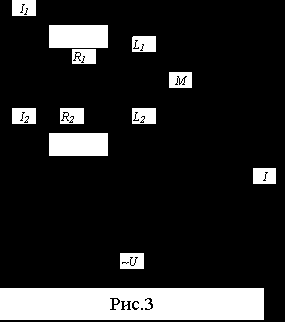Параллельное соединение катушек (рис. 3)

Уравнения, составленные по I и II за­конам Кирхгофа:

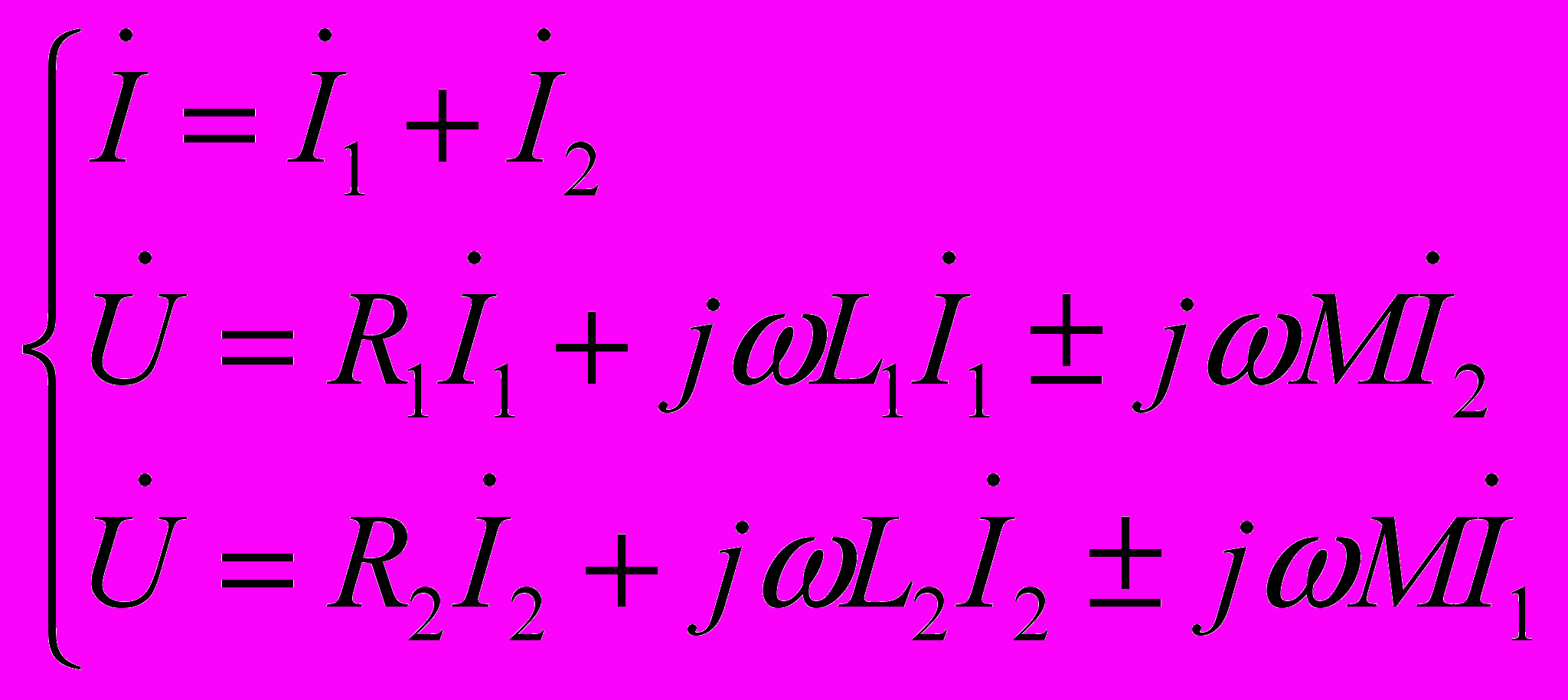(4)

Решая систему (4), можно получить


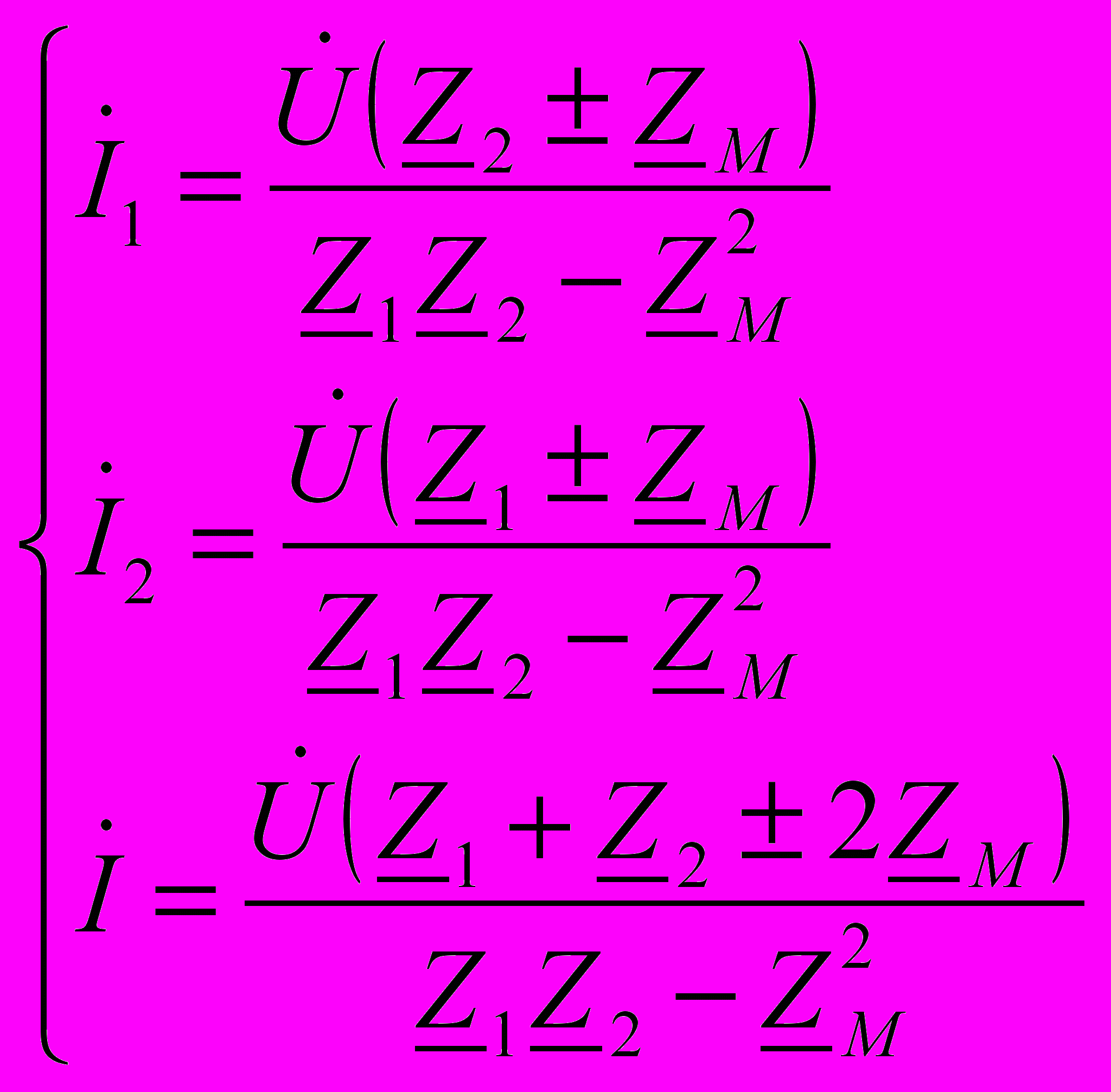
Рис.4.
(10)

Тогда 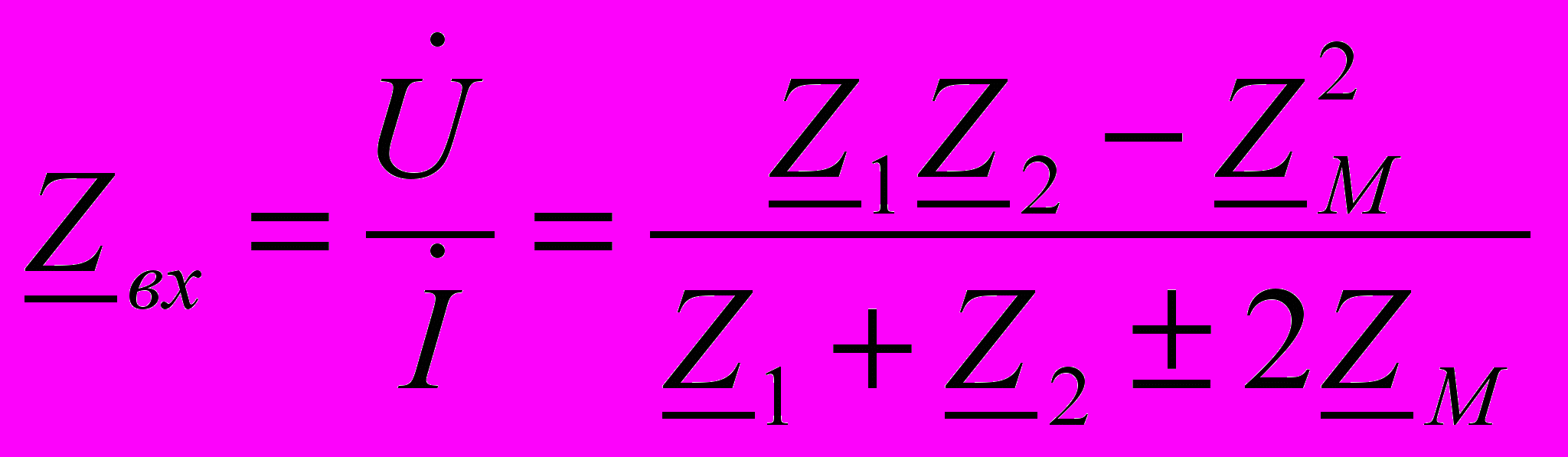(11)

Знак “ - “ в числителе в уравнениях (10) и в знаменателе уравнения (11) перед слагаемым 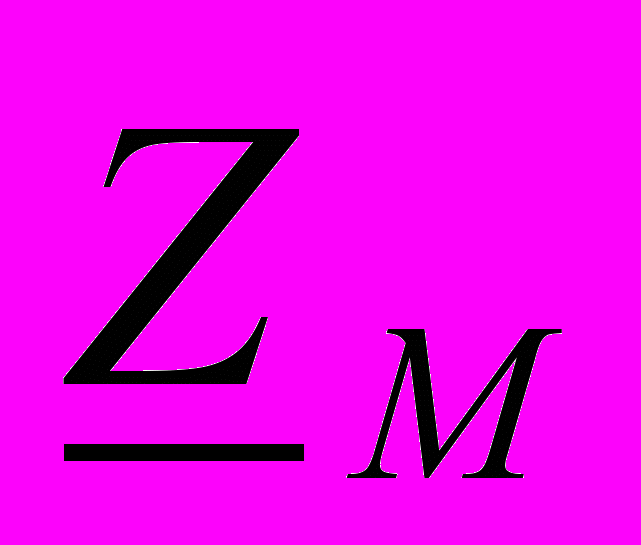  соответствует согласному, а знак "+" встречному включению. Формулу для эквивалентной индуктивности L_э получают из выражения (11). Например, при :

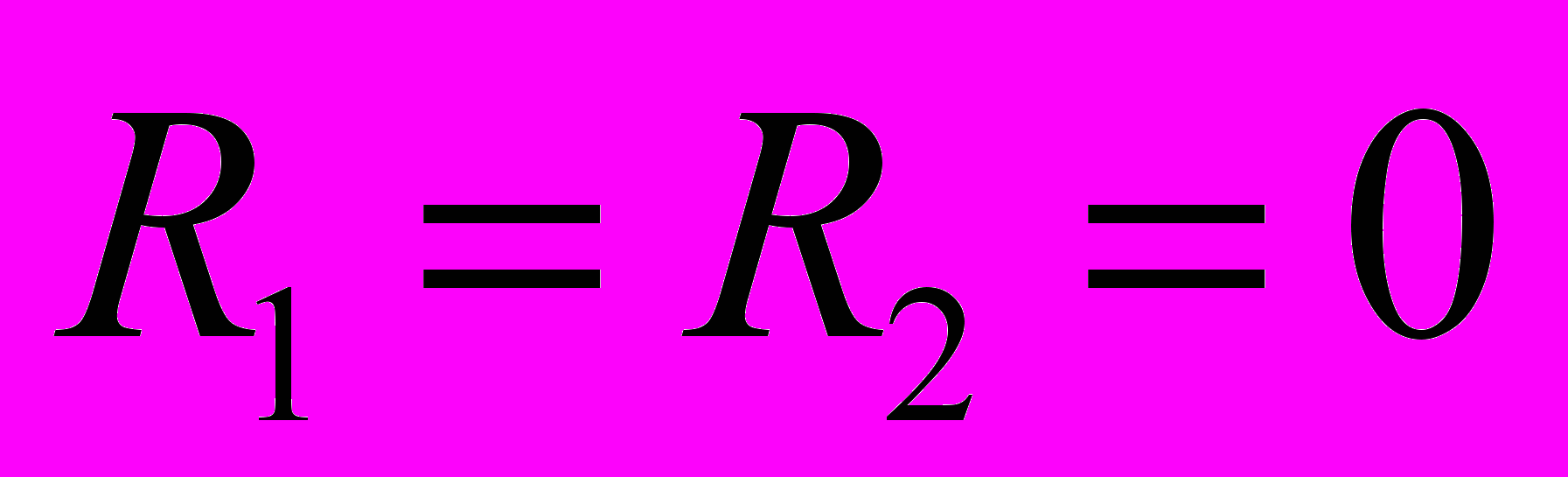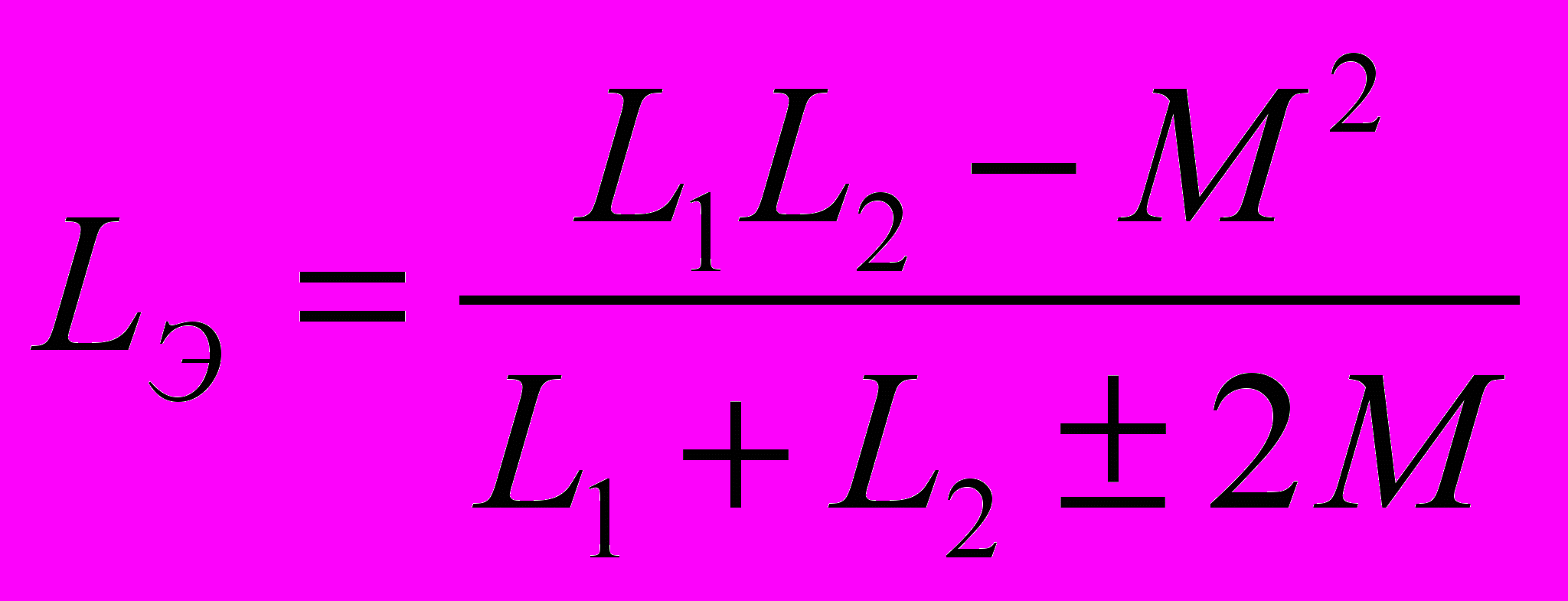(12). Векторные диаграммы для согласного и встречного включений приведены на рис.5а,б.


Рис.5.

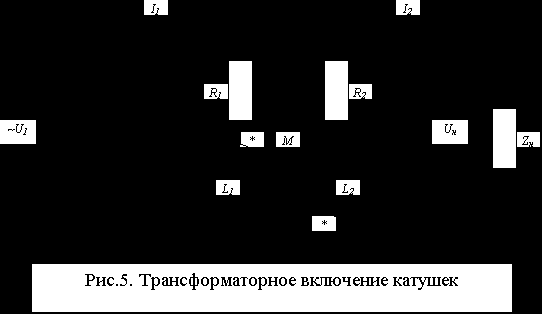
Воздушный (линейный) трансформатор

Одним из важнейших элементов электрических цепей является трансформатор, служащий для преобразования величин токов и напряжений. В простейшем случае трансформатор состоит из двух гальванически несвязанных и неподвижных катушек без ферромагнитного сердечника. Такой трансформатор называется воздушным. Он является линейным. Наличие ферромагнитного сердечника обусловило бы нелинейные свойства трансформатора.

Н
Рис.6.
а рис. 6 представлена схема замещения трансформатора, первичная обмотка которого включена на напряжение U1, а от вторичной обмотки получает питание приемник с сопротивлением .

В трансформаторе энергия из первичной цепи передается во вторичную посредством магнитного поля. Если в первичной цепи под действием напряжения источника возникает переменный ток, то во вторичной цепи за счет магнитной связи катушек индуцируется ЭДС, вызывающая протекание тока в нагрузке.

По второму закону Кирхгофа для первичной и вторичной цепей трансформатора можно записать

;.

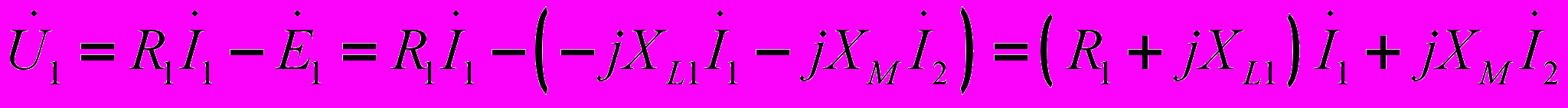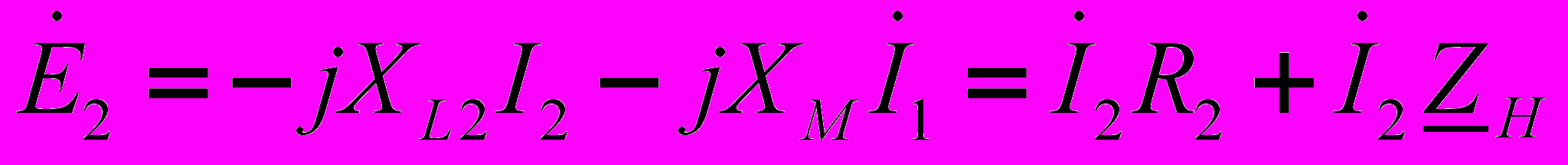Таким образом, уравнения воздушного трансформатора имеют вид: 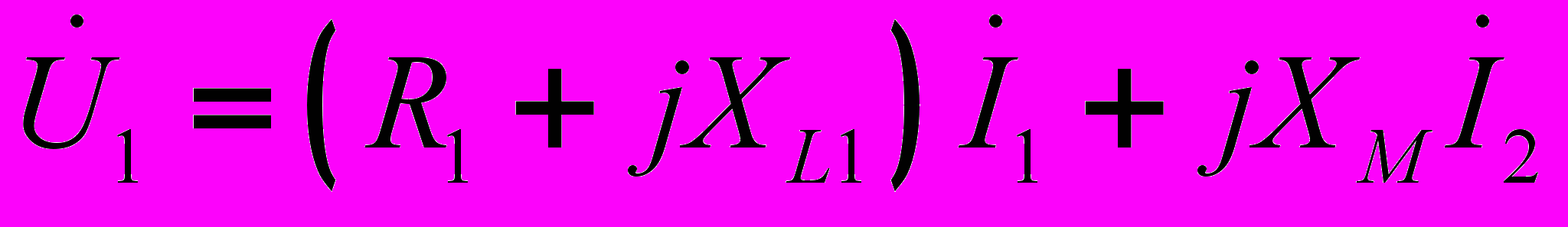(13)

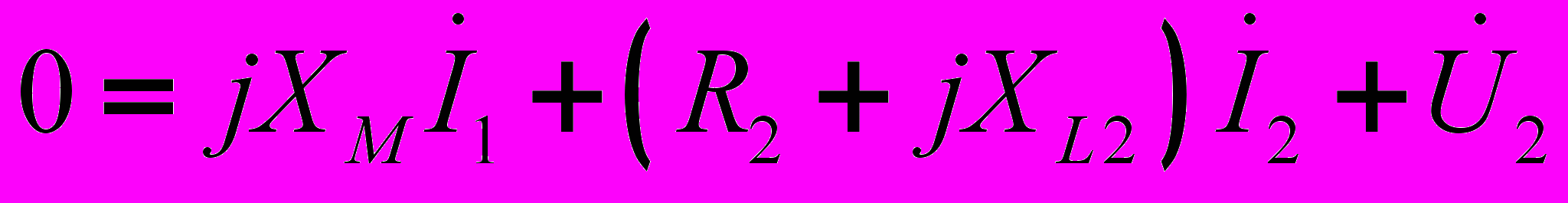.(14), где R₁ и R₂ - активные сопротивления обмоток; .

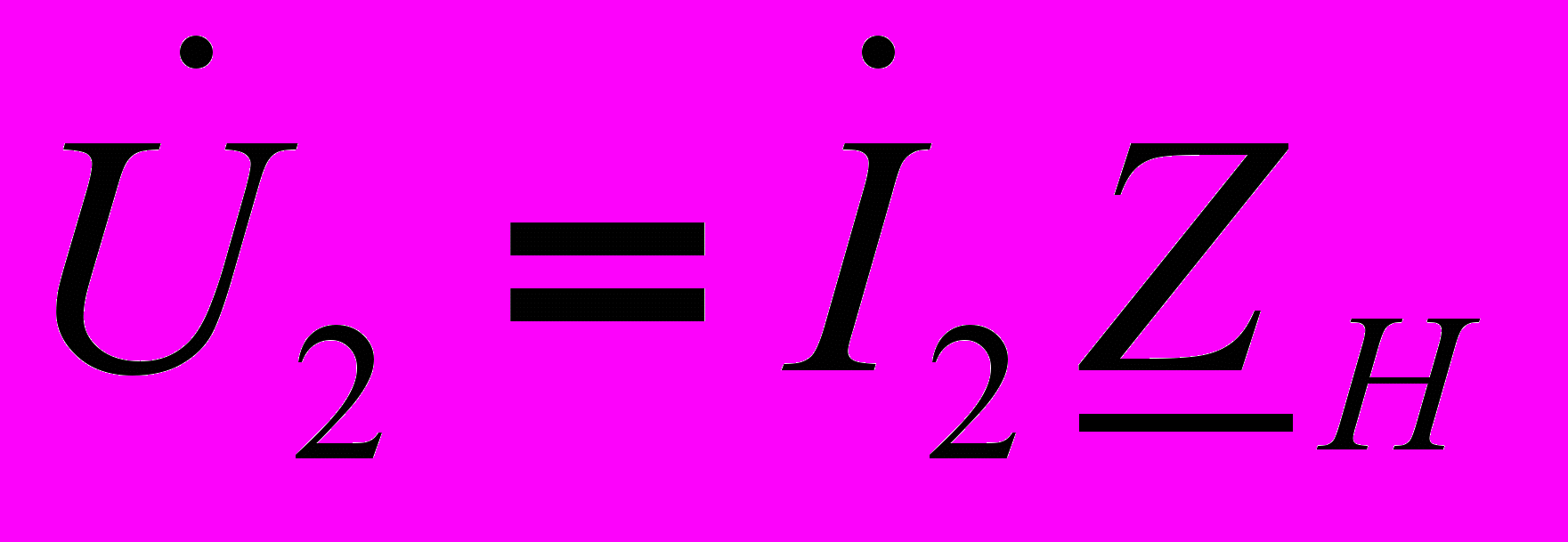Если уравнения (13) и (14) решить относительно 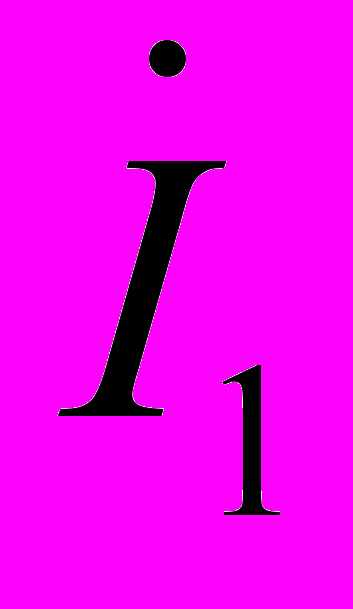, предварительно подставив в (14)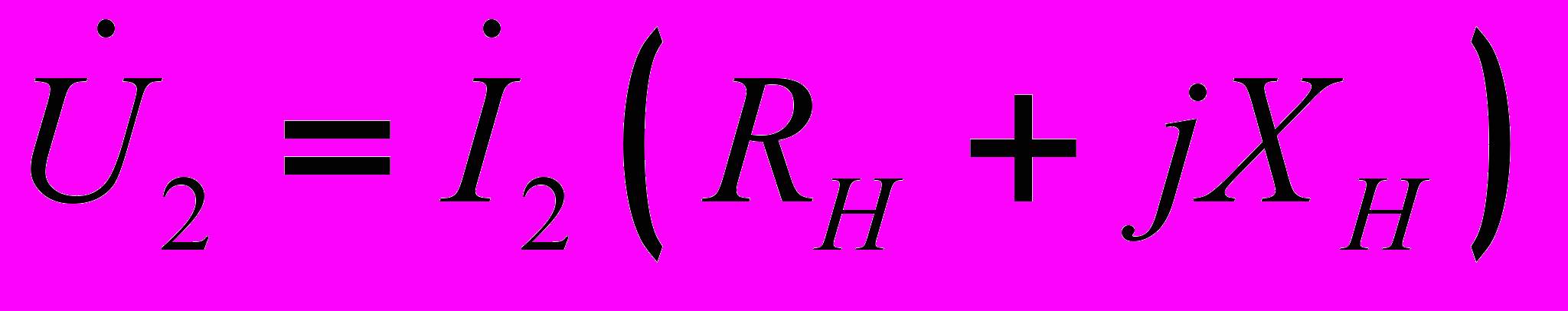

и обозначив 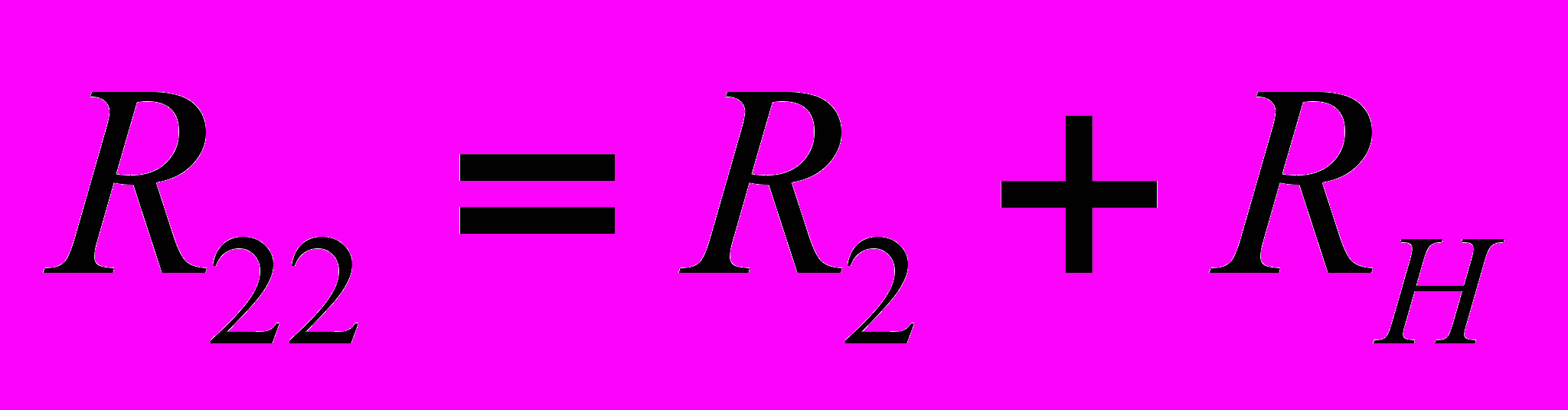; 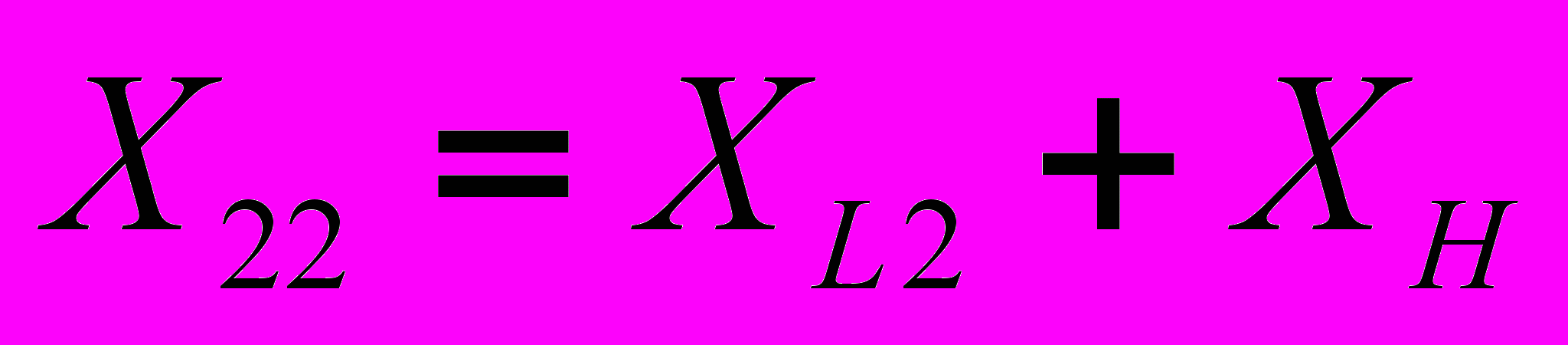, то получим 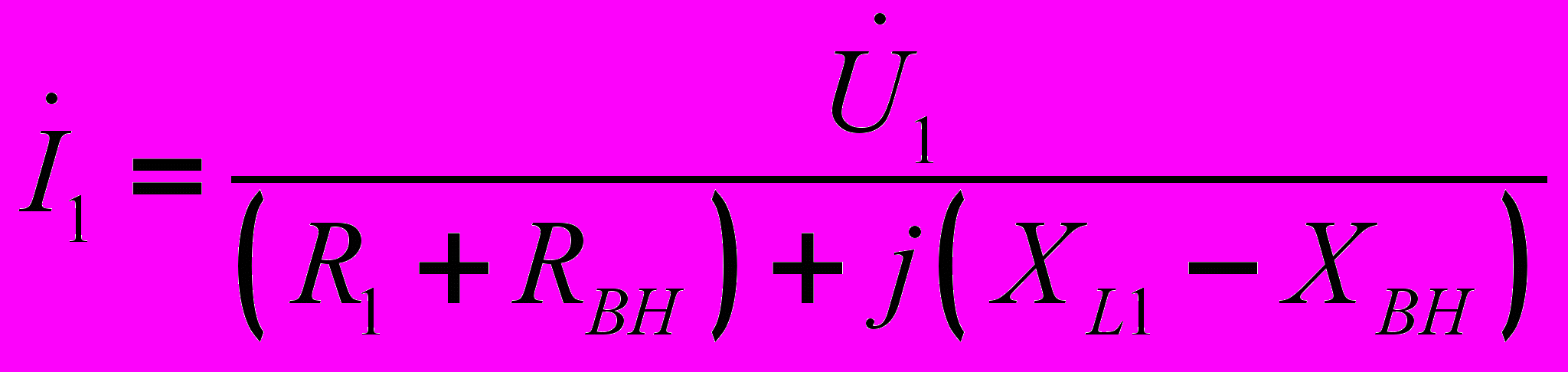(13), где 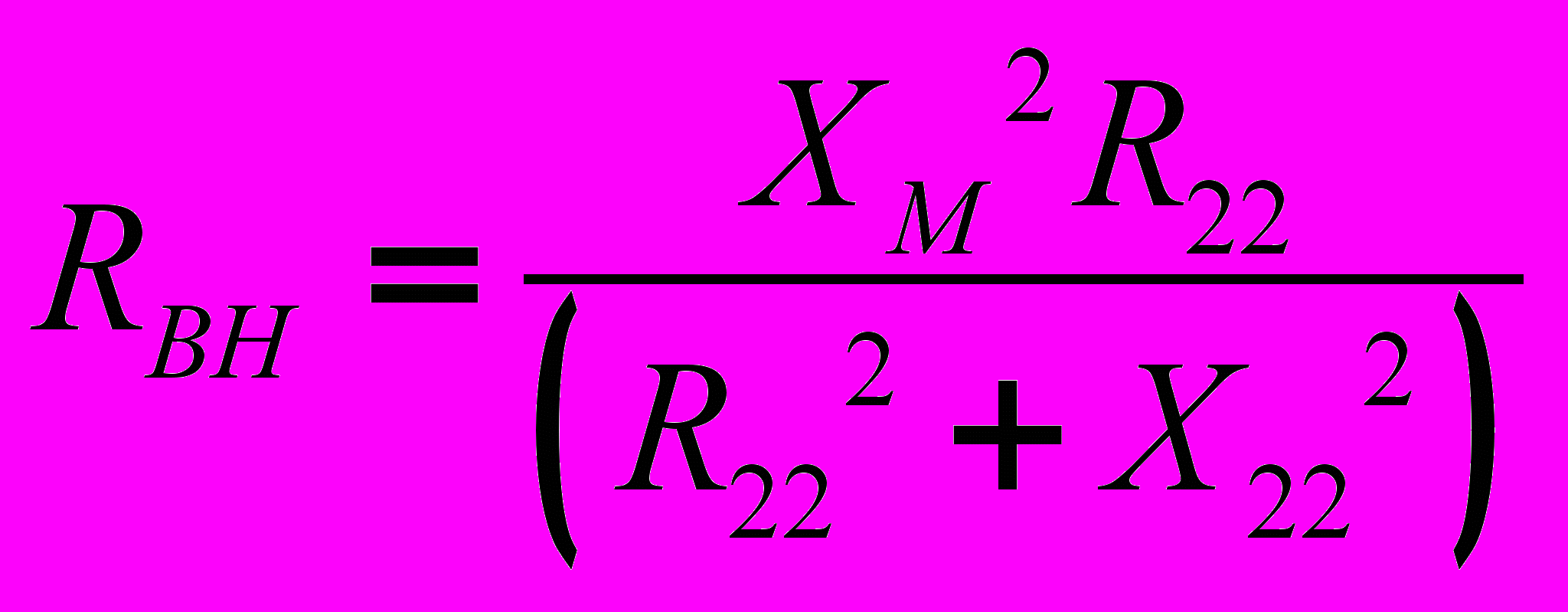;  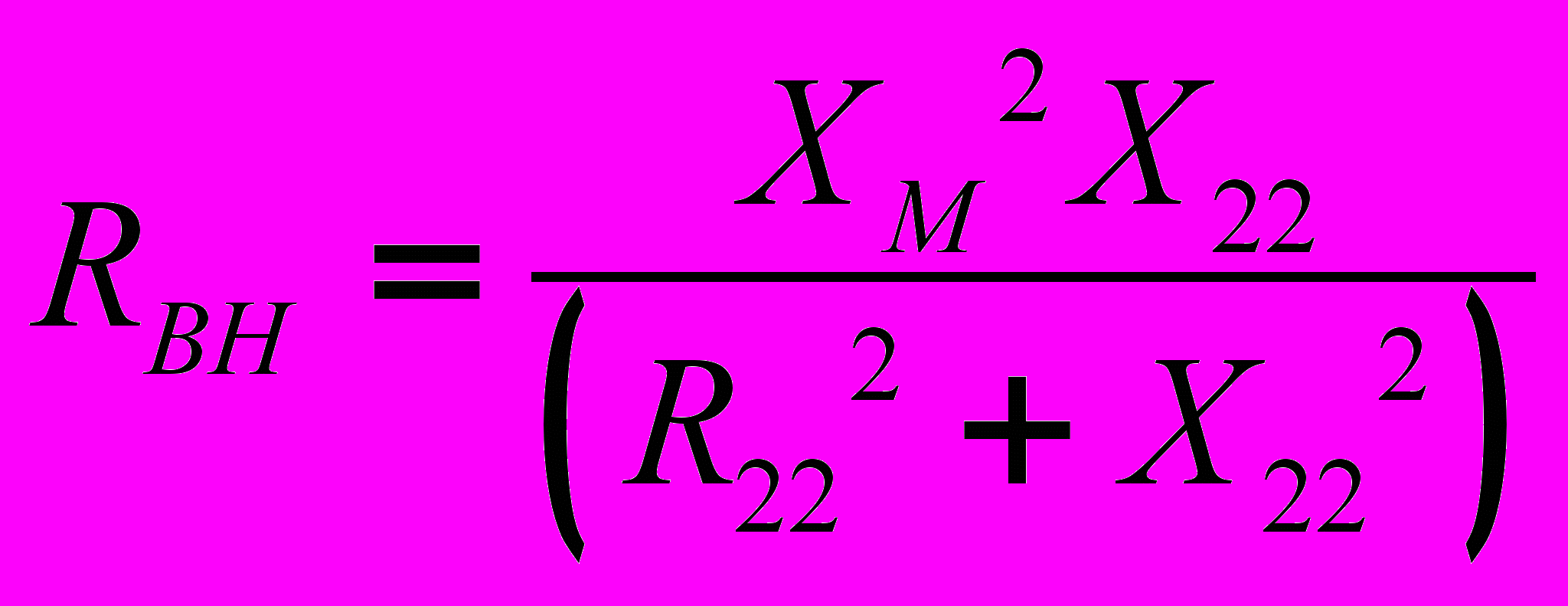- вносимые активное и реактивное сопротивления.

Таким образом, согласно (15) воздушный трансформатор со стороны первичной обмотки может рассматриваться как двухполюсник с сопротивлением .

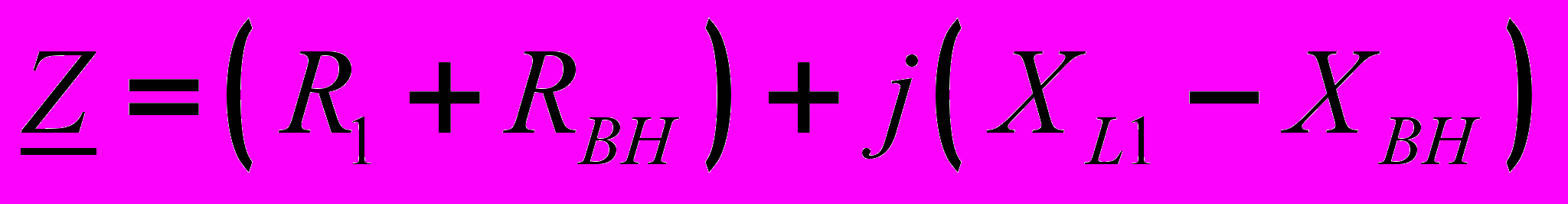Б
Рис.7.
аланс мощностей в цепях с индуктивно связанными элементами

Пусть имеем схему по рис. 7, где А – некоторый активный четырехполюсник. Для данной цепи можно записать , .

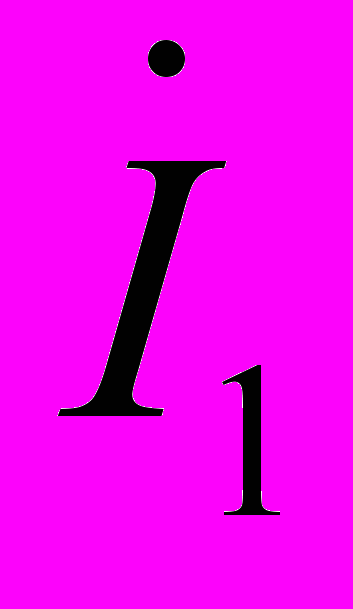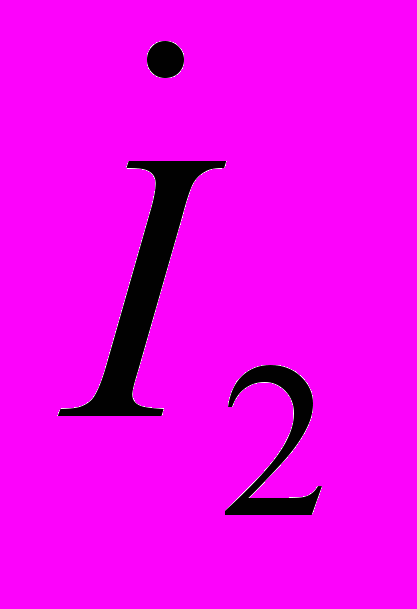Обозначим токи и  как: ; .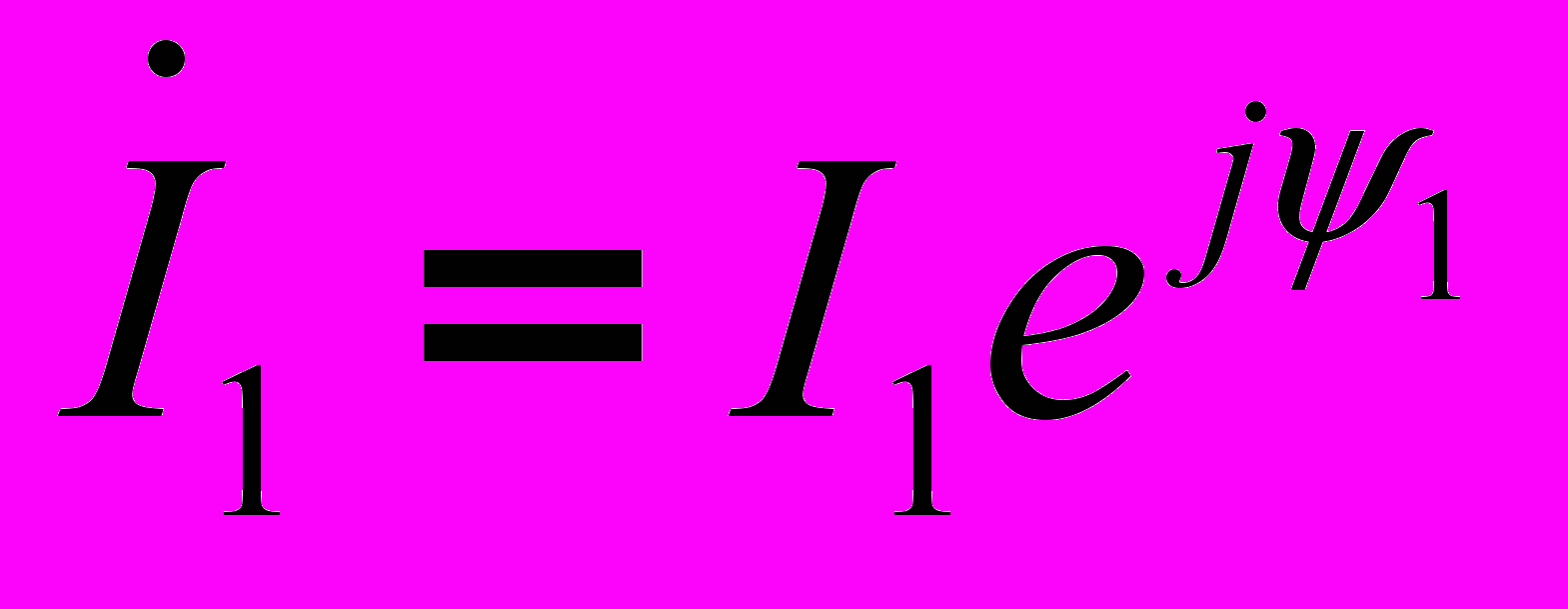

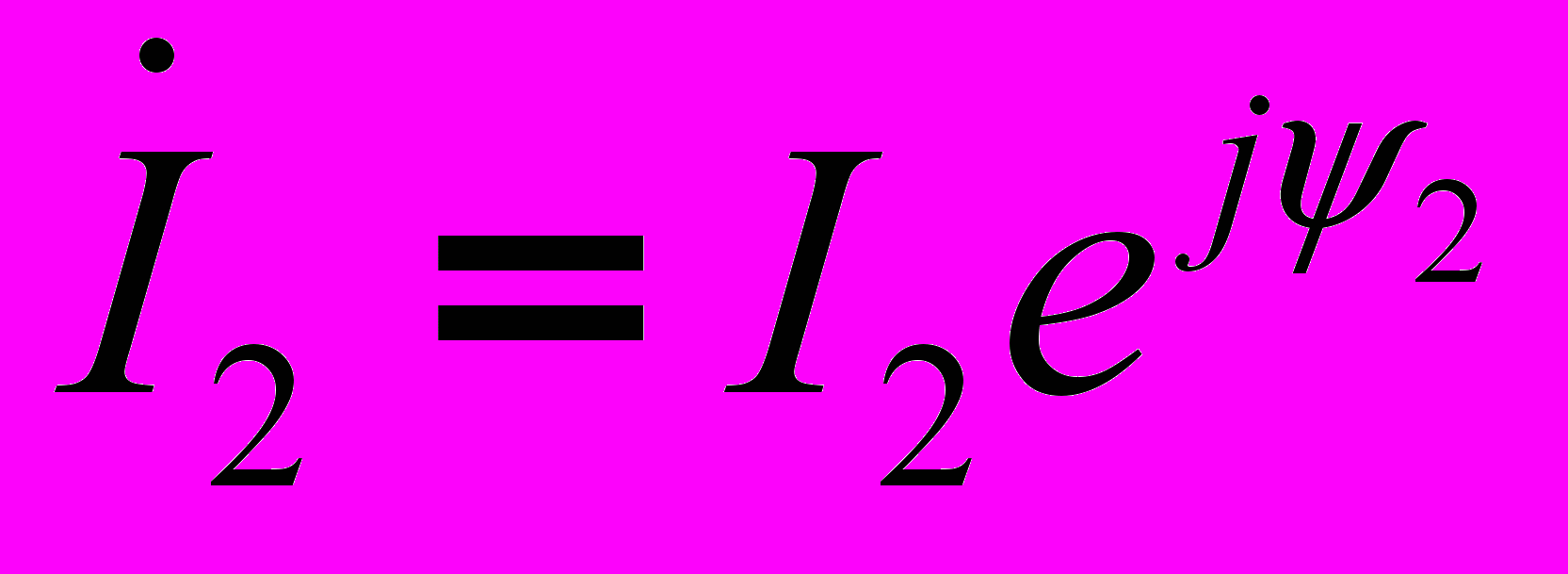Тогда для комплексов полных мощностей первой и второй ветвей соответственно можно записать:

;

.

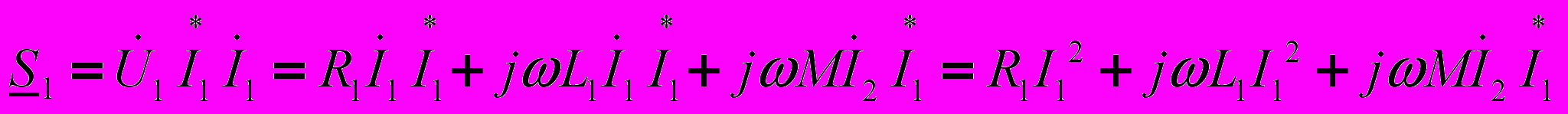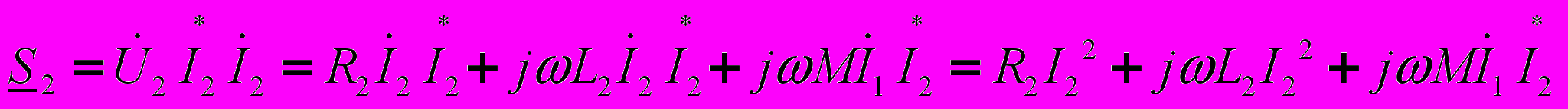Рассмотрим в этих уравнениях члены со взаимной индуктивностью:

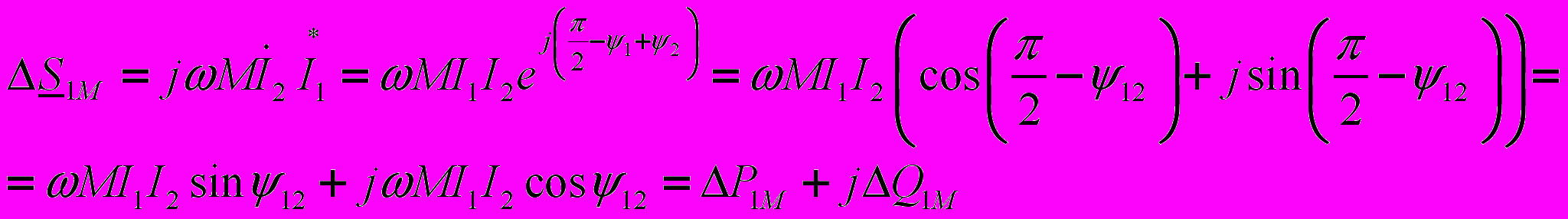(16)

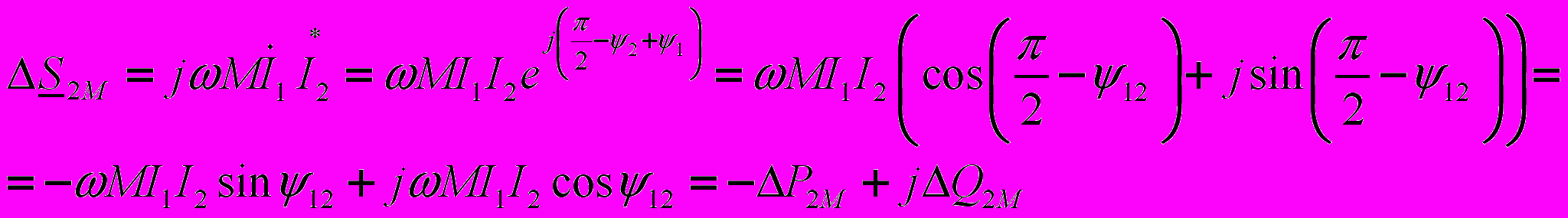(17).

где .

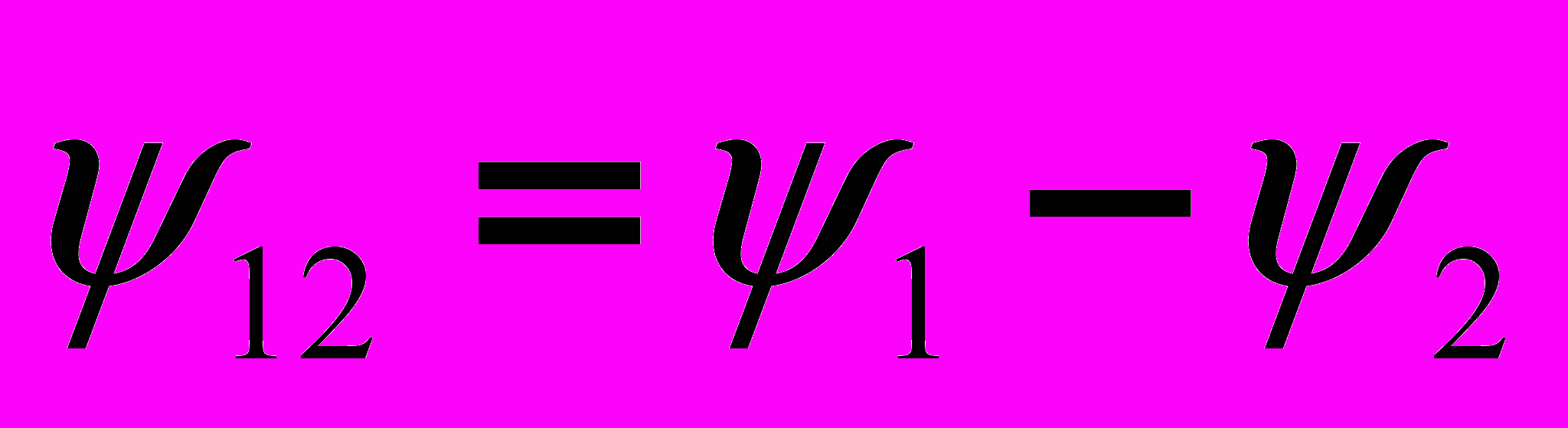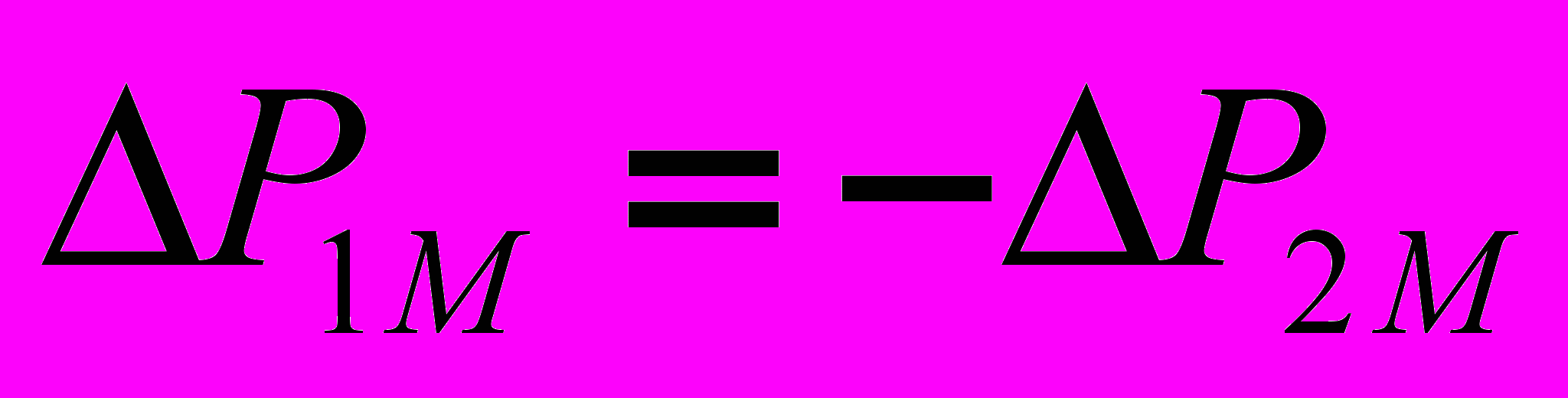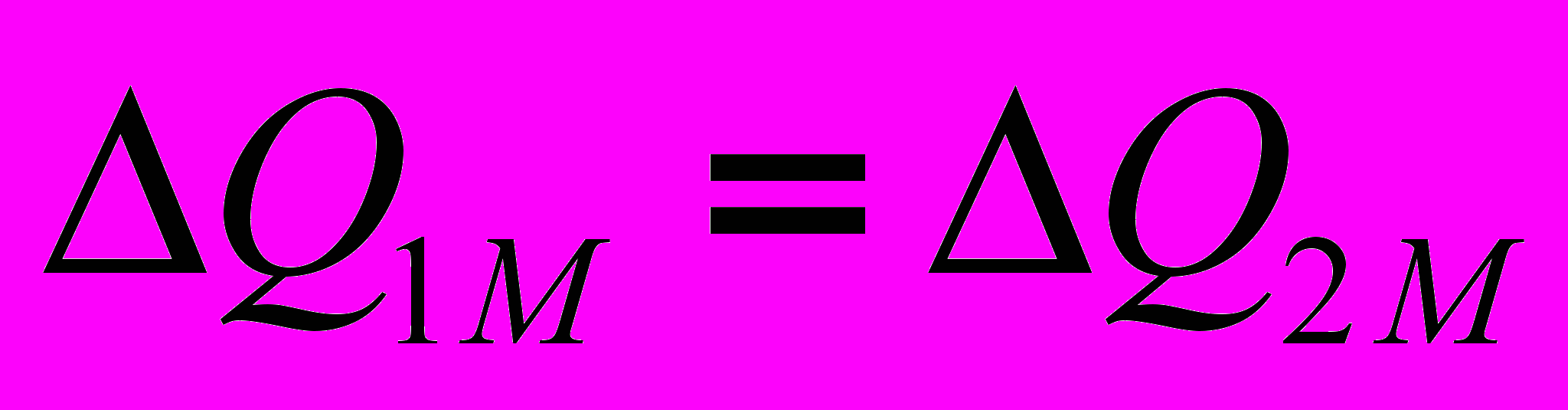Из (16) и (17) вытекает, что (18); (19)

Соотношение (18) показывает, что активная мощность передается от первой катушки ко второй. При этом суммарная активная мощность, обусловленная взаимной индукцией, равна нулю, т.к. 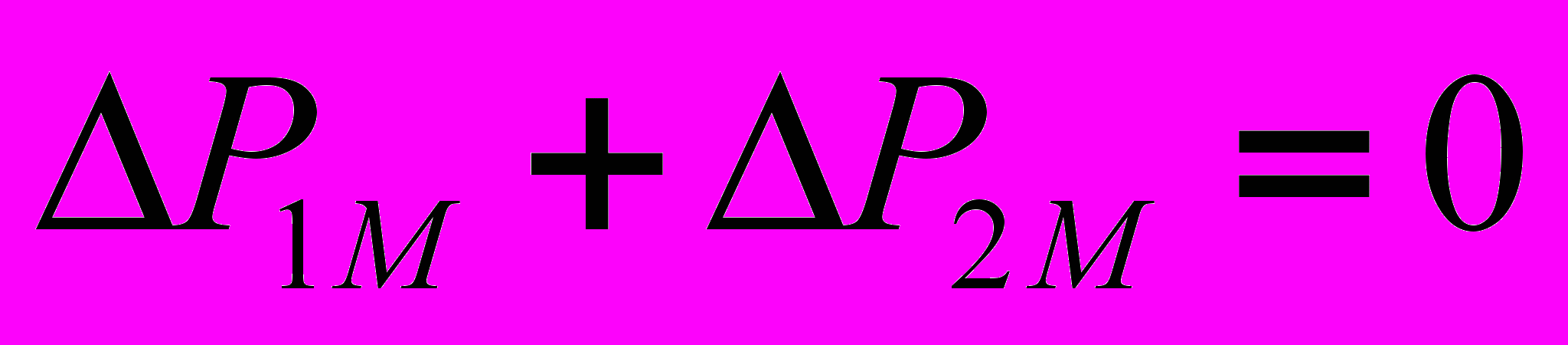. Это означает, что на общий баланс активной мощности цепи индуктивно связанные элементы не влияют.

Суммарная реактивная мощность, обусловленная взаимоиндукцией, равна

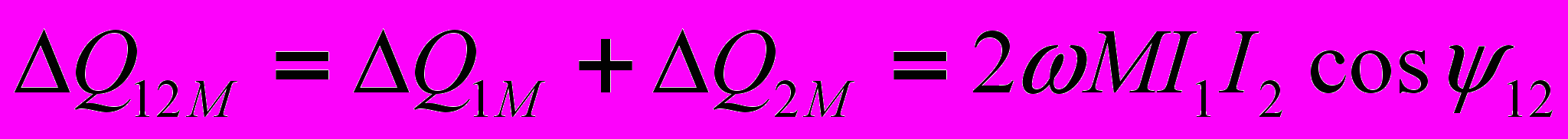
Таким образом, общее уравнение баланса мощностей с учетом индуктивно связанных элементов имеет вид

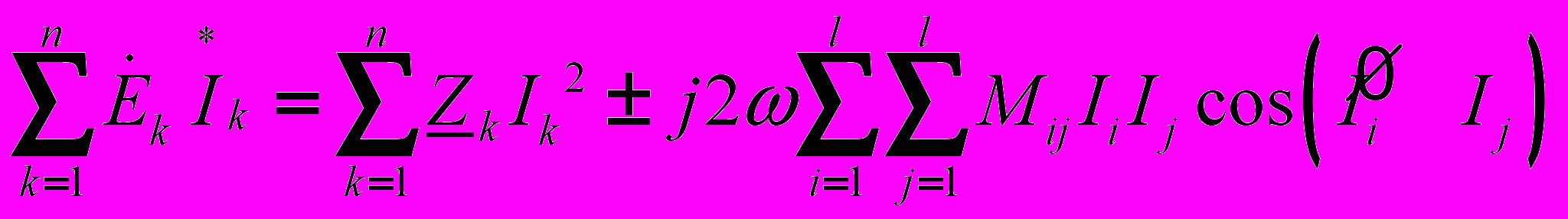(18),


где знак “+”  ставится при согласном включении катушек, а “-” – при встречном. Расчет разветвленных цепей при наличии взаимной индуктивности может быть осуществлен путем составления уравнений по законам Кирхгофа или методом контурных токов. Непосредственное применение метода узловых потенциалов для расчета таких цепей неприемлемо, поскольку в этом случае ток в ветви зависит также от токов других ветвей, которые наводят ЭДС взаимной индукции.