Расчет сложных цепей постоянного тока

Идея баланса мощностей (БМ) основана на законе сохранения энергии. В приложении к электрическим цепям он утверждает, что скорость потребления энергии (мощность) нагрузкой (сопротивлением) электрической цепи, равна скорости вырабатывания энергии источниками в её составе.

Формально БМ можно записать в виде:

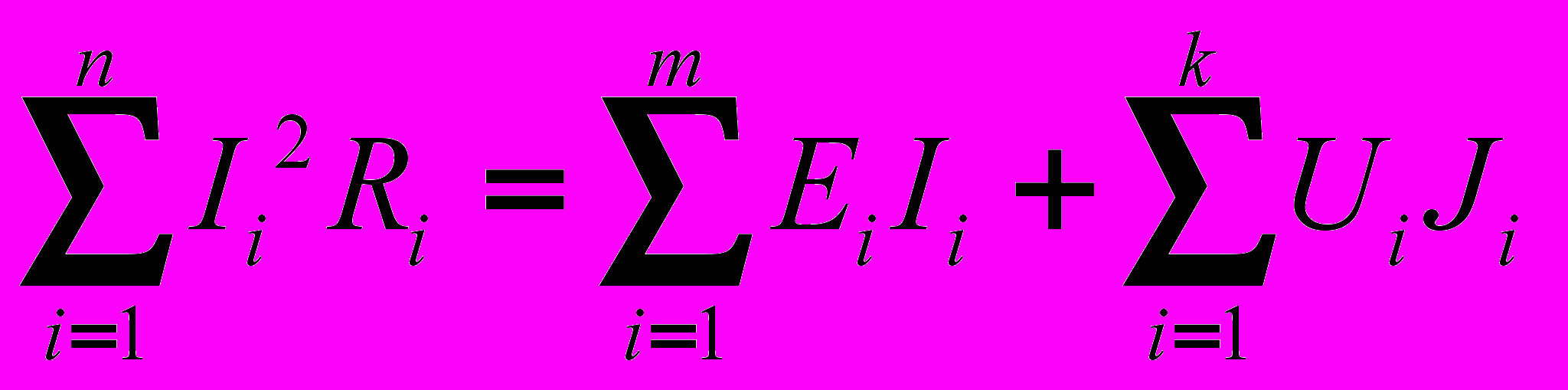, (1)

где - арифметическая сумма мощностей, потребляемых нагрузкой R_i.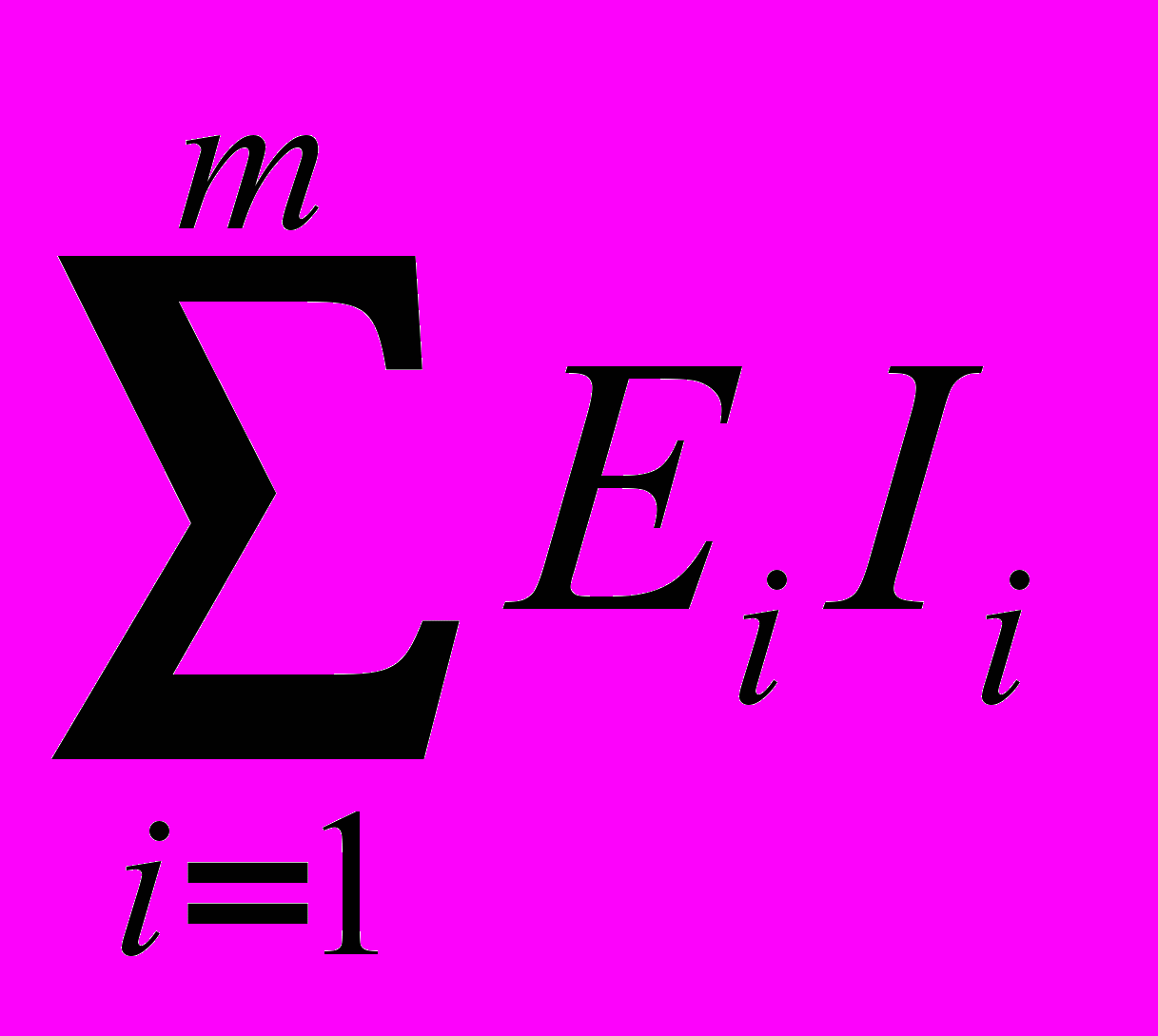

- алгебраическая сумма мощностей вырабатываемых источниками ЭДС. При этом слагаемое берется со знаком «+», если направление тока и ЭДС совпадают по направлению и со знаком «-», если не совпадают. В случае, если слагаемое отрицательное, то источник находится в схеме в режиме потребителя (например, заряд батареи).

- алгебраическая сумма мощностей вырабатываемых источниками тока.

В процессе расчета электрических цепей БМ обычно используют для проверки правильности найденного решения. Невыполнение БМ при расчете может только говорить об ошибке в расчетах. При несовпадении БМ в эксперименте говорит о неучтенных потерях в цепи.

Пример.



Определить токи в цепи и проверить правильность решения через баланс мощностей.

Решение.

Произведя расчет представленной цепи методом узловых потенциалов были получены следующие значения токов:



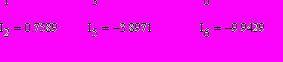
Определим мощности, потребляемые нагрузкой P_пр и источниками P_ист:



Подставим найденные токи:



По результатам расчетов можно видеть, что БМ выполняется.

Метод наложения.

Метод наложения (МН) основан на одном из основных принципов линейных систем – принципе наложения. МН может быть использован при расчете линейных эл. цепей, содержащих два и более источников энергии. Принцип наложения применительно к электрическим цепям заключается в следующем: ток в k – й ветви линейной электрической цепи равен алгебраической сумме токов, вызываемых каждым из источников в отдельности. Аналитически принцип наложения для цепи, содержащей n источников ЭДС и m источников тока, выражается соотношением

   (2)

Здесь G_kn - комплекс входной проводимости k – й ветви, численно равный отношению тока к ЭДС в этой ветви при равных нулю ЭДС в остальных ветвях; G_ki - комплекс взаимной  проводимости k – й и i– й ветвей, численно равный отношению тока в k – й ветви и ЭДС в i– й ветви при равных нулю ЭДС в остальных ветвях. Входные и взаимные проводимости можно определить экспериментально или аналитически, используя их указанную смысловую трактовку, при этом G_ki= G_ik, что непосредственно вытекает из свойства взаимности (см. ниже). Аналогично определяются коэффициенты передачи тока K_ki, которые в отличие от проводимостей являются величинами безразмерными.

При определении токов ветвей при помощи метода наложения следует поочередно оставлять в схеме по одному источнику, заменяя остальные их внутренними сопротивлениями, и рассчитать составляющие искомых токов в этих схемах. После этого полученные результаты для соответствующих ветвей суммируются – это и будут искомые токи в ветвях исходной цепи. В качестве примера использования метода наложения определим ток во второй ветви схемы на рис. 1,а.



Рис.1.

Принимая источники в цепи на рис. 1,а идеальными и учитывая, что у идеального источника ЭДС внутреннее сопротивление равно нулю, а у идеального источника тока – бесконечности, в соответствии с методом наложения приходим к расчетным схемам на рис. 1,б…1,г.

Принцип взаимности

Принцип взаимности основан на теореме взаимности, которую сформулируем без доказательства: для линейной цепи ток I_k в k – й ветви, вызванной единственной в схеме ЭДС E_i, находящейся в i – й ветви,

I_k=G_kiE_i будет равен току I_i в i – й ветви, вызванному ЭДС E_k, численно равной ЭДС E_i, находящейся в  k – й ветви, I_i=G_ikE_k. Отсюда в частности вытекает указанное выше соотношение G_ik=G_ki.

Иными словами, основанный на теореме взаимности принцип взаимности гласит: если ЭДС E, действуя в некоторой ветви схемы, не содержащей других источников, вызывает в другой ветви ток I (см. рис. 2,а), то принесенная в эту ветвь ЭДС E вызовет в первой ветви такой же ток I (см. рис. 2,б).



Рис.2.

Принцип компенсации

Принцип компенсации основан на теореме о компенсации, которая гласит: в любой электрической цепи без изменения токов в ее ветвях сопротивление в произвольной ветви можно заменить источником с ЭДС, численно равной падению напряжения на этом сопротивлении и действующей навстречу току в этой ветви. Для доказательства теоремы выделим из схемы произвольную ветвь с сопротивлением i, по которой протекает ток I, а всю остальную часть схемы условно обозначим некоторым активным двухполюсником А (см. рис. 3,а).



Рис.3.

При включении в ветвь с R двух одинаковых и действующих навстречу друг другу источников ЭДС с E=IR (рис. 3,б) режим работы цепи не изменится. Для этой цепи

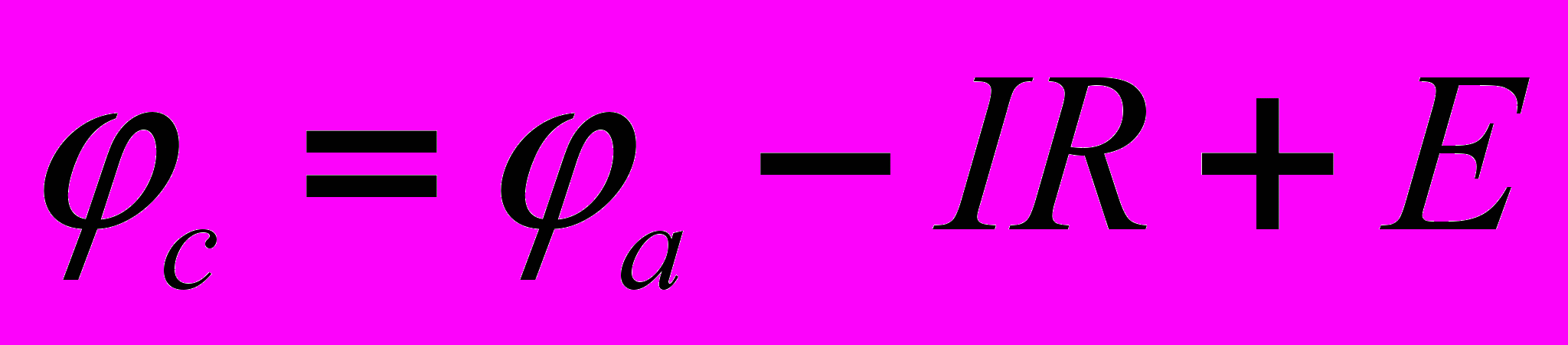(3)

Равенство (3) позволяет гальванически соединить точки а и c, то есть перейти к цепи на рис. 3,в. Таким образом, теорема доказана. В заключение следует отметить, что аналогично для упрощения расчетов любую ветвь с известным током i можно заменить источником тока J=I.