Прикладная информатика в экономике Бийск Издательство Алтайского государственного технического университета им. И. И. Ползунова 2008

Вид материала

Документы

Содержание 2.8 Представление в компьютере целых и дробных чисел

Подобный материал:

• Бийск Издательство Алтайского государственного технического университета им., 1773.05kb.
• Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 1610.7kb.
• Конкурс организует Общественная организация «нива» при участии Институт экономики, 61.02kb.
• Самостоятельная работа студентов методические рекомендации по выполнению самостоятельной, 922.35kb.
• Самостоятельная работа студентов методические рекомендации по дисциплине сд., 302.18kb.
• Учебно-методический комплекс для студентов заочного обучения специальности Прикладная, 81.9kb.
• «Финансы и кредит», 649.21kb.
• Учебно-методическим советом экономического факультета мировые информационные ресурсы, 221.33kb.
• Реклама как мифологическая коммуникативная система, 395.36kb.
• Лабораторный комплекс на основе внутрисхемного эмулятора микроконтроллеров стандарта, 78.16kb.

2.8 Представление в компьютере целых и дробных чисел

Одним битом, как уже упоминалось, могут быть выражены два понятия: 0 или 1. Если количество битов увеличить до двух, то уже можно выразить четыре различных понятия: 00, 01, 10, 11. Тремя битами можно закодировать восемь различных значений: 000, 001, 010, 011, 100, 101, 110, 111. Увеличивая на единицу количество разрядов в системе двоичного кодирования, увеличиваем в два раза количество значений, которое может быть выражено в данной системе, то есть общая формула имеет вид:

,

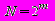где N – количество независимых кодируемых значений;

m – разрядность двоичного кодирования, принятая в данной системе.

Используя двоичную систему счисления, компьютер в одном байте может хранить любое целое число в диапазоне от 0 до 255 (от 00000000 до 11111111), а в двух байтах от 0 до 65535.

В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код. Последние две формы применяются особенно широко.

Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково  двоичными кодами с цифрой 0 в знаковом разряде. Например:

Десятичное число	1	2	3
Двоичное представление	001	010	011

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.

1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа  двоичный код его абсолютной величины. Например:

Десятичное число	–1	–2	–3
Двоичное представление	101	110	111

2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы  нулями. Например:

Десятичное число	–1	–2	–3
Двоичное представление	110	101	100

3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Например:

Десятичное число	–1	–2	–3
Двоичное представление	111	110	101

Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.

Числа, имеющие дробную часть, также называют вещественными. В большинстве программных систем при их написании вместо запятой принято писать точку. Так, например, число 5 – целое, а числа 5.1 и 5.0 – вещественные.

Для кодирования вещественных чисел используется 80-разрядное кодирование. При этом число предварительно преобразуют в форму представления чисел с плавающей точкой или нормализованную форму. В нормальной форме число представляется в виде произведения

X = mq ^p,

где m – мантисса числа;

q – основание системы счисления;

p – порядок.

Например, для числа 3,1415926 = 0,31415926  10¹ мантисса равна 0,31415926, а порядок равен 1. Для задания числа в нормальной форме требуется задать знаки мантиссы и порядка, их модули в q-ичном коде, а также основание системы счисления. Нормальная форма представления чисел неоднозначна, ибо взаимное изменений m и p приводит к плаванию точки (запятой). Например, десятичное число 73,28 в нормальной форме может быть записано в следующих вариантах:

73,28 = 73,28 10⁰ = 7,328  10¹ = 0,7328 10² = 0,07328  10³ = …

Количество цифр в целой и дробной частях мантиссы и в порядке может быть любым. На знак числа и знак порядка требуется 2 бита. Если остальные 6 бит байта отдать под порядок (2⁴ = 64), то получается достаточно большой диапазон по порядкам. При однобайтном порядке диапазон изменения чисел составляет от 2^-128 до 2¹²⁷ или приблизительно от 10^-38 до 10³⁸. Для большинства случаев этого бывает достаточно, так как на практике точность измерений обычно не превышает 10^-8. Что касается мантиссы, то можно заметить, что чаще всего используются числа со сравнительно короткой мантиссой от 3 до 5 десятичных цифр и довольно редко – с мантиссами от 10 до 15 цифр. Для записи мантиссы берут 3 байта, при этом точность составляет 2²⁴ или 10⁸. Таким образом, получается 4 байта вместе с байтом знаков и порядка, что согласуется с размером ячейки для длинных целых чисел. Действительные числа с длинной мантиссой до 15 значащих цифр обеспечиваются удвоением количества байтов, отводимых под число, причем 4 дополнительных байта отдаются целиком мантиссе. Этим способом достигается так называемая двойная точность вычислений.

Для хранения дробных чисел в памяти компьютера требуется запоминание не только нулей и единиц, образующих двоичное представление числа, но и запоминание позиции разделителя (десятичной точки), отделяющего целую часть от дробной.

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа.