Geum.ru

В.І. Склабінський (Вступ, розіл 4, висновки) доцент кафедри «Процеси та обладнання хімічних І нафтопереробних виробництв»

Вид материалаДокументы

Содержание


2.3 Дослідження впливу конструкції газорозподільної решітки
2.4 Дослідження впливу порозності шару
2.5 Дослідження різних методик розрахунку апаратів псевдозрідженого шару
2.5.1 Виведення залежності для розрахунку критерія Архимеда і програми для його розрахунку
2.5.2 Вибір оптимального метода розрахунку швидкості теплоносія
Висновки по главі
Подобный материал:
1   2   3   4   5

2.3 Дослідження впливу конструкції газорозподільної решітки


Механізм утворення псевдозрідженого шару в апараті можливо представити таким чином. При подачі через розподільну решітку знизу догори газового потоку з невеликою швидкістю шар ретура залишається нерухомим. Якщо поступово збільшувати швидкість газу до значення, при якому вага зернистого матеріалу у шарі урівноважується силою гідродинамічного тиску висхідного потіку, тверді частки перебувають у гідродинамічній рівновазі, тобто шар стає текучим і набуває деякі інші властивості крапельної рідини. При подальшому збільшенні швидкості газу шар розсширюється, інтенсивність руху часчток збільшується, але без порушення гідродинамічної рівноваги. При досягненні швидкості газу, при якій сили гідродинамічного тиску стають більше сил тяжіння, частки виносяться з шару. Швидкість газу, при якій нерухомий шар зернистого матеріалу переходить у псевдозріджений стан, називається швидкістю початку псевдозрідження (або першою критичною). Швидкість газу, при якій тверді частки виносяться з шару, називається швидкістю виносу (або другою критичною). Таким чином, діапазон псевдозрідження обмежений першою і другою критичними швидкостями. Якщо швидкість газу ненабагато перевищує швидкість початку псевдозрідження, то рух часток вражений слабо – шар знаходиться у стані спокійного псевдозрідження. Із збільшенням швидкості газу в шарі починають з'являтися невеликі міхури, які підвищують інтенсивність перемішування часток. Вільна поверхня шару при цьому обкреслена досить різко, сприймаючи порівняно невеликі коливання. Такий шар отримав назву власне киплячого шару. При подальшому збільшенні швидкості газу зростає розмір міхурів. Останні, піднімаючись зазвичай з більшою швидкістю, ніж інша частина газу, різко турбулізують систему. В цьому випадку кажуть про шар з барботожем міхурів. Вільна поверхня такого шару сприймає значні коливання; міхури, що виходять з шару, проривають цю поверхню, утворюючи над нею сплески матеріалу. Остаточно, подальше збільшення швидкості газу прозводить до повного размивання вільної поверхні шару і виносу твердих часток.

Необхідно відмітити, що на характеристики псевдозрідженого шару значний вплив оказує конструкція газорозподільної решітки [14].

Найбільш широко застосовуються газорозподільні решітки у вигляді простої перфорованої плити, плити з отворами, прикритими ковпачками або конусами.

На рис.2 показаний вплив конструкції розподільного пристрою на характеристику киплячого шару.



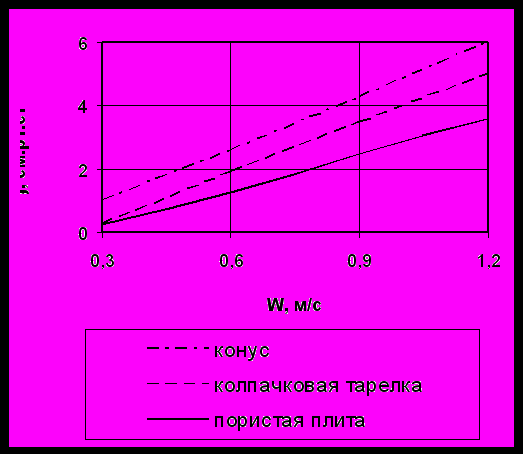
Рисунок 2 – Флуктуації тиску Fg у псевдозрідженому шарі з різними розподільними пристроями


З рис.2 видно, що у діапазоні критичних швидкостей початку псевдозрідження перепади тиску при використанні розподільних тарілок з ковпачками будуть на 29%, а з конусами – на 41% більше, ніж при використанні перфорованих решіток (пористих плит). Зниження флуктуацій тиску призводить до стабілізації зрідженого шару, зменшення гідравлічного опору, зниження витрат на створення і підтримання псевдозрідженого шару. Також слід відмітити, що пористі решітки дають найбільш однорідний шар, забезпечуають наібільший ступінь його розширення, мають просту конструкцію, дешеві у виготовленні і експлуатації. Тому в апаратах псевдозрідженого шару рекомендується використовувати перфоровані решітки.


2.4 Дослідження впливу порозності шару


Також однією з основних характеристик псевдозрідженого шару є порозность шару ε (доля пустот, відносний вільний об'єм). На рис.3 представлена залежність порозности шару від співвідношення діаметру часток до діаметру апарату для часток різної форми і фракції [14].



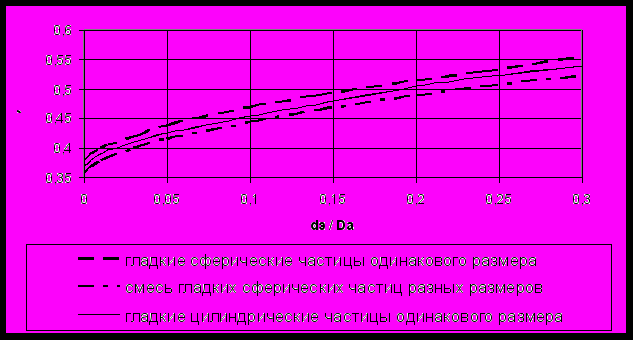
Рисунок 3 – Порозность ε0 шару різних матеріалів у трубах з насадкою при різних відношеннях dэ/Da


З рис.3 видно, що значення порозности шару залежить:

- від форми часток: чим ближче вона до сферичної, тим менше порозность;

- від гранулометричного складу: чим ширше фракція зернистого матеріалу, тим менше порозность;

- від діаметру апарата: при зьільшенні співвідношення діаметру часток до діаметру апарату порозность шару збільшується.

Графіки, наведені на рис.3, дозволяють визначити орієнтовне значення діаметра проектуємого апарату. Для цього необхідно задатися критичним значенням порозності початку псевдозрідження і прийняти певну форму часток.

Критичне значення порозності початку псевдозрідження дорівнює 0,38-0,42. В апараті знаходиться суміш гладких сферичних часток різних розмірів. Виходячи з графіків на рис. 3 орієнтовний діаметр апарата складає 2 м.

Необхідно відмітити, що порозность нерухомого шару суттєво залежить від способу засипки матеріалу в апарат. Механічний вплив на шар (постукування по апарату, трамбування і т.і.) призводить до зменшення порозності; з іншого боку, достатньо інтенсивна вібрація може призвести до розрихлення шару [14].


2.5 Дослідження різних методик розрахунку апаратів псевдозрідженого шару


Для підтримання шару твердих часток у псевдозрідженому стані необхідний безперервний обмін енергією між ними і зріджуючим агентом [14]. Енергія, ща віддається зріджуючим агентом, витрачається на подолання тертя часток одне до одного і газу об їх поверхню, на зміну кінетичної енергії газу і розширення шару, а також на тертя часток і газу о стінки апарату. Перелічені складові сумарної енергії не рівноцінні: найбільшими є витрати енергії на подолпння тертя газу о поверхню часток. Сумарні витрати енергії в одиницю часу складають:


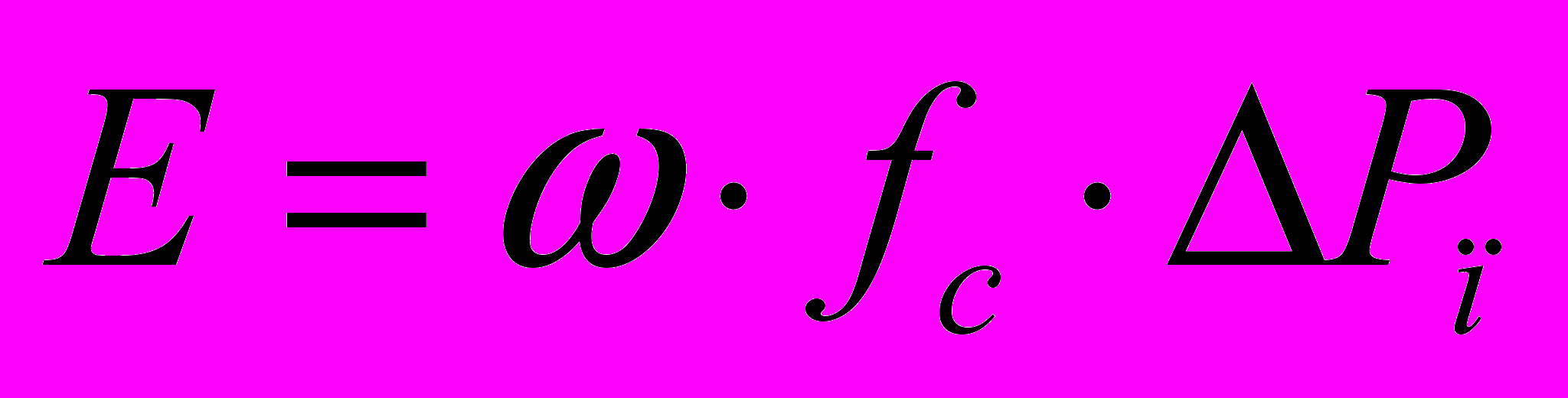(1)


де 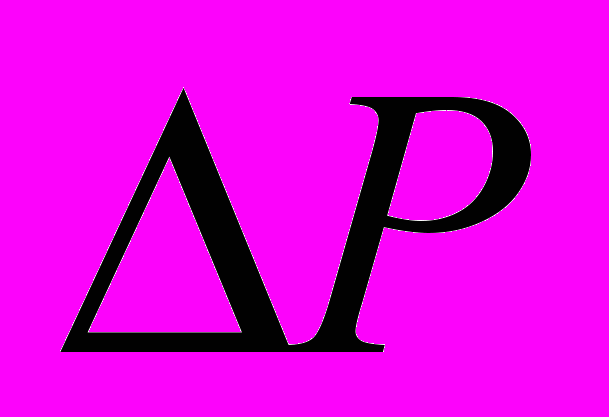- перепад тиску при русі газу (рідини) через псевдозріджений шар, тобто гідравлічний опір шару;

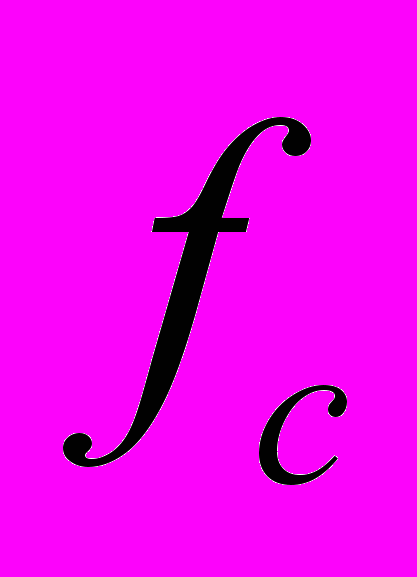- площа поперечного перетину шару;

- швидкість зріджуючого агента.

Значення 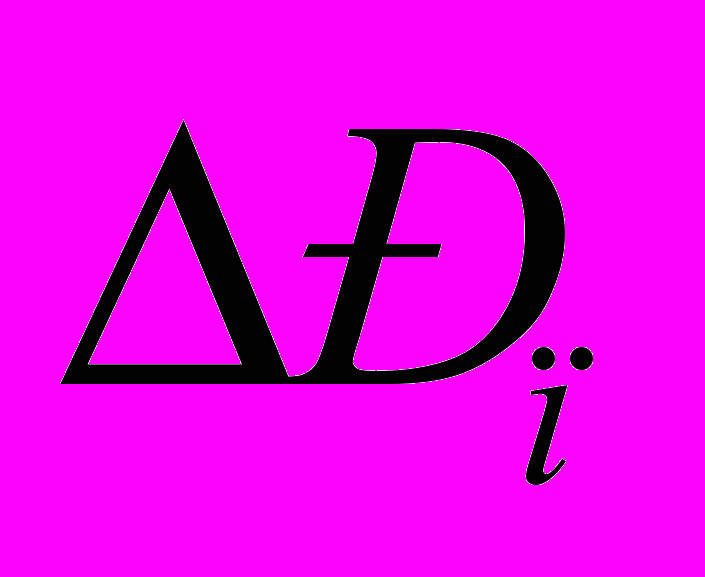, знання якого необхідно при виборі машин для подачи зріджуючого агента в систему завислого шару, також є однією з основних характеристик, впливаючих на вибір технологічних параметрів і конструктивних особливостей апаратурного оформлення. Так, наприклад, при зниженні гідравлічного опору завислого шару знижуються енергетичні витрати на його створення і підтримання стабільного стану.

В техниці псевдозрідження велике значення мають дослідження граничних режимів – умов переходу шару сипкого матеріалу при продуванні його газом від нерухомого стану до псевдозрідженого. Важливо також визначити область стійкої роботи апарату.

Типова крива залежності гідравлічного опору ΔР конічного і циліндроконічеського шарів від швидкості потоку газу ω приведена на рис .4 [14].




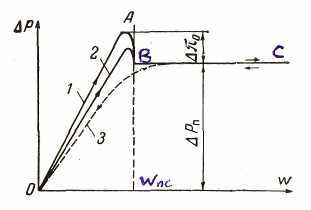
Рисунок 4 – Реальні криві псевдозрідження:

1 – при щільній упаковці часток у нерухомому шарі; 2 – при рихлій упаковці часток; 3 – крива зворотнього ходу


Насамперед реальна крива псевдозрідження характеризується наявністю пику тиску в момент переходу шара у псевдозріджений стан, що пояснюється необхідністю додаткової витрати енергії на подолання сил зчеплення часток. Висхідна гілка ОА в реальних умовах, як правило, не відтворюється, оскільки перепад тиску в нерухомому шарі залежить від щільності первинної упаковки часток. В утрамбованому шарі гілка ОА піднімається крутіше (лінія 1), ніж при більш рихлій упаковці (лінія 2). Величина піку тиску в першому випадку більша, ніж в другому.

Реальна крива псевдозрідження виявляє гістерезис: так звані лінії прямого і зворотного ходу (отримані відповідно при поступовому збільшенні і поступовому зниженні швидкості газу) поблизу точки А не збігаються, причому на лінії зворотного ходу відсутній пік тиску.

Ділянку ВС характеризує режим розвиненого псевдозрідження, гідравлічний опір на цій ділянці постійний.

Гідравлічний опір в апаратах із змінним перетином можна розрахувати по формулі:

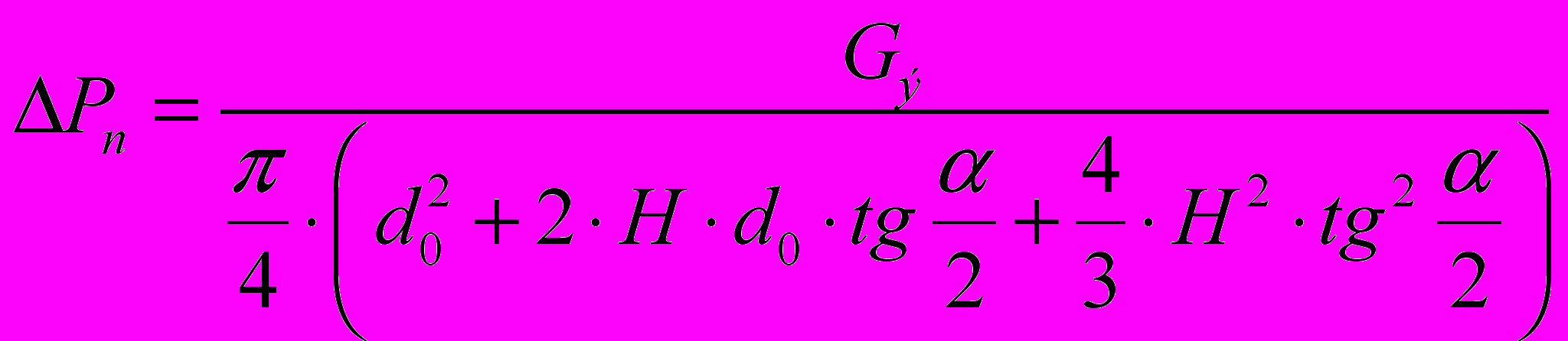(2)

де 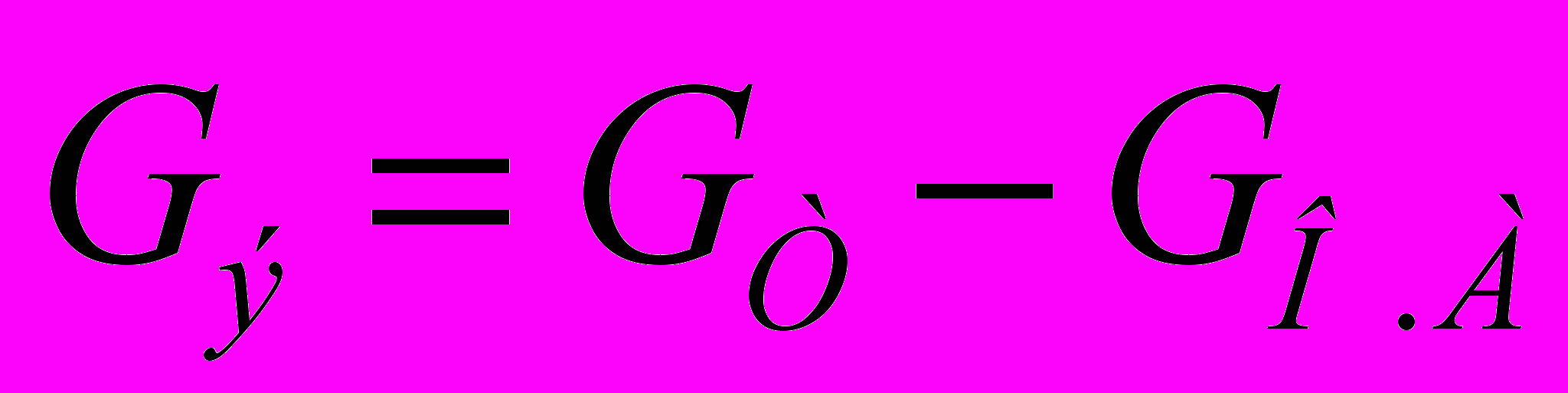- ефективна вага твердого матеріалу в шарі, яка дорівнює різниці у вазі твердих часток і зріджуючого агента в об’ємі цих часток;

- висота псевдозрідженого шару;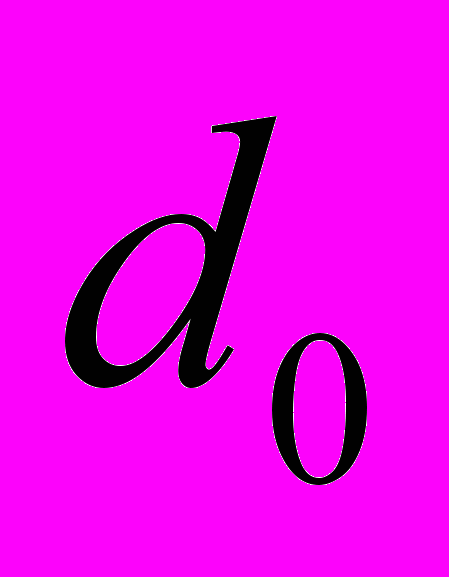

- діаметр решітки апарату;

- кут при вершині конуса апарату.


При виведенні рівняння (2) передбачалося [14], що псевдозрідження зернистого матеріалу відбувається по всьому поперечному перетину шару. Насправді ця умова не завжди витримується. Зокрема при псевдоожіженії в конічних і конічно-циліндрічних апаратах з кутом при вершині конуса 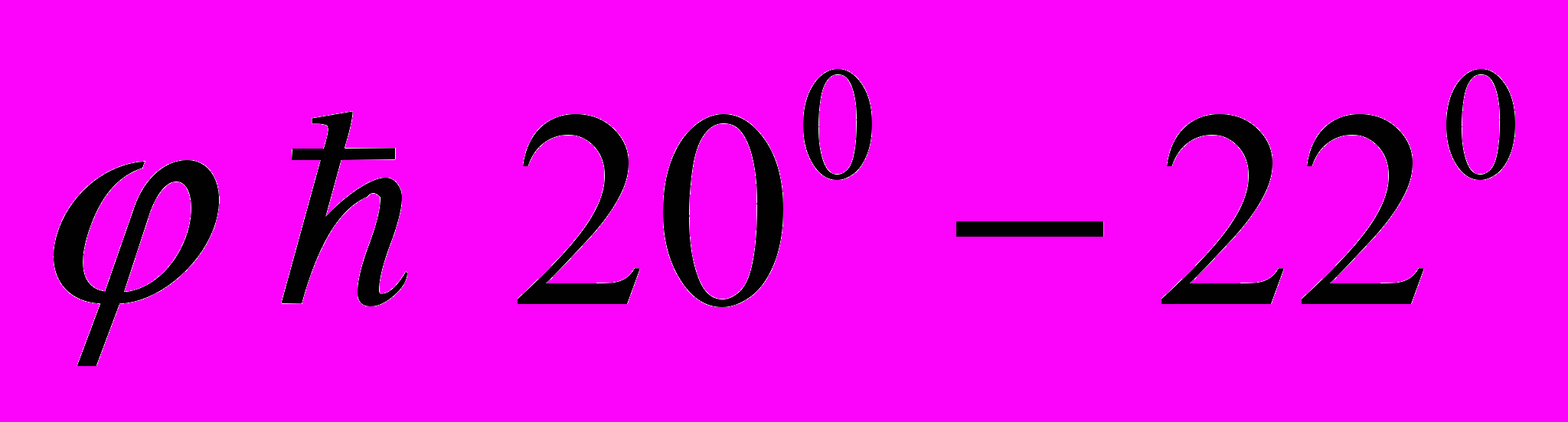шар буває зріджений не по всьому верхньому і проміжним перетинам. В цих апаратах виникає псевдозріджене ядро шару, діаметр верхнього перетину якого значно менше діаметру апарату в тому ж перетині.

На підставі візуальних спостережень [14] за поведінкою шару встановлено, що оптимальне значення кута розкриття конуса в апаратах конічною і циліндроконічеськой форми .

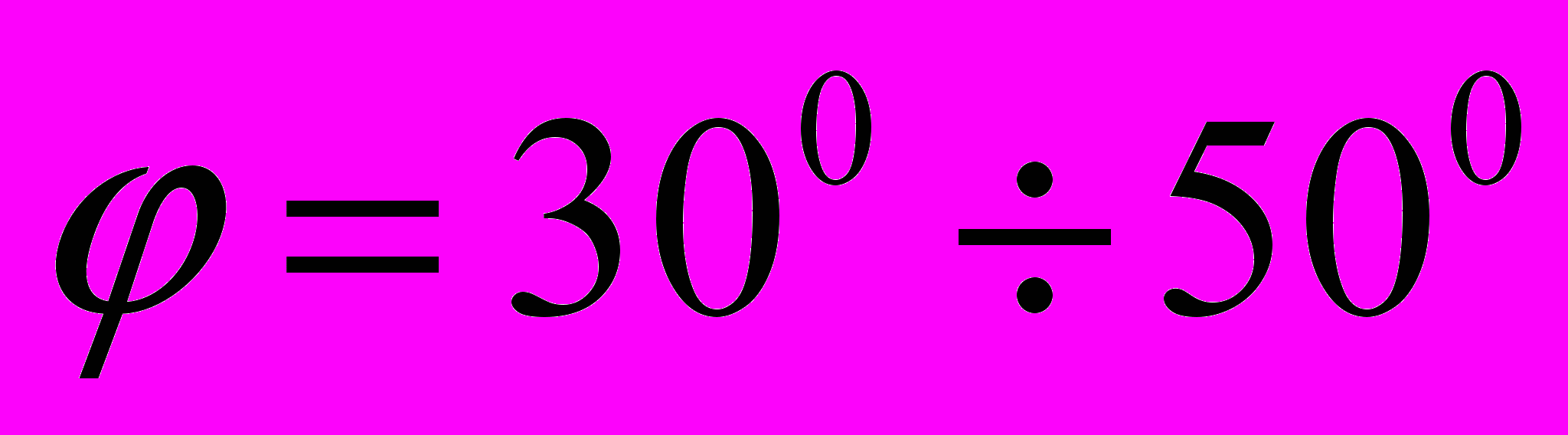З рис.4 видно, що перехід шару від нерухомого стану до псевдозрідженого відбувається при збільшенні швидкості газу до певного критичного значення (швидкості початка псевдозрідження). Ця швидкість залежить від висоти шару, фізичних характеристик матеріалу і газу, а також від геометричних параметрів апарату.


2.5.1 Виведення залежності для розрахунку критерія Архимеда і програми для його розрахунку


Для визначення критичної швидкості початку псевдозрідження часток і робочої швидкості руху теплоносія необхідно визначити критерій Архимеда, який розраховують по формулі:

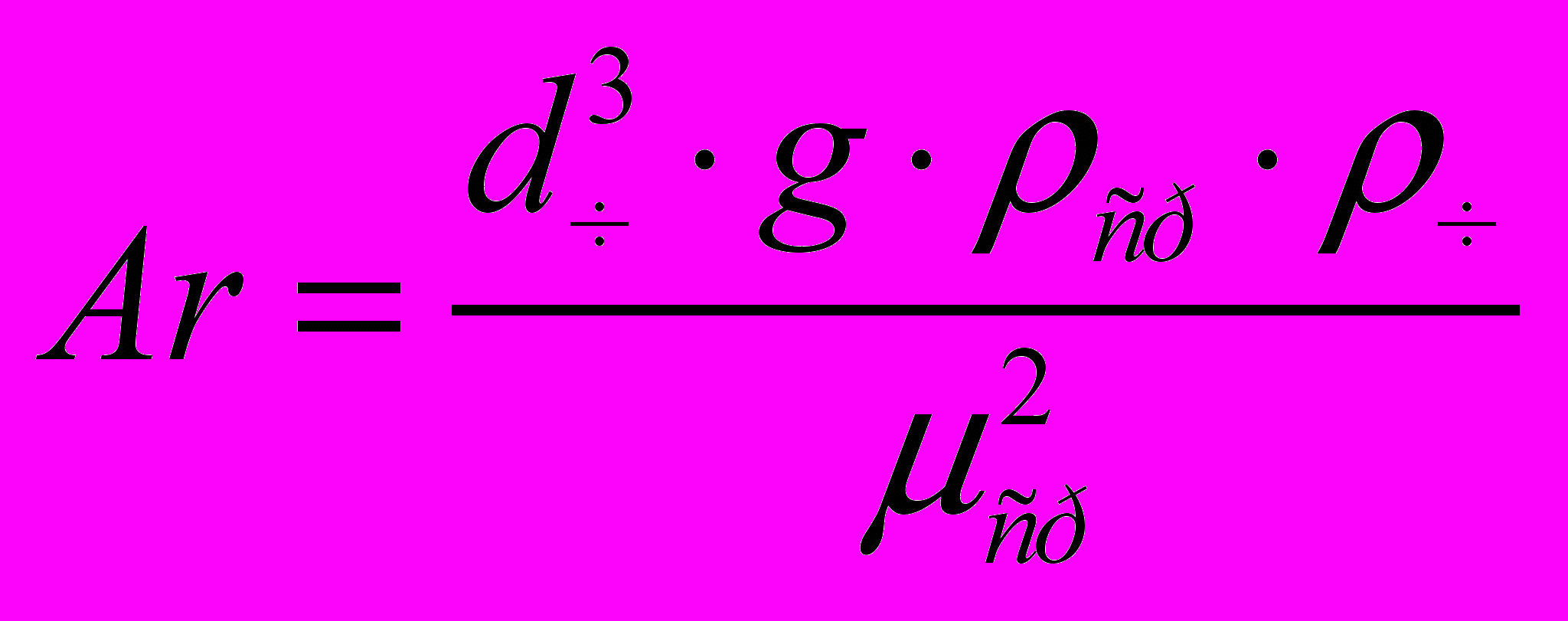, (3)


де 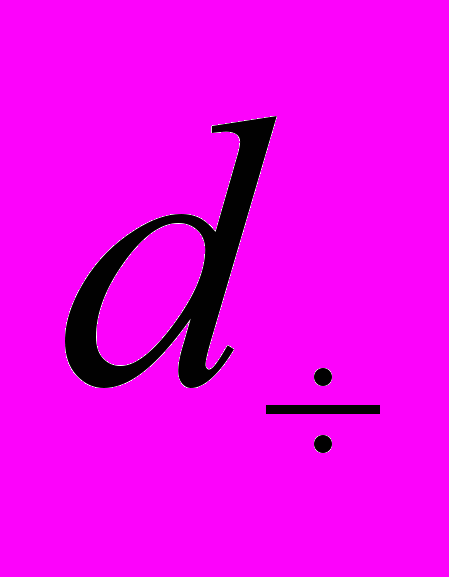– середній розмір часток в апараті, м3;

– в’язкість теплоносія при середній температурі;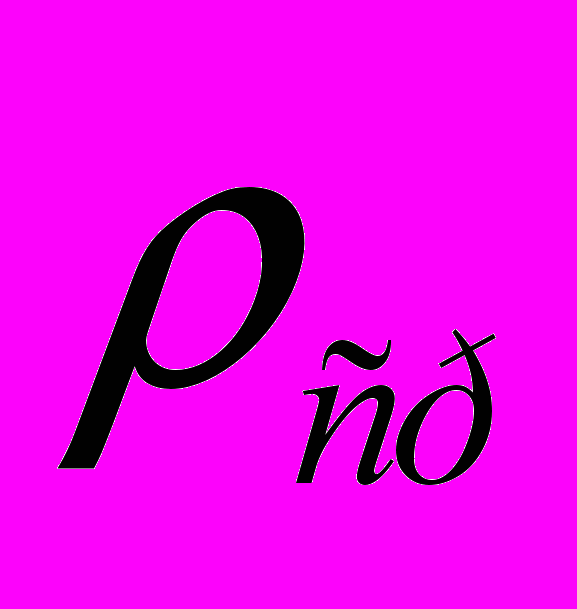

- щільність теплоносія при середній температурі;

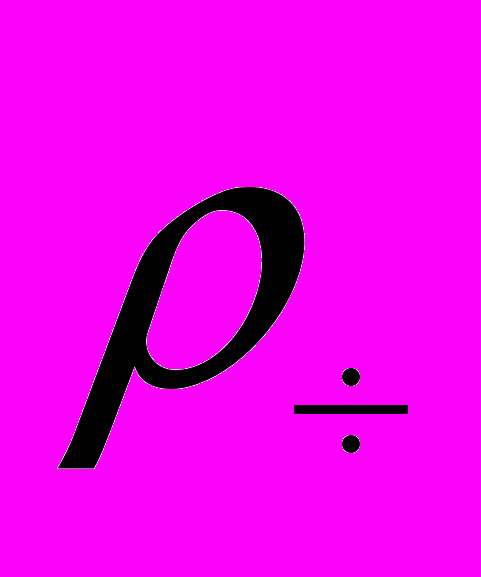– щільність часток готових гранул, кг/м3.


З формули (3) видно, що при однакових умовах проведення процесу сушки (однакових фізико-хімічних властивостей середовища (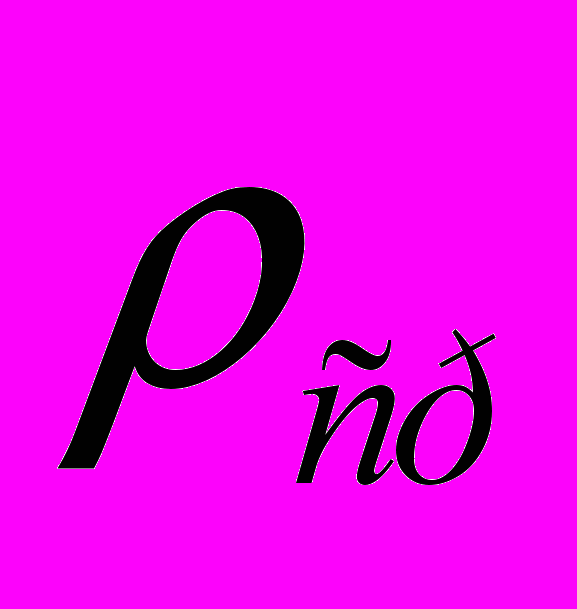, ) і часток (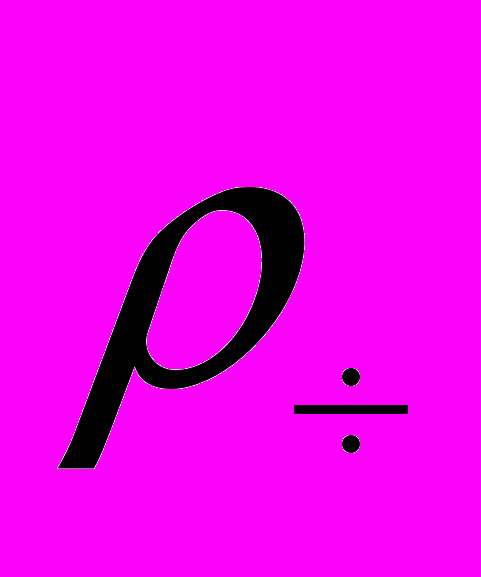), критерій Архимеда залежить тільки від розміру (діаметру) цих часток.

Підставив значення діаметра часток розміром від 0,0005 м до 0,002 м, визначимо критерій Архимеда по формулі (3). Данні зведені у таблицу 1.


Таблица 1 – Залежність занчення критерія Архимеда від діаметра часток, що знаходяяться у псевдозрідженому шарі

d, м
0,0005
0,0006
0,0007
0,0008
0,0009
0,001
0,0011
0,0012
0,0013
0,0014
0,0015
0,0016
0,0017
0,0018
0,0019
0,002

Ar
2158,097
3729,191
5921,817
8839,563
12586,02
17264,77
22979,41
29833,53
37930,7
47374,54
58268,61
70716,51
84821,83
100688,2
118419,1
138118,2


Тоді графік залежності крітерія Архимеда від діаметра часток в апараті представлена на рис.5.



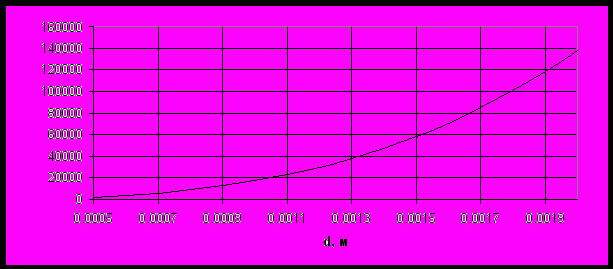Рисунок 5 – Графік залежності крітерія Архимеда від середнього діаметра часток в апараті


В логарифмічних координатах ця крива крива буде виглядати наступним чином (рис. 6).



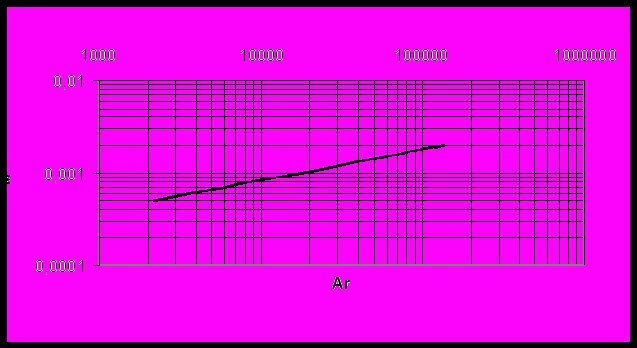
Рисунок 6 - Графік залежності крітерія Архимеда від середнього діаметра часток в апараті на логарифмічній шкалі


Из рис.6 вперше виведена залежність

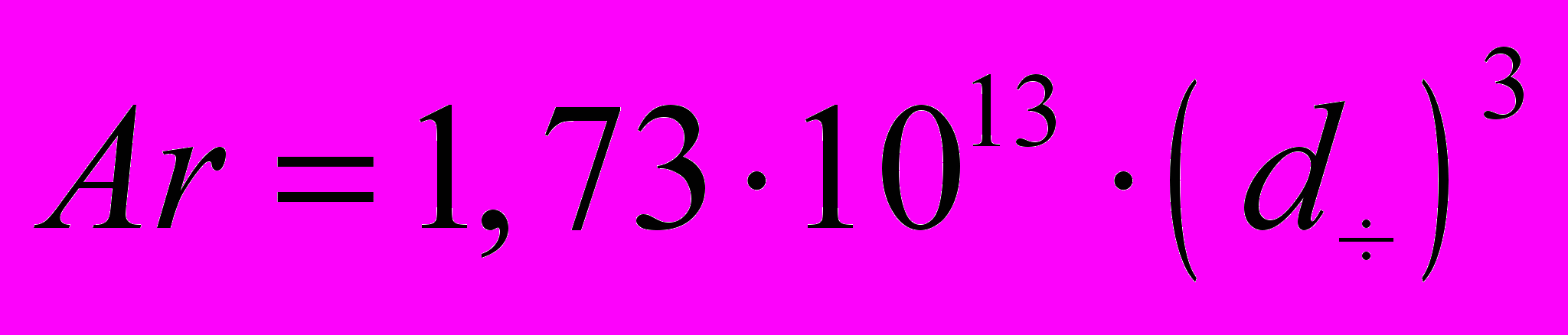, (4)

Рівняння (4) дозволяє визначити значення критерію Архимеда у робочому діапазоні діаметра часток в апараті. Такоже складена програма, яка дозволяє одержувати данне рівняння при зміні умов проведення процесу (однакових фізико-хімічних властивостях середовища (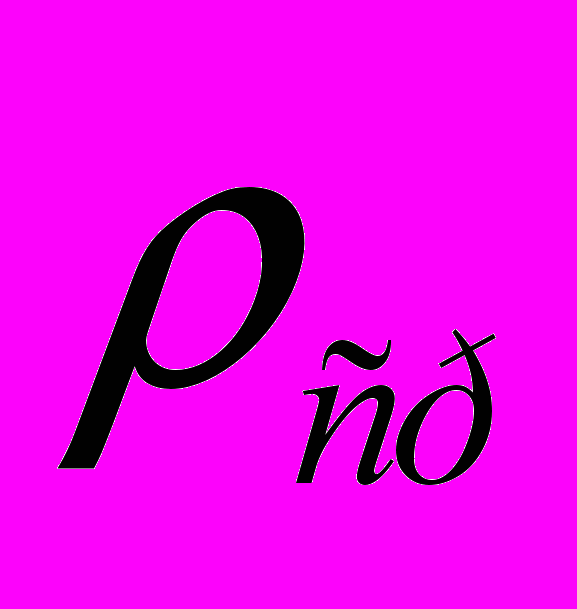, ) і часток (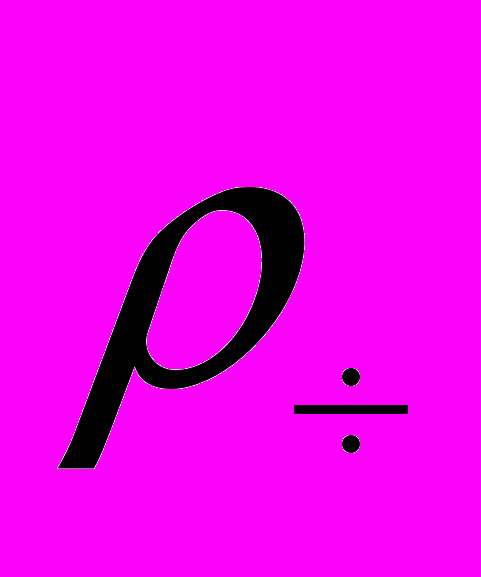), представлена на рис.7. Погрішність методу розрахунку (Δ) нікчемно мала.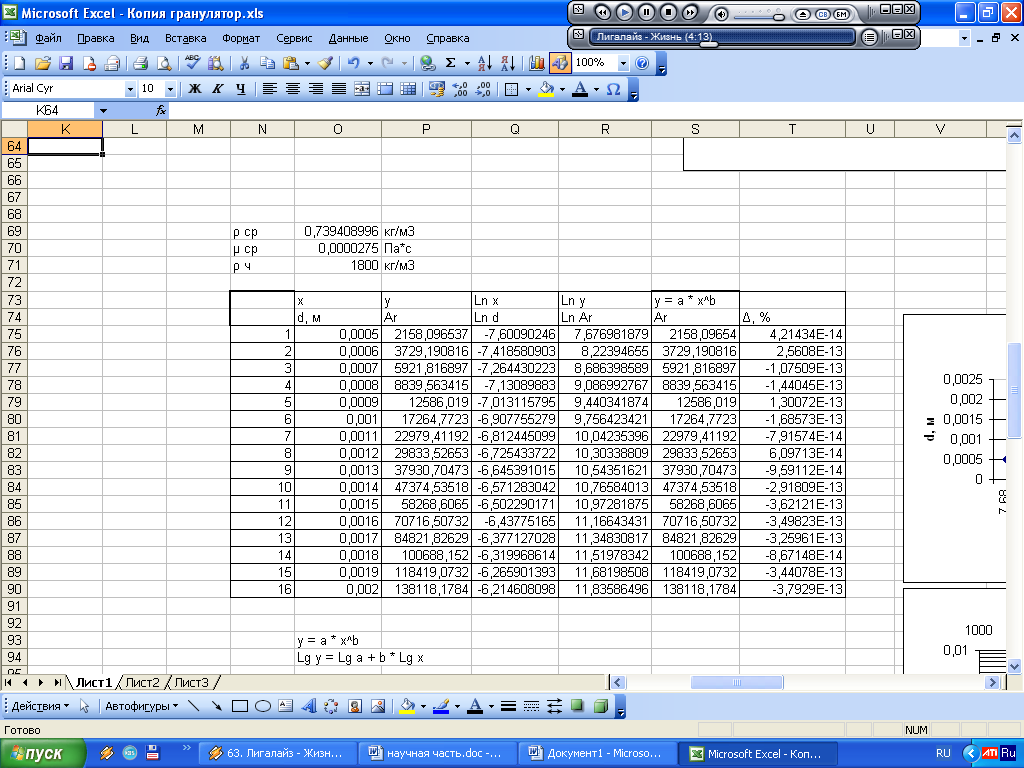






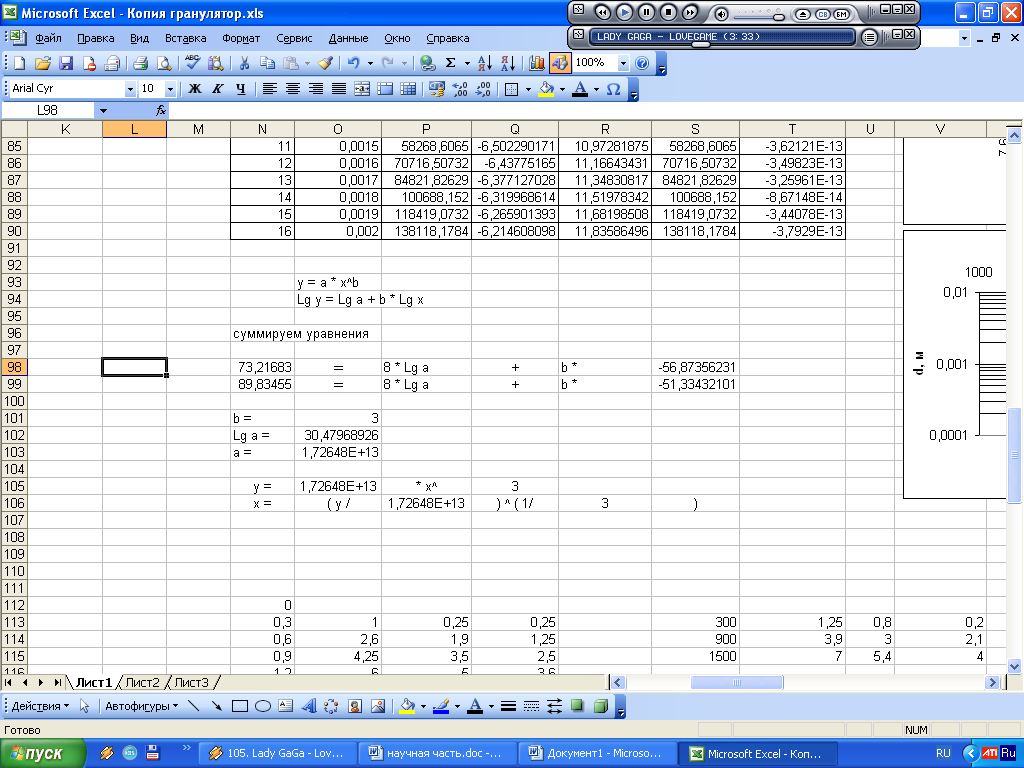
Рисунок 7 – Програма розрахунку залежності Ar = f (d)


2.5.2 Вибір оптимального метода розрахунку швидкості теплоносія


Швидкість потоку, при якому опір шару стає рівним вазі шару, що приходиться на одиницю площі поперечного перетину, і при якій частки нерухомого шару переходять у завислий стан, називається критичною швидкістю або швидкістю початка псевдозрідження. Для визначення критичної і робочої швидкостей руху теплоносія використовують різні методики розрахунку [16].

Горошко, Розенбаум і Тодес скористувавшись рівнянням Эргана для перепаду тиску при русі газу (рідини) через нерухомий зерністий шар одержали рівняння для визначення критичної швидкості псевдозрідження [17]:


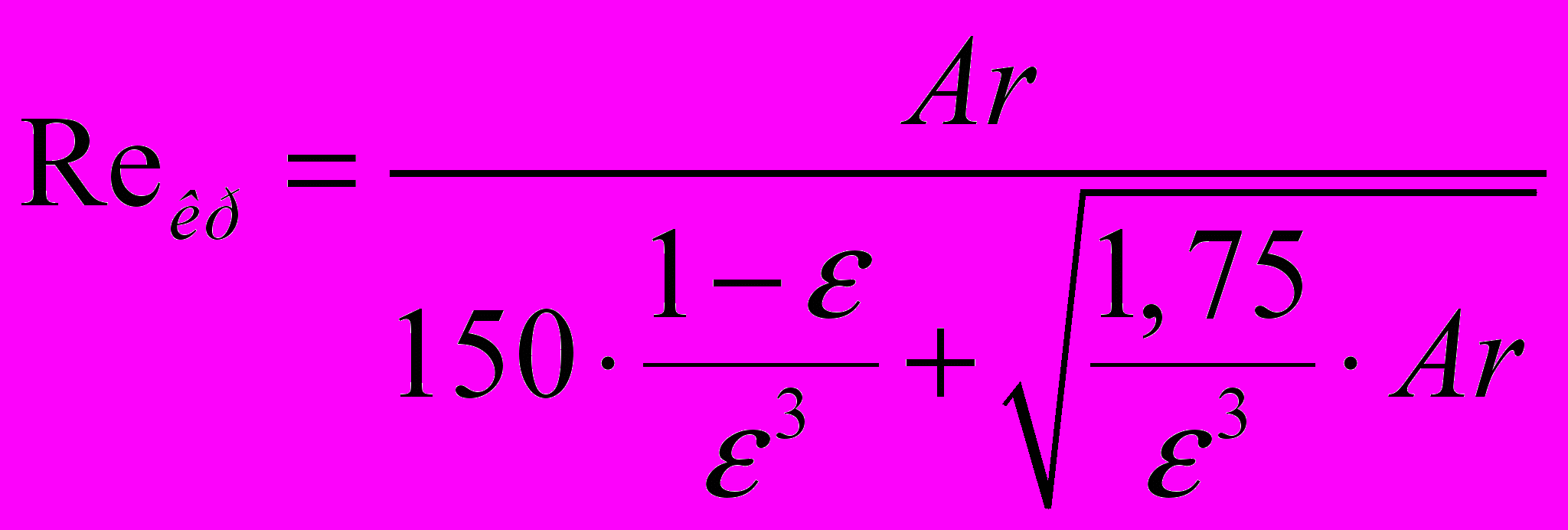(5)


Слід відмітити, що Рождественським [17] одержано уточнене рівняння:


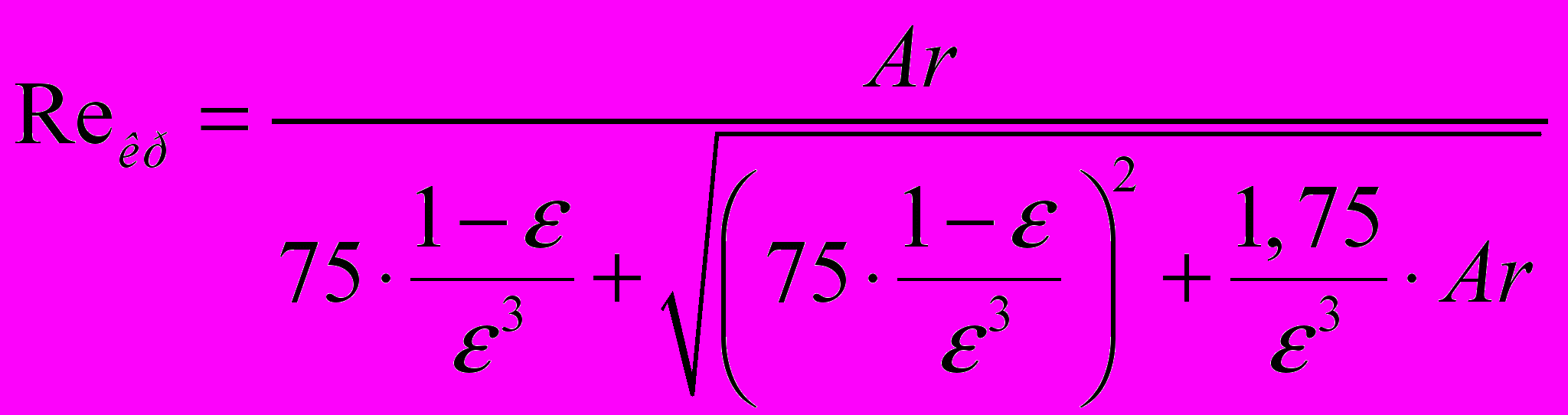(6)


Також авторами Горошко, Розенбаум і Тодес [17] запропонована узагальнююча полуемпірічна інтерполяційна формула для опису всього діапазону існування зрідженого шару:


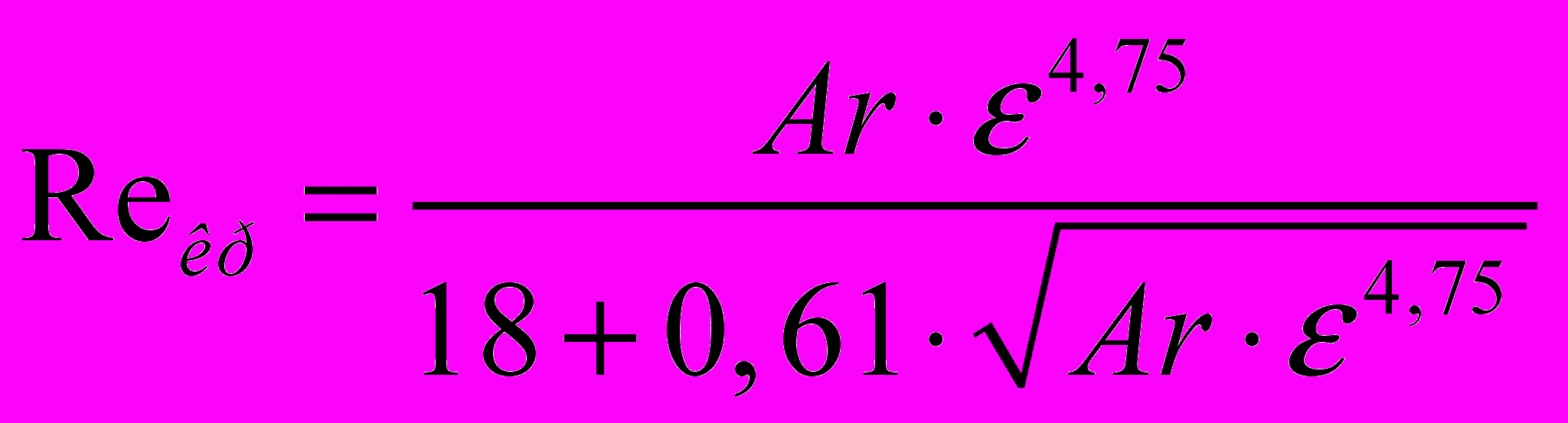(7)


Авторами Павлов, Романков і Носков [16] запропонований графічний метод визначення числа Рейнольдса в залежності від крітерія Архимеда або крітерія Лященко (рис.8):



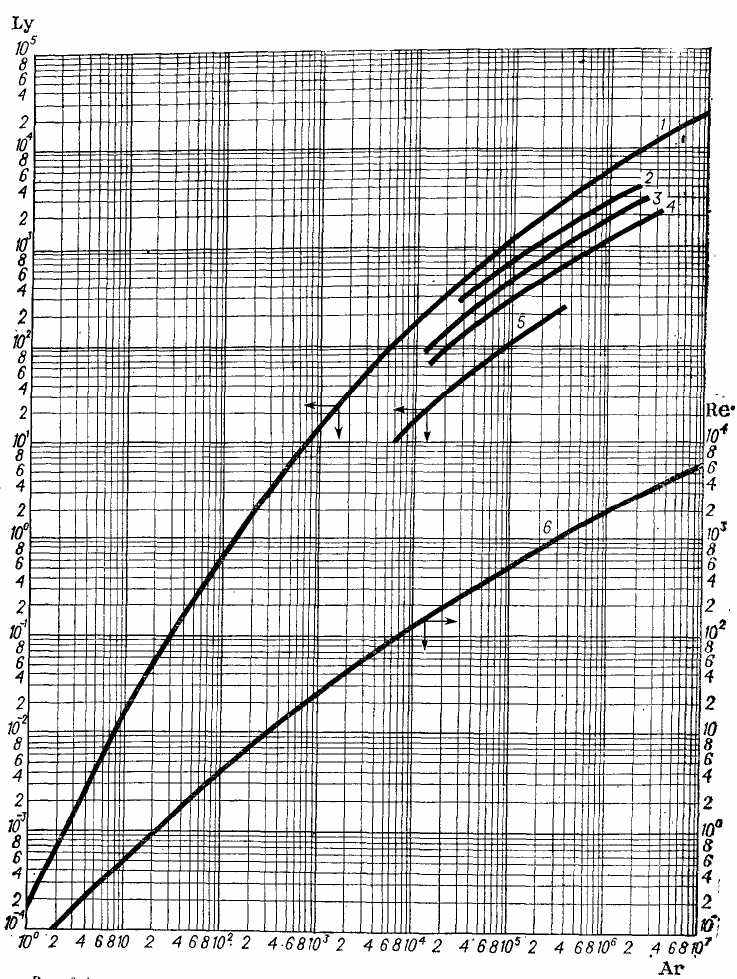
Рисунок 8 – Залежність крітерієв Рейнольдса Re і Лященко Ly від крітерія Архимеда Ar для осадження одиночної частки у нерухомому середовищі:

1 і 6 – шароподібні частки, 2 – скруглені, 3 – кутоваті, 4 – продовгуваті,

5 – пластинчасті.


Робоче значення крітерію Re вибираємо при порозності киплячого шару 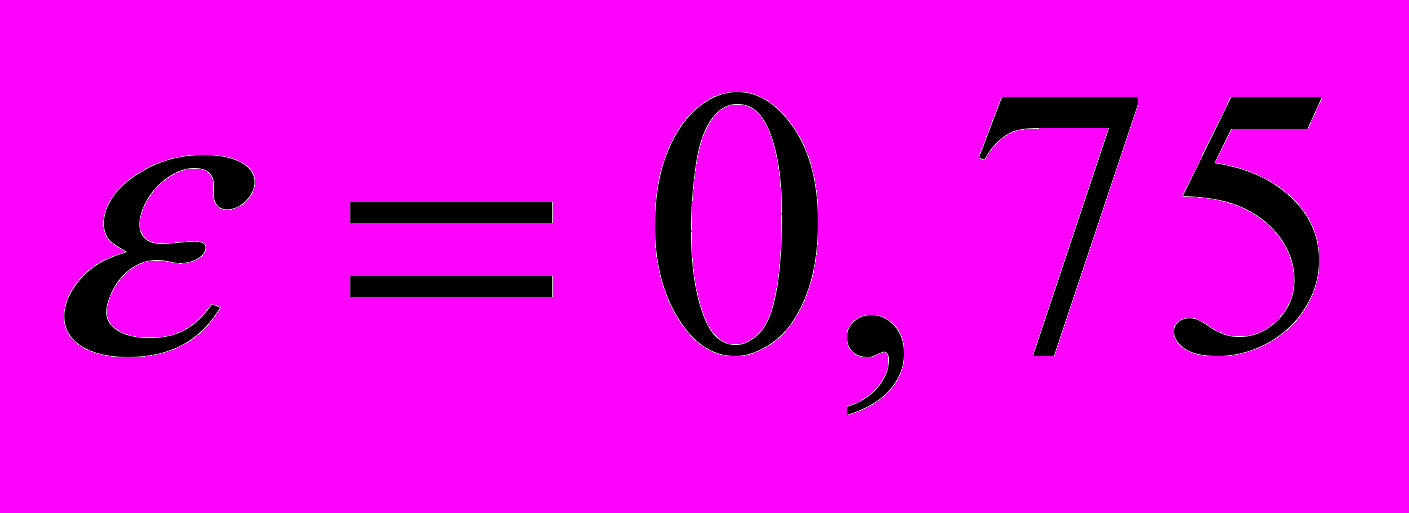, оскільки для процесів сушіння інтенсивність процесу тим вище, чим більше швидкість газів.

Підставив значення діаметру часток від 0,0005 м до 0,002 м, одержимо данні, необхідні для будови графіка залежності крітерія Рейнольдса від середнього діаметра часток в апараті з використанням різних методик розрахунку числа Рейнольдса. Данні зведені в табл.2. Графік залежності крітерія Рейнольдса від середнього діаметра часток в апараті представлений на рис.9.


Таблиця 2 – Залежність значення критерія Рейнольдса від діаметра часток, які знаходяться у псевдозрідженому шарі, в залежності від методики розрахунку

d, м
Re кр
Re кр
Re кр
Re кр




Емпірічна інтерполяційна формула
Горошко, Розенбаум, Тодес
Рождественский з сотр.
Графічний метод

0,0005
17,032
11,760
14,486
40

0,0006
25,833
17,486
21,126
60

0,0007
36,209
24,110
28,559
80

0,0008
47,9991
31,527
36,675
105

0,0009
61,065
39,656
45,401
130

0,001
75,290
48,428
54,683
160

0,0011
90,576
57,791
64,482
195

0,0012
106,840
67,700
74,766
230

0,0013
124,017
78,119
85,508
265

0,0014
142,047
89,018
96,689
310

0,0015
160,883
100,372
108,289
350

0,0016
180,482
112,159
120,292
390

0,0017
200,808
124,361
132,683
435

0,0018
221,831
136,960
145,452
475

0,0019
243,521
149,943
158,585
510

0,002
265,855
163,296
172,073
550



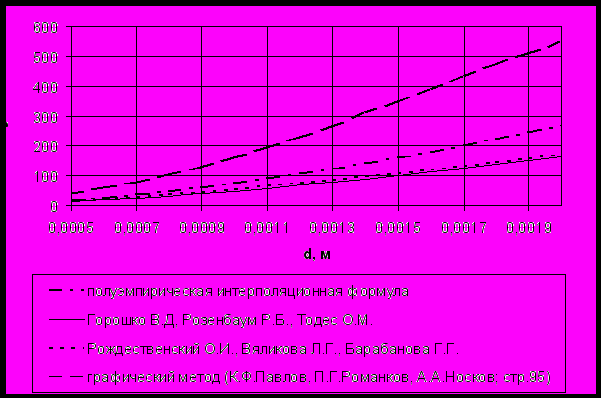
Рисунок 9 – Графік залежності крітерія Рейнольдса від середнього діаметра часток в апараті з використанням різних методик розрахунку


З графіка видно, що використання різних методик розрахунку числа Рейнольдса приводить до одержання значень, що відрізняються один від одного. Якщо за основний метод взяти розрахунок по полуемпірічній інтерполяційній формулі, то значення, отримані по інших методиках розрахунку, відрізнятимуться від основного методу на 35,7% (Горошко В.Д, Розенбаум Л.Г, Тодес О.М), 27,4% (Різдвяний О.І з сотр.) і 112,5% (Павлов, Романков, Шкарпеток). Так, наприклад, використання графічного методу, запропонованого авторами [16] (Павлов, Романков, Шкарпеток) дає дуже великі значення числа Рейнольдса із-за погрішностей, супроводжуючі будь-який графічний метод розрахунку. Тому використання цього методу розрахунку критерію Рейнольдса неприпустимо при проектуванні промислового устаткування.

Дві нижні криві, отримані при використанні методик, запропонованих авторами [17] і [14] дають дуже близькі результати, які практично збігаються між собою.

Правильне визначення критерію Рейнольдса істотно впливає на розрахунок швидкості руху теплоносія і, як наслідок, на розміри апарату (геометричні параметри решітки і висоти сепараційного простору). Тому вибір методики розрахунку числа Рейнольдса стає одним з основних завдань, які ставляться перед розробниками устаткування для хімічних підприємств.

Робоча швидкість руху теплоносія визначається по формулі:

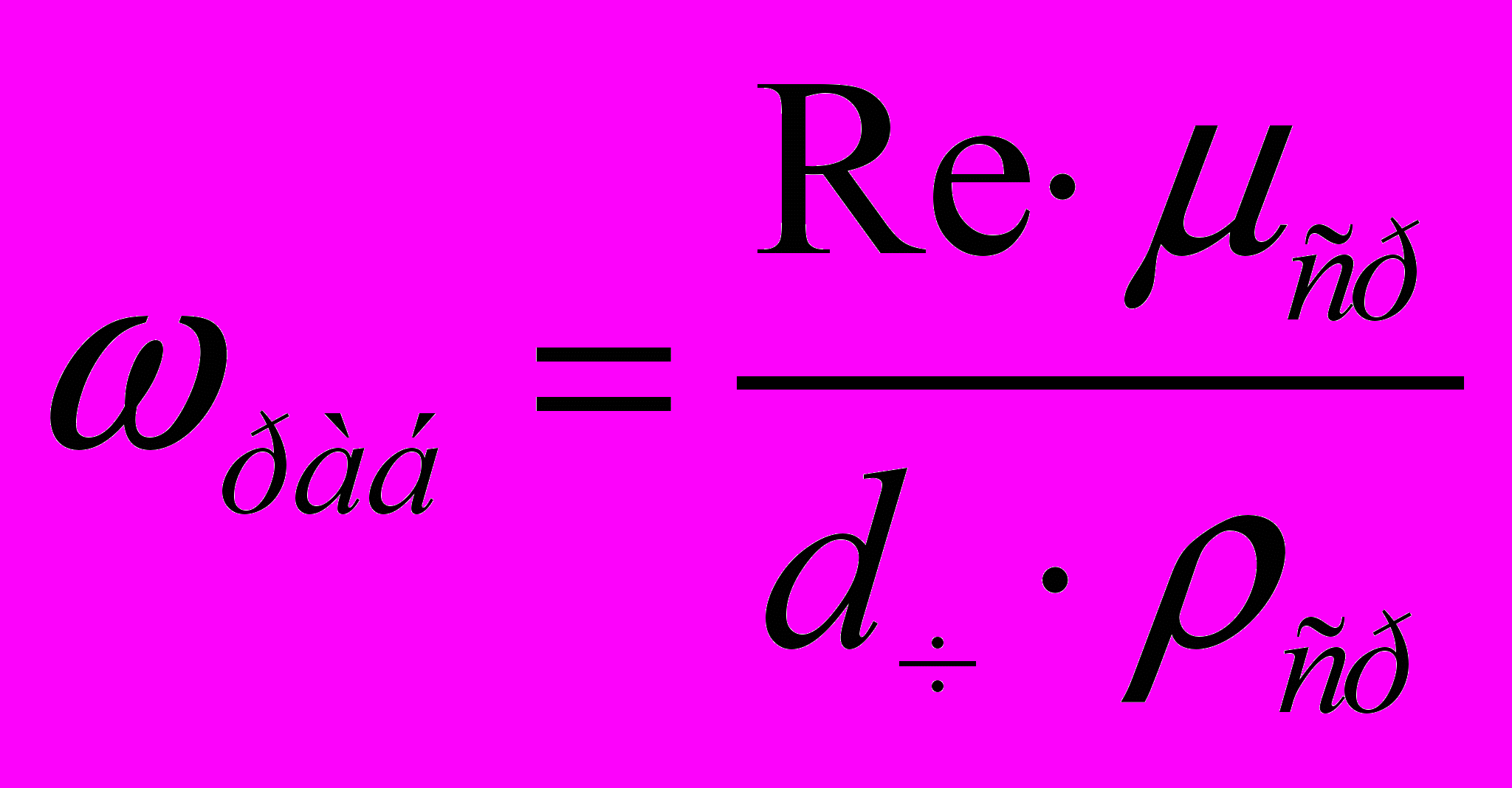(8)

Також для розрахунку робочої швидкості руху теплоносія можна скористатися методикою, запропонованою авторами [17] (Романков, Рашковская). Вона полягає у визначенні критичної швидкості псевдозрідження і робочого числа псевдозрідження для досягнення заданої порозності шару.

Критична швидкість початка псевдозрідження визначається по формулі [16].

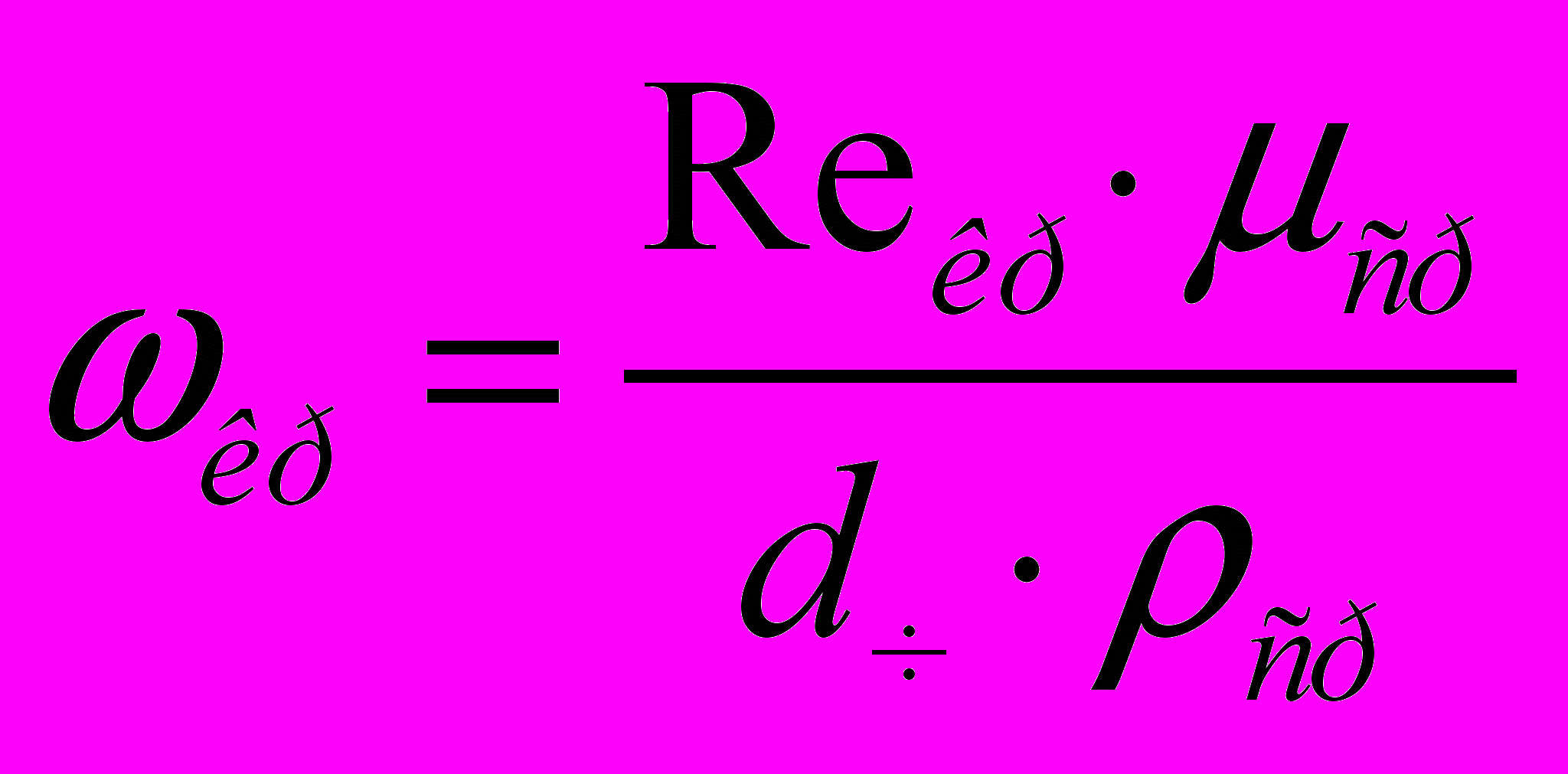(9)

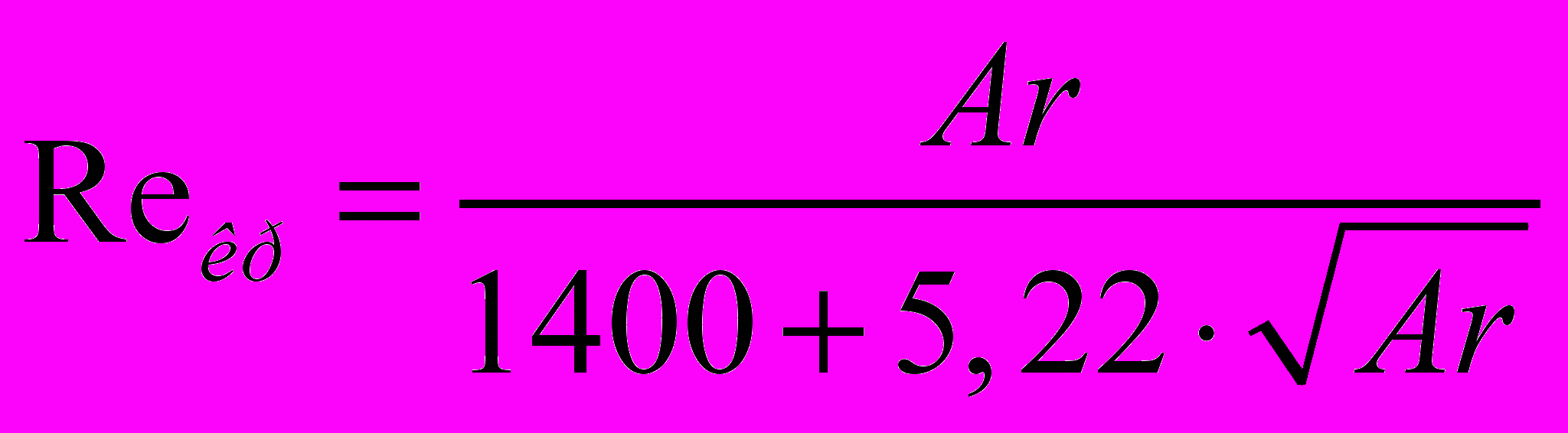где (10)


Робочу швидкість руху теплоносія визначаємо по формулі:


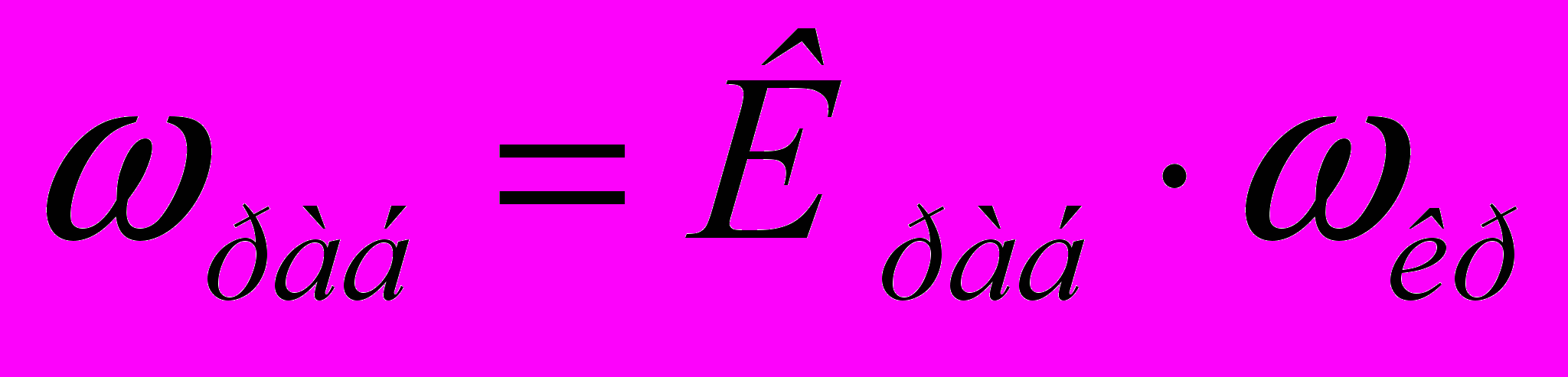(11)


де 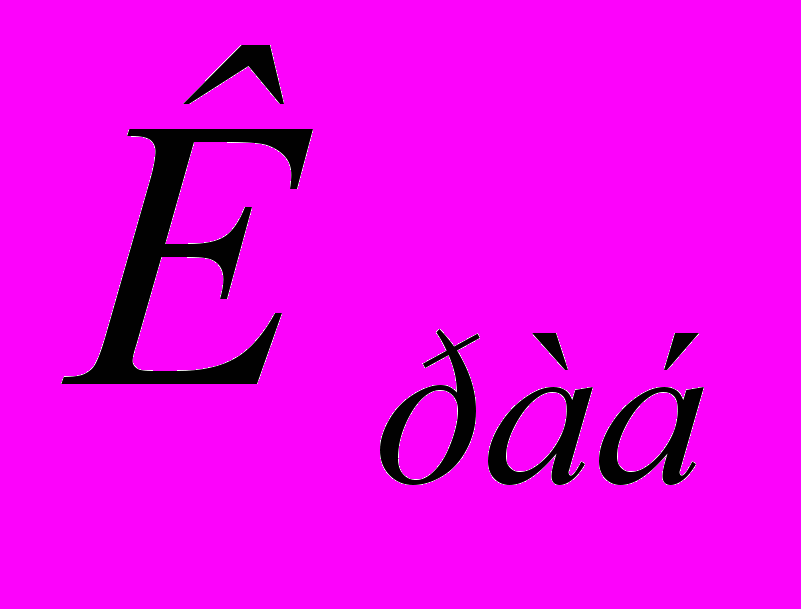- робоче число псевдозрідження.


Робоче число псевдозрідження визначаємо по формулі:


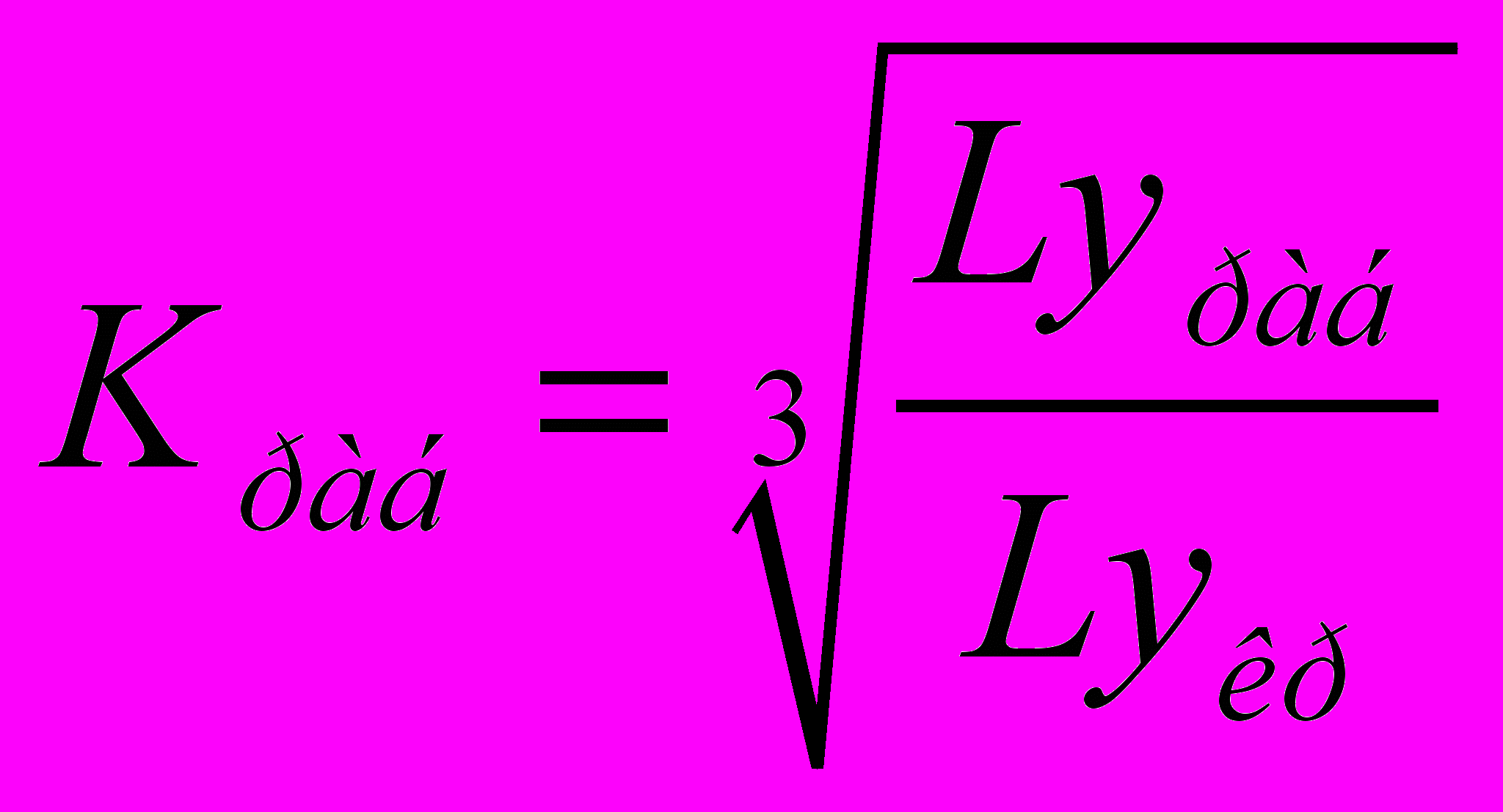(12)


де 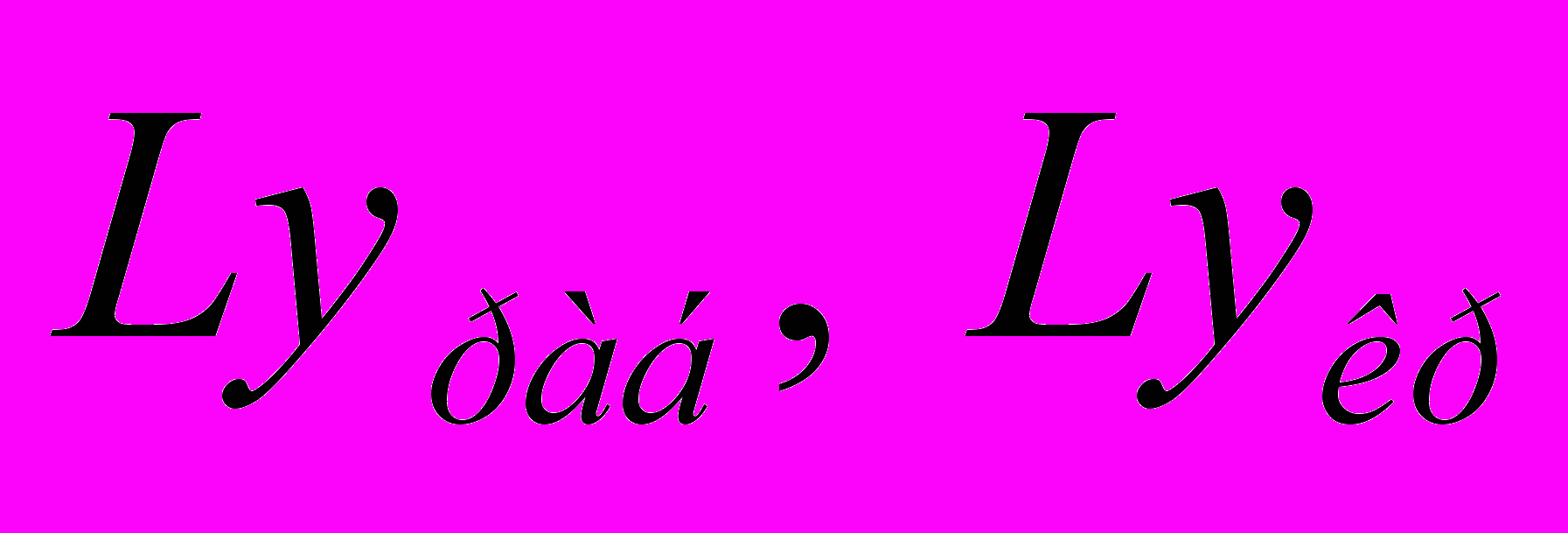- критерій Лященко відповідно при робочій швидкості руху теплоносія і при критичній швидкості початкуа псевдозрідження.

Критерій Лященко визначаємо по графіку (рис.10). Він залежить від числа Архимеда і порозності шару [16]. Практично порозность нерухомого насипного шару шароподібних часток однакового діаметру коливається у межах 0,38 – 0,42; в розрахунках приймається середне значення 0,40 [16]. Відповідно 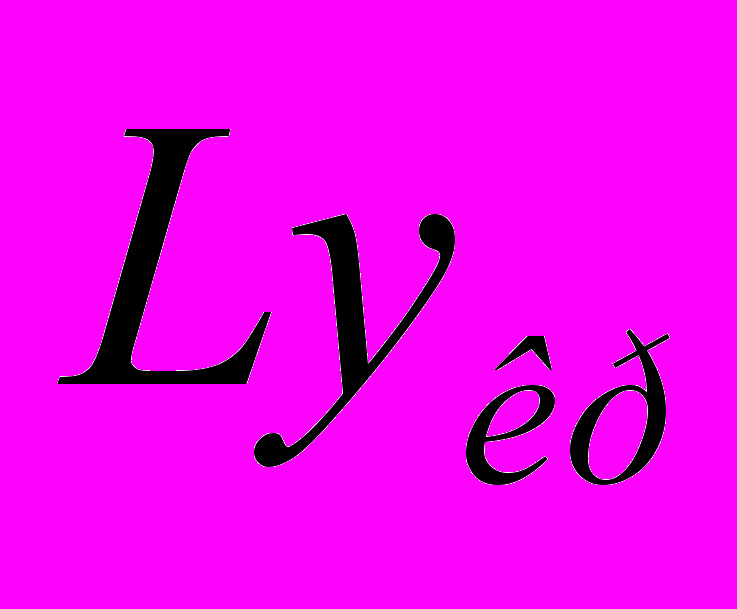визначаємо по рис.4 при ε = 0,4. Робоче значення критерія Лященко 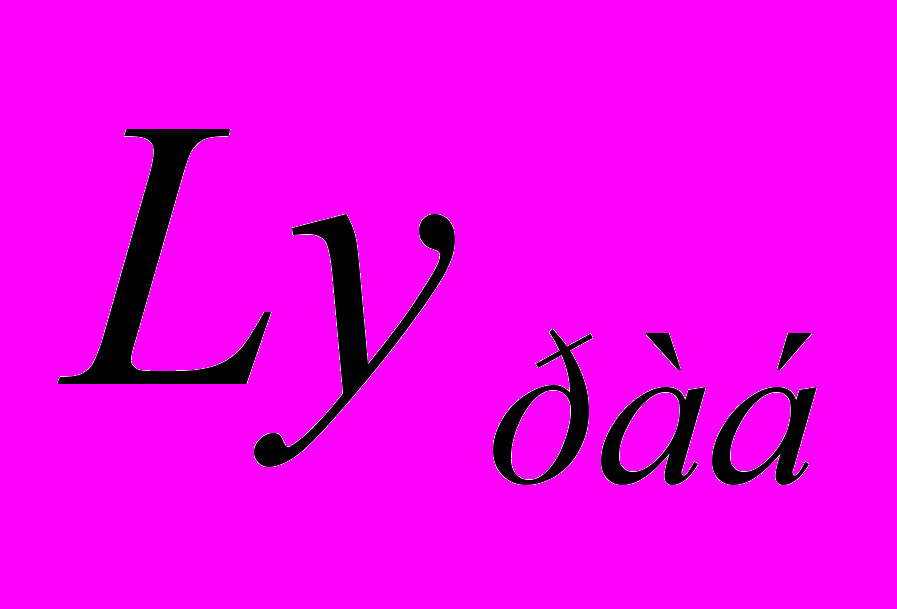визначаємо при порозності ε = 0,75, оскільки для процесів сушки, які йдуть у першому періоді, інтенсивність процесу тим вище, чим більше швидкість газів.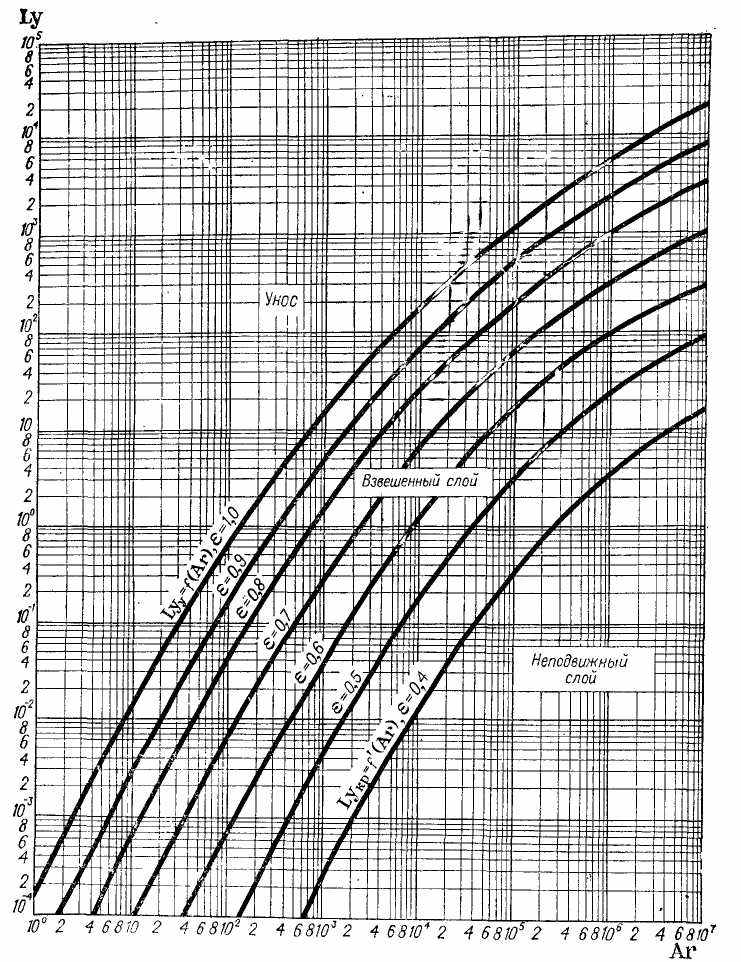



Рисунок 10 – Графік залежності Ly = f (Ar, ε)


Порівнюючі одержані данні по робочим швидкостям руху теплоносія, які були визначені по різним методикам розрахунку. Данні зведені в табл.3.


Таблиця 3 – Залежність значення робочої швидкості теплоносія від діаметру часток, що знаходяться у псевдозрідженому шарі, в залежності від методики розрахунку


d, м
ω роб, м/с
ω роб, м/с
ω роб, м/с
Ly кр
Ly роб
К роб
Re кр
ω кр
ω роб, м/с




Емпірична формула
[23]
[24]
Графічний метод [4]

0,0005
1,2669
0,8748
1,0775
0,0010
35
32,71
1,31
0,0977
3,1969

0,0006
1,6013
1,0839
1,3095
0,0025
65
29,62
2,17
0,1345
3,9843

0,0007
1,9238
1,2810
1,5174
0,0050
100
27,14
3,29
0,1746
4,7402

0,0008
2,2315
1,4657
1,7050
0,0090
150
25,54
4,68
0,2173
5,5518

0,0009
2,5235
1,6388
1,8762
0,0125
165
23,63
6,34
0,2619
6,1905

0,001
2,8002
1,8011
2,0338
0,0240
250
21,84
8,28
0,3078
6,7230

0,0011
3,0624
1,9539
2,1802
0,0410
350
20,44
10,49
0,3546
7,2464

0,0012
3,3113
2,0982
2,3172
0,0590
420
19,24
12,96
0,4017
7,7281

0,0013
3,5480
2,2349
2,4463
0,0900
560
18,39
15,70
0,4490
8,2591

0,0014
3,7736
2,3648
2,5686
0,1200
690
17,92
18,68
0,4962
8,8902

0,0015
3,9890
2,4887
2,6850
0,1500
800
17,47
21,91
0,5431
9,4893

0,0016
4,1953
2,6071
2,7962
0,1900
890
16,73
25,36
0,5896
9,8646

0,0017
4,3932
2,7207
2,9028
0,2500
1050
16,13
29,05
0,6355
10,2525

0,0018
4,5835
2,8299
3,0053
0,3000
1150
15,65
32,94
0,6807
10,6530

0,0019
4,7668
2,9351
3,1042
0,3500
1300
15,49
37,05
0,7252
11,2312

0,002
4,9438
3,0366
3,1999
0,4000
1400
15,18
41,35
0,7690
11,6757


Графік залежності робочої швидкості руху теплоносія від середнього діаметра часток в апараті з використанням різних методик розрахунку представлений на рис.11.



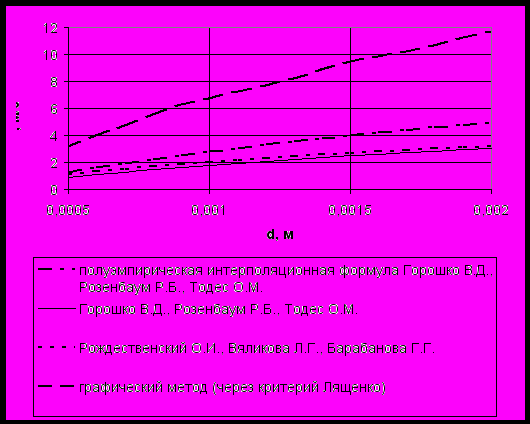
Рисунок 11 – Графік залежності робочої швидкості руху теплоносія від середнього діаметра часток в апараті з використанням різних методик розрахунку


З рис.11 видно, що використання різних методик розрахунку числа Рейнольдса приводить до одержання значень, що істотно відрізняються один від одного. Так, наприклад, використання графічного методу, запропонованого авторами [16] (Романков, Рашковская) дає дуже великі значення робочої швидкості теплоносія і, як наслідок, дуже занижені значення розмірів апарату. Із-за погрішностей, супроводжуючих будь-який графічний метод розрахунку (погрішності, пов'язані з недосконалістю зорового апарату і з ціною ділення вимірювальних приладів) використання цієї методики при проектуванні промислового устаткування неприпустимо.

Використання методик, запропонованих авторами [17] (Горошко В.Д, Розенбаум Л.Г, Тодес О.М) і [14] (Різдвяний О.І з сотр.) дають близькі значення. Але дуже малі значення робочої швидкості руху теплоносія приводять до збільшення геометричних розмірів апарату і зниження інтенсивності тепло- і масообміну. Тому предпочтітельней використання вищих швидкостей по газу.

Діаметр грат апарату розраховується по формулі:


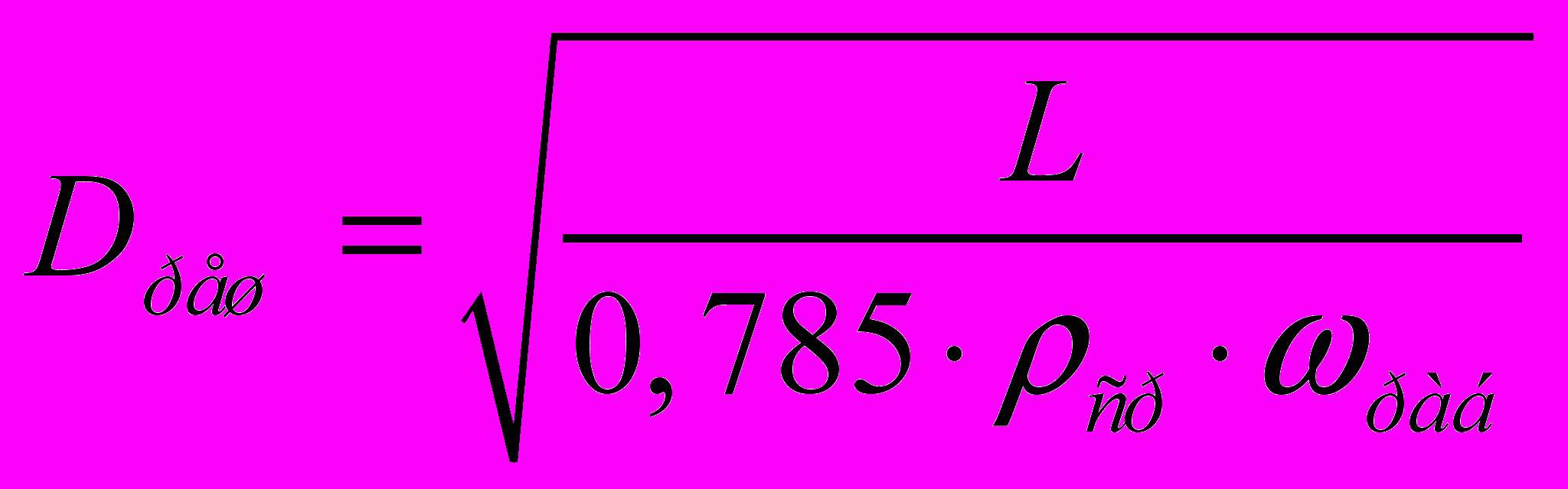(13)


де L – масові витрати теплоносія.


Якщо прийняти, що витрати теплоносія для проведення процесу грануляції і сушки не змінюється, то стає очевидним вплив швидкості руху теплоносія на розміри апарату. Відповідно вибір оптимального методу розрахунку швидкості теплоносія дозволить отримати точніші дані по розмірах апарату. На рис.12 показана залежність діаметру решітки апарату D від середнього діаметру d часток, що знаходяться в апараті при використанні різних методик розрахунку швидкості руху теплоносія.



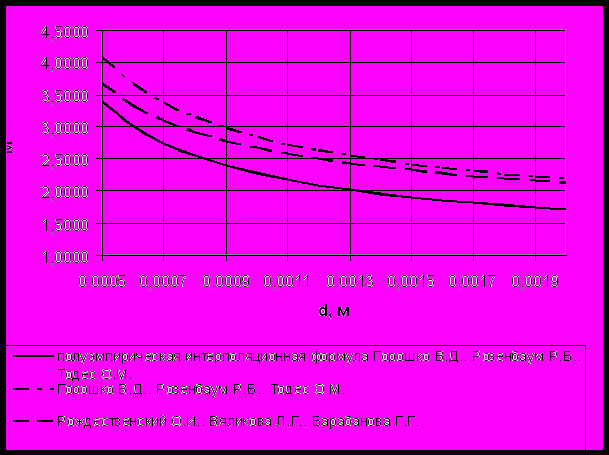
Рисунок 12 – Залежність D = f (d) при використанні різних методик розрахунку швидкості руху теплоносія

З рис.12 видно, що при використанні полуемпіричної інтерполяційної формули Горошко В.Д, Розенбаума Л.Г, Тодеса О.М значення геометричних параметрів апарату (діаметру решітки) за однакових умов будуть менші, ніж при використанні інших методик. З рис.11 видно, що за однакових умов протікання процесу грануляції і сушки робоча швидкість зріджуючого агента при використанні полуемпіричної інтерполяційної формули матиме великі значення, ніж при використанні методик, запропонованих авторами [17] і [16]. Оскільки для процесів сушки, які проходять у першому періоді, інтенсивність процесу тим вище, чим більше швидкість газів, то вживання полуемпіричної інтерполяційної формули для розрахунку критерію Рейнольдса і визначення робочої швидкості руху теплоносія рекомендується при проектуванні апаратів хімічної промисловості.


ВИСНОВКИ ПО ГЛАВІ:


1. Оптимальною конструкцією гранулятора є циліндро-конічний апарат з кутом розкриття конуса 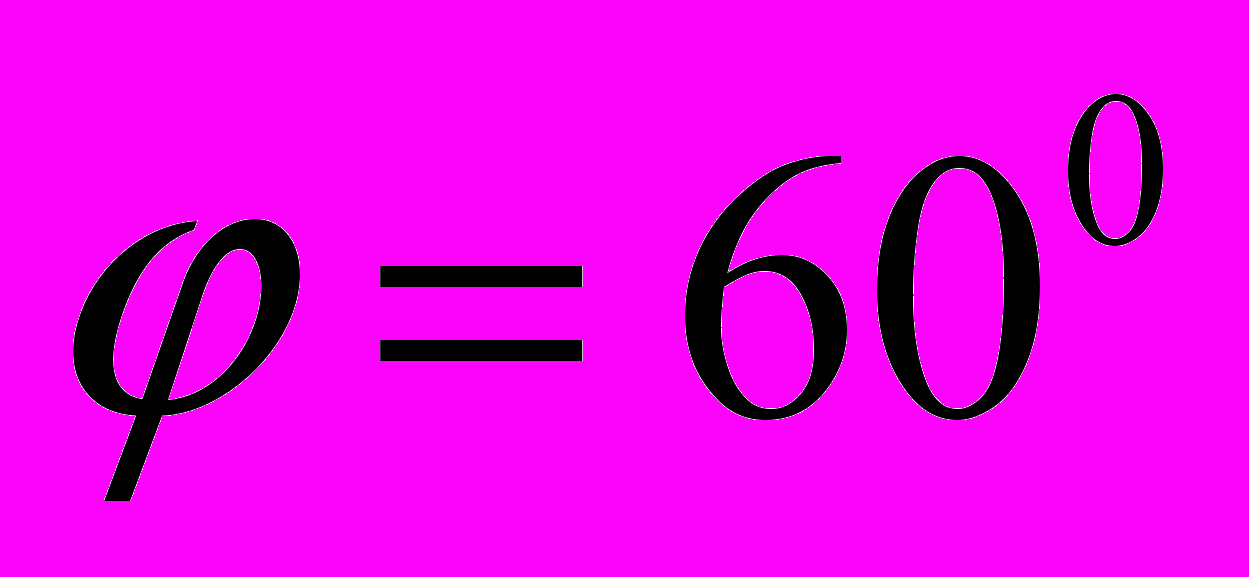. До переваг таких апаратів можна віднести пневмокласифікацію часток з сепарацією дрібної фракції. Також апарати даної конструкції мають оптимальні значення гідравлічного опору, коефіцієнтів тепло- и масообміну, можливість регулювання часу перебування часток в апараті, рівномірне зрошення рідини по всьому перетину апарата, стабільний псевдозріджений шар.

2. Вибрана опорна решітка перфорованого типу, яка забезпечує зниження флуктуацій тиску, стабілізацію завислого шару, зменшення гідравлічного опору, зниження витрат на створення і підтримання псевдозрідженого шару. Такі решітки мають просту конструкцію, вони дешеві у виготовлення і обслуговуванні.

3. Визначені оптимальна конструкція і місце розташування форсунки. Вибрана форсунка відцентрово-струйного типу з циліндричним вкладишем. Ці форсунки найбільш прості по конструкції і економічні в споживанні енергії. Форсунка розташована всередині гранулятора у верхній його частині.

4. В результаті аналізу різних методик розрахунку апаратів псевдозрідженого шару вибраний оптимальний метод розрахунку швидкості теплоносія і діаметра решітки. Обгрунтовано застосування полуемпірічної інтерполяційної формули Горошко В.Д, Розенбаума Л.Г, Тодеса О.М для розрахунку критерія Рейнольдса і визначення робочої швидкості руху теплоносія при проектуванні апаратів для виробництва органо-мінеральних добрив.


Аналіз одержаних даних дозволяє провести розрахунок гранулятора. Існує методика ручного розрахунку, в якій розраховуються матеріальні потоки, швидкість теплоносія в апараті, розмір решітки і сепараційного простору, часу перебування матеріалу в апараті. Ця методика вважається некоректною, оскільки можуть бути помилки при розрахунках і округлюванні значень, а також низька швидкість обчислюванняя. Тому для прискорення процесу обчислювання, підвищення якості проектування розроблена програма технологічного розрахунку апарата псевдозрідженого шару.

При розрахунках матеріальних потоків проводиться обчислення:
  • кількості суспензії і видаляємої вологи;
  • кількості абсолютно сухої речовини;
  • кількості мінеральних речовин;
  • витарти азотних, фосфорних і калійних добрив;
  • кількості органічних добрив у готовому продукті;
  • кількості мінеральних добрив, яке необхідго внести у суспензію для одержання заданого співвідношення поживних речовин;
  • загальних витрат мінеральних компонентів;
  • сумарної вологості мінеральних добрив, які додаються у суспензію;
  • кількості органічних добрив, які необхідно додавати у суспензію;
  • вологості суспензії до розбавлення її водою до заданої вологості;
  • кількості води, необхідної для розбавлення суспензії до необхідної вологості.


При визначенні швидкості теплоносія в апараті розраховуються:
  • критерій Архимеда для середнього розміра часток, що знаходяться в апараті;
  • критерій Архимеда для мінімального розміра часток, що знаходяться в апараті;
  • критерій Рейнольдса для середнього розміра часток, що знаходяться в апараті;
  • критерій Рейнольдса для мінімального розміра часток, що знаходяться в апараті;
  • робоча швидкість руху теплоносія в апараті;
  • швидкіть вітання часток мінімального розміру.


При визначенні розмірів решітки розраховуються:
  • повна площа решітки;
  • діаметр решітки.


При визначенні розмірів сепараційного простору розраховуються:
  • площа сепараційного простору;
  • діаметр сепараційного простору.


При визначенні часу перебування матеріалу в сушарці розраховуються:
  • маса матеріалу, що знаходиться в апараті;
  • час перебування матеріала в сушарці.