Принятие решений и оценивание

Вид материала

Реферат

Содержание Многообразие задач принятия решений Принятие решений как реализация цели Структура процесса принятия решения. Классификация задач принятия решений Языки описания методов принятия решений Критериальный язык. Язык последовательного бинарного выбора Обобщенный язык функций выбора Методы оценивания в процессе принятия решения Групповой выбор Выбор в условиях неопределенности Принятие решений в условиях риска Критерий ожидаемого значения (КОЗ). Критерий "ожидаемого значения - дисперсия". Критерий предельного уровня. Критерий наиболее вероятного исхода. Учет неопределенных факторов, заданных законом распределения. Постановка задачи стохастического программирования Метод статистического моделирования Байесовский подход в вероятностных задачах принятия решения О некоторых ограничениях оптимизационного подхода Экспертные методы выбора ... Полное содержание

Подобный материал:

• Лекция 03. 04. 07 Принятие решений как функция менеджмента, 65.61kb.
• 2 Принятие решений, 23.85kb.
• Темы курсовых работ по дисциплине «Принятие и разработка управленческих решений» (прур), 28.44kb.
• Рабочая программа дисциплины (модуля) «принятие и исполнение государственных решений», 543.17kb.
• Отделение Прикладной Математики и Информатики программа дисциплины, 225.44kb.
• Методические указания к изучению курса «управленческий учет и принятие решений», 338.51kb.
• «Принятие стратегических решений», 98.01kb.
• Демонстрационная версия рабочей программы по курсу «Принятие решений в области охраны, 73.81kb.
• Рабочая программа дисциплины (модуля) нечеткая математика и принятие решений, 131.73kb.
• Принятие решений, 480.56kb.

Министерство образования РФ

Ульяновский Государственный Технический Университет

Кафедра «ВТ»

Дисциплина «Инженерия знаний»


Реферат на тему «Принятие решений и оценивание»


Выполнила студентка Батанова В.А.

Проверил: Соснин П.И.


Ульяновск 2001


Содержание

Многообразие задач принятия решений

Принятие решений как реализация цели

Определение: принятие решения ("выбор") есть действие над множеством альтернатив, в результате которого исходное множество альтернатив сужается, т.е. происходит его редукция.

Выбор является действием, придающим всей деятельности целенаправленность. Именно через акты выбора реализуется подчиненность всей деятельности определенной цели или совокупности взаимосвязанных целей.

Таким образом, для того, чтобы стал возможен акт выбора, необходимо следующее:

• порождение или обнаружение множества альтернатив, на котором предстоит совершить выбор;
  

• определение целей, ради достижения которых осуществляется выбор;
  

• разработка и применение способа сравнения альтернатив между собой, т.е. определение рейтинга предпочтения для каждой альтернативы согласно определенным критериям, позволяющим косвенно оценивать, насколько каждая альтернатива соответствует цели.
  

Таким образом, принятие решений следует воспринимать не как единовременный акт, а как последовательный процесс.

Выдвинутые выше положения носят достаточно общий характер, обычно подробно исследуемый психологами. Более близкой с точки зрения инженера будет следующая схема процесса принятия решения. Эта схема включает в себя следующие компоненты:

• анализ исходной ситуации;
  
• анализ возможностей выбора;
  
• выбор решения;
  
• оценка последствий решения и его корректировка.
  

Современные работы в области поддержки принятия решений выявили характерную ситуацию, которая состоит в том, что полная формализация нахождения наилучшего (в определенном смысле) решения возможна только для хорошо изученных, относительно простых задач, тогда как на практике чаще встречаются слабо структурированные задачи, для которых полностью формализованных алгоритмов не разработано (если не считать полного перебора и метода проб и ошибок). Вместе с тем опытные, компетентные и способные специалисты часто делают выбор, который оказывается достаточно хорошим. Поэтому современная тенденция практики принятия решений в естественных ситуациях состоит в сочетании способности человека решать неформализованные задачи с возможностями формальных методов и компьютерного моделирования: диалоговые системы поддержки принятия решений, экспертные системы, адаптивные человеко–машинные автоматизированные системы управления, нейронные сети и когнитивные системы.

Структура процесса принятия решения.

Стимул к появлению проблем


Разработка постановки задачи


Пересмотр постановки задачи


Определение целей и критериев


Разработка математической модели





Пересмотр проблемы



Определение ограничений

Выбор метода решения и разработка алгоритма



Оценка полученного результата


Составление списка альтернатив


Оценка альтернатив и выбор оптимальной





Исполнение решения


Сбор информации и прогноз


Анализ решения

Принятие решения

Классификация задач принятия решений

Множественность задач принятия решений связана с тем, что каждая компонента ситуации, в которой осуществляется принятие решений, может реализовываться в качественно различных вариантах.

Перечислим только некоторые из этих вариантов:

• множество альтернатив, с одной стороны, может быть конечным, счетным или континуальным, а с другой, – закрытым (т.е. известным полностью) или открытым (включающим неизвестные элементы);
  
• оценка альтернатив может осуществляться по одному или нескольким критериям, которые, в свою очередь, могут иметь количественный или качественный характер;
  
• режим выбора может быть однократным (разовым), или многократным, повторяющимся, включающим обратную связь по результатам выбора, т.е. допускающим обучение алгоритмов принятия решений с учетом последствий предыдущих выборов;
  
• последствия выбора каждой альтернативы могут быть точно известны заранее (выбор в условиях определенности), иметь вероятностный характер, когда известны вероятности возможных исходов после сделанного выбора (выбор в условиях риска) или иметь неоднозначный исход с неизвестными вероятностями (выбор в условиях неопределенности);
  
• ответственность за выбор может отсутствовать, быть индивидуальной или групповой;
  
• степень согласованности целей при групповом выборе может варьироваться от полного совпадения интересов сторон (кооперативный выбор) до их противоположности (выбор в конфликтной ситуации). Возможны также промежуточные варианты: компромисс, коалиция, нарастающий или затухающий конфликт.
  

Различные сочетания перечисленных вариантов и приводят к многочисленным задачам принятия решений, которые изучены в различной степени.

В общем случае все факторы, то которых зависит эффективность выбора, можно разбить на две группы:

• контролируемые (управляемые) факторы, выбор которых определяется лицами, принимающими решения;
  
• неконтролируемые (неуправляемые) факторы, характеризующие условия, в которых осуществляется выбор и на которые лица, принимающие решения, влиять не могут. В состав неконтролируемых факторов может входить и время. Неконтролируемые факторы в зависимости от информированности о них подразделяются на три подгруппы:
  

• детерминированные неконтролируемые факторы – неслучайные фиксированные величины, значения которых полностью известны;
  
• стохастические неконтролируемые факторы – случайные величины и процессы с известными законами распределения;
  
• неопределенные неконтролируемые факторы, для каждого из которых известна только область, внутри которой находится закон распределения, значения неопределенных факторов неизвестны в момент принятия решения.
  

Значения контролируемых факторов обычно ограничены рядом естественных причин, например, ограниченностью располагаемых ресурсов. Аналогично могут быть ограничены и области возможных значений неконтролируемых факторов.

Языки описания методов принятия решений

Об одном и том же явлении можно говорить на различных языках различной степени общности и адекватности. К настоящему времени сложились три основных языка описания выбора.

Самым простым, наиболее развитым и наиболее популярным является критериальный язык.

Критериальный язык.

Название этого языка связано с основным предположением, состоящим в том, что каждую отдельно взятую альтернативу можно оценить некоторым конкретным (одним) числом, после чего сравнение альтернатив сводится к сравнению соответствующих им чисел.

Пусть, например, {X} – множество альтернатив, а x – некоторая определенная альтернатива, принадлежащая этому множеству: xX. Тогда считается, что для всех x может быть задана функция q(x), которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности и т.п.), обладающая тем свойством, что если альтернатива x₁ предпочтительнее x₂ (обозначается: x₁ > x₂), то q(x₁)>q(x₂).

При этом выбор сводится к отысканию альтернативы с наибольшим значением критериальной функции.

Однако на практике использование лишь одного критерия для сравнения степени предпочтительности альтернатив оказывается неоправданным упрощением, так как более подробное рассмотрение альтернатив приводит к необходимости оценивать их не по одному, а по многим критериям, которые могут иметь различную природу и качественно отличаться друг от друга.

Например, при выборе наиболее приемлемого для пассажиров и эксплуатирующей организации типа самолета на определенных видах трасс сравнение идет одновременно по многим группам критериев: техническим, технологическим, экономическим, социальным, эргономическим и др.

Многокритериальные задачи не имеют однозначного общего решения. Поэтому предлагается множество способов придать многокритериальной задаче частный вид, допускающий единственное общее решение. Естественно, что для разных способов эти решения являются в общем случае различными. Поэтому едва ли не главное в решении многокритериальной задачи – обоснование данного вида ее постановки.

Используются различные варианты упрощения многокритериальной задачи выбора. Перечислим некоторые из них.

1. Условная максимизация (находится не глобальный экстремум интегрального критерия, а локальный экстремум основного критерия).

2. Поиск альтернативы с заданными свойствами.

3. Нахождение множества Парето.

4. Сведение многокритериальной задачи к однокритериальной путем ввода интегрального критерия.

Рассмотрим подробнее формальную постановку метода сведения многокритериальной задачи к однокритериальной.

Введем интегральный критерий q₀(x), как скалярную функцию векторного аргумента:

q₀(x)= q₀((q₁(x), q₂(x),…, q_n(x)).

Интегральный критерий позволяет упорядочить альтернативы по величине q₀, выделив тем самым наилучшую (в смысле этого критерия). Вид функции q₀ определяется тем, как конкретно мы представляем себе вклад каждого критерия в интегральный критерий. Обычно используют аддитивные и мультипликативные функции:





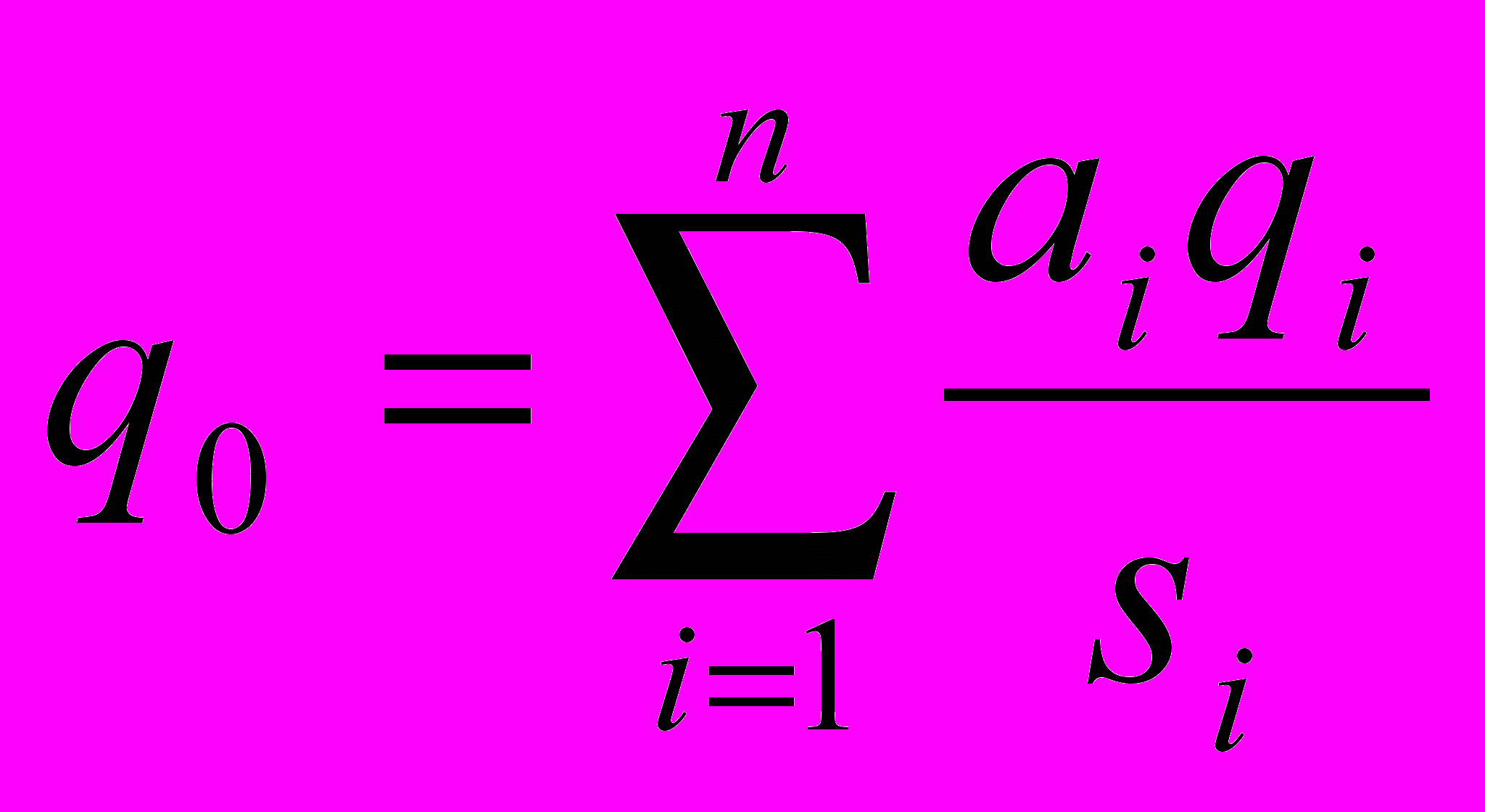
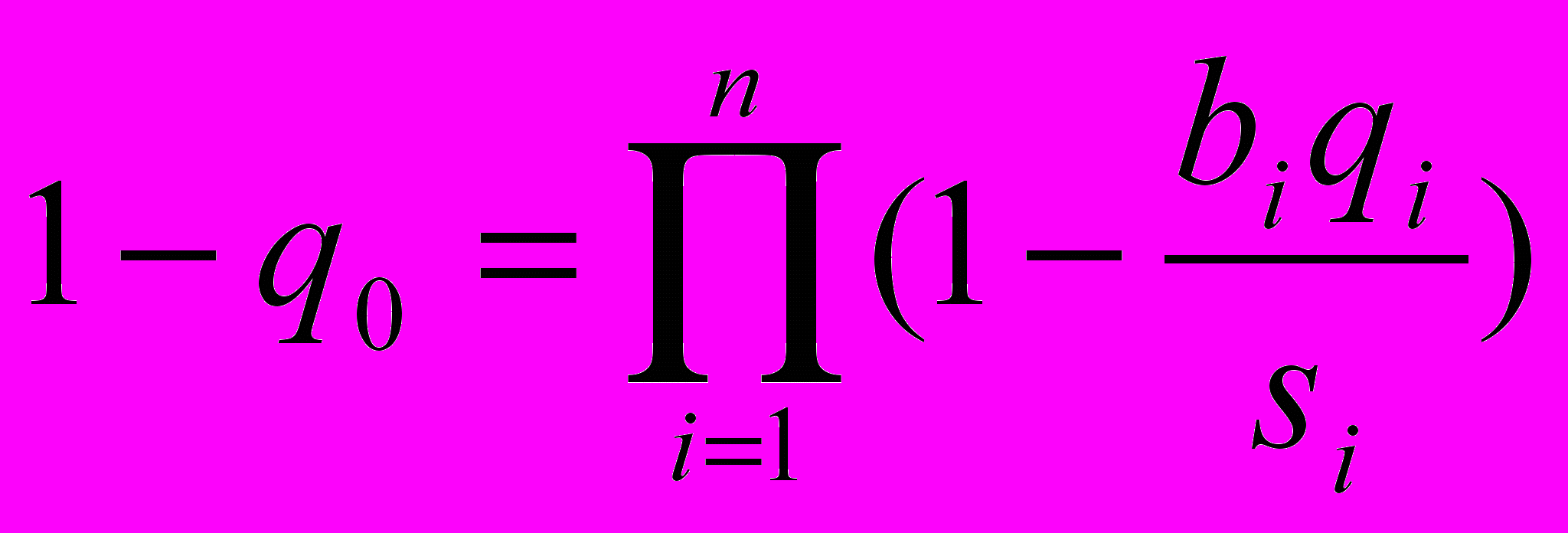
Коэффициенты s_i обеспечивают:

1. Безразмерность или единую размерность числа a_iq_i/s_i (различные частные критерии могут иметь разную размерность, и тогда над ними нельзя производить арифметических операций и свести их в интегральный критерий).

2. Нормировку, т.е. обеспечение условия: b_iq_i/s_i<1.

Коэффициенты a_i и b_i отражают относительный вклад частных критериев q_i в интегральный критерий.

Итак, в многокритериальной постановке задача принятия решения о выборе одной из альтернатив сводится к максимизации интегрального критерия:



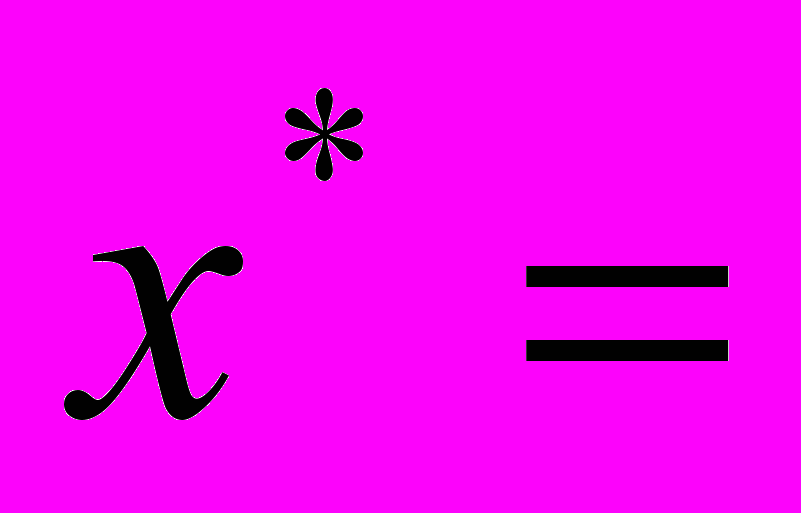
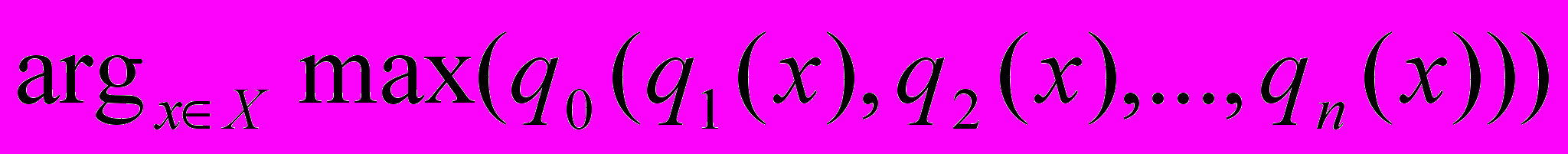
Основная проблема в многокритериальной постановке задачи принятия решений состоит в том, что необходимо найти такой аналитический вид коэффициентов a_i и b_i, который бы обеспечил следующие свойства модели:

• высокую степень адекватности предметной области и точке зрения экспертов;
  
• минимальные вычислительные трудности максимизации интегрального критерия, т.е. его расчета для разных альтернатив;
  
• устойчивость результатов максимизации интегрального критерия от малых возмущений исходных данных.
  

Устойчивость решения означает, что малое изменение исходных данных должно приводить к малому изменению величины интегрального критерия, и, соответственно, к малому изменению принимаемого решения. Таким образом, если исходные данные практически те же, то и решение должно приниматься или тоже самое, или очень близкое.

Язык последовательного бинарного выбора

Язык бинарных отношений является обобщением многокритериального языка и основан на учете того факта, что когда мы даем оценку некоторой альтернативе, то эта оценка всегда является относительной, т.е. явно или чаще неявно в качестве базы или системы отсчета для сравнения используются другие альтернативы из исследуемого множества или из генеральной совокупности. Мышление человека основано на поиске и анализе противоположностей (конструктов), поэтому нам всегда проще выбрать один из двух противоположных вариантов, чем один вариант из большого и никак неупорядоченного их множества.

Таким образом, основные предположения этого языка сводятся к следующему:

• отдельная альтернатива не оценивается, т.е. критериальная функция не вводится;
  
• для каждой пары альтернатив некоторым образом можно установить, что одна из них предпочтительнее другой или они равноценны или несравнимы;
  
• отношение предпочтения в любой паре альтернатив не зависит от остальных альтернатив, предъявленных к выбору.
  

Существуют различные способы задания бинарных отношений: непосредственный, матричный, с использованием графов предпочтений, метод сечений и др.

Отношения между альтернативами одной пары выражают через понятия эквивалентности, порядка и доминирования.

Обобщенный язык функций выбора

Язык функций выбора основан на теории множеств и позволяет оперировать с отображениями множеств на свои подмножества, соответствующие различным вариантам выбора без необходимости перечисления элементов. Этот язык является весьма общим и потенциально позволяет описывать любой выбор. Однако математический аппарат обобщенных функций выбора в настоящее время еще только разрабатывается и проверяется в основном на задачах, которые уже решены с помощью критериального или бинарного подходов.

Методы оценивания в процессе принятия решения

Групповой выбор

Пусть имеется группа лиц, имеющих право принимать участие в коллективном принятии решений. Предположим, что эта группа рассматривает некоторый набор альтернатив, и каждый член группы осуществляет свой выбор. Ставится задача о выработке решения, которое определенным образом согласует индивидуальные выборы и в каком–то смысле выражает "общее мнение" группы, т.е. принимается за групповой выбор.

Естественно, различным принципам согласования индивидуальных решений будут соответствовать различные групповые решения.

Правила согласования индивидуальных решений при групповом выборе называются правилами голосования. Наиболее распространенным является "правило большинства", при котором за групповое решение принимается альтернатива, получившая наибольшее число голосов.

Необходимо понимать, что такое решение отражает лишь распространенность различных точек зрения в группе, а не действительно оптимальный вариант, за который вообще никто может и не проголосовать. "Истина не определяется путем голосования".

Кроме того, существуют так называемые "парадоксы голосования", наиболее известный из которых парадокс Эрроу.

Эти парадоксы могут привести, и иногда действительно приводят, к очень неприятным особенностям процедуры голосования: например, бывают случаи, когда группа вообще не может принять единственного решения (нет кворума или каждый голосует за свой уникальный вариант и т.д.), а иногда (при многоступенчатом голосовании) меньшинство может навязать свою волю большинству.

Выбор в условиях неопределенности

Постановка задачи

Большинство реальных инженерных задач содержит в том или ином виде неопределенность. Можно даже утверждать, что решение задач с учетом разного вида неопределенностей является общим случаем, а принятие решений без их учета - частным. Однако, из-за концептуальных и методических трудностей в настоящее время не существует единого методологического подхода к решению таких задач. Тем не менее, накоплено достаточно большое число методов формализации постановки и принятия решений с учетом неопределенностей. При использовании этих методов следует иметь в виду, что все они носят рекомендательный характер и выбор окончательного решения всегда остается за человеком, который является лицом принимающим решение (ЛПР).

При решении конкретных задач с учетом неопределенностей инженер сталкивается с разными их типами. В исследовании операций принято различать три типа неопределенностей:

• неопределенность целей;
  
• неопределенность наших знаний об окружающей обстановке и действующих в данном явлении факторах (неопределенность природы);
  
• неопределенность действий активного или пассивного партнера или противника.
  

В приведенной выше классификации тип неопределенностей рассматривается с позиций того или иного элемента математической модели. Так, например, неопределенность целей отражается при постановке задачи на выборе либо отдельных критериев, либо всего вектора полезного эффекта.

С другой стороны, два другие типа неопределенностей влияют, в основном, на составление целевой функции уравнений ограничений и метода принятия решения. Конечно, приведенное выше утверждение является достаточно условным, как, впрочем, и любая классификация.

Кроме рассмотренной выше классификации неопределенностей надо учитывать их тип (или "род") с точки зрения отношения к случайности.

По этому признаку можно различать стохастическую (вероятностную) неопределенность, когда неизвестные факторы статистически устойчивы и поэтому представляют собой обычные объекты теории вероятностей - случайные величины (или случайные функции, события и т.д.). При этом должны быть известны или определены при постановке задачи все необходимые статистический характеристики (законы распределения и их параметры).

Примером таких задач могут быть, в частности, система технического обслуживания и ремонта любого вида техники, система организации рубок ухода и т.д.

Другим крайним случаем может быть неопределенность нестохастического вида, при которой никаких предположений о стохастической устойчивости не существует. Наконец, можно говорить о промежуточном типе неопределенности, когда решение принимается на основании каких-либо гипотез о законах распределения случайных величин. При этом ЛПР должен иметь в виду опасность несовпадения его результатов с реальными условиями. Эта опасность несовпадения формализуется с помощью коэффициентов риска.

Принятие решений в условиях риска

В некоторых случаях неопределенность знаний является как бы "неполной" и дополняется некоторыми сведениями о действующих факторах, в частности, знанием законов распределения описывающих их случайных величин. Этот промежуточный случай соответствует ситуации риска. Принятие решений в условиях риска может быть основано на одном из следующих критериев:

• критерий ожидаемого значения;
  
• комбинации ожидаемого значения и дисперсии;
  
• известного предельного уровня;
  
• наиболее вероятного события в будущем.
  

Рассмотрим более подробно применение этих критериев.

Критерий ожидаемого значения (КОЗ).

Использование КОЗ предполагает принятие решения, обуславливающего максимальную прибыль при имеющихся исходных данных о вероятности полученного результата при том или другом решении. По существу, КОЗ представляет собой выборочные средние значения случайной величины. Естественно, что достоверность получаемого решения при этом будет зависеть от объема выборки. Так, если обозначить


КОЗ - Е(x1, x2,..., xn), (6.1)

где

x1, x2,..., xn - принимаемые решения при их количестве, равном n, то

E(xi) (r) M(xi), (6.2)

где

M(xi) - математическое ожидание критерия.


Таким образом, КОЗ может применяться, когда однотипные решения в сходных ситуациях приходится принимать большое число раз.


Приведем пример использования этого критерия для принятия решения.

Критерий "ожидаемого значения - дисперсия".

Как указывалось выше, КОЗ имеет область применения, ограниченную значительным числом однотипных решений, принимаемых в аналогичных ситуациях. Этот недостаток можно устранить, если применять комбинацию КОЗ и выборочной дисперсии s2. Возможным критерием при этом является минимум выражения


E(Z, s ) = E(Z) ± kЧ U(z), (6.5)

где

E(Z, s ) - критерий "ожидаемого значения - дисперсия";

k - постоянный коэффициент;

U(Z) = mZ/S - выборочный коэффициент вариации;

mZ - оценка математического ожидания;

S - оценка среднего квадратического ожидания.

Знак "минус" ставится в случае оценки прибыли, знак "плюс" - в случае затрат.


Из зависимости (6.5) видно, что в данном случае точность предсказания результата повышается за счет учета возможного разброса значений E(Z), то есть введения своеобразной "страховки". При этом степень учета этой страховки регулируется коэффициентом k, который как бы управляет степенью учета возможных отклонений. Так, например, если для ЛПР имеет большое значение ожидаемые потери прибыли, то k>>1 и при этом существенно увеличивается роль отклонений от ожидаемого значения прибыли E(Z) за счет дисперсии.

Критерий предельного уровня.

Этот критерий не имеет четко выраженной математической формулировки и основан в значительной степени на интуиции и опыте ЛПР. При этом ЛПР на основании субъективных соображений определяет наиболее приемлемый способ действий. Критерий предельного уровня обычно не используется, когда нет полного представления о множестве возможных альтернатив. Учет ситуации риска при этом может производиться за счет введения законов распределений случайных факторов для известных альтернатив.

Несмотря на отсутствие формализации критерием предельного уровня пользуются довольно часто, задаваясь их значениями на основании экспертных или опытных данных.

Критерий наиболее вероятного исхода.

Этот критерий предполагает замену случайной ситуации детерминированной путем замены случайной величины прибыли (или затрат) единственным значением, имеющим наибольшую вероятность реализации. Использование данного критерия, также как и в предыдущем случае в значительной степени опирается на опыт и интуицию. При этом необходимо учитывать два обстоятельства, затрудняющие применение этого критерия:

• критерий нельзя использовать, если наибольшая вероятность события недопустимо мала;
  
• применение критерия невозможно, если несколько значений вероятностей возможного исхода равны между собой.
  

Учет неопределенных факторов, заданных законом распределения.

Случай, когда неопределенные факторы заданы распределением, соответствует ситуации риска. Этот случай может учитываться двумя путями. Первый - анализом адаптивных возможностей, позволяющих реагировать на конкретные исходы; второй - методически, при сопоставлении эффективности технических решений. Суть первого подхода заключается в том, что законы распределения отдельных параметров на этапе проектирования могут быть определены с достаточной степенью приближения на основе сопоставления с аналогами, из физических соображений или на базе статистических данных и данных прогнозов.

Методический учет случайных факторов, заданных распределением, может быть выполнен двумя приемами: заменой случайных параметров их математическими ожиданиями (сведением стохастической задачи к детерминированной) и "взвешиванием" показателя качества по вероятности (этот прием иногда называют "оптимизация в среднем").

Первый прием предусматривает определение математического ожидания случайной величины v - M(v) и определение зависимости W(M(v)), которая в дальнейшем оптимизируется по u. Однако сведение к детерминированной схеме может быть осуществлено в тех случаях, когда диапазон изменения параметра u невелик или когда зависимость W(u) линейна или близка к ней.

Второй прием предусматривает определение W в соответствии с зависимостями соответственно для дискретных и непрерывных величин:


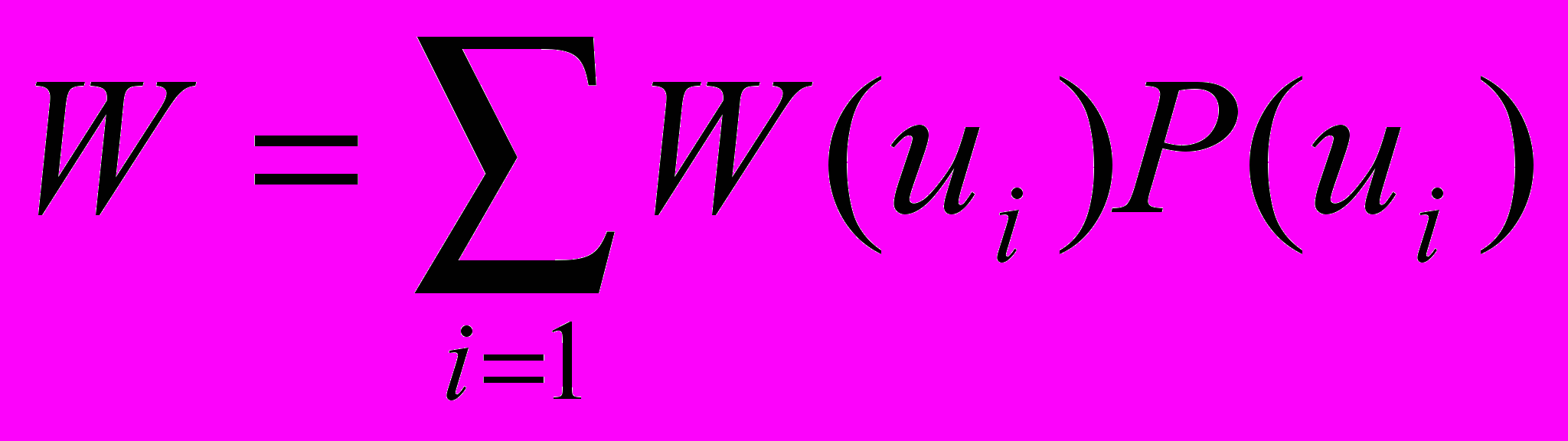; (6.6)


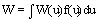, (6.7)


где

P(ui) - ряд распределений случайной величины ui;

f(ui) - плотность распределения случайной величины u.


При описании дискретных случайных величин наиболее часто используют распределения Пуассона, биноминальное. Для непрерывных величин основными распределениями являются нормальное, равномерное и экспоненциальное.

Постановка задачи стохастического программирования

При перспективном и оперативном планировании работы предприятия возникает необходимость в учете ряда случайных факторов, существенно влияющих на процесс производства. К таким факторам относятся спрос, который не всегда может быть предсказуем, непредусмотренные сбои в поступлении сырья, энергии, рабочей силы, неисправности и аварии оборудования. Еще больше случайных факторов необходимо учитывать при планировании производства, эффективность которого зависит от климатических условий, урожайности и т.д. Поэтому, например, задачи планирования лесного производства целесообразно ставить и исследовать в терминах и понятиях стохастического программирования, когда элементы задачи линейного программирования (матрица коэффициентов A, вектора ресурсов b, вектора оценок c) часто оказываются случайными. Подобного типа задачи ЛП принято классифицировать как задачи стохастического программирования (СП).

Подходы к постановке и анализу стохастических задач существенно различаются в зависимости от последовательности получения информации - в один прием или по частям. При построении стохастической модели важно также знать, необходимо ли принять единственное решение, не подлежащее корректировке, или можно по мере накопления информации один или несколько раз корректировать решение. В соответствии с этим в стохастическом программировании исследуются одноэтапные, двухэтапные и многоэтапные задачи.

В одноэтапных задачах решение принимается один раз и не корректируется. Они различаются по показателям качества решения (по целевым функциям), по характеру ограничений и по виду решения.

Задача СП может быть сформулирована в M- и P- постановках по отношению к записи целевой функции и ограничений.

Случайны элементы вектора с (целевая функция).

При M-постановке целевая функция W записывается в виде


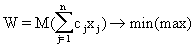, (6.8)


что означает оптимизацию математического ожидания целевой функции. От математического ожидания целевой функции можно перейти к математическому ожиданию случайной величины cj


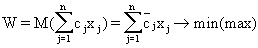. (6.9)


При P- постановке имеем:

• при максимизации
  

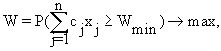(6.10)


где

Wmin - предварительно заданное допустимое наихудшее (минимальное) значение целевой функции.

• при минимизации
  

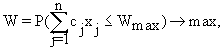(6.11)


где

Wmax - предварительно заданное допустимое наихудшее (максимальное) значение целевой функции.

Суть P-постановки заключается в том, что необходимо найти такие значения xj, при которых максимизируется вероятность того, что целевая функция будет не хуже предельно допустимого значения.

Ограничения задачи, которые должны выполняться при всех реализациях параметров условий задачи, называются жесткими ограничениями. Часто возникают ситуации, в которых постановка задачи позволяет заменить жесткие ограничения их усреднением по распределению случайных параметров. Такие ограничения называют статистическими:


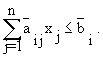(6.12)


В тех случаях, когда по содержательным соображениям можно допустить, чтобы невязки в условиях не превышали заданных с вероятностями, небольшими a i>0, говорят о стохастических задачах с вероятностными ограничениями:


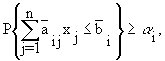(6.13)


т.е. вероятность выполнения каждого заданного ограничения должна быть не менее назначенной величины a i. Параметры a i предполагаются заданными или являются решениями задачи более высокого уровня.

Представленные задачи как в M-, так и в P- постановках непосредственно решены быть не могут. Возможным методом решения этих задач является переход к их детерминированным эквивалентам. В основе этого перехода лежит использование закона распределения случайной величины. В инженерной практике наиболее часто используется нормальный закон распределения, поэтому дальнейшие зависимости приведем для этого случая.

Принимаем, что aij, bi, cj подчинены нормальному закону распределения. В этом случае будет справедлива следующие детерминированные постановки:

• P - постановка целевой функции, максимизация:
  

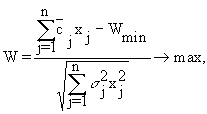(6.14)


Где


и 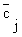s j - математическое ожидание и среднее квадратическое отклонение случайной величины cj.

• P - постановка целевой функции, минимизация:
  

(
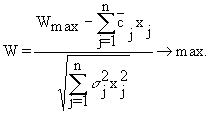
6.15)

• Вероятностные ограничения:
  

г
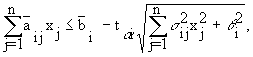
де


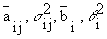- соответственно, математические ожидания и дисперсии случайных величин aij и bi;


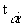- значение центрированной нормированной случайной величины в нормальном законе распределения, соответствующей заданному уровню вероятности соблюдения ограничений a i.

Сделаем несколько замечаний к приведенным зависимостям:

• задача стохастического программирования сведена к задаче нелинейной оптимизации и может быть решена одним из рассматриваемых ранее методов;
  
• сравнение ограничения ресурса в стохастическом программировании и аналогичным ограничением в задаче линейного программирования показывает, что учет случайного характера величин aij и bi приводит к уменьшению располагаемого ресурса на величину
  

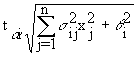, (6.16)


т.е. к необходимости в дополнительном ресурсе. Однако этот дополнительный ресурс может оказаться неиспользованным, но для гарантированного выполнения плана его иметь необходимо.

Метод статистического моделирования

Приведенные формулы (6.6) и (6.7) могут быть использованы для систем независимых случайных величин. Однако для технических систем, как правило, случайные параметры являются зависимыми. Причем эта зависимость не функциональная, а корреляционная. Поэтому для анализа случайных факторов, заданных распределением, широкое применение нашли теория марковских процессов и метод статистического моделирования (метод Монте-Карло).

В задачах принятия оптимальных решений широкое применение получил метод Монте-Карло. Основными особенностями этого метода, основанного на многократном повторении одного и того же алгоритма для каждой случайной реализации, являются: универсальность (метод не накладывает практически никаких ограничений на исследуемые параметры, на вид законов распределения); простота расчетного алгоритма; необходимость большого числа реализаций для достижения хорошей точности; возможность реализации на его основе процедуры поиска оптимальных параметров проектирования. Отметим основные факторы, определившие применение метода статистического моделирования в задачах исследования качества при проектировании: метод применим для задач, формализация которых другими методами затруднена или даже невозможна; возможно применение этого метода для машинного эксперимента над не созданной в натуре системы, когда натурный эксперимент затруднен, требует больших затрат времени и средств или вообще не допустим по другим соображениям.

Байесовский подход в вероятностных задачах принятия решения

Проблемы, имеющие недостаточный информационный потенциал, обладающие многовариантоностью и неодназначностью, встречаются достаточно часто. Сложность усугубляется тем, что состояние объектов является функцией прошлого, настояшего и будущего состояния. Точное оценивание, например, варианта развития, возможных исходов принятого решения и т.д. невозможно. В исследовании подобного рода проблем применяются вероятностные экспертные оценки.

В теории вероятности принимается, что всякому случайному событию А может быть поставлено в соответствии число Р, заключенное между нулем и единицей и являющееся вероятностью наступления события А.

Всякие случайные события могут быть как несовместимыми, так и независимыми.

Если события А и В соместимы, то вероятность наступления одного из них равна:

Р(А или В)= Р(А)+Р(В)

Если события независимы, вероятность их совместного осуществления равна произведению вероятностей каждого независимого события:

Р(А и В)=Р(А)хР(В)

Возможна ситуация, когда вероятность одного события меняется, если произойдет другое событие – это условная вероятность. Последняя форму примет более общий вид:

Р(А и В)=Р(А)хР(В/А),

где Р(В/А) – вероятность события В при условии, что произойдет событие А.

Вероятность невозможного события равна 0, вероятность достоверного события равна 1. Если А – событие, противоположное событию А, то:

Р(А) + Р(А) = 1

Если некоторое событие В вызывается действием какой-либо из причин А ,А ,...А, то существует формула Байеса, позволяющая вычислить вероятность того, что событие В

было названо причиной А или А , ... или А:

В
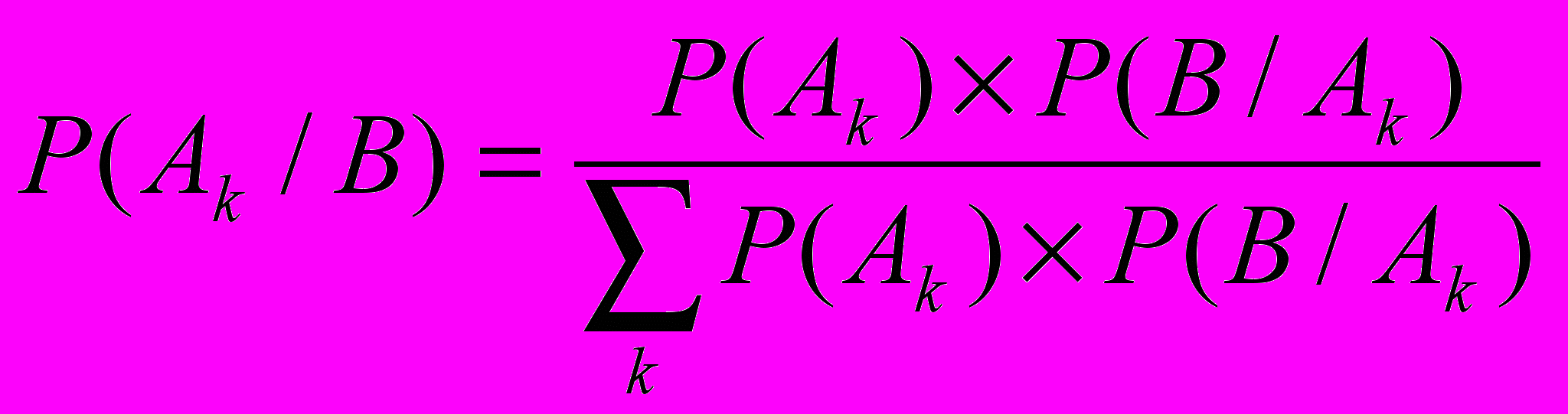
сущности, теории Байеса опираются на предположение, что практически для любого положения имеется, какая бы малая она не была, априорная вероятность того, что данное положение истинно. Эта вероятность может быть быть очень малой, она может оказаться на самом деле нулевой. Если имеется априорная вероятность некоторой гипотезы, то должны иметься некоторые данные, которые могут доказать гипотезу. Если бы их не было, то процесс просто на этом и остановился бы и указанная априорная вероятность осталась неизменной. Однако при наличии относящихся к делу сведений можно модифицировать априорную вероятность так, чтобы получить уже апостериорную вероятность той же самой гиптезы с учетом поступивших новых данных.

Р(Н)- априорная вероятность Н (гипотезы) при отсутствии каких-либо свидетельств;

Р(Н:Е)-апостериорная вероятность Н при наличии свидетельства Е

По определению:

и


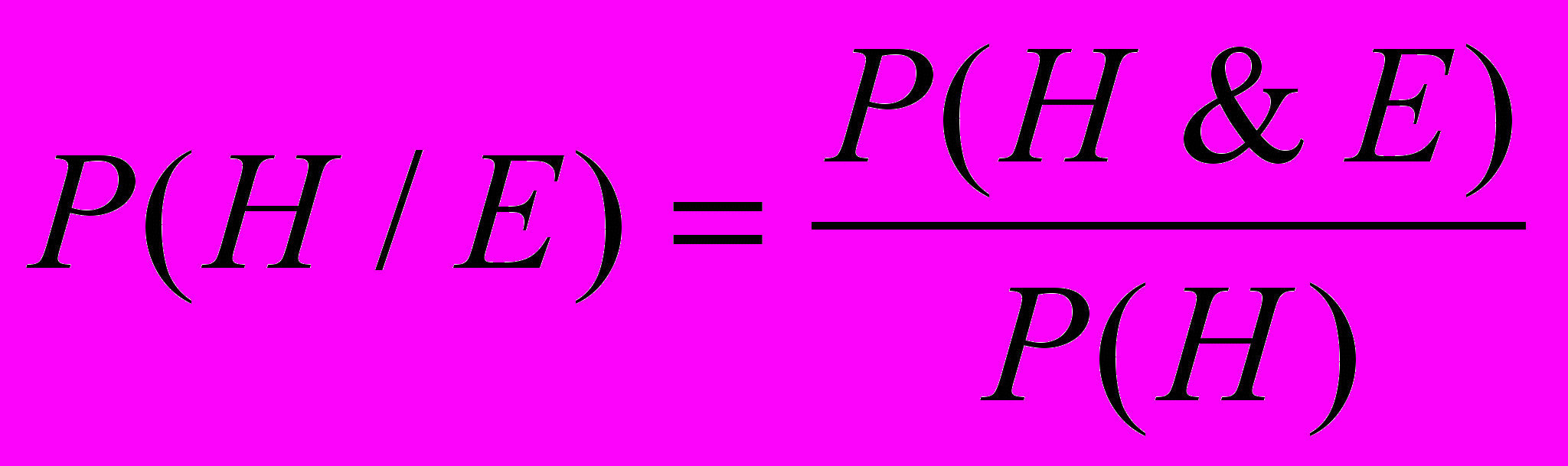
п
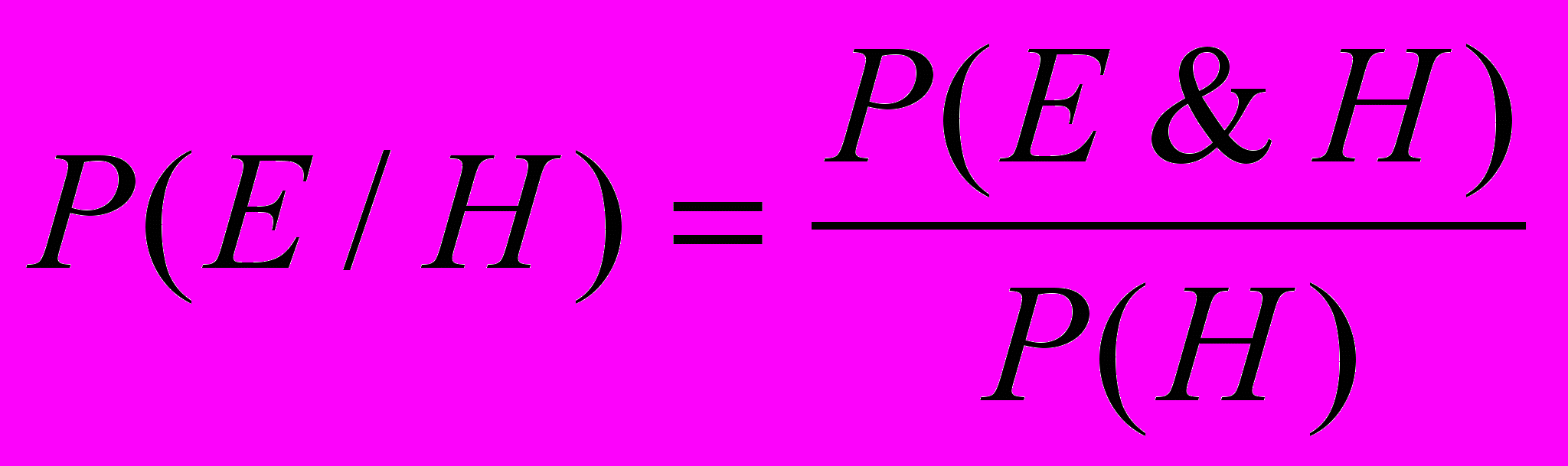
осле некоторой группировки получаем

и


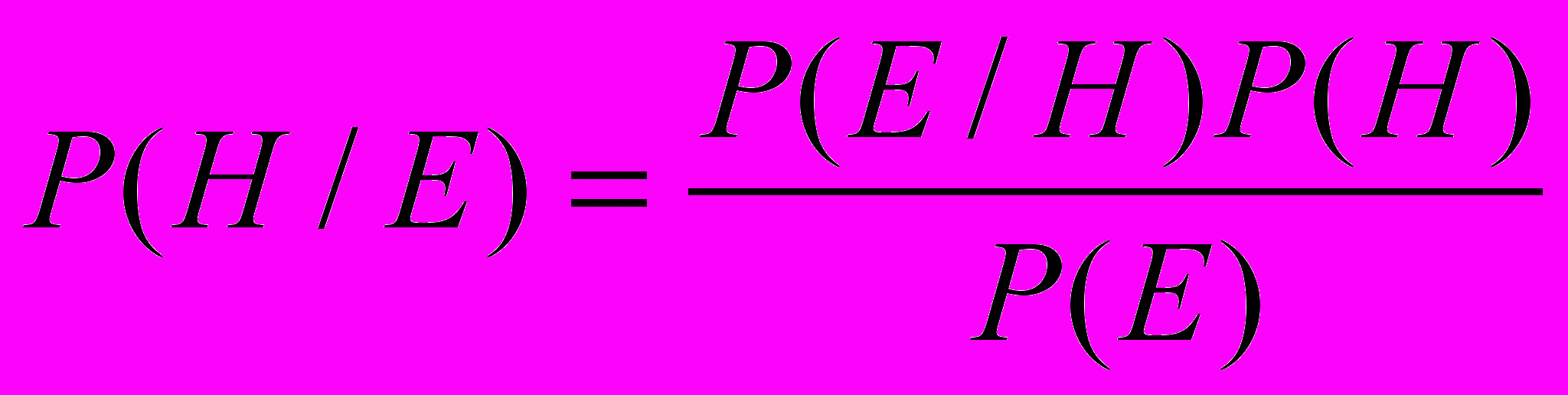
Р(Е)=Р(Е/Н)Р(Н)+Р(Е/не Н)Р(не Н)

Значение Р(Е) является точным, если известно значение Р(Е/не Н), но оно не всегда точно известно. Одна из возможностей обойти это затруднение заключается в использовании общей формулы для вероятности некоторого свидетельства:


Р(Е)= Р(Е/Н )Р(Н )


Каждому элементу свидетельства приписывается цена, отражающая его роль в процессе решения. Цену каждого свидетельства можно вычислить как полную сумму максимальных изменений вероятностей по всем гипотезам.

Т
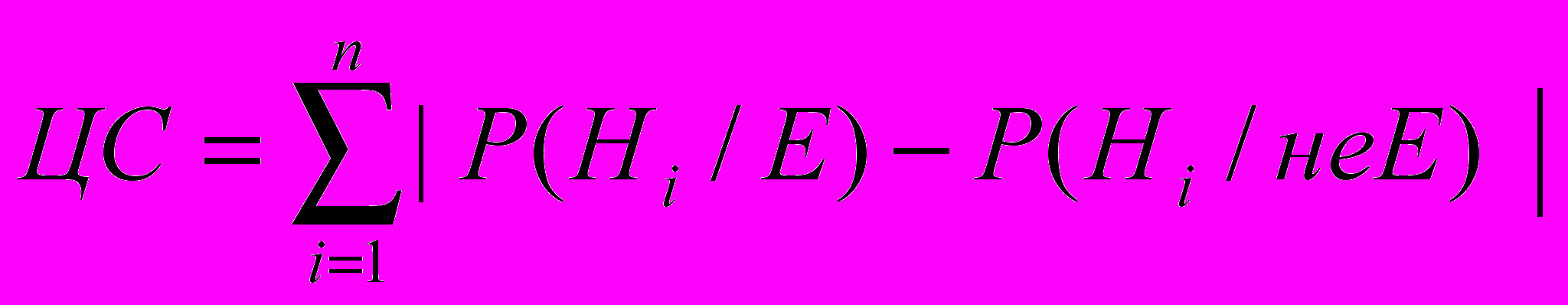
аким образом, цена свидетельства вычисляется для каждого свидетельства Е как сумма максимальных изменений вероятностей, которые могут произойти во всех n гипотезах, к которым это свидетельство приложено.

Цены свидетельств не остаются незменными. По мере того как постоянно уточняются апостериорные вероятности Р(Н /Е), они будут приводить к непрерывному изменению цен свидетельств.

Чем выше цена свидетельства, тем правилнее будет решение.

О некоторых ограничениях оптимизационного подхода

Во всех рассмотренных выше задачах выбора и методах принятия решений проблема состояла в том, чтобы в исходном множестве найти наилучшие в заданных условиях, т.е. оптимальные в определенном смысле альтернативы.

Идея оптимальности является центральной идеей кибернетики и прочно вошла в практику проектирования и эксплуатации технических систем. Вместе с тем эта идея требует осторожного к себе отношения, когда мы пытаемся перенести ее в область управления сложными, большими и слабо детерминированными системами, такими, например, как социально–экономические системы.

Для этого заключения имеются достаточно веские основания. Рассмотрим некоторые из них:

1. Оптимальное решение нередко оказывается неустойчивым, т.е. незначительные изменения в условиях задачи, исходных данных или ограничениях могут привести к выбору существенно отличающихся альтернатив.
   
2. Оптимизационные модели разработаны лишь для узких классов достаточно простых задач, которые не всегда адекватно и системно отражают реальные объекты управления. Чаще всего оптимизационные методы позволяют оптимизировать лишь достаточно простые и хорошо формально описанные подсистемы некоторых больших и сложных систем, т.е. позволяют осуществить лишь локальную оптимизацию. Однако, если каждая подсистема некоторой большой системы будет работать оптимально, то это еще совершенно не означает, что оптимально будет работать и система в целом. Поэтому оптимизация подсистемы совсем не обязательно приводит к такому ее поведению, которое от нее требуется при оптимизации системы в целом. Более того, иногда локальная оптимизация может привести к негативным последствиям для системы в целом. Поэтому при оптимизации подсистем и системы в целом необходимо определить дерево целей и подцелей и их приоритетность.
   
3. Часто максимизация критерия оптимизации согласно некоторой математической модели считается целью оптимизации, однако в действительностью целью является оптимизация объекта управления. Критерии оптимизации и математические модели всегда связаны с целью лишь косвенно, т.е. более или менее адекватно, но всегда приближенно.
   

Итак, идею оптимальности, чрезвычайно плодотворную для систем, поддающихся адекватной математической формализации, на сложные системы необходимо переносить с осторожностью. Конечно, математические модели, которые удается иногда предложить для таких систем, можно оптимизировать. Однако всегда следует учитывать сильную упрощенность этих моделей, которой в случае сложных систем уже нельзя пренебречь, а также то, что степень адекватности этих моделей в случае сложных систем фактически неизвестна. Поэтому не известно, какое чисто практическое значение имеет эта оптимизация. Высокая практичность оптимизации в технических системах не должна порождать иллюзии, что она будет настолько же эффективна и при оптимизации сложных систем. Содержательное математическое моделирование сложных систем является весьма затруднительным, приблизительным и неточным. Чем сложнее система, тем осторожнее следует относиться к идее ее оптимизации.

Поэтому при разработке методов управления сложными, большими слабодетерминированными системами, авторы считают основным не только оптимальность выбранного подхода с формальной математической точки зрения, но и его адекватность поставленной цели и самому характеру объекта управления.

Экспертные методы выбора

При исследовании сложных систем часто возникают проблемы, которые по различным причинам не могут быть строго поставлены и решены с применением разработанного в настоящее время математического аппарата. В этих случаях прибегают к услугам экспертов (системных аналитиков), чей опыт и интуиция помогают уменьшить сложность проблемы.

Однако необходимо учитывать, что эксперты сами представляют собой сверхсложные системы, и их деятельность также зависит от многих внешних и внутренних условий. Поэтому в методиках организации экспертных оценок большое внимание уделяется созданию благоприятных внешних и психологических условий для работы экспертов.

На работу эксперта оказывают влияние следующие факторы:

• ответственность за использование результатов экспертизы;
  
• знание того, что привлекаются и другие эксперты;
  
• наличие информационного контакта между экспертами;
  
• межличностные отношения экспертов (если между ними есть информационный контакт);
  
• личная заинтересованность эксперта в результатах оценки;
  
• личностные качества экспертов (самолюбие, конформизм, воля и др.)
  

Взаимодействие между экспертами может как стимулировать, так и подавлять их деятельность. Поэтому в разных случаях используют различные методы экспертизы, отличающиеся характером взаимодействия экспертов друг с другом: анонимные и открытые опросы и анкетирования, совещания, дискуссии, деловые игры, мозговой штурм и т.д.

Существуют различные методы математической обработки мнений экспертов. Экспертам предлагают оценить различные альтернативы либо одним, либо системой показателей. Кроме того им предлагают оценить степень важности каждого показателя (его "вес" или "вклад"). Самим экспертам также приписывается уровень компетентности, соответствующий вкладу каждого из них в результирующее мнение группы.

Развитой методикой работы с экспертами является метод "Дельфи" . Основная идея этого метода состоит в том, что критика и аргументация благотворно влияют на эксперта, если при этом не затрагивается его самолюбие и обеспечиваются условия, исключающие персональную конфронтацию.

Необходимо особо подчеркнуть, что существует принципиальное различие в характере использования экспертных методов в экспертных системах и в поддержке принятия решений. Если в первом случае от экспертов требуется формализация способов принятия решений, то во втором – лишь само решение, как таковое.

Поскольку эксперты привлекаются для реализации именно тех функций, которые в настоящее время или вообще не обеспечиваются автоматизированными системами, или выполняются ими хуже, чем человеком, то перспективным направлением развития автоматизированных систем является максимальная автоматизация этих функций.

Автоматизированные системы поддержки принятия решений

Человек всегда использовал помощников при принятии решений: это были и просто поставщики информации об объекте управления, и консультанты (советники), предлагающие варианты решений и анализирующие их последствия. Человек, принимающий решения, всегда принимал их в определенном информационном окружении: для военачальника – это штаб, для ректора – ученый совет, для министра – коллегия.

В наше время информационная инфраструктура принятия решений немыслима без автоматизированных систем итерактивной оценки решений и особенно систем поддержки решений (DDS – Decision Support Systems), т.е. автоматизированных систем, которые специально предназначены для подготовки информации, необходимой человеку для принятия решения. Разработка систем поддержки решений ведется, в частности, в рамках интернационального проекта, осуществляемого под эгидой Международного института прикладного системного анализа в Лаксенбурге (Австрия).

Выбор в реальных ситуациях требует выполнения ряда операций, одни из которых более эффективно выполняет человек, а другие – машина. Эффективное объединение их достоинств при одновременной компенсации недостатков и воплощается в автоматизированных системах поддержки принятия решений.

Человек лучше, чем машина принимает решения в условиях неопределенности, но и ему для принятия верного решения необходима адекватная (полная и достоверная) информация, характеризующая предметную область. Однако известно, что человек плохо справляется с большими объемами "сырой" необработанной информации. Поэтому роль машины в поддержке принятия решений может заключаться в том, чтобы осуществить предварительную подготовку информации об объекте управления и неконтролируемых факторах (среде), помочь просмотреть последствия принятия тех или иных решений, а также в том, чтобы представить всю эту информацию в наглядном и удобном для принятия решений виде.

Таким образом, автоматизированные системы поддержки принятия решений компенсируют слабые стороны человека, освобождая его от рутинной предварительной обработки информации, и обеспечивают ему комфортную информационную среду, в которой он может лучше проявить свои сильные стороны. Эти системы ориентированы не на автоматизацию функций лица, принимающего решения (и, как следствие, отчуждение от него этих функций, а значит и ответственности за принятые решения, что часто вообще является неприемлемым), а на предоставлении ему помощи в поиске хорошего решения

Конкретный пример

Предположим, что вы хотите обрабатывать экспертную систему, которая могла бы играть роль вашего личного механика по ремонту автомашин. Это пример очень небольшой базы знаний, рассчитанной на обеспечение советом в области ремонта автомашин с использованием методов, описанных выше:

СЕВШИЙ АККУМУЛЯТОР

0,1; 5; 1; 0; 0,99; 2; 0,7; 0,05; 4; 0,2; 0,5; 5; 0; 0,99; 6,1; 0,01

НЕТ БЕНЗИНА

0,05; 2; 2; 1; 0,01; 6; 0,9; 0,02

ОТСЫРЕЛО ЗАЖИГАНИЕ

0,01; 3; 3; 0,9; 0,1; 4; 0,25; 0,5; 6; 0,9; 0,02

ЗАМАСЛЕНЫ СВЕЧИ

0,01; 2; 4; 0,01; 0,5; 6; 0,9; 0,02

1. ФАРЫ ГОРЯТ, ГОРЯТ ЛИ ФАРЫ?
   
2. УКАЗАТЕЛЬ БЕНЗИНА НА НУЛЕ, НЕ ПОКАЗЫВАЕТ ЛИ ПРИБОР УРОВНЯ БЕНЗИНА СЛИШКОМ МАЛОЕ ЗНАЧЕНИЕ?
   
3. АВТОМАШИНА ОТСЫРЕЛА, НЕ СТОЯЛА ЛИ АВТОМАШИНА ДОЛГО ПОД ДОЖДЕМ?
   

4. АВТОМАШИНА НЕДАВНО ПРОШЛА ТЕХОБСЛУЖИВАНИЕ, ПРОХОДИЛА ЛИ НЕДАВНО ЭТА АВТОМАШИНА ТЕХОБСЛУЖИВАНИЕ?
   
5. СТАРТЕР ПРОВОРАЧИВАЕТСЯ, ПРОВОРАЧИВАЕТСЯ ЛИ СТАРТЕР АВТОМАШИНЫ?
   
6. АВТОМАШИНА НЕ ЗАВОДИТСЯ, АВТОМАШИНА НЕ ЗАВЕДЕТСЯ?
   

Здесь первая группа элементов - это гипотеза, например гипотеза, что батарея села. Вторая группа содержит свидетельства, например информацию о том, что фары горят.

Поскольку я не считаю себя прекрасным механиком, то приводимые мною вероятности могут несколько отклоняться от истинных значений, но, не обращая на это внимание, рассмотрим первую гипотезу о том, что сел аккумулятор. Априорную вероятность того, что на любой данной автомашине сел аккумулятор, возьмем, скажем, равной 0,1, т. е. считается, что в норме у каждой десятой автомашины севший аккумулятор.

Мы прикинули, что имеется пять различных свидетельств, которые могут быть использованы для того, чтобы установить, исправна или нет аккумуляторная батарея на данной автомашине. Первое свидетельство идет под номером 1 (фары горят). Если батарея села, то вероятность наблюдения, что фары горят, равна нулю. С другой стороны если батарея исправна, то Р(Е : не Н) - вероятность того, что фары горят, равна, скажем, 0,99 (т. е. почти наверняка фары будут работать, если не считать той возможное та, что перегорела лампочка или сгорел предохранитель).

Второе свидетельство идет под номером 2. Указатель бензина на нуле. Поскольку этот прибор работает на электричестве, то он тоже может иметь отношение к состоя­нию аккумулятора. Правда, это не очень важно, потому что для работы указателя тре­буется очень небольшой ток. Таким образом, мы прикидываем, что вероятность наблюдать низкое показание прибора уровня бензина, если батарея села, равна 0,7, а вероятность низкого показания прибора при исправной батарее равна 0,05. (Низкое показание может быть и по другой причине, например, потому, что нет бензина!) Заметим, что приведенная вероятность соответствует априорной вероятности гипотезы "нет бензина", по­скольку это единственно возможная иная причина того, что указатель бензина близок к нулю. Точно так же можно и дальше просмотреть список приложимых к этой гипо­тезе свидетельств. Если автомашина недавно прошла техобслуживание, то вероятность того, что аккумулятор сел, существенно меньше; это полностью исключено, если стартер проворачивается; автомашина, безусловно, не заведется, если аккумулятор сел (вероятность равна 1), хотя она может не завестись и при исправном аккумуляторе (вероятность, скажем, 0,01).


Таблица 6.1

Свидетельство Цена свидетельства

Фары горят 0,9174

Указатель бензина на нуле 1,4151

Автомашина отсырела 0,0822

Автомашина недавно прошла техобслуживание 0,1376

Стартер проворачивается 0,9174

Автомашина не заводится 2,3807

Следующая гипотеза "нет бензина" зависит от таких свидетельств, как "указатель бензина на нуле" и "автомашина не заводится". Аналогично гипотеза "отсырело зажи­гание" зависит от свидетельств, что "автомашина отсырела", "автомашина недавно про­шла техобслуживание" и "автомашина не заводится". Замасленные свечи определяются такими свидетельствами, как "автомашина недавно прошла техобслуживание" и "автомашина не заводится" (первое говорит против такой возможности, а второе сви­детельствует за нее). Эти вероятности могут быть взяты из опыта или основаны на более строгих соображениях, но окончательное оправдание могут дать хорошие результаты работы всей системы.

Каждый раз при запуске система всегда будет задавать вопрос: "Заводится ли автомашина?" После этого в зависимости от ответа будут уточнены цены свидетельств. 'Но одного взгляда на табл. 6.1 достаточно, чтобы убедиться, что после свидетельства "автомашина не заводится" систему больше всего интересует вопрос о том, показы­вает ли что-то указатель бензина и проворачивается ли стартер, что выглядит вполне разумным.

Для примера, если ответом на вопрос: "Автомашина не заведется?" - было твер­дое "да", то система вычислит заново цены свидетельств (табл. 6.2) .

Так что следующий вопрос будет касаться указателя уровня бензина. Но обратите Внимание, как подскочили значения всех оставшихся цен свидетельств, когда была по­лучена новость, что ваша машина не заводится. Внезапно механик по ремонту автома­шин стал интересоваться тем, что прежде его почти не интересовало.

С другой стороны, если вы ответили "нет" на вопрос: "Автомашина не заведется?" - (т.е. машина в исправности), то значения всех цен свидетельств решительно падают. Наш механик отбрасывает все четыре гипотезы, которые он рассматривал, и приходит к заключению, что с машиной все в порядке, не задавая больше никаких вопросов.

Таблица 6.2

Свидетельство Цена свидетельства

Фары горят 0,9991

Указатель бензина на нуле 1,2135

Автомашина отсырела 0,7554

Автомашина недавно прошла техобслуживание 0,8153

Стартер проворачивается 0,9991

Автомашина не заводится 0

Литература.

1. Экспертные системы. Принципы работы и примеры. Под редакцией Р.Форсайта.