Математический факультет

Вид материала

Документы

Содержание Операторы цикла Вызов подпрограмм.

Подобный материал:

• Клименко Алексей Владимирович Образование 2001-2006: Механико-математический факультет, 41.65kb.
• Программа вступительных испытаний по физике москва, 138.12kb.
• Механико-математический факультет магистратура, 328.27kb.
• Цель образовательной программы углубление, систематизация и обобщение знаний по математике,, 5.89kb.
• П. Г. Демидова Математический факультет. Реферат, 227.26kb.
• Н. П. Огарева математический факультет кафедра дифференциальных уравнений рабочая программа, 200.47kb.
• Г. В. Плеханова Экономико-математический факультет, факультет Информатики Дисциплина:, 80.62kb.
• Математический факультет; математическое обеспечение и администрирование информационных, 394.55kb.
• Утверждаю, 123.18kb.
• Математический факультет, 669.04kb.

Операторы цикла

Часто при решении задач необходимо многократно выполнять определённую последовательность действий. Такие повторяющиеся действия называются циклами. В языке Object Pascal возможна организация 3-х видов циклов.

1. С параметром (оператор for)
   
2. С предусловием (оператор while)
   
3. С постусловием (оператор repeat)
   

Оператор цикла for организует выполнение последовательности операторов заранее известное число раз. Существуют два варианта оператора:

1. С увеличением счётчика:

for <счётчик> := <начальное значение> to <конечное значение> do <оператор>;

2. С уменьшением счётчика:

for <счётчик>:=<начальное значение>downto <конечное значение>do <оператор>;

Здесь

<счётчик> – переменная порядкового типа – параметр цикла;

<начальное значение> и <конечное значение> – выражения, которые должны быть совместимы с параметром цикла;

<оператор> – это оператор, который выполняется в цикле – тело цикла.

Если в цикле необходимо выполнить группу операторов, то её следует заключить в операторные скобки begin…end.

Оператор for действует следующим образом. Вначале вычисляются начальное и конечное значения счётчика. Далее счётчику присваивается начальное значение. Затем значение счётчика сравнивается с конечным значением. Далее, пока счётчик меньше или равен конечному значению ( в первом варианте ) или больше или равен ( во втором варианте ), выполняется очередная итерация цикла. В противном случае происходит выход из цикла. Выполнение очередной итерации включает в себя сначала выполнение тела цикла, а затем присвоение счётчику следующего большего значения (в первом варианте ) или следующего меньшего значения ( во втором варианте ). Если параметр цикла целого типа, то это означает увеличение либо уменьшение его на 1. В первом варианте начальное значение должно быть меньше конечного, а во втором варианте – больше конечного. В противном случае тело цикла не будет выполнено ни разу.

Пример 12. Напечатать столбиком все целые числа от 30 до 45.

var i : integer;

begin

for i:=30 to 45 do writeln(i);

readln

end.


Пример 13. Найти сумму всех целых чисел от 10 до 50.

var i, s : integer;

begin

s:=0;

for i:=10 to 50 do s:=s+i;

writeln(s);

readln

end.

Рассмотрим выполнение этой программы по шагам:

i s

10 0 + 10 = 10

11 10 + 11 = 21

12 21 + 12 = 33

…………………………..

50 1230


Пример 14. Вычислить сумму 2² + 2³ + 2⁴ + … + 2¹⁰

Для решения этой задачи сначала ответим на вопрос: сколько слагаемых в этой сумме? Слагаемые – это степени двойки от 2^ой до 10^ой. Следовательно, имеем 9 слагаемых. Каждое следующее слагаемое получается из предыдущего умножением на 2. Пусть a – очередное слагаемое, s – сумма. Используя эти соображения, запишем решение:

var i, a, s : integer;

begin

a:=2; s:=0;

for i:=1 to 9 do

begin a:=a*2; s:=s+a end;

writeln(s);

readln

end.


Пример 15. Подсчитать количество двузначных чисел, кратных 7.

Решение. Двузначные числа – это все целые числа от 10 до 99. k – счётчик двузначных чисел, кратных 7.

var i, k : integer;

begin

k:=0;

for i:=10 to 99 do

if i mod 7=0 then inc(k);

writeln(k);

readln;

end.


Пример 16. Дано натуральное число n, которое вводится с клавиатуры. Вычислить сумму всех его натуральных делителей, за исключением самого числа.

Решение. Мы будем перебирать все числа от 1 до n div 2 (так как у числа n не может быть натуральных делителей, больших, чем n div 2) и складывать те из них, на которые число n делится без остатка.

var i, s, n : integer;

begin

readln(n);

s:=0;

for i:=1 to n div 2 do

if (n mod i =0) then s:=s+i;

writeln(s);

readln

end.


Пример 17. Дана последовательность из 10 действительных чисел, которые вводятся с клавиатуры. Подсчитать сумму тех из них, которые больше, чем 5,12.

Решение. На каждом из 10 шагов цикла мы должны: во-первых, прочитать очередное число a, во-вторых, если прочитанное число удовлетворяет условию a>5.12, добавить его в сумму.

var i : integer; a, s : real;

begin

s:=0;

for i:=1 to 10 do

begin

read(a);

if a>5.12 then s:=s+a

end;

writeln(s:5:2);

readln; readln

end.

После запуска приложения введём через пробел последовательность чисел

6.5 -0.4 2.01 12.8 -9.2 -0.15 10.7 3.98 -4.1 0.6

и нажмём Enter. Получим результат 30.00.


Пример 18. Дана последовательность из 10 действительных чисел, которые вводятся с клавиатуры. Найти максимальный элемент последовательности.

var i : integer; a, max : real;

begin

read(max);

for i:=2 to 10 do

begin

read(a);

if a>max then max:=a

end;

writeln(max:5:2);

readln; readln

end.

Рассмотрим выполнение этой программы по шагам, считая, что последовательность чисел та же, что и в предыдущем примере:

i a max

6.5

2 -0.4 6.5

3 2.01 6.5

4 12.8 12.8

5 -9.2 12.8

6 -0.15 12.8

………………………………

В результате получим ответ 12.8.


Пример 19. Напечатать все натуральные числа от 1 до 1000, количество делителей каждого из которых равно 5.

Решение. Перебираем все целые числа n от 1 до 1000, и для каждого числа n просматриваем все целые числа i от 1 до n, подсчитывая количество ( k ) делителей числа n. Каждое число n, для которого k=5, выводим на печать.

var i, n : integer; k : byte;

begin

for n:=1 to 1000 do

begin

k:=0;

for i:=1 to n do

if (n mod i = 0) then inc(k);

if k=5 then writeln(n)

end;

readln

end.


Задачи.

46. Найти произведение всех целых чисел от 1 до 10.
    
47. Напечатать столбиком значения sin 0.1 sin 0.2 sin 0.3 … sin 1.1
    
48. Вычислить
    

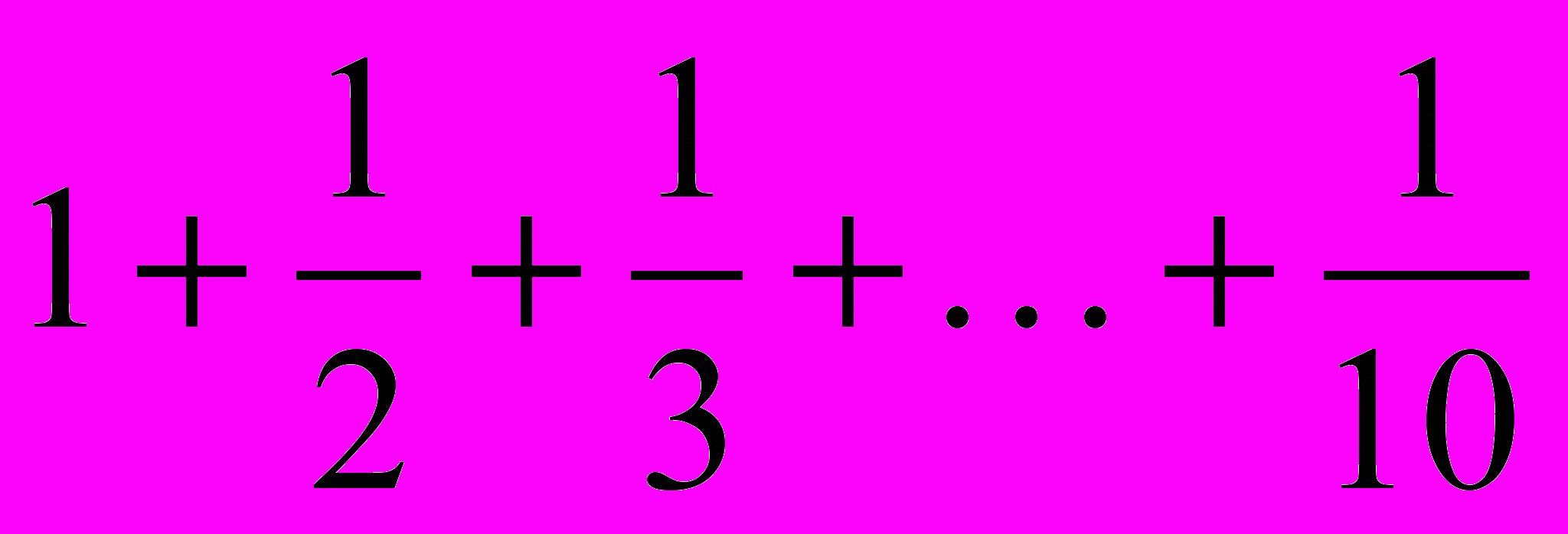
46. Вычислить
    

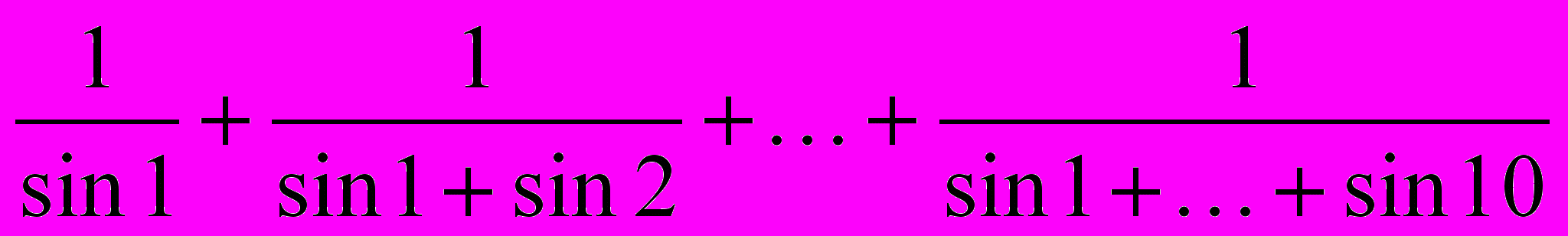
50. Дано натуральное число n. Вычислить значение выражения, в котором n корней:



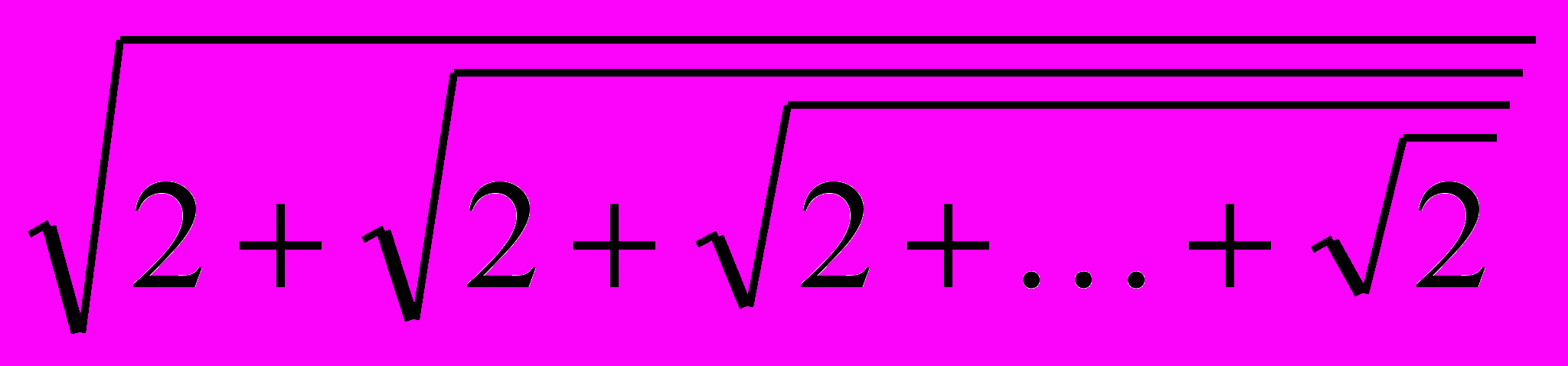
51. Вычислить



52. Дано натуральное число n (n13). Вычислить



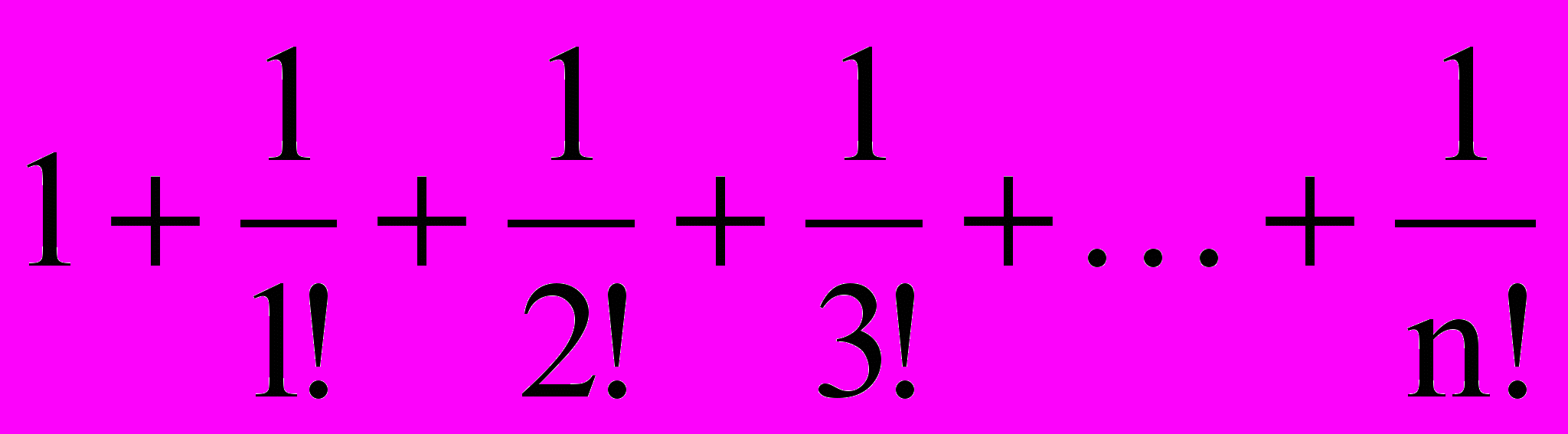
53*. Дано вещественное число x. Вычислить




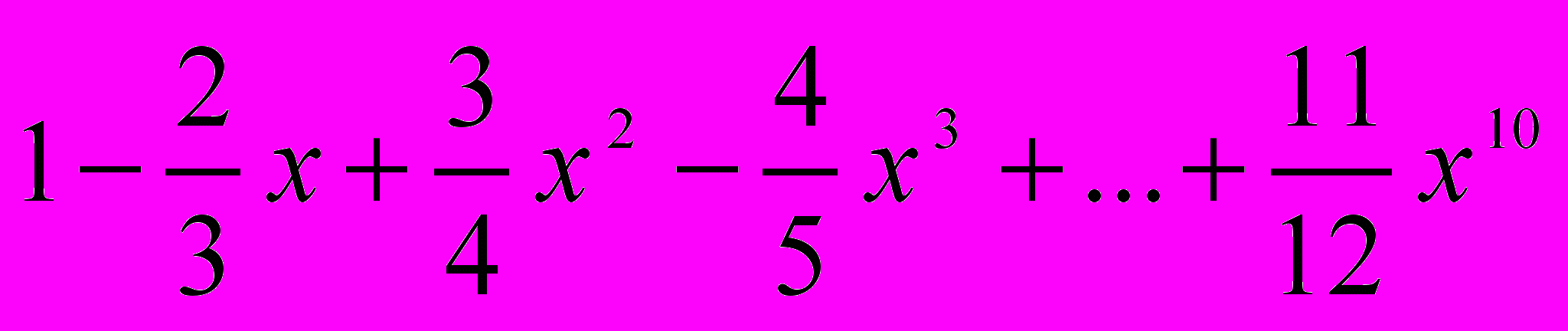
54. Последовательность чисел a₀, a₁, a_2, … образуется по закону a₀1; a_k=ka_k-1+1/k (k  1,2, … ). Дано натуральное число n . Получить a_1, a₂, … ,a_n.

55. Последовательность чисел Фибоначчи f_k образуется так:

f₀=1, f₁=1, f_k = f_k-2 + f_k-1.

Дано натуральное число n . Получить f_n.

56. Найти сумму натуральных чисел из интервала от 10 до 80, которые содержат цифру 2.

57. Найти все двузначные числа, которые кратны 4 и у которых сумма цифр также кратна 4.

58. Определить количество натуральных чисел из интервала от 100 до 500, сумма цифр которых равна 15.

59. Найти все такие двузначные числа, что если к сумме цифр этого числа прибавить квадрат этой суммы, то получится это число.
    

60. Найти все трёхзначные числа, которые при делении на 2 дают остаток 1, при делении на 3  остаток 2, при делении на 4  остаток 3, а само число делится на 5.

61. Найти четырёхзначное число, которое при делении на 133 даёт в остатке 125, а при делении на 134 даёт в остатке 111.

62. Квадрат трёхзначного числа оканчивается тремя цифрами, которые как раз и составляют это число. Найти все такие трёхзначные числа.

63. В трёхзначном числе зачеркнули первую цифру слева. Когда полученное двузначное число умножили на 7, то получили данное число. Найти это трёхзначное число.

64. Дано натуральное число n. Вычислить количество его нечётных делителей.

65. Дано натуральное число n. Проверить, верно ли, что сумма его делителей, за исключением самого числа, равна n.

66. Дана последовательность из 10 действительных чисел, которые вводятся с клавиатуры. Подсчитать произведение отрицательных элементов последовательности.

67. Дана последовательность из 10 действительных чисел, которые вводятся с клавиатуры. Найти среднее арифметическое положительных элементов последовательности.

68. Дана последовательность из 10 действительных чисел, которые вводятся с клавиатуры. Сколько раз в этой последовательности меняется знак ? (Например, в последовательности 10 -4 12 56 -23 знак меняется 3 раза)

69. Дана последовательность из 10 действительных чисел, которые вводятся с клавиатуры. Найти минимальный элемент последовательности и его номер.

70. Дана последовательность из 10 действительных чисел, которые вводятся с клавиатуры. Найти разность между максимальным и минимальным элементами последовательности.

71*. Дана последовательность из 10 действительных чисел, которые вводятся с клавиатуры. Найти порядковый номер того из них, которое наиболее близко к какому-нибудь целому числу.

72*. Даны n различных отрезков на прямой, каждый из которых задан парой действительных чисел (a,b), являющихся координатами концов отрезка. Определить координаты концов отрезка, являющегося пересечением всех этих отрезков. Если такого отрезка нет, то сообщить об этом.

73*. Даны n различных точек на плоскости, каждая из которых задана своими координатами (x,y). Определить радиус наименьшего круга (с центром в начале координат), в который попадают все эти точки.

74. Найти натуральное число от 1 до 1000 с максимальной суммой делителей.

75. Число называется совершенным, если оно равно сумме всех своих делителей, кроме самого этого числа. (Например, 28124714). Получить все совершенные числа из интервала от 1 до 10000.


Оператор цикла с предусловием WHILE имеет следующий формат:

while <логическое выражение> do <оператор>;

Выполняется оператор следующим образом. Вначале вычисляется значение логического выражения. Если это значение равняется true, то выполняется тело цикла – оператор, стоящий после слова do. После этого снова вычисляется значение логического выражения и процесс повторяется. Цикл прекращается, если при очередном вычислении логического выражения его значение окажется равным false. Если при первом вычислении значения логического выражения окажется, что оно равно false, то тело цикла не выполнится ни разу. В качестве оператора тела цикла может быть использован составной оператор, заключённый в операторные скобки begin .. end.

Пример 20. Дано натуральное число n ( n0 ). Подсчитать количество цифр данного числа.

var n : longint; k : byte;

begin

readln(n); k0;

while n0 do

begin inc(k); nn div 10 end;

writeln(k);

readln

end.


Пример 21. Даны действительные числа a₁, a₂, a₃, … . Известно, что a₁>0 и что среди a₂ ,a_{3 . . .} есть хотя бы одно отрицательное число. Пусть a₁, a₂, … , a_n  элементы данной последовательности, предшествующие первому отрицательному элементу (n заранее неизвестно). Получить a₁ + a₂ + … + a_n .

var a, s : real;

begin

s:=0; read(a);

while a>=0 do

begin

s:=s + a; read(a)

end;

writeln(s:6:1);

readln; readln

end.


Пример 22. Дано 10 натуральных чисел. Проверить, что среди них есть хотя бы одно, кратное 3.

const n = 10;

var t : boolean; x, i : integer;

begin

t:=true; i:=0;

while t and (i
begin read(x); inc(i); t:=x mod 3<>0 end;

writeln( not(t) );

readln; readln

end.


Пример 23. Даны натуральные числа n и m. Получить все натуральные числа из диапазона от m до n, сумма цифр которых равна 12.

var i, n, m, s, a : integer;

begin

readln(m, n);

for i:=m to n do

begin

s:=0; a:=i;

while a<>0 do

begin s:=s + a mod 10; a:=a div 10 end;

if s=12 then writeln(i);

end;

readln;

end.


Задачи.

76. Дано натуральное число n . Найти сумму цифр этого числа.

77. Дано натуральное число n . Поменять порядок цифр числа на обратный.

78. Дано натуральное число n . Найти самую большую его цифру.

79. Дано натуральное число n . Приписать 1 в начало и в конец записи числа n . ( 3456  134561 ).

80. Дано натуральное число n . Поменять местами первую и последнюю цифры числа n .

81. Дано натуральное число n . Выяснить, входит ли цифра 7 в запись числа n² .

82. Даны действительные числа a₁, a₂, a₃, … . Известно, что a₁>0 и что среди a₂ ,a_{3 . . .} есть хотя бы одно отрицательное число. Пусть a₁, a₂, … , a_n  элементы данной последовательности, предшествующие первому отрицательному элементу (n заранее неизвестно). Получить:

1. a₁  a₂  a₃  . . . a_n ;
   
2. среднее арифметическое a₁, a₂, … a_n ;
   
3. a₁, a₁a₂, a₁a₂a₃, … , a₁a₂ … a_n ;
   
4. a₁ + 2a₂ + 2a₃ + … +2a_n-1 + a_n ;
   
5. a₁a₂ + a₂a₃ + … + a_n-1a_n + a_na₁ ;
   
6. n + a_n ;
   
7. a₁  a_n  .
   

83. Дано 10 вещественных чисел. Верно ли, что в этой последовательности нет отрицательных элементов.

84. Дана последовательность из 10 целых чисел. Определить, со скольких отрицательных она начинается.

85. Дано 10 вещественных чисел. Определить, образуют ли они возрастающую последовательность.

86. Дано 10 вещественных чисел. Верно ли, что в этой последовательности есть хотя бы одна пара рядом стоящих нулей.

87. Даны натуральные числа n и m. Подсчитать количество чисел из диапазона от m до n, у которых первая и последняя цифры одинаковые.

88*. Даны натуральные числа n и m. Подсчитать количество чисел из диапазона от m до n, в записи которых есть цифра 0.

89*. Даны натуральные числа a и b (ab). Получить все простые числа p, удовлетворяющие неравенствам apb.


Оператор цикла с постусловием REPEAT имеет следующий формат:

repeat <оператор> until <логическое выражение>;

Выполняется оператор repeat следующим образом. В начале выполняется оператор тела цикла. Затем вычисляется значение логического выражения. Если оно равняется false, то выполняется следующая итерация цикла. В противном случае цикл прекращается. Задача о вычислении количества цифр данного натурального числа n может быть решена с помощью оператора цикла с постусловием следующим образом:

Пример 24.

var n : longint; k : byte;

begin

readln(n); k0;

repeat inc(k); nn div 10 until n0;

writeln(k);

readln

end.

Тело цикла оператора цикла с постусловием можно не заключать в операторные скобки, так как их роль здесь выполняют слова repeat until .

Пример 25.

Алгоритм Евклида – алгоритм нахождения НОД двух натуральных чисел. Алгоритм основан на следующем свойстве. Пусть x, y – натуральные числа, одновременно не равные нулю, и пусть x>y. Тогда, если y=0, то НОД(x,y)=x, а если y0, то НОД(x,y) = НОД(y,r), где r = x mod y. Программа, реализующая алгоритм Евклида с использованием оператора repeat until:

var x, y, nod : integer;

begin

readln(x, y);

repeat

if x>y then x:=x mod y

else y:=y mod x

until (x=0) or (y=0);

nod:=x + y;

writeln(nod);

readln

end.

Пусть x=48 y=18. Рассмотрим выполнение этой программы по шагам:

x=48 y=18

x>y x=48 mod 18=12 y=18

y>x x=12 y=18 mod 12=6

x>y x=12 mod 6=0 y=6

nod = 0 + 6 = 6

Пусть x=21 y=16.

x=21 y=16

x>y x=21 mod 16=5 y=16

y>x x=5 y=16 mod 5=1

x>y x=5 mod 1=0 y=1

nod = 0 + 1 = 1


Задачи.

90. Найти НОД трёх натуральных чисел. Указание:

НОД(x,y,z)=НОД( НОД(x,y), z ).

91. Даны натуральные числа m и n. Найти такие натуральные числа p и q, не имеющие общих делителей, что



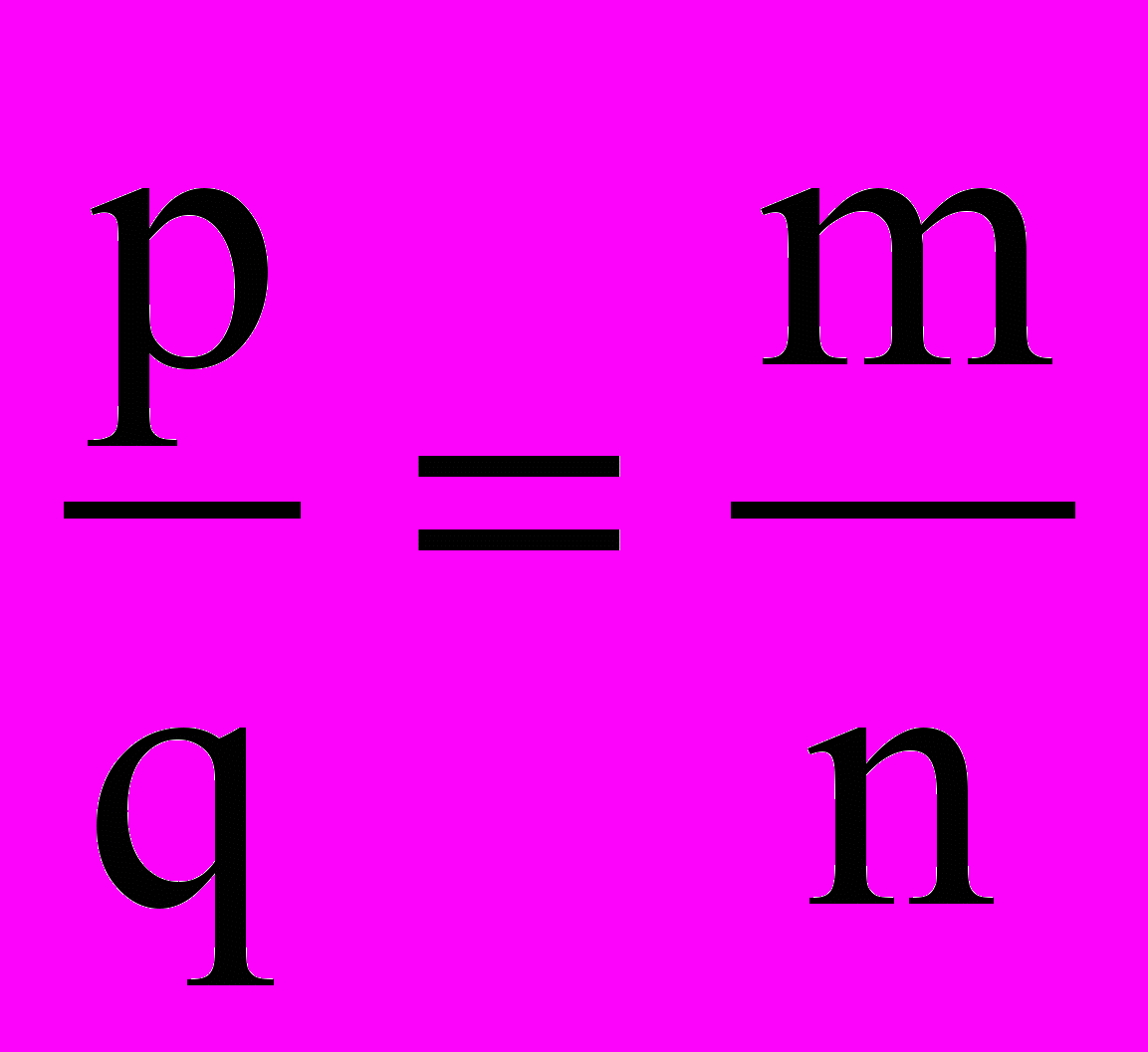
92. Найти первое число Фибоначчи, большее заданного целого числа m (m1).

93. Вычислить S  сумму всех чисел Фибоначчи, которые не превосходят 1000.

94. Дано целое число m (m1). Получить наибольшее целое k , при котором 4^k  m.

95. Дано натуральное число n . Получить наименьшее число вида 2^r , превосходящее n.


1.4 Процедуры и функции.

Если в программе возникает необходимость частого обращения к некоторой группе операторов, то рационально выделить такую группу операторов в самостоятельный блок, к которому можно обращаться, указывая его имя. Такие разработанные программистом блоки называются подпрограммами пользователя. В языке Паскаль механизм подпрограмм реализуется в виде процедур и функций.


Процедуры.

Формат описания процедуры:

procedure имя (формальные параметры);

раздел описаний

begin

операторы

end;

Описание процедуры включает заголовок и тело процедуры. Заголовок состоит из зарезервированного слова procedure , идентификатора имя процедуры и списка формальных параметров с указанием типа параметра (список параметров может отсутствовать). Имя процедуры – идентификатор, уникальный в пределах программы. Тело процедуры представляет собой блок, по структуре аналогичный программе.

Рассмотрим пример процедуры, которая вычисляет aⁿ , где a и n – это данные целые числа (n0).

procedure degree( a,n:integer; var step:integer);

var i:integer;

begin

step1;

for i1 to n do stepstepa;

end;

Результатом выполнения процедуры может быть не одно значение, а несколько. Рассмотрим пример процедуры, меняющей местами значения двух переменных x и y.

procedure swap(var x, y:integer);

var z:integer;

begin

zx; xy; yz

end;


Функции.

Формат описания функции:

function имя (формальные параметры) : тип результата;

раздел описаний

begin

операторы

end;

Функция состоит из заголовка и тела функции. В отличие от процедуры результатом выполнения функции может быть только одно значение. В теле функции обязательно должен быть хотя бы один оператор присваивания, где в левой части стоит имя стандартной переменной result, а в правой – вычисленное значение функции.

Рассмотрим пример функции, которая вычисляет факториал числа n.

n! 123… n

function fact(n:integer):integer;

var i:integer; f:integer;

begin

f1; for i1 to n do ff  i;

resultf

end;


Вызов подпрограмм.

Описание процедур и функций в основной программе занимает место в конце раздела описаний, до начала блока операторов. При вызове процедуры или функции её формальные параметры заменяются фактическими. Число и тип формальных и фактических параметров должны совпадать. При этом фактические параметры должны располагаться в том же порядке, что и формальные.

Пример 26. Рассмотрим пример применения процедуры degree для решения следующей задачи: Вычислить y8x⁵  3x⁴  2x³.

var x:integer; y, z:integer;

procedure degree( a, n:integer; var step:integer);

var i:integer;

begin

step1;

for i1 to n do stepstepa;

end;

begin

readln(x);

degree(x, 5, z); y8z;

degree(x, 4, z); yy – 3z;

degree(x, 3, z); yy  2z;

writeln(y);

readln

end.

Вызов процедуры – это оператор, состоящий из имени процедуры, за которым в круглых скобках записаны фактические параметры, которые передают свои значения соответствующим формальным параметрам.

1^ый вызов xa 5n zstep

2^ой вызов xa 4n zstep

3^ий вызов xa 3n zstep

Вызов и выполнение функции производятся при вычислении значения указателя функции

<имя функции>(<список фактических параметров>),

который входит в некоторое выражение в вызывающей программе.

Пример 27. Описать функцию для вычисления n! (n13) и с её помощью вычислить



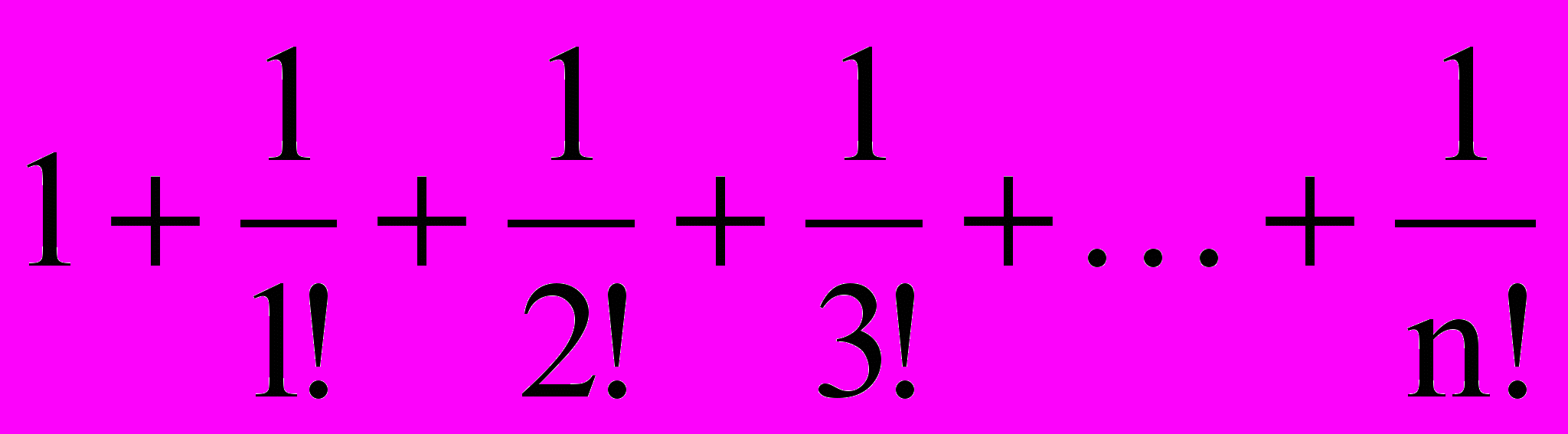
var n, k : integer; res : real;

function fact(n : integer) : integer;

var i, f : integer;

begin

f:=1;

for i:=1 to n do f:= f * i;

result:=f

end;

begin

readln(n);

res:=1;

for k:=1 to n do

res:=res + 1/fact(k);

writeln(res:8:3);

readln

end.