Дальтона законы

Вид материала

Закон

Содержание Рис. 5. а и б — отталкивающиеся и притягивающиеся дислокации; в и г — аннигиляция притягивающихся дислокаций. Движение дислокаций. Рис. 6. Перемещение дислокации в плоскости скольжения сопро­вождается разрывом и пересоединением межат. связей атомов у линии ди Рис. 7. Переползание краевой дислокации. Атомы лишней полуплоскости переходят в вакантные узлы решётки. Рис. 8. Электронно-микроскопич. снимок дислокац. структуры кристалла хрома после высокотемпературной деформации Дислокационная структура дефор­мированных кристаллов. Разрушение. Влияние дислокаций на физические свойства кристаллов. Рис 10. Ряды дислокаций в плоскостях скольжения в кристалле LiF, выявленные. методом травления. Косые ряды — краевые дислокации, Дисперсии закон U газа квазичастиц в кристалле объ­ёма V при темп-ре Т Де Хааза — ван Альфена эффект, Цик­лотронный резонанс, Размерные эф­фекты). Дисперсионные призмы Дисперсия волн Групповая скорость, Волновой пакет) Дисперсия диэлектрической проницаемости А. Л. Полякова.

Подобный материал:

• Вопросы к Госэкзамену по курсу общей физики из раздела, 17.7kb.
• Направление: Искусство и гуманитарные науки, 1316.91kb.
• Законы сохранения и принципы симметрии, 283.17kb.
• Программа профильного курса для 10-11-х классов средней общеобразовательной школы Ивлев, 503.96kb.
• Законы делимости (дискретности) в мире животных и растений. Законы наследственности, 276.87kb.
• Законы Кеплера законы движения планет, 184.9kb.
• Авторское право. Терминология, 213.44kb.
• Законы ману, 3773.29kb.
• Исследование о влиянии эволюционной теории на учение о политическом развитии народов, 10156.41kb.
• Исследование о влиянии эволюционной теории на учение о политическом развитии народов, 6089.9kb.

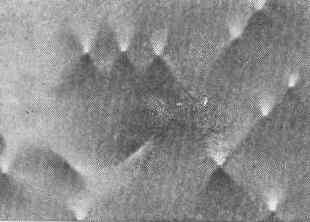
Рис. 4. Поля упругих напряжений вокруг краевых дислокаций в кристалле кремния, выявленные методом фотоупругости. Дисло­кации пронизывают пластинку кремния пер­пендикулярно к плоскости рисунка.


Между предельными случаями кра­евой и винтовой Д. возможны любые промежуточные. В общем случае линия Д. может представлять собой произвольную пространств. кривую, вдоль к-рой вектор Бюргерса остаётся постоянным (и равным к.-л. вектору трансляции решётки), хотя ориен­тация Д. может изменяться.


Линии Д. не могут обрываться внутри кри­сталла, они должны либо быть замкнутыми, образуя петли, либо разветв­ляться на неск. Д., либо выходить на поверхность кристалла.



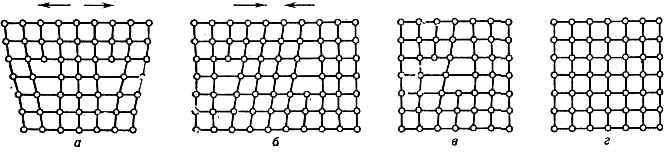
Рис. 5. а и б — отталкивающиеся и притягивающиеся дислокации; в и г — аннигиляция притягивающихся дислокаций.


Плотность Д. в кристалле определяется как ср. число линий Д., пересекающих внутри тела площадку в 1 м², или как сум­марная длина Д. в 1 м³. Плотность Д. обычно колеб­лется от 10⁶ до 10⁷ на 1 м² в наиб. совершенных мо­нокристаллах и до 10¹⁵—10¹⁶ на 1 м² в

сильно искажен­ных (наклёпанных) металлах (см. ниже).

Участки кристалла вблизи Д. нахо­дятся в упругонапряжённом состоя­нии. Напряжения убывают обратно пропорц. расстоянию от Д. Поля напряжений вблизи отдельных Д. выявляются (в прозрачных кристаллах с низкой плотностью Д.) с помощью поляризов. света (рис. 4). Величина упругой энергии, обусловленной полем напряжений Д., пропорц. b² и со­ставляет обычно ~10^-13 Дж на 1 м длины Д. При сближении двух Д. с одинаковыми векторами b (рис. 5, а) упругие напряжения около Д. уве­личиваются и Д. отталкиваются. При сближении Д. с противоположными векторами Бюргерса их упругие поля взаимно компенсируются (рис. 5, б, в, г); Д. притягиваются и аннигилируют.

Движение дислокаций. Поскольку Д. обладает собств. полем напряжений, она под действием внешних приложен­ных к кристаллу напряжений испыты­вает силу, под действием к-рой прихо­дит в движение, результатом чего явля­ется взаимное «проскальзывание» ат. плоскостей —пластич. деформация.

При перемещении Д. в плоскости скольжения в каждый данный мо­мент разрываются и пересоединяют­ся связи не между всеми атомами на плоскости скольжения, а толь­ко между теми атомами, к-рые нахо­дятся у линии Д. (рис. 6). Поэтому пластическая деформация сдвига мо­жет происходить при сравнительно малых внеш. напряжениях. Эти на­пряжения на неск. порядков ниже, чем напряжение, при к-ром может пластически деформироваться совер­шенный кристалл без Д. путём раз­рыва всех межат. связей в плоскости скольжения (теор. прочность на сдвиг, см. Пластичность).

Движение краевых Д. по нормали к плоскости скольжения (п е р е п о л з а н и е) осуществляется путём при­соединения или отрыва вакансий от края плоскости (рис. 7). Оно связано с диффузионным переносом массы, пластич. деформацией и происходит при высоких темп-рах.



Рис. 6. Перемещение дислокации в плоскости скольжения сопро­вождается разрывом и пересоединением межат. связей атомов у линии дислокации.


Подвижность дислокаций. Движе­нию Д. препятствует не только проч­ность разрываемых межат. связей, но и рассеяние фононов и электронов проводимости в упруго искажённой области кристалла, окружающей движущиеся Д. Движению Д. мешают также упругое вз-ствие с др. Д. и с примесными атома­ми, межзёренные границы в поли­кристаллах, ч-цы др. фазы в рас­падающихся сплавах, двойники (см. Двойникование) и др. дефекты в кри­сталлах. На преодоление этих пре­пятствий тратится часть работы внеш. сил. Т. о., кристалл с Д. «мягче» бездефектного кристалла, но если он «набит» Д. и др. дефектами настоль­ко, что они мешают друг другу, то

164




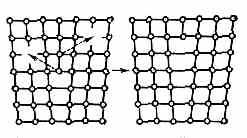
Рис. 7. Переползание краевой дислокации. Атомы лишней полуплоскости переходят в вакантные узлы решётки.


кристалл снова становится «жё­стким».

Образование и исчезновение дисло­каций. Обычно Д. возникают при образовании кристалла из расплава или из газообразной фазы (см. Кри­сталлизация). Методы выращивания бездислокац. монокристаллов очень сложны и разработаны только для немногих в-в. После тщательного от­жига кристаллы содержат обычно 10⁸—10⁹ Д. на 1 м². Притягиваю­щиеся Д. с противоположными век­торами Бюргерса, лежащие в одной плоскости скольжения, при сближении уничтожают друг друга (аннигили­руют, рис. 5, б, в, г). Если такие Д. лежат в разных плоскостях скольже­ния, то для их аннигиляции требуется переползание. Поэтому при высоко­температурном отжиге, способствую­щем переползанию, плотность Д. по­нижается. Искривление ат. плоско­стей вблизи Д. изменяет сечение рас­сеяния рентг. лучей и эл-нов. На этом основаны рентг. и электронно-микроскопич. методы наблюдения Д. (рис. 8).

Основными механизмами размноже­ния Д. в ходе пластич. деформации являются т. н. источники Фран­ка — Рида и двойное поперечное скольжение. Источником Франка — Рида может служить отрезок Д., за­крепленный на концах. Под прило­женным напряжением он прогибается,



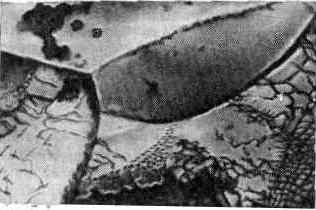
Рис. 8. Электронно-микроскопич. снимок дислокац. структуры кристалла хрома после высокотемпературной деформации


пока не отщепится замкнутая петля Д. и восстановится исходный отрезок. При двойном поперечном скольжении точками закрепления служат концы отрезков винтовой Д., вышедшей в др. плоскость скольжения и повер­нувшей затем в плоскость, параллель­ную первичной.

Дислокационная структура дефор­мированных кристаллов. Разрушение. С ростом пластич. деформации число

Д. растёт, ср. расстояния между ними сокращаются, их поля упругих на­пряжений взаимно перекрываются и скольжение Д. затрудняется (деформац. упрочнение). Чтобы скольжение Д. могло продолжаться, приложенное внеш. напряжение необходимо повы­сить. При дальнейшем размножении Д. внутр. напряжения могут дости­гать значений, близких к теор. проч­ности. При превышении предела проч­ности наступает разрушение кристал­ла — зарождаются и растут микро­трещины (рис. 9).



Рис. 9. Ат. плоскости, окаймляющие трещи­ну в кристалле фталоцианида меди: а — электронно-микроскопич. фото/рафия (меж­плоскостное расстояние 12,6 А); б — схема расположения ат. плоскостей.

Влияние дислокаций на физические свойства кристаллов. Д. влияют не только на такие механич. св-ва, как пластичность и прочность, для к-рых присутствие Д. явл. определяющим, но и на др. физ. св-ва кристаллов. Напр., с увеличением плотности Д. возрастает внутреннее трение, изменяются оптич. св-ва, повышается электросопротив­ление металлов. Д. увеличивают ср. скорость диффузии в кристалле, ус­коряют старение и др. процессы, связанные с диффузией, уменьшают

хим. стойкость кристалла, так что в результате обработки поверхности кри­сталла спец. в-вами (травителями) в местах выхода Д. образуются видимые ямки. На этом основано выявление Д. в непрозрачных материалах методом избирательного травления (рис. 10).



Рис 10. Ряды дислокаций в плоскостях скольжения в кристалле LiF, выявленные. методом травления. Косые ряды — краевые дислокации, вертикальный ряд — винтовые.


• Б ю р е н X. Г. в а н, Дефекты в кристал­лах, пер. с англ., М., 1962; Ф р и д е л ь Ж., Дислокации, пер. с англ., М., 1967; И н д е н б о м В. Л., Орлов А. Н., Физическая теория пластичности и прочности, «УФН»,

1962, т. 76, в. 3, с. 557; К о т т р е л л А. X., Теория дислокаций, пер. с англ., М., 1969; X и р т Дж., Лоте И., Теория дислока­ций, пер. с англ., М., 1972. А. Н. Орлов.

ДИСПЕРСИИ ЗАКОН, 1) зависимость частоты со волны от её волнового век­тора k (см. Дисперсия волн).

2) В квант. теории твёрдого тела Д. з.— зависимость энергии ξ ква­зичастицы от её квазиимпульса р: ξ=ξ(р). Периодич. строение кри­сталлов приводит к тому, что ξ(р) — периодич. ф-ция: ξ(p+2hb)=ξ(p), где b — произвольный вектор обрат­ной решётки. Д. з. позволяет опре­делить скорость квазичастицы v= dξ/dp, её эффективную массу и дви­жение во внеш. силовых полях (сла­бых по сравнению с внутриатомными).

Знание Д. з. достаточно для вычис­ления термодинамич. хар-к тв. тела как «газа» квазичастиц. Так, энергия U газа квазичастиц в кристалле объ­ёма V при темп-ре Т равна:



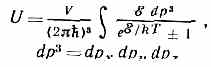
(интегрирование ведётся в пределах одной ячейки обратной решётки). Для вычисления термодинамич. хар-к удоб­но пользоваться плотностью энергетич. состояний v(ξ), т. е. числом состояний на ед. интервал энергии (ξ, ξ+dξ). Вблизи осн. состояния, где энергетич. состояние кристалла определяется квазичастицами:



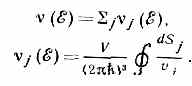
Здесь j — тип квазичастицы; dS_j — элемент площади на изоэнергетич. поверхности ξ_j(p)=ξ, по к-рой ведёт­ся интегрирование; v_j=│дξ_j/dp│.

Д. з. необходим для понимания кинетич. явлений в конденсиров. сре­дах. Эффективность вз-ствия квази­частиц в большой мере зависит от их Д. з. В частности, нек-рые про­цессы столкновений (или взаимопре­вращений) квазичастиц запрещены, т. к. при этом для определённых Д. з. не выполняются законы сохранения квазиимпульса и энергии.

Д. з. квазичастиц вычисляют, ис­ходя из симметрии кристалла или структуры среды и из предположений о силах, действующих между её ато­мами. Д. з. квазичастиц — бозонов определяют гл. обр. методом неуп­ругого рассеяния нейтронов (см. Ней­тронография) и фотонов (см., напр., Мандельштама — Вриллюэна рас­сеяние), а также по резонансным эф­фектам. Все эти методы объединяет общая идея: рождение или гибель бозона сопровождается изменением энергии и импульса др. ч-цы с из­вестным Д. з. Законы сохранения квазиимпульса и энергии квазича­стицы позволяют определить её Д. з.

165


Для фермионов Д. з. определяют, как правило, по поведению проводников в сильном пост. магн. поле (см. Де Хааза — ван Альфена эффект, Цик­лотронный резонанс, Размерные эф­фекты). Общая идея этих методов — выделение небольшой группы квази­частиц — фермионов, ответственных за эффект. При движении в магн. поле энергия заряж. ч-цы не изменяется, т. е. ч-ца движется по изоэнергетич. поверхности, форма и размеры к-рой проявляются в наблюдаемых эффек­тах, если между столкновениями ч-ца успеет неск. раз описать траекторию. Этому благоприятствует увеличение магн. поля.

3) В теории квант. жидкостей Д. з.— зависимость энергии элем. возбуж­дения жидкости от импульса (см. Сверхтекучесть, Ферми-жидкость).

• См. лит. при ст. Квазичастица.

М. И. Каганов.

ДИСПЕРСИОННЫЕ ПРИЗМЫ, то же, что спектральные призмы.

ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ,

соотношения между величинами, опи­сывающими реакцию физ. системы на внеш. воздействие. Д. с. не зависят от конкретного механизма вз-ствия системы с внеш. воздействием и явл. прямым следствием принципа при­чинности, заключающегося в данном случае в том, что реакция системы по времени не может опережать внеш. воздействие.

Д. с. впервые были получены в теории дисперсии света как связь между показателями преломления и поглощения света в среде (или между действит. и мнимой частями диэлектрич. проницаемости — Крамерса — Кронига соотношения). В квант. ме­ханике и квант. теории поля (КТП) Д. с. выступают как связь между вещественной (Re) и мнимой (Im) частями амплитуд процессов. (Стро­гое доказательство Д. с. в КТП было впервые дано Н. Н. Боголюбовым в 1956.) Напр., для амплитуды рас­сеяния f двух ч-ц как ф-ции энергии ξ, f(ξ), Д. с. записываются в виде:



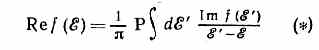
(Р — символ гл. значения интеграла), причём интегрирование ведётся по области энергии, где Imf0. В нек-рых случаях Д. с. допускают непосредств. проверку, к-рая в сущности означает проверку принципа причинности. Напр., для рассеяния на нулевой угол (рассеяние вперёд) мнимая часть амплитуды благодаря оптической тео­реме пропорц. полному сечению про­цесса, измеряемому экспериментально. Несколько более сложная процедура позволяет измерить также и веществ. часть амплитуды. Подставляя ре­зультаты этих измерений в Д. с. типа (*), можно судить, в какой степени выполняется это равенство.

Проведённая проверка показала, что вплоть до энергий, соответствующих расстояниям 5•10^-16 см, равенство (* ), а следовательно, и принцип при­чинности выполняются.

Другая область применения Д. с. в теории элем. ч-ц связана с исполь­зованием унитарности условия и пе­рекрёстной симметрии, к-рые позво­ляют выразить мнимую часть ампли­туды одного процесса через ампли­туды других процессов. Напр., в определ. области энергий мнимая часть формфактора протона связывается с амплитудой аннигиляции р+р ⁺+^-. Т. о. удаётся установить взаимосвязь между разл. физ. про­цессами. Возникающая система ур-ний оказывается настолько широкой, что практически включает все возмож­ные процессы, происходящие с элем. ч-цами, и не поддаётся матем. разре­шению. В ряде случаев, однако, с помощью разл. приближений удаётся сузить систему взаимосвязей про­цессов и получить важные физ. результаты. В частности, на основе такого дисперс. анализа формфак­тора протона было получено пред­сказание существования -мезона, к-рый вскоре был обнаружен экспе­риментально.

Несмотря на то что программа полного построения амплитуд про­цессов в рамках дисперс. подхода не нашла окончат. решения, Д. с. прочно вошли в аппарат теории элем. ч-ц и КТП и служат мощным инструмен­том исследования св-в амплитуд про­цессов.

• Боголюбов Н. Н., Медведев Б. В., Поливанов М. К., Вопросы теории дисперсионных соотношений, М., 1958; Хагедорн Р., Причинность и дис­персионные соотношения, пер. с англ., «УФН», 1967, т. 91, в. 1, с. 151.

А. В. Ефремов.

ДИСПЕРСИЯ ВОЛН (от лат. dispersio — рассеяние), зависимость фазо­вой скорости v_ф гармонич. волны от её частоты . Простейшим примером явл. Д. в. в линейных однородных средах, характеризуемая т. н. дисперс. урав­нением (законом дисперсии); оно связывает частоту и волн. число k плоской гармонич. волны: =(k) (а в анизотропных средах — частоту и волн. вектор k). Дисперс. уравне­ние может иметь неск. ветвей, к-рым соответствуют разл. типы волн (моды). Напр., в изотропной плазме — это ветви, относящиеся к эл.-магн., плаз­менным и ионно-звук. волнам.

Если фазовая скорость волн в нек-ром частотном интервале постоян­на, говорят, что в этом интервале Д.в. отсутствует. Примером волн без дис­персии явл. эл.-магн. волны в ва­кууме. В большинстве случаев Д. в. обусловлена микромасштабными св-вами среды (колебаниями атомов и мо­лекул, их тепловым движением, крист. структурой и т. д.), такие среды наз. диспергирующими. Различают вре­менную (частотную) и пространствен­ную дисперсию. Временная — определяется запаздыванием (инерцией) от­клика к.-л. физ. величины (напр., электрич. поляризации или механич. смещения) на приложенное внеш. воз­действие (электрич. поле или давле­ние). Пространственная Д. в. возни­кает, когда поведение элемента среды зависит от воздействия не только на него, но и на соседние элементы, т. е. имеет место нелокальность от­клика среды на внеш. воздействие. Во мн. случаях, однако, вклад дис­персий обоих типов в закон дисперсии =kv_ф(, k) формально неразличим. Д. в. наз. нормальной или отрицательной, если показа­тель преломления n=const/v_ф растёт

с частотой (дn/д>0, дv_ф/д<0), и аномальной или положи­тельной при выполнении обрат­ных неравенств. Из причинности прин­ципа следует, что в отсутствии потерь энергии (в недиссипативных средах) чисто временная Д. в. всегда нор­мальная, аномальность появляется лишь в полосах поглощения. Однако в средах с пространств. дисперсией это правило может нарушаться.

Понятие Д. в. применимо к любым нормальным волнам в направляющих системах, напр. в волноводах. При этом Д. в. обусловлена конфигурацией вол­новодов, неоднородностями сред, мет­рикой пр-ва и т. д. В простейших слу­чаях удаётся обобщить понятия Д. в. и на нелинейные волны, когда можно разделить параметры, ответственные за нелинейность и дисперсию в среде.

В линейных средах Д. в. всегда приводит к размыванию волн. воз­мущения (см. Групповая скорость, Волновой пакет); при наличии не­линейности возможно конкурирующее сжатие волн. пакета. В результате могут возникать стационарные не­линейные волны, как периодические, так и уединённые (напр., солитоны).

Д. в. обусловливает мн. природные явления и широко используется в технике. Напр., все разновидности радуг объясняются спектр. расщеп­лением (из-за дисперсии света) и дифракцией солн. лучей в дож­девых каплях. Д. в. в ионосферной плазме определяет частоту радиосиг­налов, отражающихся в данном слое ионосферы (см. Распространение ра­диоволн). На Д. в. основаны принципы действия мн. радиотехн., оптич. и др. устройств: рефрактометров, ан­тенн с частотным сканированием диа­грамм направленности и т. д. См. также Дисперсия звука.

• Уизем Дж., Линейные и нелинейные волны, пер. с англ., М., 1977; Б о р н М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973.

А. Я. Басович, М. А. Миллер.

ДИСПЕРСИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ, см. в ст. Ди­электрическая проницаемость.

ДИСПЕРСИЯ ЗВУКА (дисперсия скорости звука), зависимость фазовой скорости гармонич. звук. волн от их частоты. Д. з. может быть обусловлена

166


как физ. св-вами среды, так и при­сутствием в ней посторонних вклю­чений и наличием границ тела, в к-ром авук. волна распространяется. Д. з., связанная с физ. св-вами среды, возникает, когда воздействие акустич. волны приводит к неравно­весному состоянию среды, возбуждая её внутр. степени свободы (колебат. и вращат. движения молекул), про­цессы ионизации и диссоциации мо­лекул, хим. реакции, перестройку структуры жидкости, процессы взаи­модействия ультразвука с электро­нами проводимости в металлах и ПП, магнитоупругие явления и т. д. Вы­равнивание энергии между поступат. и внутр. степенями свободы происхо­дит за нек-рое время, наз. временем релаксации _р (см. Релаксация аку­стическая). Если период Т звук. волны мал по сравнению с _р (вы­сокие частоты), то за время Т<<_p внутр. степени свободы не успевают возбудиться, поэтому среда будет ве­сти себя так, как будто внутр. сте­пени свободы отсутствуют. Если же 7>>_р (низкие частоты), то часть энергии поступат. движения успеет перераспределиться на внутр. степени свободы. При этом, вследствие умень­шения энергии по­ступат. движения, упругость среды и скорость звука так­же будут меньше, чем в случае вы­соких частот. Т. о., при наличии релаксации скорость звука увеличи­вается с ростом частоты (рис.).



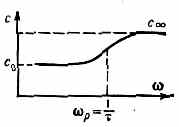
Бы­стрее всего рост скорости происходит при частотах, близких к частоте ре­лаксации _р=1/ (дисперс. область). Для большинства сред _р лежит в области УЗ и гиперзвуковых частот. Если с₀ — скорость звука при малых частотах (<<1), а c_ — при очень больших (>>1), то скорость звука для произвольной частоты со описы­вается ф-лой:



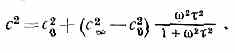
Такая зависимость с () характерна для всех релаксац. процессов в од­нородных средах. Д. з. сопровожда­ется также повышенным поглощением звука сравнительно с поглощением, обусловленным сдвиговой вязкостью и теплопроводностью.

Д. з. в газах связана с возбуж­дением колебат. и вращат. степеней свободы молекул, а в жидкостях — с колебательной и поворотно-изомер­ной релаксациями и перестройкой внутр. структуры жидкости, а также с процессами диссоциации, хим. ре­акциями и т. д. В тв. телах Д. з. обычно появляется, когда акустич. волна взаимодействует с к.-л. видами внутр. возбуждений, и под её воздей­ствием происходит изменение состоя­ния эл-нов проводимости, системы спинов, спиновых волн и др.

Величина Д. з., определяемая как =(с_-c₀)/c₀, может сильно разли­чаться для разных в-в. Так, напр., в углекислом газе 4%, в бензоле 10%, в морской воде <0,01, а в очень вязких жидкостях и в вы­сокополимерных соединениях скорость звука может изменяться на десятки процентов. Частотный диапазон, в к-ром имеет место Д. з., также раз­личен для разных в-в. Так, в угле­кислом газе при нормальном дав­лении и темп-ре 18°С _р=28 кГц, в морской воде _р=120 кГц. В четырёххлористом углероде, бензоле, хло­роформе и др. область релаксации попадает в область частот ~10⁹— —10¹⁰ Гц.

К Д. з. того же типа, но не носящей релаксац. хар-ра, приводят тепло­проводность и вязкость среды. Эти виды Д. з. обусловлены обменом энер­гией между областями сжатий и раз­режений в звук. волне и особенно существенны для микронеоднородных сред. Д. з. может проявляться также в среде с вкрапленными неоднородностями (резонаторами), напр. в воде, содержащей пузырьки газа. В этом случае при частоте звука, близкой к резонансной частоте пузырьков, часть энергии звук. волны идёт на возбуж­дение колебаний пузырьков, что при­водит к Д. з. и к возрастанию по­глощения звука.

Как правило, Д. з. лгала, за исклю­чением нек-рых спец. случаев, таких, как неоднородная среда (напр., пу­зырьки газа в воде) или очень вы­сокие частоты.

Принципиально другим типом Д. з. явл. «геометрическая» дисперсия, обус­ловленная наличием границ тела или среды. Она появляется при распро­странении волн в стержнях, пласти­нах, в любых волноводах акустических. Для изгибных волн Д. з. наблюда­ется в тонких пластинах и стержнях (их толщина должна быть много мень­ше, чем длина волны). При изгибании тонкого стержня упругость на изгиб тем больше, чем меньше изгибаемый участок. При распространении изгибной волны длина изгибаемого уча­стка определяется длиной волны зву­ка. Поэтому с уменьшением длины волны (с повышением частоты) уве­личивается упругость, а следователь­но, и скорость распространения волны. Фазовая скорость такой волны пропорц. .

При распространении звука в вол­новодах звук. поле можно представить как суперпозицию нормальных волн, фазовые скорости к-рых для прямо­угольного волновода с жёсткими стен­ками определяются соотношением:



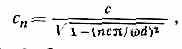
где n=1, 2, 3, . . .— номер нормаль­ной волны, с — скорость звука в свободном пр-ве, d — поперечный раз­мер волновода. Фазовая скорость нор­мальной волны всегда больше скорости звука в свободной среде и уменьшается с ростом частоты.

Д. з. обоих типов приводит к расплыванию формы звук. импульса при его распространении. Это особенно важно для гидроакустики, атмосфер­ной акустики и геоакустики, где имеют дело с распространением звука на большие расстояния, а также для УЗ линий задержки.

• Михайлов И. Г., Соловьев А., Сырников Ю. П., Основы мо­лекулярной акустики, М., 1964; Физическая акустика, под ред. У. Мэзона, пер. с англ., т. 2, ч. А, М., 1968, т. 5, М., 1973, гл. 4; Труэлл Р., Эльбаум Ч., Ч и к Б., Ультразвуковые методы в физике твердого тела, пер. с англ., М., 1972.

А. Л. Полякова.