1. Статистический анализ показателей, характеризующих деятельность цирков Российской Федерации
| Вид материала | Реферат |
СодержаниеКоличество зрителей * 100% = % посещения. (3.1) Количество мест * количество представлений |
- Тема курсовой работы, 22.7kb.
- Тенденции формирования социальной структуры российского общества на современном этапе, 447.36kb.
- Агентство Республики Казахстан по статистике Департамент статистики труда и уровня, 317.93kb.
- Методика аудиторской проверки учета кассовых операций студентки 5 курса Факультет:, 530.73kb.
- Стратегия государственной молодежной политики в российской федерации (Министерство, 484.32kb.
- Бакалаврская программа № 521200 Кафедра: Социологии Направление : Социология Дисциплина, 188.47kb.
- Институт, 132.47kb.
- Статистический отчет ежегодный документ Ежегодный статистический отчет составляется, 2030.09kb.
- Всистеме показателей, характеризующих эффективность производства и реализации, одно, 317.59kb.
- Всистеме показателей, характеризующих эффективность производства и реализации, одно, 49.75kb.
Количество зрителей * 100% = % посещения. (3.1)
Количество мест * количество представлений
Данная формула применяется для расчета посещаемости в бухгалтерском учете Росгосцирка.
Следовательно, фактор количество зрителей и количество представлений нецелесообразно включать в регрессионную модель, так как возникает опасность мультиколлинеарности и, как следствие, статистической не надежности модели. Фактор количество мест решено включить в модель из экономических соображений. Построение уравнения регрессии предполагает решение двух основных задач.
Первая задача заключается в выборе независимых переменных, в нашем примере расход, количество мест, посещение, оказывающих существенное влияние на зависимую переменную (доход), а также в определении вида уравнения регрессии.
Вторая задача построения уравнения регрессии – оценивание параметров уравнения. Она решается с помощью того или иного математико-статистического метода обработки данных.
Для анализа статистически данных был применен пакет прикладных программ Статистика 5,0 - ППП “Statistica”. Переменные, которые будут использоваться в многомерном статистическом анализе, имеют различные единицы измерения. Поэтому перед проведением статистического анализа данные стандартизировались, то есть приводились к единой шкале измерений.
В пакете прикладных программ Статистика 5,0, команда Standardize Rows Columns (стандартизация строк), позволяет выполнить стандартизацию значений в каждой строке выделенного блока. Значения переменных в блоке изменяются на стандартизированные, которые вычисляются по следующей формуле (3.2):
новое значение = (старое значение – среднее в выделенной строке)/стандартное отклонение,
t = x – x . (3.2)
s
Далее, с целью получения однородных статистических совокупностей, был проведен кластерный анализ.
Кластерный анализ - это общее название множества вычислительных процедур, используемых при создании классификации. Это многомерная статистическая процедура, выполняющая сбор данных, содержащая информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы.
В качестве расстояния между объектами принимались различные расстояния, обычное евклидово расстояние, взвешенное евклидового расстояния. При объединении в группы в кластерном анализе были рассмотрены дендограммы (приложение № 4.) сделанные, двумя иерархическими методами: методом дальнего соседа (Complete Linkage) и методом Уорда (Ward's method).
Графическое представление результатов кластерного анализа будет осуществляться с помощью ППП “Statistica”. Кластерный анализ проводится в одном, выше рассмотренном, статистическом пакете прикладных программ. Все дендограммы представлены в приложении № 4.
Таким образом, используя несколько алгоритмов кластерного анализа, отдадим предпочтение разбиению на два кластера методом Уорда. В методе «Уорда» в данной дипломной работе будет применяться взвешенное евклидовое расстояние.
На рис. 3.1 представлена дендограмма классификации городов на основе взвешенного евклидового расстояния и принципа Уорда.
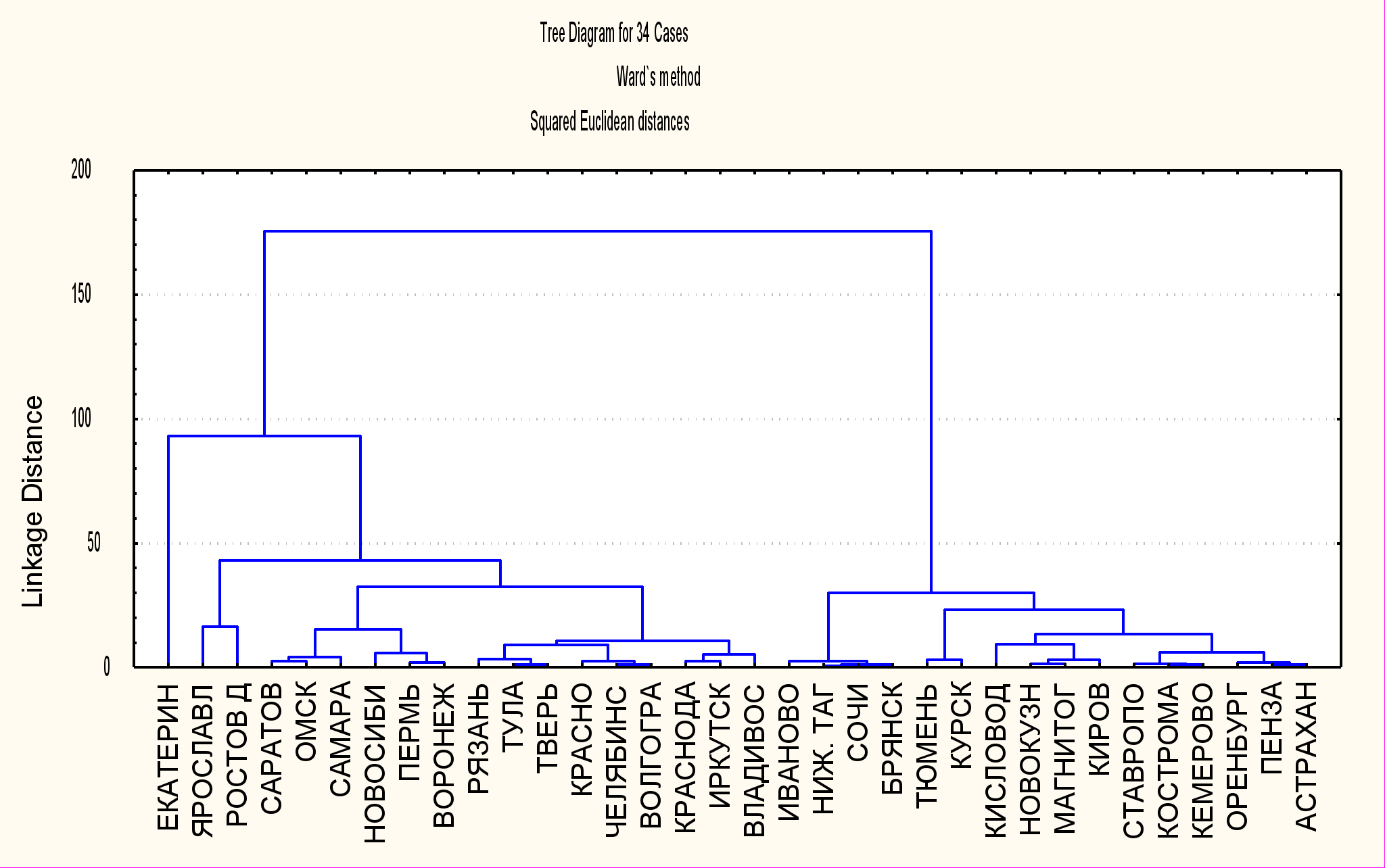
Рис. 3.1. Дендограмма. Классификация городов на основе взвешенного евклидового расстояния и принципа Уорда.
Классификация проводилась по различным алгоритмам кластерного анализа, но наилучшими в содержательном плане оказались результаты, полученные методом Уорда при разбиении на два кластера, первый: состоящий из 18 городов, и второй: из 16 городов.
Таким образом, были получены две статистически однородные группы. В нашем примере, следует остановиться на применении именно этого метода, как наилучшего варианта классификации. Результаты кластерного анализа представлены в таблице № 3.1.
Таблица № 3.1. Города, вошедшие в первый и второй кластеры.
| № п/п | 1 кластер | № п/п | 2 кластер |
| 1 | Владивосток | 1 | Астрахань |
| 2 | Волгоград | 2 | Брянск |
| 3 | Воронеж | 3 | Иваново |
| 4 | Иркутск | 4 | Кемерово |
| 5 | Краснодар | 5 | Киров |
| 6 | Красноярск | 6 | Кисловодск |
| 7 | Тверь | 7 | Кострома |
| 8 | Екатеринбург | 8 | Курск |
| 9 | Самара | 9 | Сочи |
| 10 | Новосибирск | 10 | Магнитогорск |
| 11 | Омск | 11 | Нижний Тагил |
| 12 | Пермь | 12 | Новокузнецк |
| 13 | Ростов Дон | 13 | Оренбург |
| 14 | Рязань | 14 | Пенза |
| 15 | Саратов | 15 | Ставрополь |
| 16 | Тула | 16 | Тюмень |
| 17 | Челябинск | | |
| 18 | Ярославль | | |
