1. Статистический анализ показателей, характеризующих деятельность цирков Российской Федерации

Вид материала

Реферат

Содержание 2. Методологический аспект анализа деятельности цирков Российской Федерации. количество зрителей 2.2. Алгоритм анализа деятельности цирков РФ с помощью методов математической статистики.

Подобный материал:

• Тема курсовой работы, 22.7kb.
• Тенденции формирования социальной структуры российского общества на современном этапе, 447.36kb.
• Агентство Республики Казахстан по статистике Департамент статистики труда и уровня, 317.93kb.
• Методика аудиторской проверки учета кассовых операций студентки 5 курса Факультет:, 530.73kb.
• Стратегия государственной молодежной политики в российской федерации (Министерство, 484.32kb.
• Бакалаврская программа № 521200 Кафедра: Социологии Направление : Социология Дисциплина, 188.47kb.
• Институт, 132.47kb.
• Статистический отчет ежегодный документ Ежегодный статистический отчет составляется, 2030.09kb.
• Всистеме показателей, характеризующих эффективность производства и реализации, одно, 317.59kb.
• Всистеме показателей, характеризующих эффективность производства и реализации, одно, 49.75kb.

2. Методологический аспект анализа деятельности цирков Российской Федерации.

2.1 Обоснование возможностей применения методов математической статистики для анализа деятельности цирков Российской Федерации.


Методы математической статистики широко применяются в различных областях экономики и предназначены для обоснованного принятия экономических решений. Применение методов математической статистики в деятельности цирковых предприятий на современном этапе, в условиях рыночной экономики, становится более чем актуальным. Ранее, экономико-статистический анализ не проводился, и данная дипломная работа является первой, применив методы математической статистики для анализа деятельности цирков Российской Федерации.

Деятельность цирков Российской Федерации характеризуется целым рядом факторов определяющих эффективность их деятельности. Зависимость успеха работы цирка определяются в основном следующими факторами:

• население;
  
• количество мест в цирке;
  
• количество представлений;
  

• количество зрителей;

• доходы;
  
• расходы;
  
• прибыль;
  
• посещаемость.
  

Однако некоторые факторы являются в некотором роде частью других факторов. Для выбора факторов, характеризующих деятельность цирков Российской Федерации, целесообразно использовать методы математической статистики:

• корреляционный анализ;
  
• многомерный регрессионный анализ.
  

Методы математической статистики позволяют отобрать факторы, оказывающие наибольшее влияние на успех хозяйственной деятельности цирков. Для получения статистической надежности модели целесообразно использовать методы кластерного анализа, с помощью которого статистический материал становится однородным.

Предварительный анализ литературы, касающийся деятельности цирков Российской Федерации показал что, для анализа деятельности цирков Российской Федерации, методы математической статистики не применялись.

Эффективность применения методов математической статистики для анализа деятельности в различных сферах экономики доказана, и по нашему мнению применение их, для анализа деятельности цирков Российской Федерации является обоснованным.

Статистический материал, предоставленный Государственным комитетом статистики и Российской государственной цирковой компанией, свидетельствует о том, что применение методов математической статистики позволяет ответить на ряд вопросов, касающихся непосредственных причин упадка в области циркового искусства.

2.2. Алгоритм анализа деятельности цирков РФ с помощью методов математической статистики.

Прежде чем проводить многомерный статистический анализ необходимо определить природу изучаемых переменных. Переменные (признаки) могут быть: количественные, то есть скалярно измеряющие, в определенной шкале, степень проявления изучаемого свойства объекта (объем продукции, численность работников предприятия, суммы денежного дохода и т.п.); порядковые (или ординальные), позволяющие упорядочить анализируемые объекты по степени проявления в них изучаемого свойства (уровень образования работника, квалификационный разряд рабочего и т.п.); классификационные (или номинальные), позволяющие разбивать обследованную совокупность объектов на не поддающиеся упорядочиванию однородные (по анализируемому свойству) классы (профессия работника, мотив миграции семьи, отрасль промышленности и т.п.).

Природа результирующих показателей (эндогенных переменных) может совпадать с природой объясняющих (экзогенных) переменных, а может быть и различной. В зависимости от этого возможно применение тех или иных методов многомерного статистического для анализа деятельности цирков РФ. Существует и смешанная природа тех или иных показателей, которая включает в себя количественные и неколичественные переменные.

Переменные, которые будут использованы для построения многомерной регрессионной модели, имеют различные единицы измерения. Поэтому перед проведением статистического анализа данные будут стандартизироваться, то есть приводится к единой шкале измерений. Для проведения статистического анализа в дипломной работе будет проведен кластерный анализ.

В статистических исследованиях группировка первичных данных является основным приемом решения задачи классификации, а поэтому и основой всей дальнейшей работы с собранной информацией.

При наличии нескольких признаков задача классификации может быть решена методами кластерного анализа, которые отличаются от других методов многомерной классификации отсутствием обучающих выборок. Основой статистических постановок задачи кластерного анализа является вероятностная модель исследуемого процесса. Статистический подход удобен для теоретического исследования проблемы, связанного с кластерным анализом. Кроме того, оно дает возможность ставить задачи, связанные с воспроизводимостью результатов кластерного анализа.

Кластерный анализ - это общее название множества вычислительных процедур, используемых при создании классификации. Это многомерная статистическая процедура, выполняющая сбор данных, содержащая информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы. Кластерный анализ позволяет группировать данные вокруг нескольких центров в n- мерном пространстве.

Этот анализ – одно из направлений статистического исследования. Особо важное место он занимает в тех отраслях науки, которые связаны с изучением массовых явлений и процессов. Необходимость развития методов кластерного анализа и их использования продиктована, прежде всего, тем, что они помогают построить научно обоснованные классификации, выявить внутренние связи между единицами наблюдаемой совокупности. Кроме того, методы кластерного анализа могут использоваться с целью сжатия информации, что является важным фактором в условиях постоянного увеличения и усложнения потоков статистических данных.

Цель кластерного анализа заключается в поиске существующих структур, в то же время его действие состоит в привнесении структуры в анализируемые данные, т.е. методы кластеризации необходимы для обнаружения структуры в данных, которую нелегко найти при визуальном обследовании или с помощью экспертов.

Для проведения кластерного анализа будет использован следующий алгоритм разбиения совокупности n объектов на однородные в некотором смысле группы (классы). Полученные в результате разбиения группы обычно называются кластерами. Кластеры могут быть относительно близки друг к другу и не иметь четких границ, или же они могут быть разделены широкими участками пустого пространства.

В кластерном анализе используются различные меры расстояния между объектами.

• евклидово расстояние: 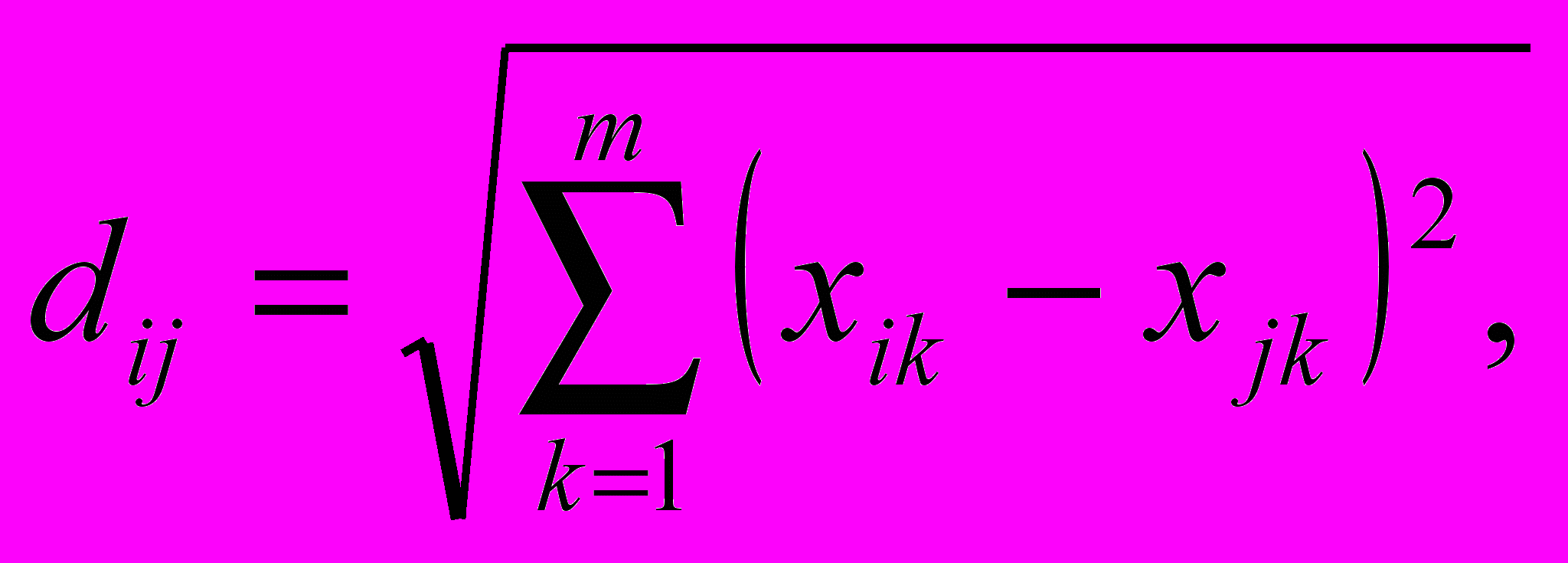(2.1)
  
• взвешенное евклидово расстояние:
  

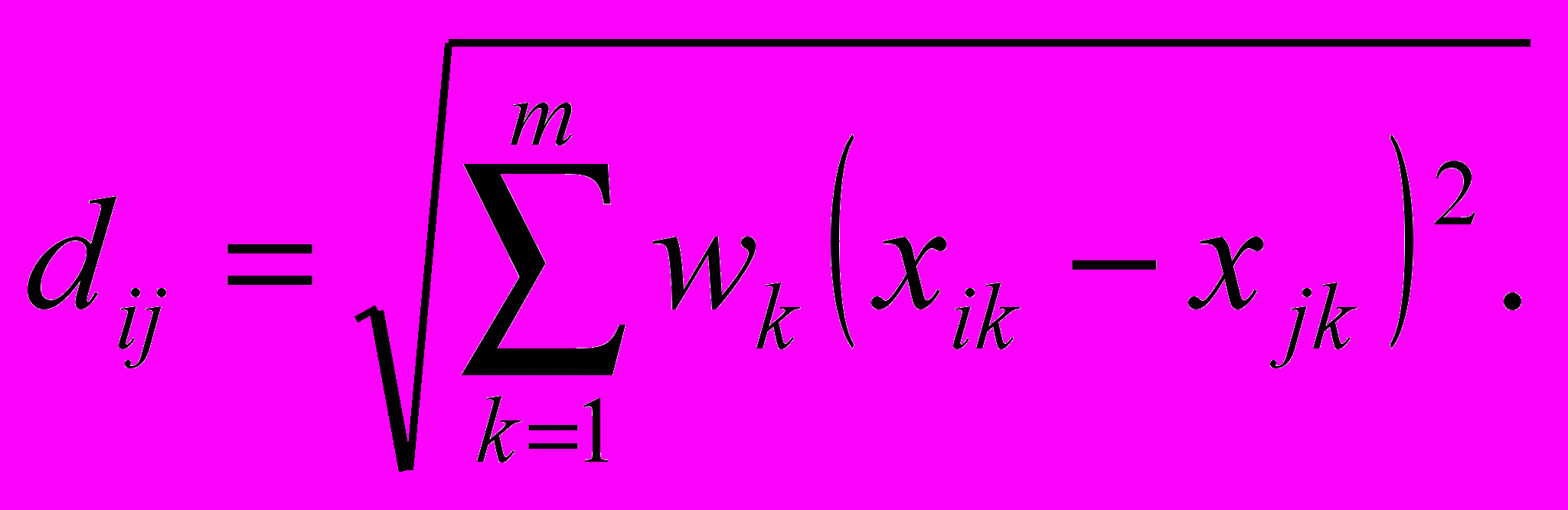(2.2)

где d_ij – расстояние между i-м и j-м объектами; x_ik , x_jk – значения k-й переменной соответственно у i-го и j-го объектов; w_k – вес, приписываемый k-й переменной.

Используются еще расстояние city-blok, расстояние Минковского и Махаланобиса, но в дипломной работе будет использован квадрат евклидового расстояния.

Наравне с различными расстояниями, существуют различные методы кластерного анализа. Это и метод ближнего и дальнего соседа, метод средней связи, метод медианой связи, центроидный, метод Уорда, метод К - средних и другие. В дипломной работе будет использован метод Уорда.

Данный иерархический метод предполагает, что на первом шаге каждый кластер состоит из одного объекта. Первоначально объединяются два ближайших объекта. Для них определяются средние значения каждого признака, и рассчитывается сумма квадратов отклонений :

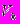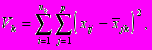(2.3)

где k – номер кластера,

i – номер объекта,

j – номер признака,

p – количество признаков, характеризующих каждый объект,

n_k – количество объектов в k-м кластере.

В дальнейшем на каждом шаге работы алгоритма объединяются те объекты или кластеры, которые дают наименьшее приращение величины 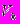. Метод Уорда приводит к образованию кластеров приблизительно равных размеров с минимальной внутри кластерной вариацией. В итоге все объекты оказываются объединенными в один кластер. Алгоритм иерархического кластерного анализа будет проведен со следующей последовательностью процедур.

Шаг 1. Значение исходных переменных нормируются.

Шаг 2. Рассчитывается матрица расстояний или матрица мер сходства.

Шаг 3. Находится пара самых близких кластеров. По выбранному алгоритму объединяются эти два кластера. Новому кластеру присваивается меньший из номеров объединяемых кластеров.

Шаг 4. Процедуры 2, 3 и 4 повторяются до тех пор, пока все объекты не будут объединены в один кластер или до достижения заданного “порога” сходства.

После завершения процедур классификации необходимо оценить полученные результаты. Для этой цели используется некоторая мера качества классификации, которую принято называть функционалом или критерием качества. Наилучшим по выбранному функционалу следует считать такое разбиение, при котором достигается экстремальное (минимальное или максимальное) значение целевой функции – функционала качества.

После кластерного анализа будет проведен корреляционный и регрессионный анализ.

Корреляционный и регрессионный анализ являются смежными разделами математической статистики и предназначены для изучения по выборочным данным статистической зависимости ряда величин, некоторые из которых являются случайными. При статистической зависимости величины не связаны функционально, но как случайные величины заданы совместным распределением вероятностей. Исследование взаимозависимости случайных величин приводит к теории корреляции как к разделу теории вероятностей и корреляционному анализу как к разделу математической статистики. Исследование зависимости случайной величины от ряда неслучайных и случайных величин приводит к модели регрессии и регрессионному анализу на базе выборочных данных. Теория вероятностей и математическая статистика представляют как бы инструменты для изучения статистической зависимости, но не ставят своей целью установление причинной связи.

Формально корреляционная модель взаимосвязи системы случайных величин Х= (х1, х2, ... , хn) может быть представлена в виде: x= f(x,z), где Z - набор внешних случайных величин, оказывающих влияние на изучаемые случайные величины. В работе будет рассмотрена зависимость между доходом отдельно взятого цирка и влияющими на нее факторами. Для статистического анализа с помощью ППП “Статистика” была сформулирована задача, в соответствии с которой, будет проанализирована зависимость доходов от факторов:

• количества мест в цирке;
  
• расходов;
  
• посещаемости.
  

Корреляционный анализ является одним из методов статистического анализа взаимозависимости нескольких признаков.

Выборка представляет собой n независимо наблюдаемых k-мерных точек (векторов): (xi1, xi2, ... , xij, ... ,xik), i= 1n.

Каждая координата xij наблюдаемой точки является вариантом соответствующего признака xj (j=1k) генеральной совокупности, изучаемой с точки зрения взаимозависимости k-признаков. Каждый из признаков является случайной величиной.

В работе в качестве одного из основных показателей взаимозависимости между случайными величинами, используется парный коэффициент корреляции, который служит мерой линейной статистической зависимости между случайными величинами. Его используют, когда статистическая связь между статистическими признаками в генеральной совокупности линейна. То же самое касается частных и совокупных коэффициентов корреляции. Одним из требований, определяющих корреляционный метод, является требование линейности статистической связи, то есть линейности всевозможных уравнений (средней квадратической) регрессии.

Указанные условия выполняются, если генеральная совокупность распределена по многомерному нормальному закону.

В настоящее время корреляционный анализ (корреляционная модель) определяется как метод, применяемый, когда данные наблюдений можно считать случайными и выбранными из генеральной совокупности, распределенной по многомерному нормальному закону.

Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной совокупности по выборке. Для значимых парных коэффициентов имеет смысл указать более предпочтительные точечные и интервальные оценки.

Далее следует оценить и проверить значимость множественных коэффициентов корреляции и детерминации всевозможных подсистем системы xj (j=1k), содержащих три и более случайных величины xj.

Таким образом, основная задача позволяет оценить природу взаимосвязи наблюдаемых переменных.

Дополнительная задача корреляционного анализа (являющаяся основой регрессионного анализа) состоит в оценке уравнений регрессии, где в качестве результативного признака выступает признак, являющийся признаком других признаков (факторов) - причин. Причинно-следственная связь устанавливается из вне статистических соображений, например из аргументов, касающихся физической природы явлений.

Иногда имеет смысл оценить уравнение регрессии для измерения результативного признака по факторным, несмотря на то, что причинно-следственной связи между ними не существует. Здесь причиной могут быть иные факторы, не рассматриваемые в модели, но действующие как на функцию, так и на аргументы уравнения регрессии. Так следует поступать, когда непосредственное измерение результативного признака затруднительно; но существует тесная корреляционная связь (коэффициент множественной корреляции достаточно близок к 1) между результативными и факторными признаками, измерять, наблюдать которые легче в последующих исследованиях. Существуют следующие основные параметры линейной связи между случайными величинами, подлежащих оценке в корреляционном анализе.

В работе будут использованы:

Частный коэффициент корреляции численные значения, которого, могут быть рассчитаны с помощью формулы:

ij/1, 2, ... , i-1, i+1, ... ,j-1, j+1, ... , k= -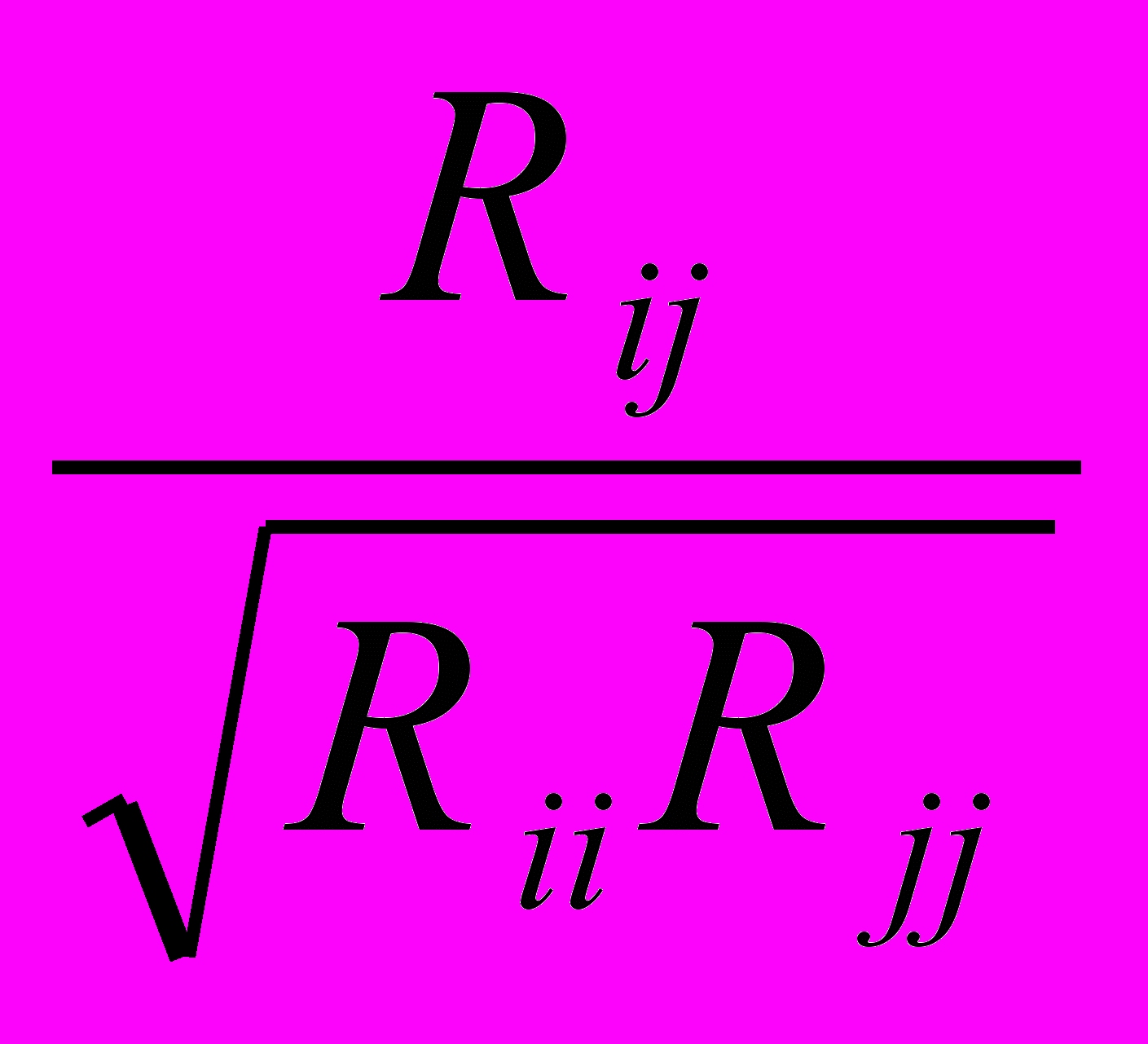. (2.4)

где Rij - алгебраическое дополнение к элементу корреляционной матрицы, расположенному на пересечении i-той строки и j-того столбца.

Целесообразно использовать множественный коэффициент корреляции численные значения, которого, могут быть рассчитаны с помощью формулы (2.5):

i=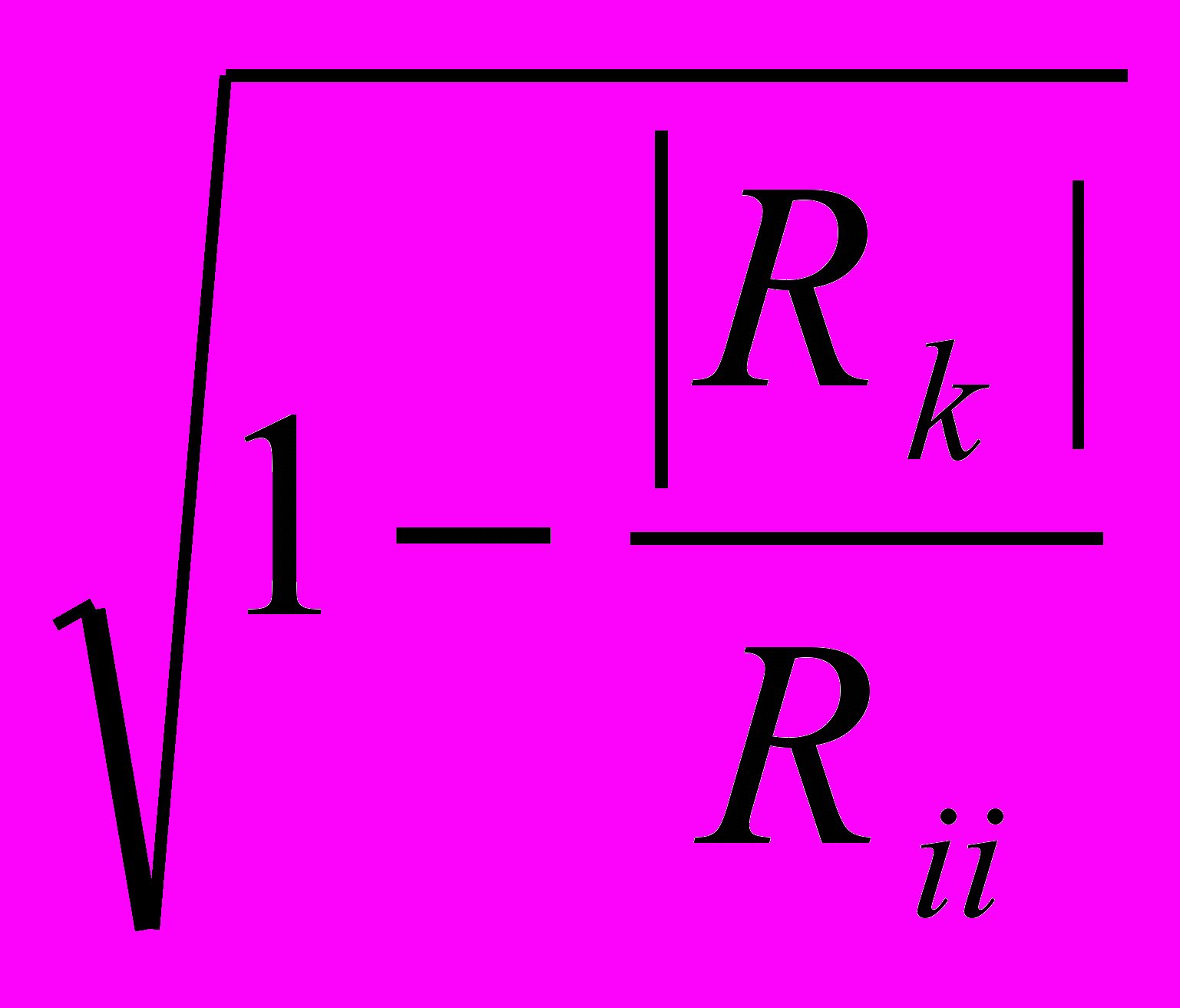, (2.5)

где Rk- определитель матрицы Rk.


Для проверки значимости частных коэффициентов корреляции различных порядков используется тот же критерий, по которому проверяется значимость частного коэффициента нулевого порядка, то есть с использованием величины t, которая подчиняется закону t-распределения Стьюдента. Но число степеней свободы теперь будет равно =n - l - 2, где n - число наблюдений, l - число фиксированных переменных.

tнабл= , (2.6)

где rчастн - соответствующий выборочный частный коэффициент корреляции.

С помощью таблицы распределения Стьюдента на уровне значимости  и с числом степеней свободы =n - l - 2 находят tкр. При tнабл  tкр гипотеза Н0: част=0 отвергается.

Проверка значимости множественного коэффициента корреляции (точнее, коэффициента детерминации) осуществляется с помощью F-распределения Фишера.

С помощью таблицы F-распределения Фишера на уровне значимости , с числом степеней свободы 1= l и 2= n- l -1 находят Fкр. При Fнабл  Fкр гипотеза отвергается.


Для значимых коэффициентов детерминации можно получить более предпочтительные оценки (точечные), чем выборочные коэффициенты:

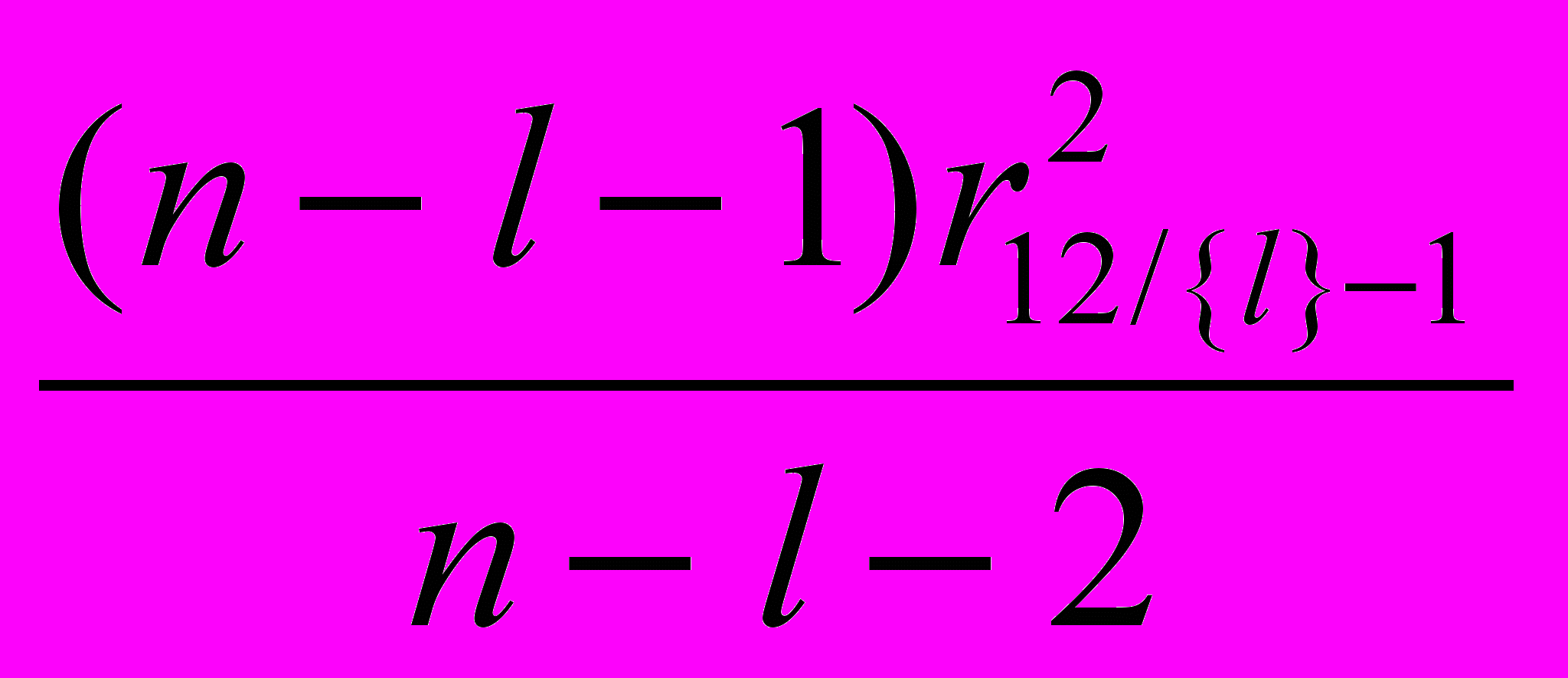- оценка для 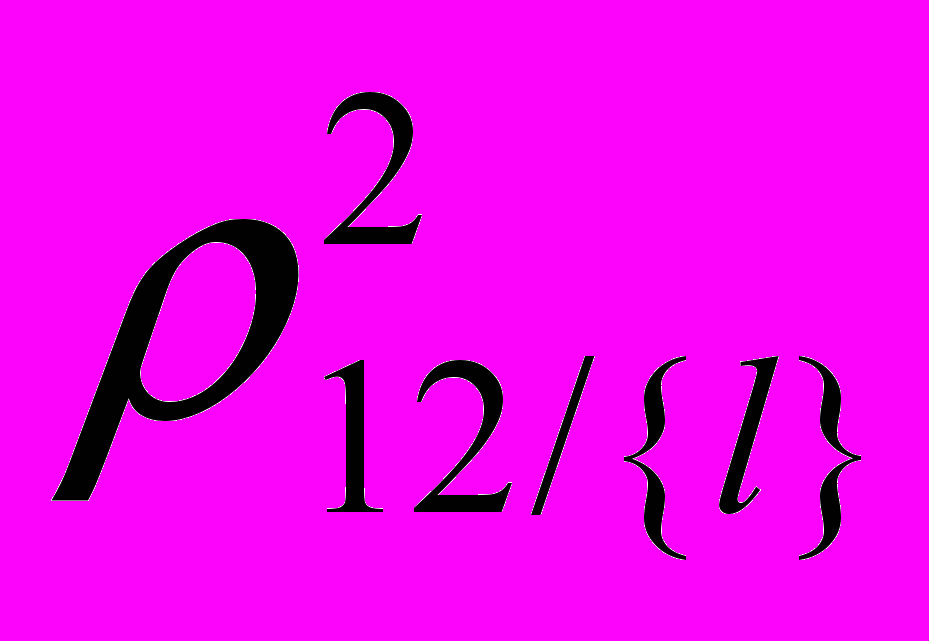, (2.7)

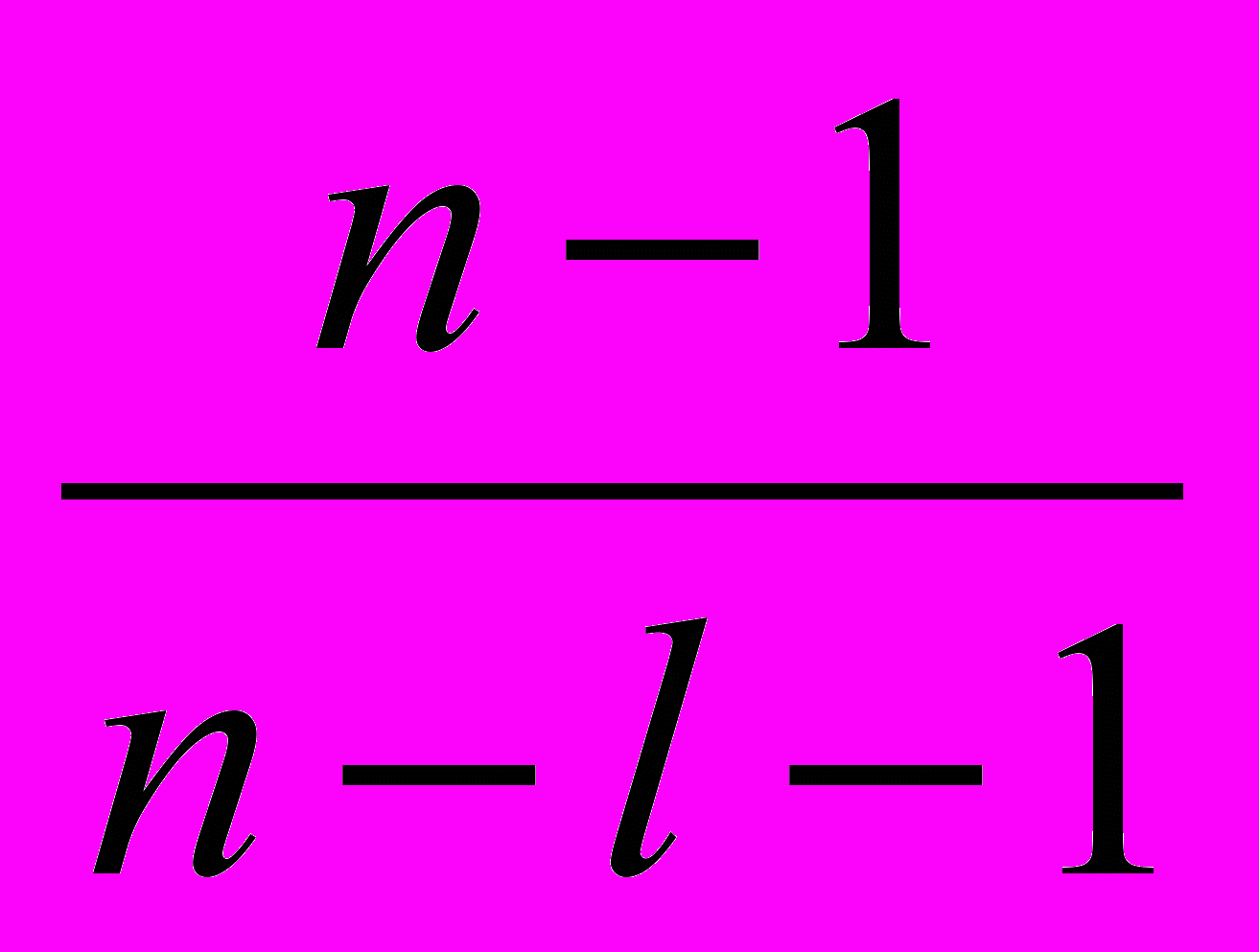- оценка для . (2.8)

Оценку уравнения регрессии и его коэффициентов при достаточно больших k удобнее производить по методике регрессионного анализа.

Анализ всевозможных коэффициентов корреляции (детерминации), как указывалось выше, позволяет оценить природу зависимости между наблюдаемыми переменными. В результате можно определить некоторые признаки, имеющие слабую взаимосвязь с остальными, или включить в систему дополнительные, ранее не учитываемые признаки. Оценка корреляционной матрицы может служить исходным материалом для различных моделей многомерного статистического анализа.

С помощью регрессионного изучается зависимость случайной величины у от некоторого множества переменных x1, x2, ... , xk и неизвестных параметров j (j=0, 1, 2, ... , k). Будем рассматривать (у, x1, x2, ... , xk) как (k+1)-мерную генеральную совокупность, из которой взята случайная выборка объемом n, где (уi, xi1, xi2, ... ,xik) - результат i-того наблюдения, i=1, 2, ... , n. Требуется по результатам наблюдений оценить неизвестные параметры j, j=0, 1, 2, ... , k. Описанная выше задача относится к задачам регрессионного анализа.

Главной предпосылкой построения регрессионной модели является нормальность распределения всех факторов включаемых в модель.

Требование нормального закона распределения у необходимо для проверки значимости уравнения регрессии и его параметров _j, а также для интервального оценивания _j. Для получения точечных оценок _j (j= 0, 1, 2, ... , k) этого условия не требуется.

В общем виде линейная модель регрессионного анализа имеет вид:

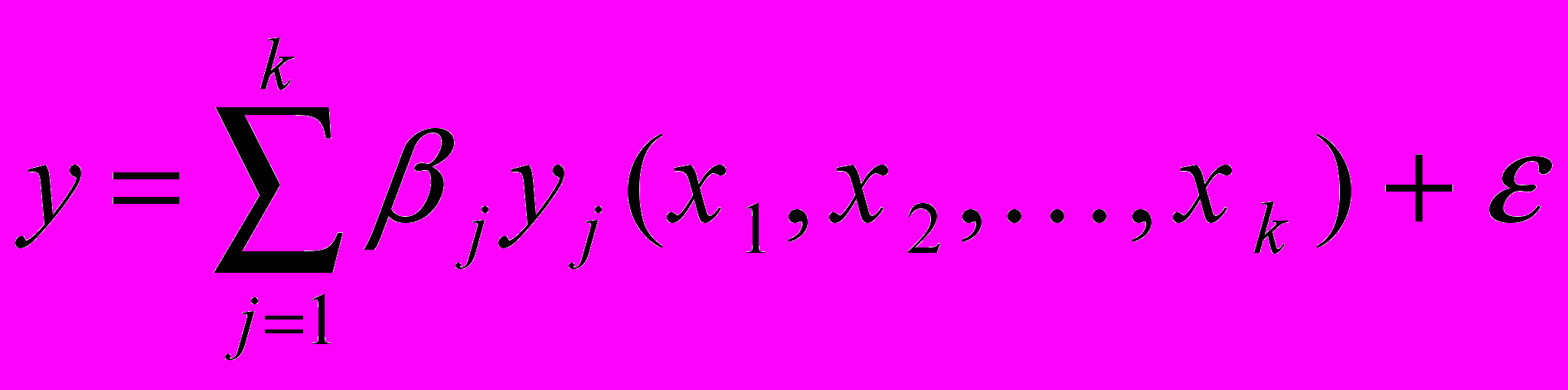, (2.9)

где у_j - некоторая функция от переменных x1, x2, ... , xk;  - случайная величина с математическим ожиданием и дисперсией ².

В регрессионном анализе под линейной моделью подразумевают модель, линейно зависимую от неизвестных параметров _j.

Случайной называется модель, линейно зависимая как от параметров _j, так и от переменных xj.

В регрессионном анализе вид уравнения регрессии выбирают исходя из анализа физической сущности изучаемого явления и результатов наблюдения.

Наиболее часто встречаются следующие виды уравнений регрессии:

• простое линейное 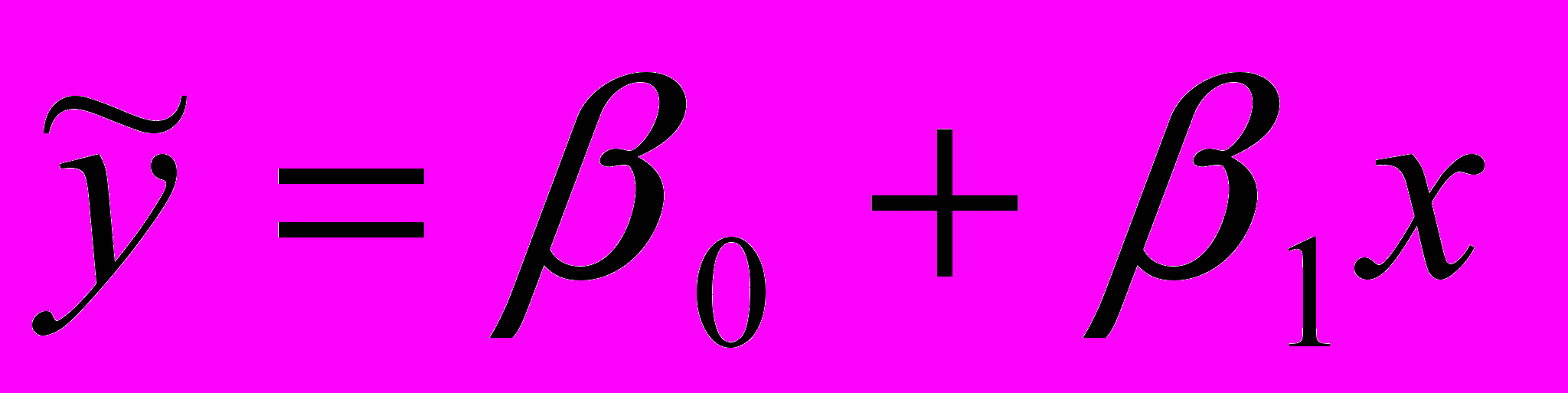; (2.10)
  
• полиномиальное 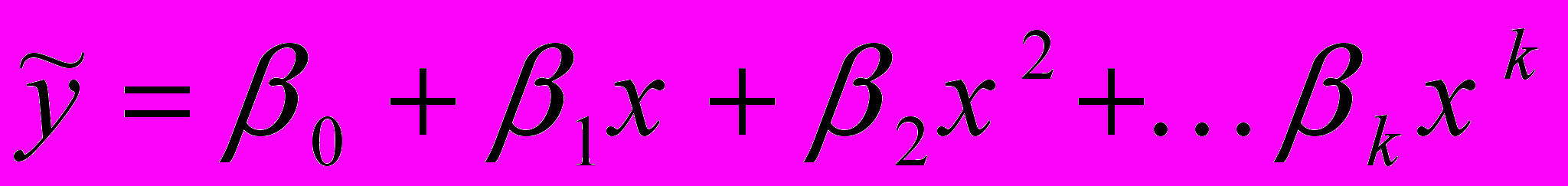; (2.11)
  
• гиперболическое 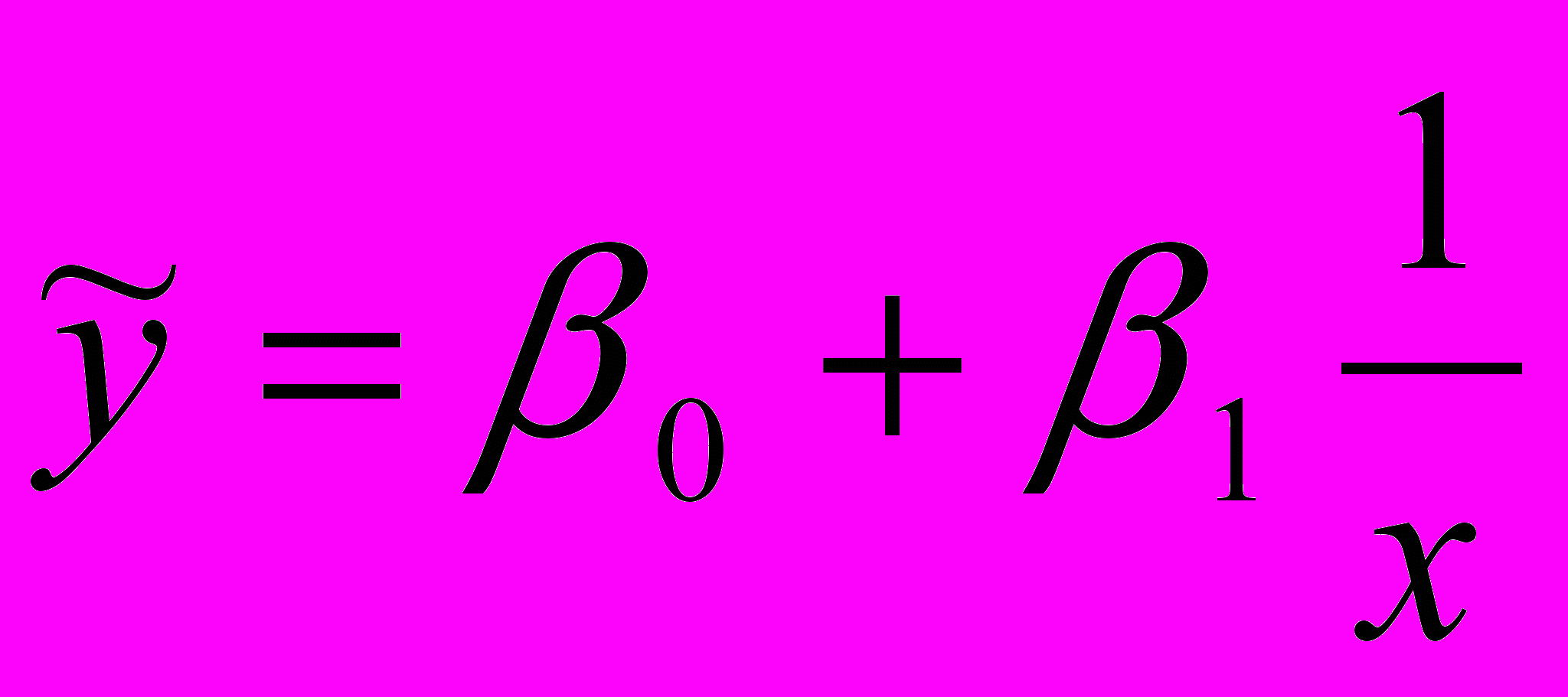; (2.12)
  
• собственно-линейное 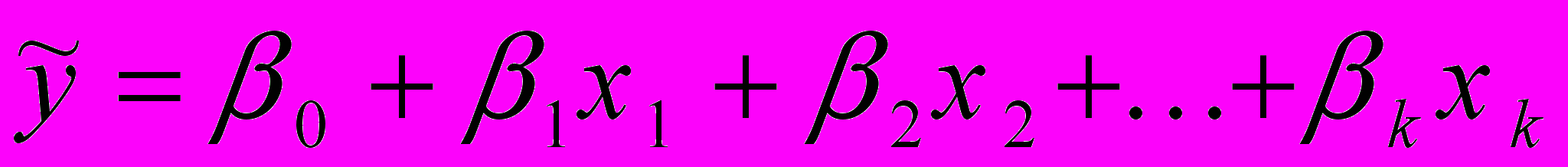; (2.13)
  
• степенное 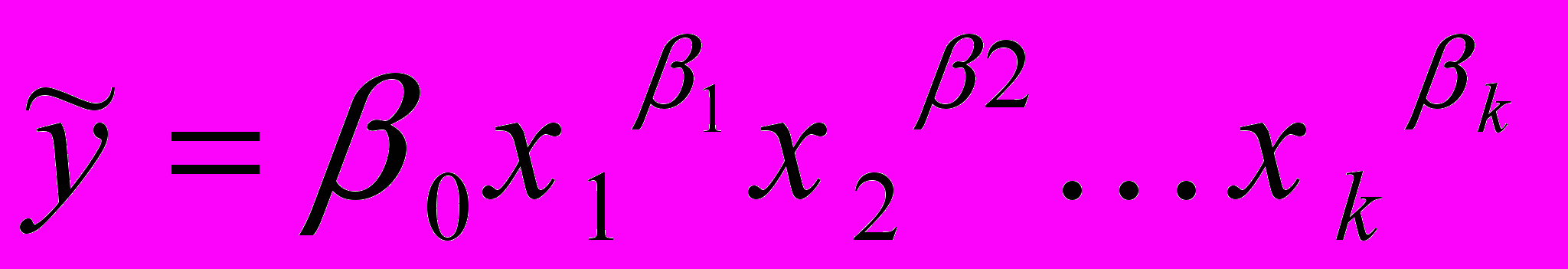. (2.14)
  

Несмотря на то, что существуют различные виды уравнений, для построения многомерной регрессионной модели предпочтение на практике отдается собственно-линейному уравнению. Для оценки параметров собственно линейной регрессионной модели целесообразно использовать метод наименьших квадратов. Оценки получаются не смещенные, состоятельные и асимптотически эффективные.

В дипломной работе будет использована собственно- линейная модель:

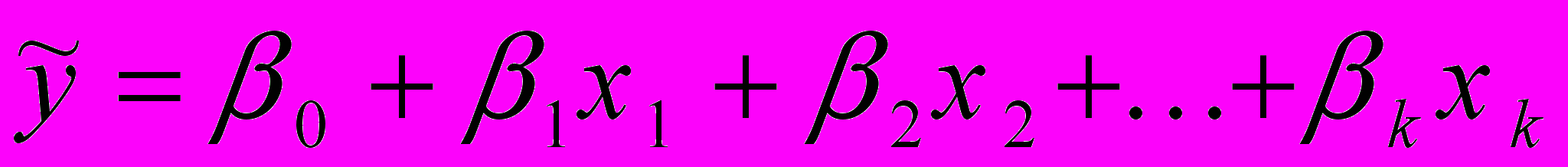. (2.15)

При построении многомерной регрессионной модели существуют ряд проблем, которые должны быть рассмотрены применительно к конкретным статистическим задачам.

Мультиколлиниарность наиболее часто встречаемая проблема, которая заключается в сильной корреляционной связи между независимыми переменными.

Мультиколлинеарность затрудняет проведение анализа, по крайней мере, по трем причинам:

• усложняется процесс выделения наиболее существенных факторов - так как влияние аргумента на функцию, определяющееся по величине β - коэффициента, теряет свою силу;
  
• искажается смысл коэффициентов регрессии при их экономической интерпретации;
  
• возникают осложнения, появляется эффект слабой обусловленности матрицы системы нормальных уравнений, то есть близость ее определителя к 0. В этом случае получается неопределенное множество оценок коэффициентов регрессии b_j.
  

Мультиколлинеарность составляет проблему только в том случае, если она влияет на ту часть множества независимых переменных, которая оказывает наибольшее влияние в анализе на зависимую переменную. В отношении этих переменных необходимо получить дополнительную информацию, состоящую в использовании некоторых субъективных оценок, дополнительном сборе исходных данных, в применении оценок, полученных в аналогичных исследованиях.

Решение проблемы мультиколлинеарности можно разбить на 5 этапов:

• установление факта существования мультколлинеарности;
  
• измерение степени мультколлинеарности;
  
• определение области мультколлинеарности на множестве независимых переменных;
  
• установление причин мультколлинеарности;
  
• определение мер по ее устранению.
  

Существует несколько методов выявления мультколлинеарности. Самый распространенный метод основан на анализе коэффициентов корреляции. Несколько переменных признаются коллинеарными или мультколлинеарными, если парные коэффициенты корреляции между ними больше определенной, ранее заданной, величины. На практике считается что если парный коэффициент корреляции между двумя аргументами по абсолютной величине больше 0.8, то присутствует коллинеарность. Этот метод имеет свои недостатки: он никак не обоснован теоретически, а также отсутствие высоких парных коэффициентов корреляции не свидетельствует об отсутствии мультиколлинеарности.

Для устранения мультиколлинеарности нужно использовать следующие методы:

• методы, основанные на исключении из модели одного или нескольких линейно связанных аргументов или включение в модель только некоторых из переменных, отобранных на стадии экономико-статистического анализа;
  
• методы, основанные на преобразовании данных.
  

Для проверки значимости уравнения регрессии традиционно используют f-критерий, основанный на разложении общей суммы квадратов отклонений на составляющие части:

Q_общ= Q_R+Q_ост, (2.16)

где Q_R= (хb)^т(хb)= 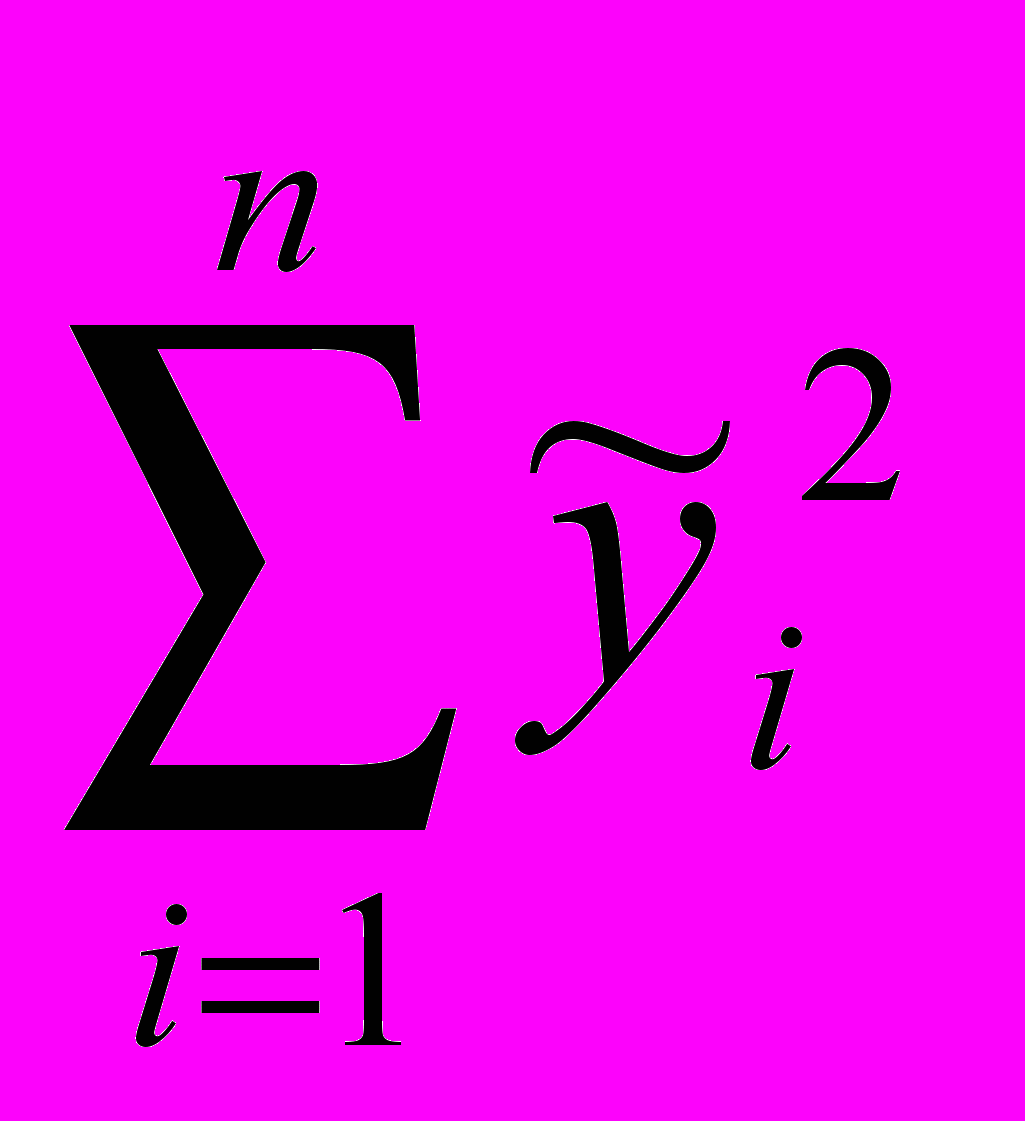- сумма квадратов отклонения от 0, обусловленных регрессией; Q_ост= (y - xb)^т(y - xb)= 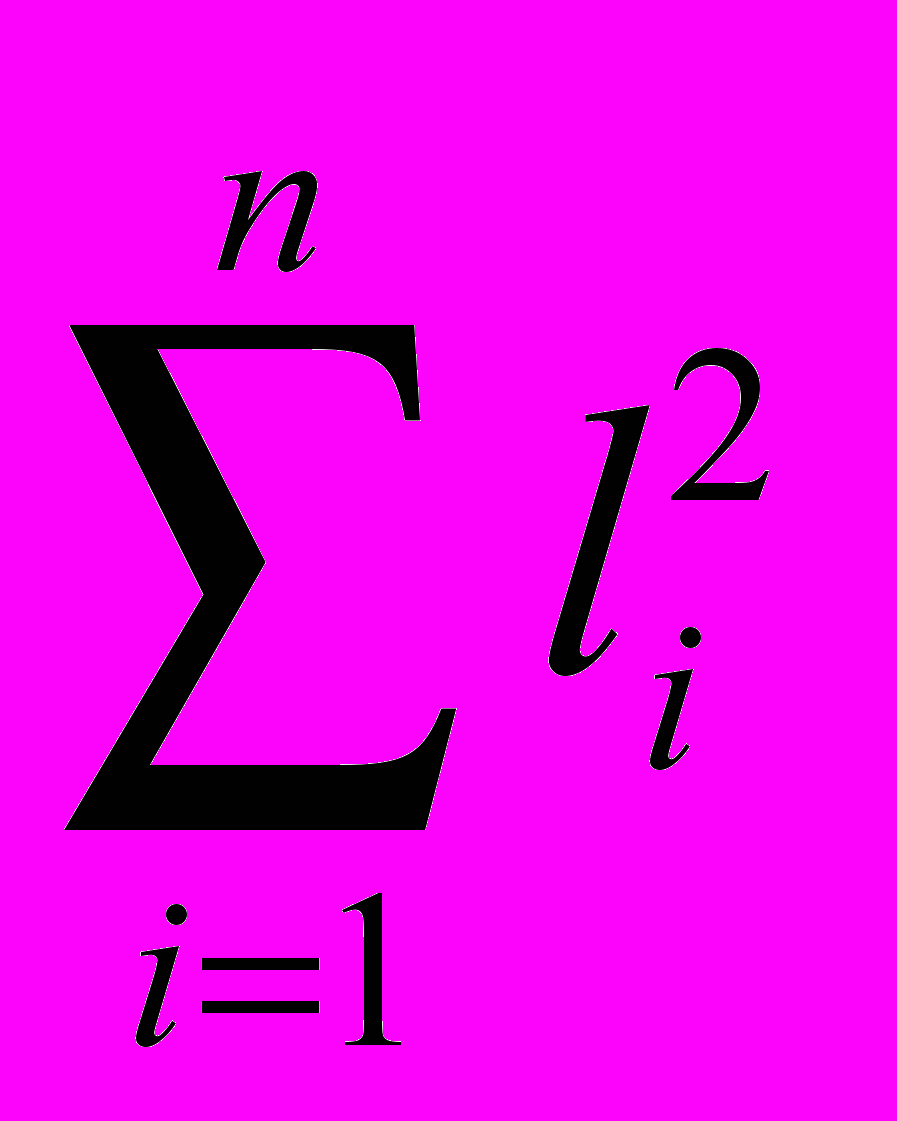- сумма квадратов отклонений фактических значений зависимой переменной от расчетных 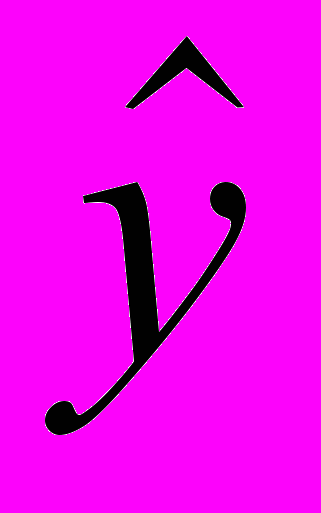=xb, то есть сумма квадратов отклонений относительно плоскости регрессии, обусловленная воздействием случайных и неучтенных в моделях факторов.

Q_общ= у ^ту= 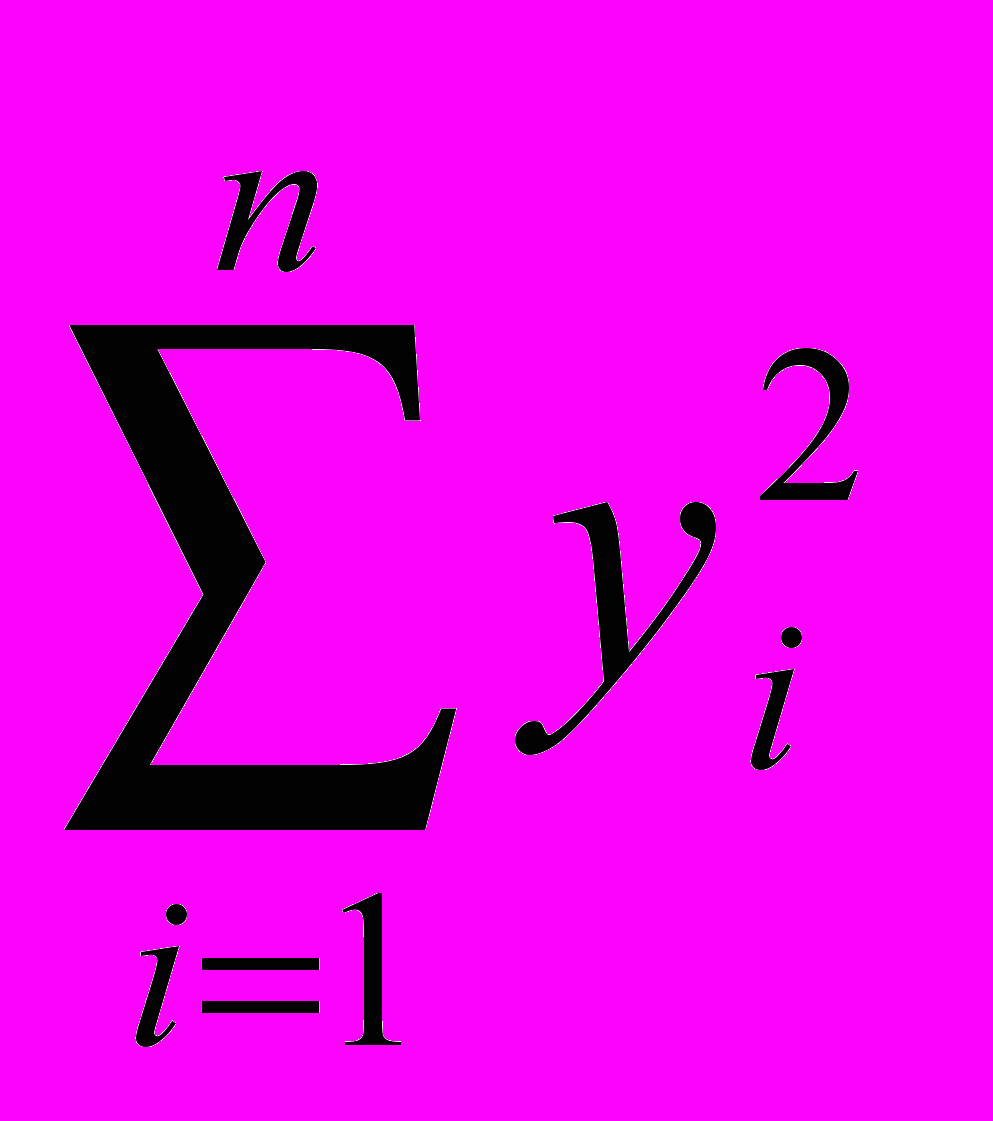- сумма отклонений у_i от 0. (2.17)

Для проверки гипотезы H₀: =0 используется величина:

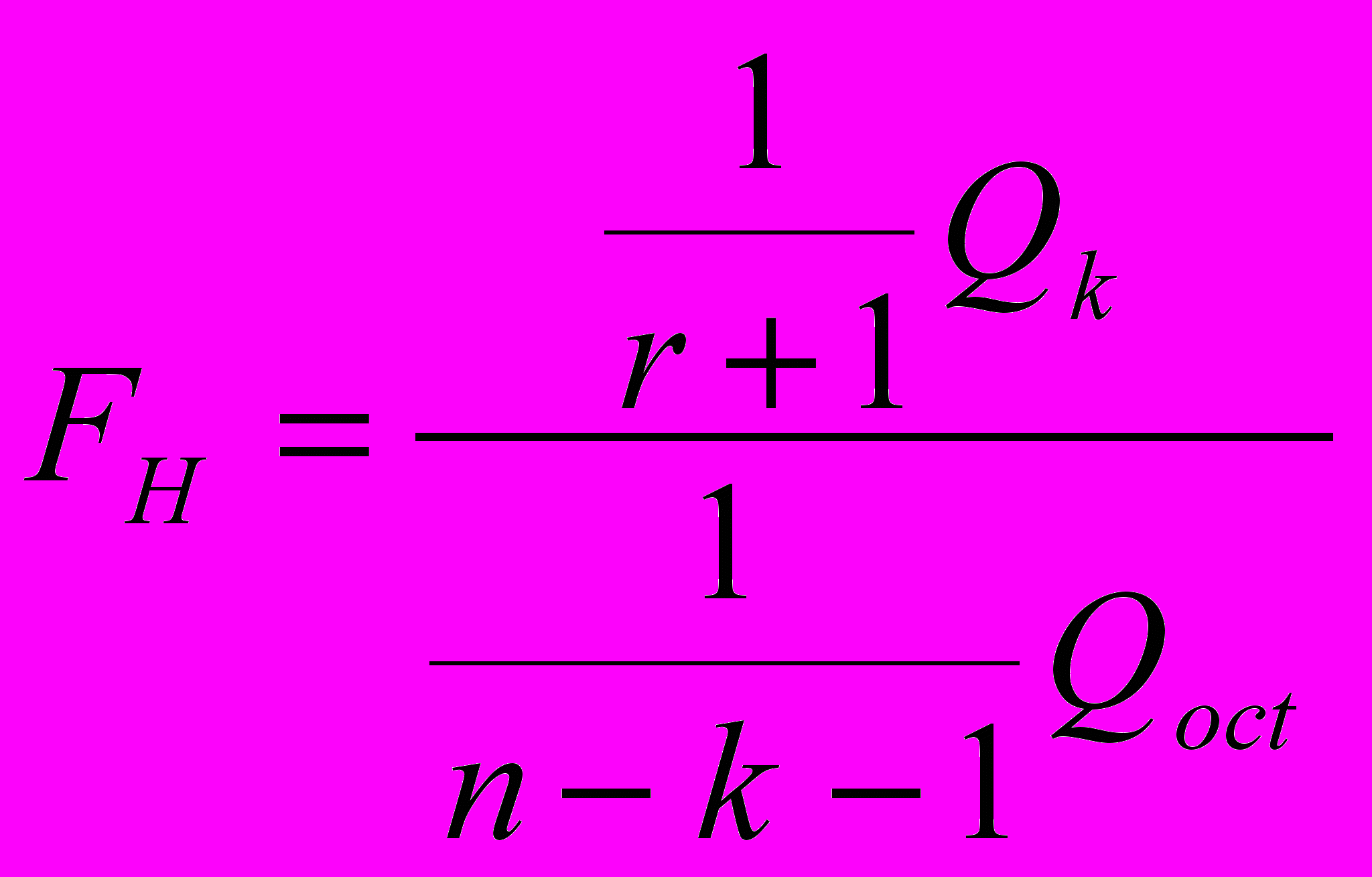, (2.18)

которая имеет f-распределение Фишера-Снедекора с числом степеней свободы ₁=k+1 ₂=n -k -1. Если Fнабл  Fкр(, k+1, n-k-1), то гипотеза H₀: =0 отвергается, значит, уравнение регрессии значимо. Это означает, что в уравнении регрессии есть хотя бы один коэффициент регрессии, отличный от 0.

Если уравнение регрессии незначимо, то есть все коэффициенты уравнения регрессии равны 0, то на этом анализ уравнения регрессии заканчивается.

В случае значимости уравнения регрессии проверяется значимость отдельных коэффициентов регрессии. Для проверки нулевой гипотезы H₀: _j=0 используется величина:

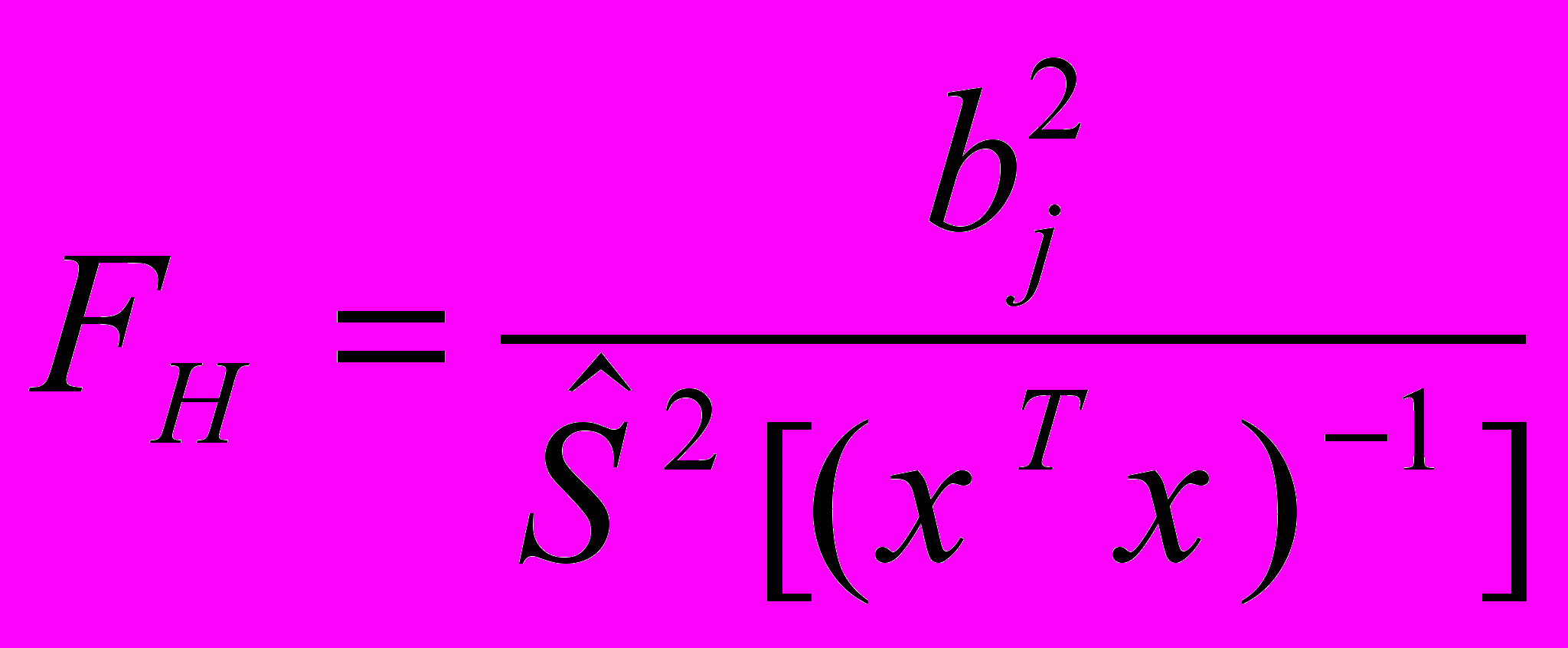, (2.19)

которая имеет f-распределение Фишера-Снедекора с числом степеней свободы ₁=1 и ₂=n -k -1.

Коэффициент регрессии считается значимым, если Fнабл  Fкр(, 1, n-k-1).

Доверительные интервалы для параметров линейной модели.

Для значимых коэффициентов регрессии можно построить доверительные интервалы, используя формулу:

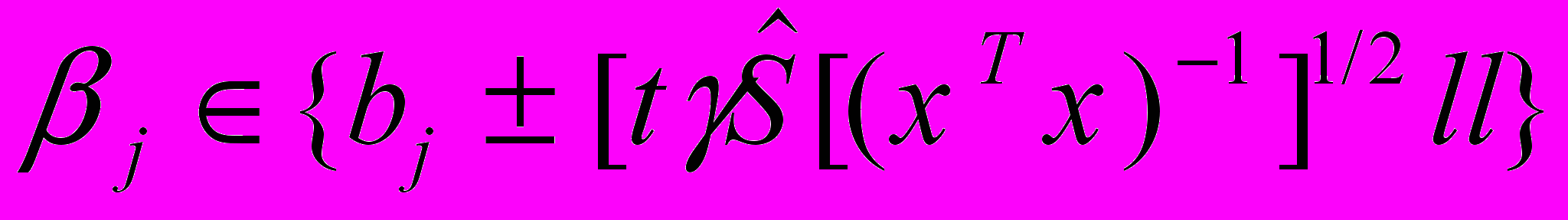, (2.20)

где t находят по таблице распределения Стьюдента для значимости =1- и числа степеней свободы =n-k-1.

Интервальная оценка 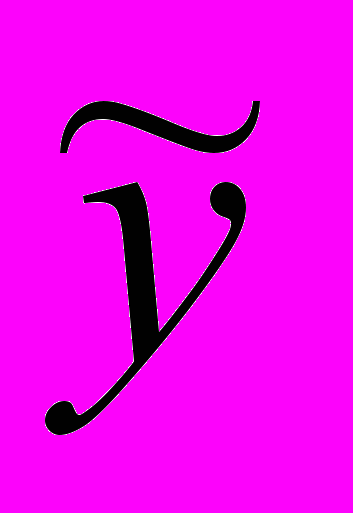в точке, определяемой вектором начальных условий х⁰, определяется по формуле:

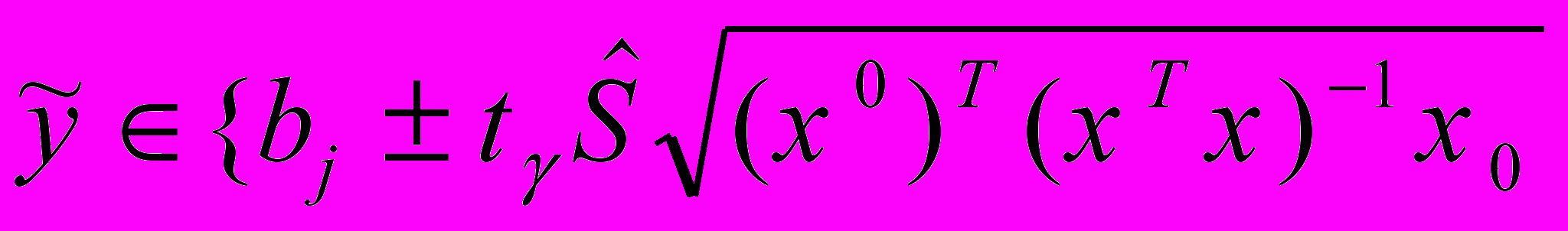, (2.21)

где 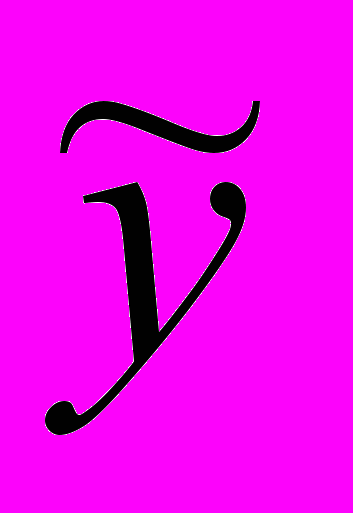= (x⁰)^тb;

x⁰= 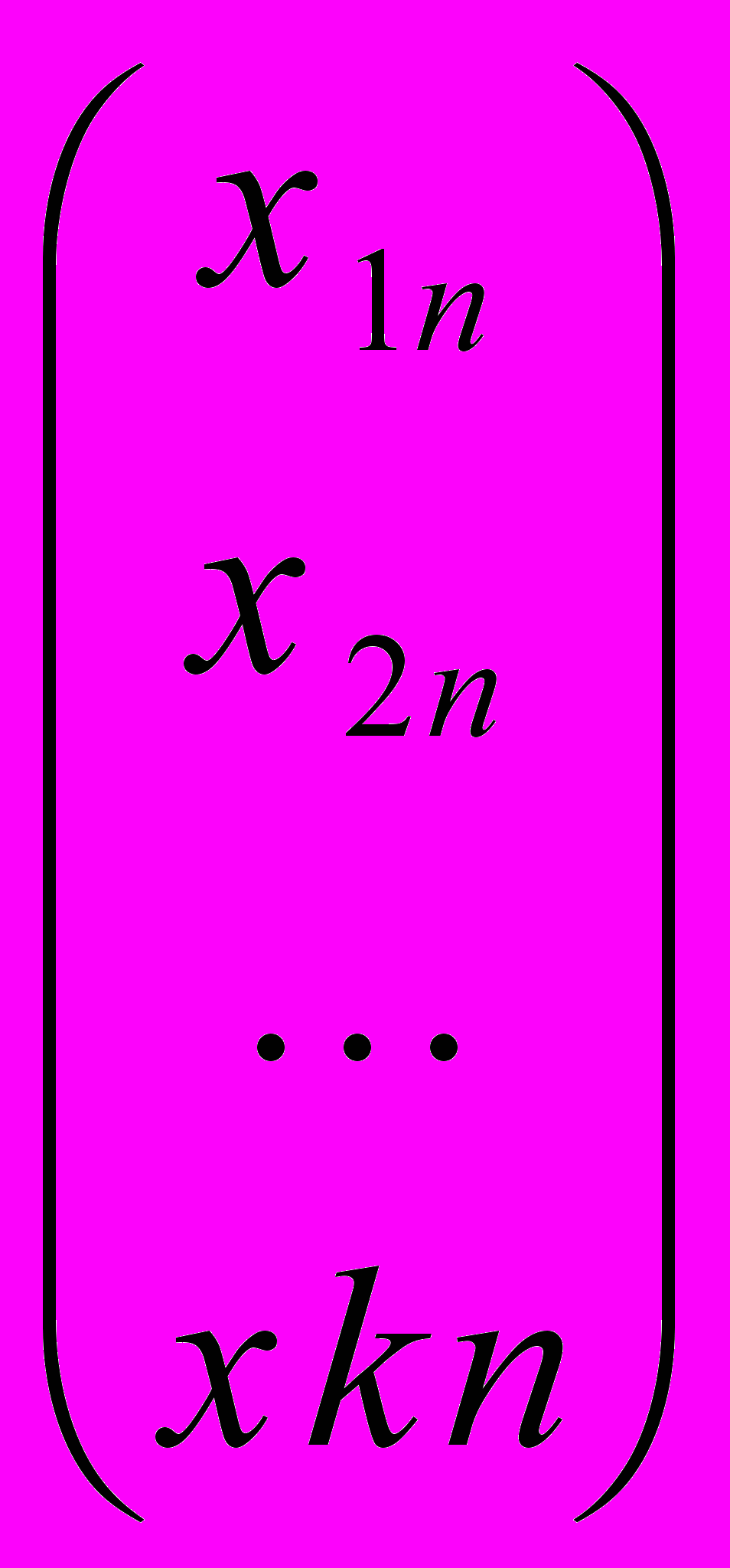- вектор-столбец начальных условий размерности (k+1)

t определяется по таблице распределения Стьюдента для уровня значимости  и числа степеней свободы =n -k -1.

Для построения модели будет использован метод пошаговой регрессии. Сложность взаимосвязи факторов в модели, характеризующих экономические явления, необходимо упростить с целью выделения наиболее существенных связей. Нужно найти оптимальный вариант модели, отражающий основные закономерности исследуемого явления с достаточной степенью статистической надежности. В модель должны быть включены все факторы, которые с экономической точки зрения оказывают влияние на зависимую переменную, однако, количество факторов, включаемых в модель, не должно быть очень большим. Невыполнение этого условия приведет к ряду затруднений, среди которых - снижение точности оценок, сложность интерпретации модели и трудности ее практического использования.

Можно выделить два различных подхода к решению проблемы сокращения количества исходных переменных. Один из них основывается на том, что отсеиваются менее существенные факторы в процессе построения исходной модели, а второй - на замене исходного набора переменных меньшим числом эквивалентных факторов, полученных в результате преобразований исходного набора.

Процедура отсева несущественных факторов в процессе построения регрессионной модели получила название многошагового регрессионного анализа. Этот метод основан на вычислении нескольких промежуточных уравнений регрессии, в результате анализа которых получают конечную модель, включающую только оказывающие тесное статистически существенное влияние факторы на исследуемую зависимую переменную.

В данной задаче мною использовался многошаговый регрессионный анализ, основанный на оценке значимости коэффициентов регрессии с помощью t-критерия Стьюдента. Уравнение регрессии строится по максимально возможному количеству объясняющих переменных, предположительно влияющих на исследуемую переменную. После этого с помощью определенных критериев исключают те переменные, которые оказывают статистически несущественное влияние. Схема отбора значимых факторов в уравнении регрессии с помощью t-критерия выглядит так: если все коэффициенты регрессии значимы, то уравнение регрессии признается окончательным и принимается в качестве модели исследуемого признака; если среди коэффициентов регрессии имеются незначимые, то соответствующие объясняющие переменные следует исключать из уравнения. Однако предварительно следует проранжировать коэффициенты регрессии по величине t_набл и в первую очередь исключить такой фактор, для которого коэффициент регрессии незначим и t_набл имеет наименьшее значение по абсолютной величине. Значение уравнения регрессии пересчитывается снова без исключенного фактора и затем производится оценка коэффициентов регрессии по t-критерию. Это повторяется до тех пор, пока коэффициенты регрессии в уравнении не станут значимыми.

Простейшая схема проверки значимости коэффициентов регрессии сводится к построению доверительного интервала для каждого из них и проверки гипотезы о том, находится ли ноль в внутри построенного интервала. Если гипотеза не отвергается, то этот коэффициент регрессии считается незначимым или его значимость подвергается сомнению и выясняется на следующих этапах анализа. При данном методе на каждом шаге, кроме формальной статистической проверки значимости коэффициентов регрессии, поводится также экономический анализ несущественных факторов и устанавливается порядок их исключения. В некоторых случаях значение t_набл находится вблизи t_кр, и с точки зрения содержательности модели этот фактор можно оставить для последующей проверки его значимости в сочетании с другими наборами факторов. Не существенность коэффициента регрессии по t-критерию не всегда является основанием для исключения переменной из дальнейшего анализа. Поэтому в некоторых случаях нужно использовать некоторые дополнительные эмпирические процедуры исключать переменную из уравнения регрессии лишь в том случае, когда средняя квадратическая ошибка коэффициента регрессии превышает абсолютный размер вычисленного коэффициента, когда t_набл1.5.


3. Построение многомерной регрессионной модели дохода для цирков Российской Федерации.

3.1 Выбор факторов для построения многомерной регрессионной модели дохода цирков Российской Федерации.

Для построения многомерной регрессионной модели доходов цирков Российской Федерации были выбраны цирки 34-х городов РФ. На основании статистических данных предоставленных Росгосцирком и Госкомстатом РФ был проведен предварительный анализ исходных данных. В качестве факторов характеризующих деятельность цирков, были рассмотрены: население города, количество мест в цирке, количество представлений, количество зрителей, посетивших цирк, доходы, расходы, прибыль и посещаемость. Для получения однородной статистической совокупности был проведен кластерный анализ, в результате которого были получены кластеры, обладающие достаточной статистической однородностью для построения многомерной регрессионной модели. Кластерный анализ был проведен по 8 показателям, однако для построения многомерной регрессионной модели все эти показатели использованы быть не могут, так как объем выборки должен быть значительно больше числа факторов, включаемых в регрессионную модель n>>k .

Такие факторы как количество зрителей, количество мест и количество представлений входят в формулу расчета численных значений фактора посещение формула (3.1):