Санкт-петербургский государственный политехнический университет

Вид материала

Содержание

Характеристика Компьютерных программ 11
Характеристика методов анализа I. Множественный корреляционно-регрессионный анализ.
Анализ проводить по принципу: от простого к более сложному
Исходные данные
Авторегрессионая модель
II. Факторный анализ
Поиск названий
Исходные признаки
III. Многомерное шкалирование.
IV. Кластерный анализ
Кластерный анализ.
V. Дискриминантный анализ
VII. Метод канонических корреляций
Характеристика Компьютерных программ VII. Компьютерный анализ многомерных статистических данных.
Пакет DSTAT
Факторный анализ (Factor analysis
Пакет DSTAT
Краткая характеристика тем
Тема 9. Использование методов факторного анализа для оценки фондовых рынков.
Среднегодовой индекс, Х
...
Полное содержание

Подобный материал:

1 2 3 4 5 6 7 8 9

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

_____________________________________

Н.И. Диденко

Методы анализа процессов

в мировой экономике

Санкт-Петербург

2007

Содержание

Характеристика методов анализа 3

I. Множественный корреляционно-регрессионный анализ. 3

II. Факторный анализ 4

III. Многомерное шкалирование. 7

IV. Кластерный анализ 8

V. Дискриминантный анализ 9

VII. Метод канонических корреляций 10

Характеристика Компьютерных программ 11

VII. Компьютерный анализ многомерных статистических данных. 11

Краткая характеристика тем 13

Тема 1. Анализ ценообразования на мировом рынке конкретного товара. 13

Тема 2. Моделирование циклических колебаний в мировой экономике. 13

Тема 3. Моделирование циклических колебаний в мировой экономике. 13

Тема 4. Сравнительный анализ модели инвестиций и сбережений по группам стран. 13

Тема 5. Анализ роста ВВП страны за период 1800 2000 гг. 13

Тема 6. Анализ дополнительных возможностей выращивания злаковых культур в странах мира. 14

Тема 7. Ранжирование стран по уровню жизни в зависимости от макроэкономических показателей. 14

Тема 8. Анализ бирж методами многомерного шкалирования. 14

Тема 9. Использование методов факторного анализа для оценки фондовых рынков. 15

Тема 10. Использование метода главных компонент для группировок ТНК. 15

Тема 11. Использование метода главных компонент в корреляционно-регрессионном анализе. 16

Тема 12. Анализ совокупного импорта стран мира методом главных факторов. 16

Тема 13. Анализ совокупного экспорта стран мира методом максимального правдоподобия (факторный анализ). 17

Тема 14. Классификация стран методом кластерного анализа. 17

Тема 15. Сравнение изменения производительности труда от факторов в различных группах стран. 17

Тема 16. Классификация стран по уровню изменения курса национальной валюты. 18

Тема 17. Анализ сходства международных банков (кластерный анализ). 18

Тема 18. Классификация субъектов федерации РФ/регионов РФ (Сравнение различных алгоритмов классификации). 18

Тема 19. Классификация по методу поиска сгущений. 19

Тема 20. Классификация стран мира. (Иерархический кластерный анализ по алгоритмам «ближайшего соседа» и «дальнего соседа»). 19

Тема 21. Использование дискриминантного анализа. 20

Тема 22. Использование дискриминантного анализа. 20

Тема 23. Дискриминантный анализ фондовых рынков. 20

Тема 24. Метод канонических корреляций. 21

Тема 25. Метод канонических корреляций. 21

Тема 26. Метод канонических корреляций. 21

Тема 27. Анализ мирового фондового рынка 22

Тема 28 Анализ прямых иностранных инвестиций в мировой экономике 23

Тема 29. Анализ тенденций в экономике конкретных стран 25

Характеристика методов анализа

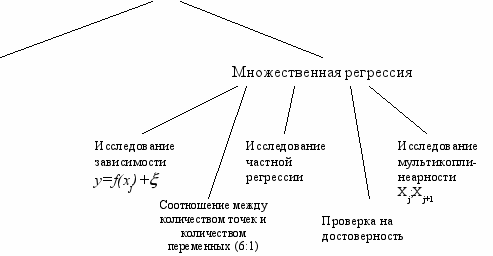
I. Множественный корреляционно-регрессионный анализ.

Множественный корреляционно-регрессионный анализ

Парная корреляция и парная регрессия

Парная корреляция
Частная корреляция
Регрессионная зависимость и её выбор

Уравнение в натуральном масштабе ŷ =XB

Уравнение в стандартизованном виде

Частные и множественные коэффициенты детерминации

Пример моделей приведён в табл.1.

Таблица 1

Наиболее распространенные нелинейные модели

	Нелинейная модель	Преобразование исходных данных для перехода к линейному виду	Описываемые процессы
1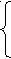.	Полиномиальная ŷ=a₀+a₁x₁+a₂x₂²+…+a_mx_m^m	x₁₁x₁₂²… x_1m^m y=y; x= x₁₂x₂₂²… x_2m^m	Процессы, меняющие направление
2.	Линейно-логарифмическая ŷ=ax₁^a1.x₂^a2…x_m^am	y=lg(y); x=\|\|a_jlgx_ij\|\|
3.	Экспоненциальная ŷ=e ^{a0+a1x1+…+amxm}	y=ln(y); x=x
4.	Сложная экспоненциальная ŷ=1/(1+e ^{a0+a1x1+…+amxm})	y=ln(y^-1-e); x=x
5.	Обратная ŷ=1/(a₀+a₁x₁+a₂x₂²+…+a_mx_m^m)	y=y^-1; x=x

Оценка достоверности полученной модели и её параметрических характеристик.

А. Статистические оценки надежности регрессионной модели в целом:

коэффициент множественной детерминации и корреляции;
средний квадрат модельной ошибки;
коэффициент аппроксимации;
F-критерий Фишера.

В. Статистическая оценка надежности коэффициентов регрессии:

t - критерий Стьюдента

С. Статистические оценки достоверности коэффициентов корреляции:

t - критерий Стьюдента для частных и парных коэффициентов корреляции;
F-критерий Снедекора для коэффициентов множественной детерминации.

Анализ проводить по принципу: от простого к более сложному:

а) рассматривать простейший случай линейной зависимости двух переменных Y и X, где Y зависимая переменная, Х факторная переменная;

b) произвести статистическое оценивание неизвестных параметров регрессионного уравнения b₀ и b₁ (Y= b₀ + b₁Х+U) и дисперсионной ошибки ²;

с) оценить качество регрессионной модели и параметрические значения: b₀, b_1,²;

d) перейти к случаю с любым числом факторных переменных Х;

е) перейти на нелинейные регрессионные модели.

Исходные данные регрессионного анализа могут быть центрированы:

где

средние значения.

Два особых случая регрессионной модели:

1) регрессионная модель не содержит параметра b₀;

2) регрессионная модель содержит один коэффициент регрессии:

Первый случай: Y_i= b₁Х_i+U_i, U_i N(0, ²);

Второй случай: Y_i= b₀ + U_i, U_i N(0, ²);

Авторегрессионая модель

y=Xb+U y_i= bХ_i+U_i

U_i=  U_i-1+_i

Авторегрессионая модель представляет случай коррелированности наблюдений, например, во времени (последующее событие часто зависит от совершения предыдущего).

II. Факторный анализ

Факторный анализ совокупность методов, позволяющих выявить скрытые (латентные) характеристики на основе существующих признаков.

Скрытые (латентные) это неявные характеристики, раскрываемые при помощи методов Ф.А.

Исследуются объекты с набором признаков X_j.

Коррелировать могут не только признаки X_j, но и сами наблюдаемые объекты N_i.

Пример. Исследуем n стран, оцениваемых в двухмерном признаковом пространстве с осями: X₁ ВВП, X₂ стоимость потребительской корзины (рис.1).

Можно ввести новые оси F₁ и F₂, которые проходят через плотные скопления точек и коррелируют с X₁ и X_2.

Допустим, что F₁ = a₁x₁+a₂x₂

F₂ = a₁x₁+a₂x₂

Интерпретируем оси F_N : F₁ уровень жизни; F₂ ВВП на душу населения.

В результате анализа можно выявить классификационные признаки.

Рассмотрим координатное пространство двух стран и признаки x₁, x₂, x₃, x₄, x₅.(рис.2)

Рассматривают

См. книги следующих авторов:

Л. Гуттман, Г. Хотеллинг, Л. Тэрстоун, К. Хользингер, С. Рао, С. Барт, Г. Томсон, Д. Лаули, А. Максвелл, а также

Г. Харман «Современный факторный анализ»………………….

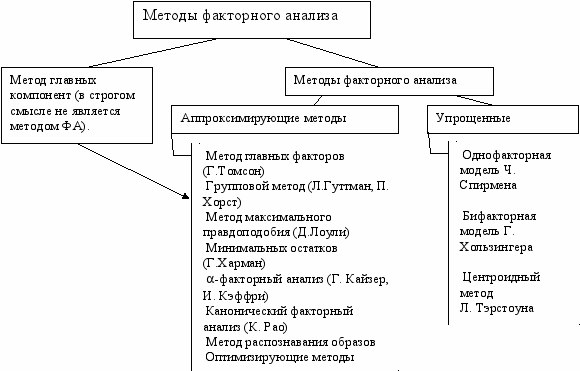
Задача: Известна информация по n объектам с m признаками по объекту. Необходимо перейти от матрицы (nm) к матрице (nr) или (mr), r
Поиск названий для главных компонент.

Задачу распознавания главных компонент, определения для них названий решают субъективно на основе весовых коэффициентов a_jrматрицы А

Дано: x_ij

Преобразована:

Результат поиска главных компонент изложен в табл.2.

Таблица 2

Пример гипотетических данных.

Исходные признаки	Главные компоненты
Х_j	F₁	F₂
x₁ ВВП на душу населения	a₁₁=0.8	a₁₂=0.4
x₂ уровень фондоотдачи в промышленности	a₂₁=0.3	a₂₂=0.7
x₃ численность занятых в промышленности	a₃₁=0.9	a₃₂=0.1
x₄ среднегодовая рентабельность промышл.	a₄₁=0.7	a₄₂=0.2
x₅ индекс промышленного роста цен	a₅₁=0.2	a₅₂=0.6
x₆ уровень энерговооруженности в промышленности	a₆₁=0.1	a₆₂=0.8

Заключение. Метод главных компонент и методы факторного анализа базируются на идее, что связи признаков x₁, x₂, … x_m это результат воздействия сравнительно небольшого числа неявных (латентных, скрытых) факторов F_1,F_{2, …}F_N), (r
Основная задача ФА переход от данных (nm) к (mr) и значений общих факторов (nr).

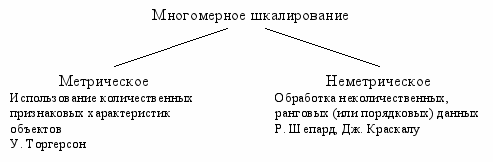
III. Многомерное шкалирование.

Теория многомерного шкалирования предполагает возможность развертывания наблюдаемых объектов в некотором теоретическом пространстве.

Поиск координатного пространства в МШ осуществляется не по значениям признаков, характеризующих объекты, а по данным представляющим различия или сходство этих объектов.

Основным источником данных являются эксперты.

Непосредственно о самом объекте даже по значениям некоторого набора признаков нельзя судить достаточно надежно или полно. Но эксперты ещё до проведения аналитических расчетов видят, интуитивно чувствуют различия изучаемых объектов.

Основным источником данных являются эксперты.

Исходная информация представлена в виде трёх матриц.

I. Матрица условных вероятностей или матрица идентификации (табл. 3)

Таблица 3.

Условные вероятности

	x₁	x₂	x₃	x₄
x₁
x₂
x₃
x₄

Столбцы это объекты, распознанные экспертами.

Строки это перечень объектов, предъявляемых для оценки.

II. Матрица аналитических признаков (табл.4)

Таблица 4

Характеристика объектов

Признак Объект	Оборот капитала, млн.	Прибыль, млн.	Кол-во работ-ников, чел.
Биржа (Чикаго)
Биржа (Индия)
Биржа (СПб)

III. Матрица временных интервалов (табл.5)

Таблица 5

Производительность труда в промышленности стран мира

	1980	1985	1990	1995	2000
РФ
Германия
США
Франция
Корея
КНР

Приемы получения исходных ранговых данных (неметрическое шкалирование) следующие:

Метод последовательной рандомизации
Метод исходной (якорной) точки
Метод рейтинговой оценки

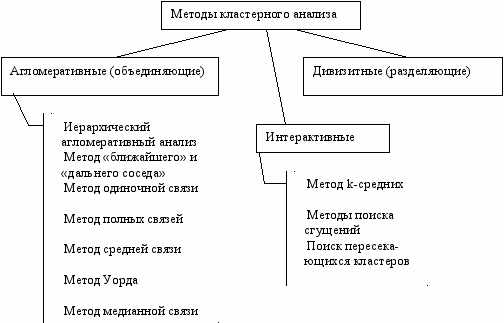
IV. Кластерный анализ

Целью кластерного анализа является образование групп схожих между собой объектов кластеров.

Различие комбинационных группировок и кластерного анализа.

Метод комбинационной группировки.

Наблюдаемый объект характеризуется тремя признаками x₁, x₂, x₃.

Совокупность наблюдаемых объектов разбивается на группы по x₁, а затем внутри каждой выделенной подгруппы по x₂, затем по x₃.
Образованные группы имеют границы по каждому группировочному признаку.

Кластерный анализ.

Все группировочные признаки одновременно участвуют в группировке, т.е. они одновременно учитываются при отнесении объекта в ту или иную группу.

Критерии качества классификации.

Сумма квадратов расстояний до центров классов:

где l номер кластера;

центр l-го кластера;

X_i вектор значений переменных для i-го объекта в l-ом кластере;

расстояние между i-ом объектом и центром l-го кластера.

Сумма внутриклассовых расстояний между объектами:

Суммарная внутриклассовая дисперсия:

где

дисперсия j-ой переменной в кластере S_l

ППП: CLUSTAN

V. Дискриминантный анализ

Дискриминация различение (расчленение) объектов анализа по определенным признакам.

Дискриминантные переменные признаки, используемые для того, чтобы отличить один класс (подмножество) от другого.

Переменные измеряются либо по интервальной шкале, либо по шкале отношений.

Интервальная шкала количественно описывает различия между свойствами объектов. Пример интервальных шкал: календарное время, шкала температур. В качестве оценки положения центра используются средняя величина, мода, медиана.

Шкала отношений частный случай интервальной шкалы. Она позволяет соотнести количественные характеристики какого-то свойства у разных объектов, например, ВВП на душу населения, удельный вес налогов.

Число объектов анализа должно превышать число дискриминантных переменных минимум на два.

Дискриминантные переменные должны быть линейно независимыми.

Основное отличие дискриминантного анализа и кластерного анализа: в ходе дискриминантного анализа новые кластеры не образуются, а формируется правило, по которому новые единицы совокупности относятся к одному из уже существующих множеств (классов).

Дискриминантный анализ можно использовать как метод прогнозирования (предсказания) поведения анализируемых объектов на основе имеющихся стереотипов поведения аналогенных объектов, входящих в состав существующих или сформированных по определенному принципу множеств.

ППП: DSTAT

VII. Метод канонических корреляций

Каноническая корреляция это расширение парной корреляции на случай, когда имеется несколько результативных показателей Y и нескольких факторов X.

В каноническом анализе матрица значений исходных переменных имеет вид (табл. 6).

Таблица 6

Исходные данные в каноническом анализе

Объект анализа	Результативные показатели				Переменные показатели
Объект анализа	Y₁	Y₂	…	Y_p	X₁	X₂	…	X_N
1.	y₁₁	y₁₂	…	y_1p	x₁₁	x₁₂	…	x_1N

…	…	…	…		…		…	…
n	Y_n1	Y_n2	…	Y_np	X_n1	X_n2		X_nN

Метод канонических корреляций позволяет одновременно анализировать взаимосвязь нескольких результирующих показателей и большого числа переменных определяющих эти показатели.

В каноническом анализе

p  g ,

где p количество результативных показателей;

g количество переменных показателей.

Каноническая корреляция это корреляция между новыми каноническими переменными U и V:

U=a₁x₁+ a₂x₂ +…+ a_gx_g

V=b₁y₁+ b₂y₂ +…+ b_py_p

По аналогии с парной корреляцией теснота связи между каноническими переменными определяется каноническим коэффициентом корреляции r:

Проверка значимости полученных коэффициентов канонической корреляции: критерий Бартлетта.

Экономическая интериретация результатов канонического анализа.

Например, максимальный коэффициент канонической корреляции r₁=0,7 достигается при условии (для условного примера):

U₁=0,113x₁+1,085x₂ +…+ 0,8334x₃

V₁= 1,147y₁+0,841y₂

Т.к. r₁ близка к 1, значит связь между полученными линейными комбинациями исходных переменных тесная.

См.: 1. Ким Дж.-О., Мьюллер У.У. и др. Факторный, дискриминантный и кластерный анализ. Пер. с англ. М.: Финансы и статистика, 1989. - 215 с.

2. Ферестер Э., Ренц Б. Методы корреляционного и регрессионного анализа. - М.: Финансы и статистика, 1988. - 302 с.

Характеристика Компьютерных программ

VII. Компьютерный анализ многомерных статистических данных.

Кулаичев А.П. Методы и средства анализа данных в среде Windows Studio 6.0. М.: Информатика и компьютеры, 1996. - 257 с.
Петрович М.Л., Давидович М.В. Статистическое оценивание и проверка гипотез на ЭВМ. М.: Финансы и статистика, 1989. - 190 с.
Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере/ Под. ред. В.Э. Фигурнова. М.: ИНФРА М.: Финансы и статистика, 1997. - 528 с.
Статистические пакеты: SPSS, SAS, STATGRAPHICS (STATGRAPHICS FOR DOS, STATGRAPHICS FOR WINDOWS, DSTAT)
Версии STATGRAPHICS (Statistical Graphics System):

STATGRAPHICS for Windows (Версия 1.0);
STATGRAPHICS for DOS (Версия 3.1, версия 7.0);
STATGRAPHICS plus for Windows (Версия 1.0);
другие.

Пакет прикладных статистических программ DSTAT (см.: Автоматизированное рабочее место для статистической обработки данных. Шураков В.В., Дагитбеков Д.М., Мизрохи С.В., Ясеновский С.В. М.: Финансы и статистика, 1990. - 190 с.

Реализация методов многомерного статистического анализа на ЭВМ

Регрессионный анализ.

Пакет STATGRAPHICS

Простая регрессия (simple regression)
Интерактивное отбрасывание (interactive outliner rejection)
Множественная регрессия (multiple regression)
Пошаговая регрессия (stepwise regression)
Гребневая регрессия (ridge regression)
Нелинейная регрессия (nonlinear regression)

Коэффициент Дарбина-Уотсона, расчетные значения t-критерия для коэффициентов регрессии, множественный коэффициент детерминации, множественный коэффициент корреляции (см. Model fitting results for: в пакете). В разделе Regression Analysis имеется программа, позволяющая рассчитывать модели нелинейной регрессии:

Процедуры получения оценок параметров нелинейного уравнения регрессии см.: Афифи А., Эйзен С. Статистический анализ: подход с использованием ЭВМ. М.: Мир, 1982. - 448 с.

Пакет DSTAT

Множественная регрессия в разделе Статистик эксперт.

Факторный анализ.

Пакет STATGRAPHICS

Программа Principal components (главные компоненты) входит в раздел Многомерные методы (multivariate methods) и предназначена для расчета главных компонент.

Программа Факторный анализ (Factor analysis) в разделе Multivariate methods

Аналитические возможности программы расширяются за счет графического представления результатов.

Пакет DSTAT

Методы факторного анализа реализуются двумя программами раздела Статистик эксперт:

компонентный анализ
факторный анализ

В результате компонентного анализа вычисляются:

дисперсии главных компонент;
доли дисперсии главных компонент;
накопленный процент дисперсии;
главные компоненты;
индивидуальные значения главных компонент.

Аналогично выполняется и программа Факторный анализ.

Кластерный анализ

Пакет STATGRAPHICS

Программа Cluster Analysis из раздела Многомерные методы (multivariate methods).

В пакете STATGRAPHICS реализованы следующие методы:

неиерархический метод (Seeded)
метод средней связи (Average)
центроидный метод (Centroid)
метод “дальнего соседа” (Furthest)
метод “ближайшего соседа” (Nearest)
метод медианной связи (Median)

Пакет DSTAT

Кластерный анализ представлен только одним методом иерархическим агломеративным кластерным анализом.

В ходе работы алгоритма пользователь получает информацию о числе существующих кластеров, их составе и запрос о продолжении процедуры классификации. На экран выводится дендрограмма (при n  20).

Канонические корреляции

Пакет STATGRAPHICS

Метод реализуется при помощи программы Canonical Correlation (канонические корреляции) раздела Multivariate methods (многомерные методы).

Пакет DSTAT

Канонический корреляционный анализ в разделе Статистик эксперт.

Blog