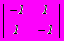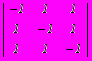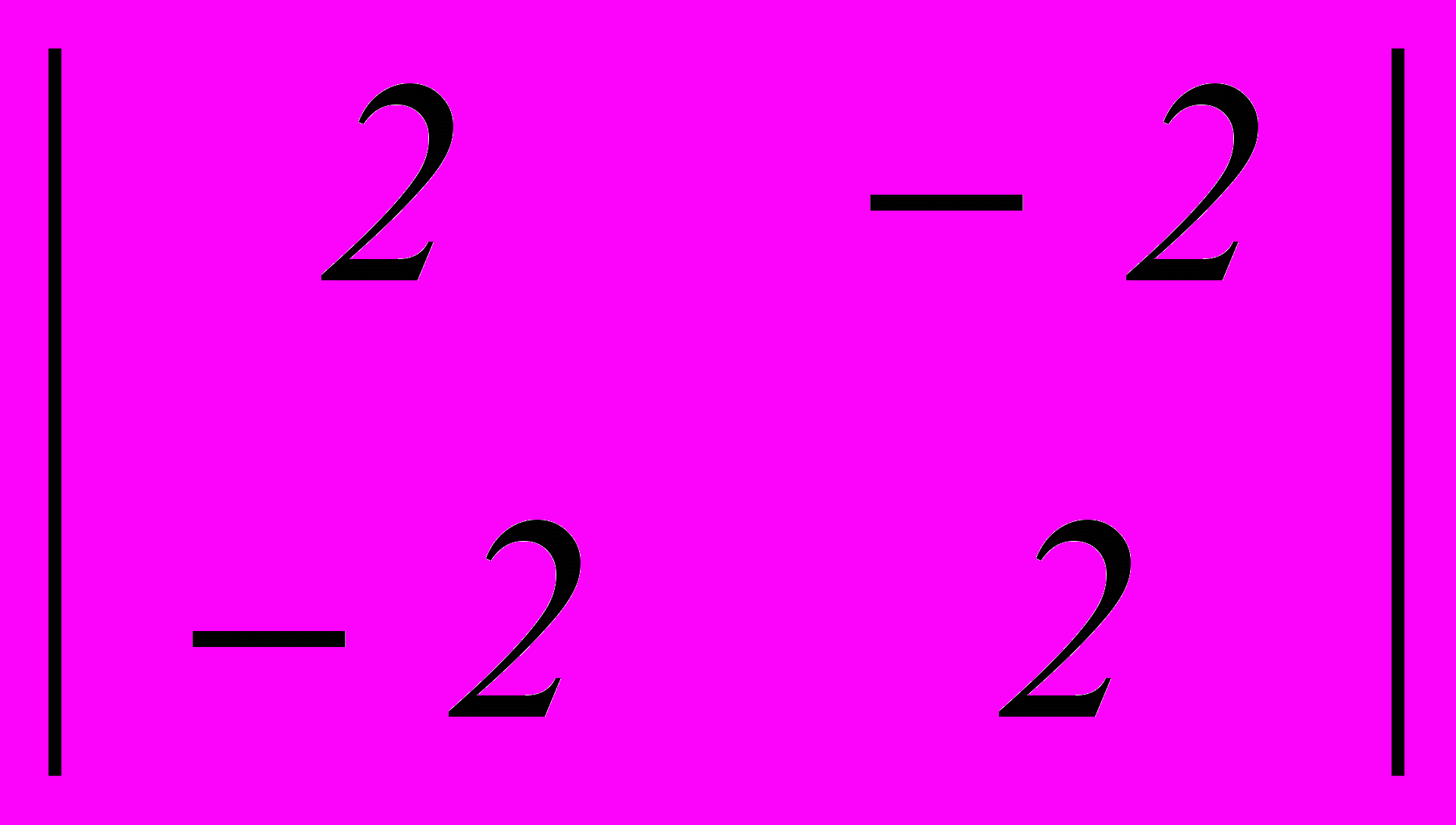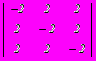Учебно-методический комплекс учебной дисциплины Математическое моделирование 032100. 00 Математика с дополнительной специальностью

Вид материала

Учебно-методический комплекс

Подобный материал:

• Учебно-методический комплекс учебной дисциплины дпп. Р. 01. Математическое конструирование, 83.94kb.
• Учебно-методический комплекс учебной дисциплины Геометрия Специальность 032100., 183.68kb.
• Программа дисциплины опд. Ф. 04. 1 «Теория и методика обучения математике» Специальность, 184.43kb.
• Программа дисциплины фтд. 00 «избранные главы алгебры» Специальность 032100. 01 Математика, 95.5kb.
• Учебно-методический комплекс учебной дисциплины ен. Ф. 01 Математика (аналитическая, 542.76kb.
• Учебно-методический комплекс дисциплины для преподавателей по специальности История, 2951.19kb.
• Учебно-методический комплекс учебной дисциплины Геометрические построения Специальность, 185.36kb.
• Рабочая программа учебной дисциплины дпп. Ф. 07. Теория чисел ооп, 386.12kb.
• Учебно-методический комплекс учебной дисциплины «численные методы и математическое, 428.92kb.
• Рабочая программа учебной дисциплины дпп. Ф. 08 Числовые системы ооп, 599.58kb.

Одноканальная СМО с отказами представляет собой телефонную линию. Заявка – вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов  = 0,5 вызовов в минуту. Средняя продолжительность разговора 1,5 мин. Все потоки событий – простейшие. Предельные (при t  .) параметры системы, q, A, Pотк, будут равны

1. q = 0,2; A = 0,6; Pотк = 0,8
   
2. q = 0,35; A = 0,4; Pотк = 0,65
   
3. q = 0,25; A = 0,5; Pотк = 0,75
   
4. q = 0,2; A = 0,4; Pотк = 0,8
   
5. q = 0,57; A = 0,29; Pотк = 0,43
   

На рисунке представлены 20 возможных стратегий выполнения проекта в координатах W – вероятность успешного завершения проекта, S – стоимость стратегии. Найдите множество вариантов, которые нельзя улушить (уменьшить S и увеличить W) по обоим критериям сразу.

1. Х1, Х2, Х3,Х4,Х5
   
2. Х12
   
3. Х16
   
4. Х20,Х19,Х17,Х16
   
5. Х17
   

Если один из игроков придерживается своей оптимальной смешанной стратегии, то

1. второй игрок может уменьшить проигрыш, если придерживается своей оптимальной стратегии
   
2. второй игрок выигрывает, применяя чистую стратегию
   
3. второй игрок может выиграть, применив маловероятный ход
   
4. для другого игрока невыгодно отклоняться от оптимальной стратегии
   
5. применив смешанную стратегию, второй игрок выигрывает
   

Чтобы свести задачу ЛП с ограничениями в виде неравенств к ОЗЛП необходимо

1. включить добавочные переменные в ограничения и целевую функцию
   
2. включить добавочные переменные в целевую функцию
   
3. включить добавочные переменные в ограничения
   
4. изменить целевую функцию
   

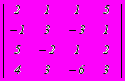Дана платежная матрица . Верхняя и нижняя цена игры составляет

1. –1, –1
   
2. 1, 1
   
3. 5, 3
   
4. 5, –3
   
5. 4, 5
   

Модель является детерминированной, если

1. известны пределы изменения всех элементов решения
   
2. фиксированы все внешние факторы—условия и пределы изменения факторов элементов решения
   
3. известны значения всех внешних факторов
   
4. заданы пределы изменения элементов решения, входящих в критерий эффективности
   
5. она не содержит неопределенных факторов
   

Локально-оптимальное решение – это

1. приближенное решение
   
2. оптимальное решение для конкретных значений неизвестных параметров
   
3. оптимальное решение в заданном диапазоне известных параметров
   
4. оптимальное «в среднем» решение
   

решение, полученное заменой случайных факторов на их математические ожидания Недостатком линейного составного критерия является

1. отсутствие объективных оценок весовых коэффициентов
   
2. частные показатели могут быть несоизмеримы
   
3. сложность использования методов численной оптимизации
   
4. частные показатели могут обращаться в нуль
   

Если один из игроков придерживается своей оптимальной смешанной стратегии, то

1. второй игрок выигрывает, применяя чистую стратегию
   
2. применив смешанную стратегию, второй игрок выигрывает
   
3. второй игрок может выиграть, применив маловероятный ход
   
4. для другого игрока невыгодно отклоняться от оптимальной стратегии
   
5. второй игрок может уменьшить проигрыш, если придерживается своей оптимальной стратегии
   

Седловых точек в игре может быть

1. только одна
   
2. несколько, если цена игры в каждой из них различна
   
3. несколько, причем цена игры в каждой из них одинакова
   
4. только две, для каждой из сторон своя
   

Метод оптимизации в среднем можно использовать если объект реализует свои функции многократно и относительно случайных факторов известно

1. математическое ожидание
   
2. совместное распределение
   
3. дисперсия
   
4. диапазон изменения
   
5. данные измерений
   

Критические работы необходимо выполнять

1. после выполнения всех работ с меньшими номерами
   
2. в последнюю очередь
   
3. в первую очередь
   
4. с учетом резервов времени
   
5. строго по графику (без задержки и сдвигов)
   

Ориентированный граф состояний системы отображает

1. узлы – состояния системы, дуги – возможные переходы из состояния в состояние
   
2. дуги – состояния системы, узлы — события перехода из состояния в состояние
   
3. структуру системы
   
4. связи между параметрами системы
   
5. связи между событиями в системе
   

Критический путь – это путь

1. состоящий из «фиктивных» работ
   
2. все работы которого не имеют резерва времени
   
3. на котором лежит максимальное количество работ
   
4. на котором лежит самая «длинная» работа
   
5. приводящий из точки А в А
   

Стратегией называется

1. совокупность правил игры
   
2. метод поиска оптимального хода
   
3. список возможных ходов
   
4. правило выбора личного хода
   
5. математическое описание игры
   

Постановка задачи ЛП о перевозках выполнена при условии

1. минимизации затрат на перевозки
   
2. максимальной прибыли
   
3. максимальное удовлетворение заявок
   
4. максимальное освобождение складов
   
5. кратчайшие пути перевозок
   

Каждый из двух игроков A и B одновременно и независимо друг от друга записывает на бумаге любое целое число. Если сумма чисел четная, то игрок A получает от игрока B 2 руб., если нечетная — платит игроку B 2 руб. Платежная матрица этой игры имеет вид:

1. 
   
2. 
   
3. 
   
4. 
   
5. 
   

Постановка задачи ЛП о загрузке станков выполнена при условии

1. полной загрузки станков
   
2. равномерной загрузке
   
3. минимальных убытках
   
4. максимальной прибыли
   

Два игрока A и B не глядя друг на друга, одновременно кладут на стол по картонному кружку с цифрами 1, 2, 3 или 4. После этого игроки расплачиваются друг с другом следующим образом: выигрыш равен сумме цифр, если она четная, то выигрыш получает игрок A иначе — игрок B. Стратегия игрока A всегда приводящая к выигрышу

1. не существует
   
2. существует если всегда показывать кружок 4
   
3. существует если всегда показывать кружок 2
   
4. существует если всегда показывать кружок 1
   
5. существует если всегда показывать кружок 3
   

Модель является детерминированной, если

1. заданы пределы изменения элементов решения, входящих в критерий эффективности
   
2. она не содержит неопределенных факторов
   
3. фиксированы все внешние факторы—условия и пределы изменения факторов элементов решения
   
4. известны пределы изменения всех элементов решения
   
5. известны значения всех внешних факторов
   

Условно-оптимальное управление – это управление, приводящее процесс

1. на шаг вперед
   
2. на шаг назад
   
3. из начальной точки в данную
   
4. из начальной точки в конечную
   
5. из данной точки в конечную
   

Функция условного оптимального выигрыша определяется

1. функциональным уравнением динамического программирования
   
2. функцией выигрыша на предыдущем шаге
   
3. суммой выигрышей на всех шагах процесса
   
4. функцией выигрыша на данном шаге
   
5. суммой выигрышей от данного шага до конца процесса
   

Число критических путей на сетевом графике

1. 3
   
2. 1
   
3. 1
   
4. равно (n + 1 – m), где n – число дуг, m – число узлов
   
5. равно числу работ деленному на число «фиктивных» работ
   

Постановка задачи ЛП о пищевом рационе выполнена при условии

1. заданной диеты
   
2. сбалансированности питания
   
3. необходимого количества продуктов
   
4. минимизации стоимости рациона
   
5. необходимой пищевой ценности
   

Недостатком составного критерия в виде дроби является

1. сложность использования методов численной оптимизации
   
2. возможность взаимной компенсации разнородных показателей
   
3. показатели стоящие в знаменателе могут обращаться в нуль
   
4. отсутствие объективных оценок весовых коэффициентов
   

Личным ходом называется выбор варианта действий

1. путем бросанием монеты или костей
   
2. скрытно от противника
   
3. игроком
   
4. направленных на введение противника в заблуждение
   
5. наносящий максимальный ущерб противнику
   

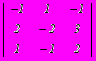Дана платежная матрица: . Верхняя и нижняя цена игры составляет

1. –1,–1
   
2. 1, –1
   
3. 3, –2
   
4. –2, –2
   
5. –1, 1
   

Метод динамического программирования заключается в

1. последовательной пошаговой оптимизации процесса
   
2. построении всех возможных решений с целью оптимизации
   
3. сведении нелинейных задач к линейным
   
4. преобразовании непрерывных процессов в дискретные
   
5. разделении процесса на этапы (шаги) и оптимизации каждого шага
   

Формулы Эрланга выражают

1. зависимость  от  и n
   
2. относительную пропускную способность
   
3. абсолютную пропускную способность
   
4. зависимость  от  и n
   
5. финальные вероятности всех состояний в зависимости от ,  и n
   

В игре с нулевой суммой

1. выигрыш одного игрока равен проигрышу другого
   
2. ведется игра на деньги
   
3. ведется игра на интерес
   
4. результат не выражается числом
   
5. ни один противник не может выиграть
   

Число этапов поиска оптимального управления по методу динамического программирования

1. 3
   
2. равно числу шагов
   
3. 2
   
4. 4
   
5. 1
   

Первый этап метода динамического программирования предусматривает

1. оптимизацию функции выигрыша на каждом шаге
   
2. пошаговую безусловную оптимизацию функции выигрыша
   
3. совместную оптимизацию функций выигрыша всех шагов
   
4. пошаговую оптимизацию функции условного оптимального выигрыша
   
5. пошаговую условную оптимизацию функции выигрыша
   

Транспортная задача с критерием времени классифицируется следующим образом

1. не является задачей ЛП и не решается методами ЛП
   
2. является задачей ЛП
   
3. не является задачей ЛП, но может быть к ней сведена
   
4. сводится к задаче ЛП путем введения «добавочных переменных»
   
5. может быть сведена к нескольким задачам ЛП
   

Элементами платежной матрицы парной игры являются значения

1. выигрышей обоих игроков для каждой пары стратегий
   
2. выигрышей одного из игроков для каждой пары стратегий обоих
   
3. выигрышей игрока для каждой его стратегии
   
4. разности выигрышей противников для каждой пары стратегий
   
5. выигрышей игрока для каждой стратегии противника
   

Условно-оптимальное управление оптимизирует функцию

1. сумму всех пошаговых выигрышей
   
2. выигрыша на данном шаге
   
3. условного оптимального выигрыша
   
4. сумму выигрышей на данном и всех предыдущих шагах
   
5. сумму выигрышей на данном и всех последующих шагах
   

Непрерывной цепью Маркова называется Марковский процесс, в котором

1. переход из состояния в состояние происходит в случайные моменты времени
   
2. известно распределение времени перехода из состояние в состояние
   
3. события перехода из состояния в состояние образуют полную группу
   
4. события перехода из состояния в состояние образуют неполную группу
   

Процесс называется марковским, если

1. переход системы из состояния в состояние подчиняется нормальному закону распределения
   
2. для каждого момента времени вероятность любого состояния системы в будущем зависит только от текущего состояния
   
3. система может вернуться в предыдущее состояние
   
4. система может переходить только в состояния с большими номерами
   

Изоморфизм – это

1. сохранение точных соотношений или взаимодействий между элементами
   
2. сходство по форме при различии основных структур
   
3. идентичность структуры
   
4. сходство по форме
   
5. взаимно-однозначное соответствие между элементами модели и объекта
   

Промежутки времени между моментами перехода непрерывной цепи Маркова из состояния в состояние распределены по

1. экспоненциальному закону
   
2. равномерному закону
   
3. нормальному закону
   
4. биномиальному закону
   

Одноканальная СМО с отказами представляет собой телефонную линию. Заявка – вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов  = 2 вызовов в минуту. Средняя продолжительность разговора 1,5 мин. Все потоки событий – простейшие. Предельные (при t  .) параметры системы, q, A, Pотк, будут равны

1. q = 0,3; A = 0,4; Pотк = 0,7
   
2. q = 0,25; A = 0,2; Pотк = 0,75
   
3. q = 0,15; A = 0,4; Pотк = 0,85
   
4. q = 0,25; A = 0,5; Pотк = 0,75
   
5. q = 0,2; A = 0,6; Pотк = 0,8
   

Теория игр позволяет

1. найти оптимальное решение в условиях неопределенности
   
2. дать рекомендации по рациональному образу действий в конфликтной ситуации
   
3. оптимизировать нелинейный критерий
   
4. заменить статистическую модель аналитической
   
5. оптимизировать задачу с нелинейными ограничениями
   

Постановка задачи ЛП о производстве сложного оборудования выполнена при условии:

1. минимизации затрат
   
2. достижения наиболее равномерной загрузки предприятий
   
3. максимизации загрузки предприятий
   
4. максимизации прибыли
   
5. максимизации числа полных комплектов оборудования
   

Для упрощения решения транспортной задачи с избытком запасов (неправильным балансом) необходимо

1. ввести фиктивные пункты назначения и отгрузки
   
2. изменить знак значений запасов
   
3. ввести фиктивный пункт назначения
   
4. ввести фиктивный пункт отгрузки