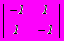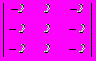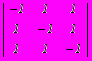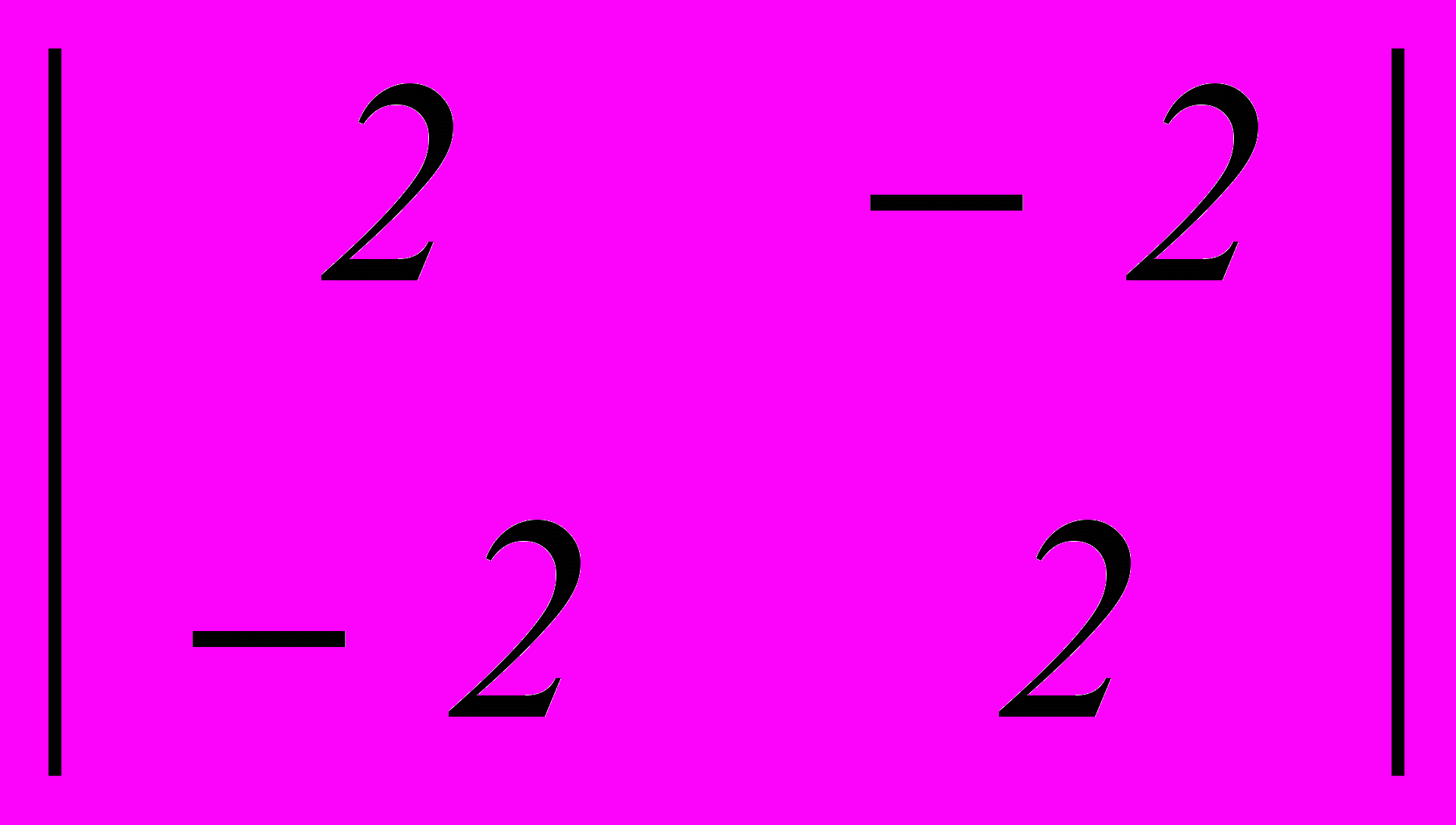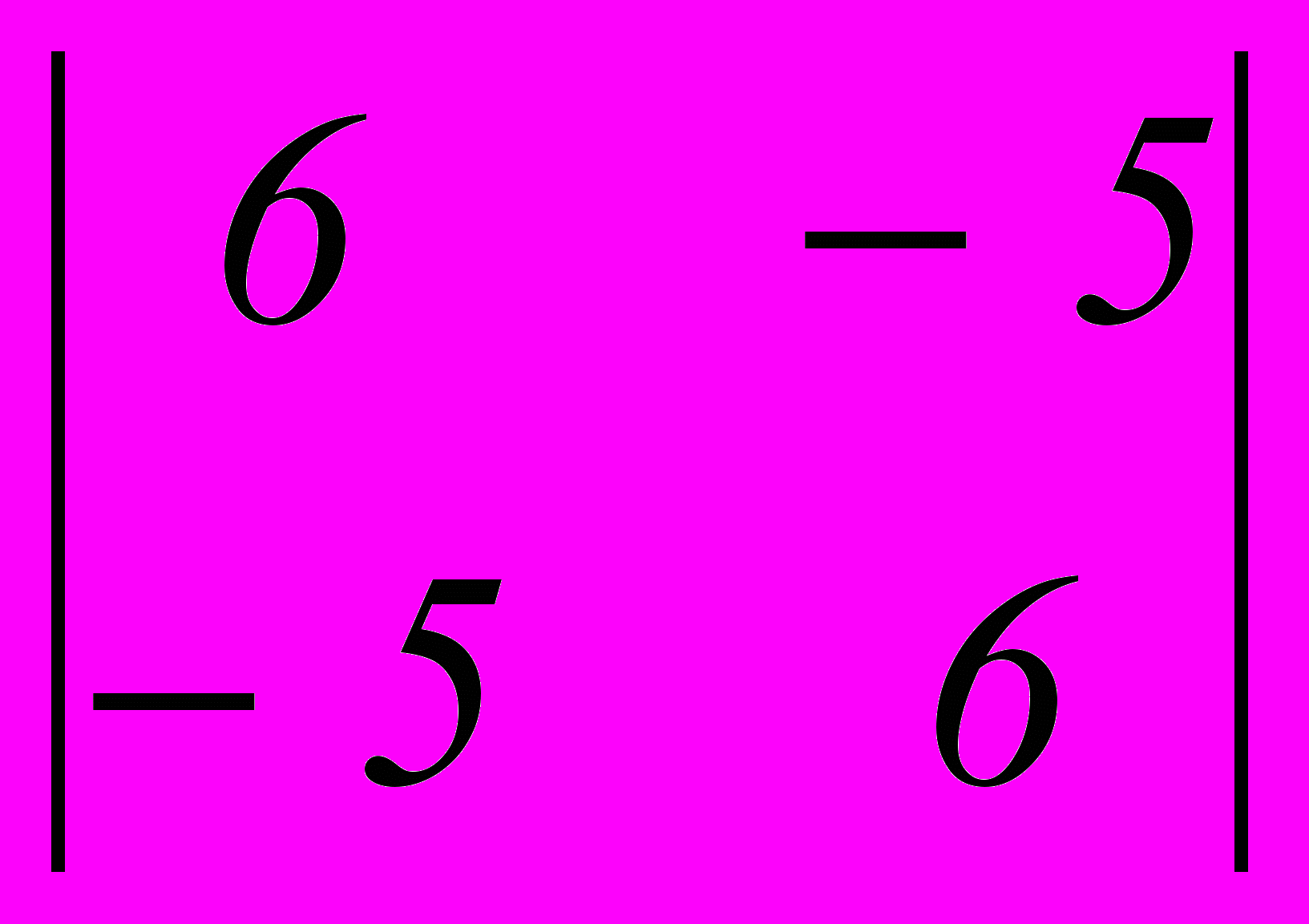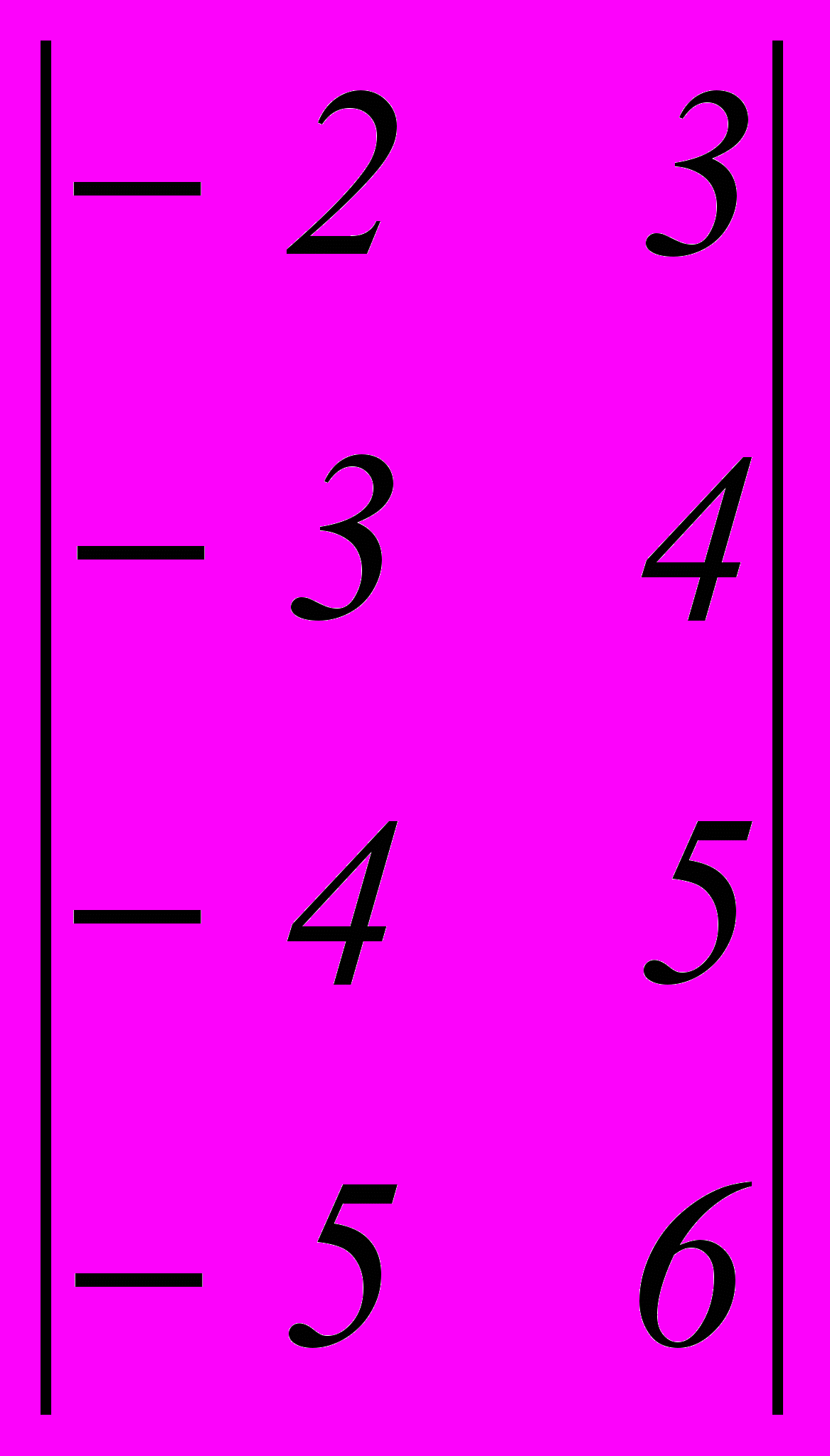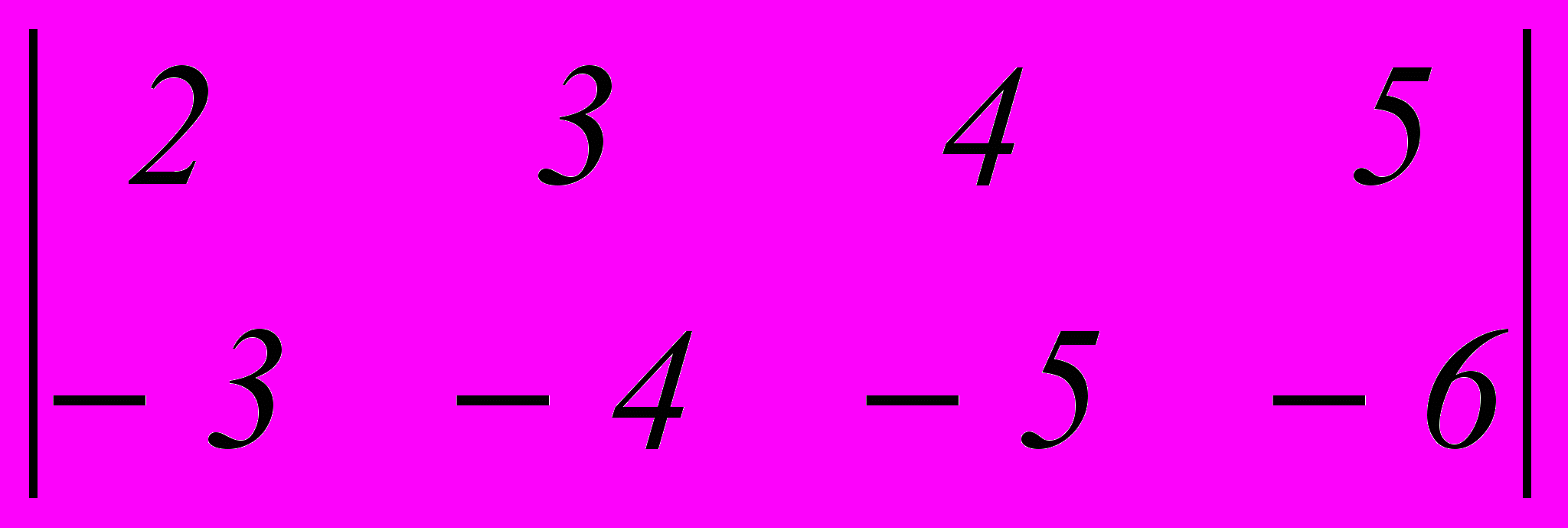Geum.ru

Учебно-методический комплекс учебной дисциплины Математическое моделирование 032100. 00 Математика с дополнительной специальностью

Вид материалаУчебно-методический комплекс
Подобный материал:
1   2   3   4

Дополнительная

    1. Бережная Е.В. Математические методы моделирования экономических систем.- М.: Финансы и статистика, 2000.
  1. Ермаков С. М., Мелис В. Б. Математический эксперимент с моделями сложных стохастических систем. – СПб.: ГУ, 1993.
  2. Лабскер Л. Г., Бабенко Л. В. Теория массового обслуживания в экономической сфере. – М.: Банки и биржи, ЮНИТИ, 1998.
  3. Литвинов В. В., Марьянович Т. П. Методы построения имитационных систем. – Киев: Наукова Думка, 1991.
  4. Мельник М. М. Экономико-математические методы и модели в планировании и управлении материально-техническим снабжением. – М.: Высшая школа, 1990.
  5. Перегудов Ф. И., Тарасенко Ф. П. Введение в системный анализ. – М.: Высшая школа, 1989.
  6. Проектирование и программная реализация экспертных систем на персональных ЭВМ/ Под ред. Д. Фахта. – М.: Финансы статистика, 1990.
  7. Советов Б. Я. Информационные технологии. – М.: Высшая школа, 1994.
  8. Чернов В. П., Ивановский В. Б. Теория массового обслуживания. – М.: ИНФРА-М, 2000.



Методические указания студентам по подготовке к практическим занятиям.


Контролирующие материалы для аттестации студентов по дисциплине.
  1. Случайные факторы модели приближенно можно заменить неслучайными когда
    1. распределение случайных факторов известно
    2. диапазон их разброса сравнительно мал
    3. невозможно определить характер их изменений
    4. известно их математическое ожидание
    5. объект реализует свою функцию многократно
  2. Метод оптимизации в среднем можно использовать если объект реализует свои функции многократно и относительно случайных факторов известно
    1. дисперсия
    2. математическое ожидание
    3. данные измерений
    4. совместное распределение
    5. диапазон изменения
  3. Игра называется парной тогда, когда
    1. все партнеры выступают как два противника
    2. партнеры имеют по две стратегии
    3. игра содержит только две стратегии
    4. все партнеры сгруппированы в пары
  4. Формулировка принципа оптимальности: Оптимальная стратегия обладает свойством оптимальности
    1. функции выигрыша на всех предыдущих шагах
    2. на предыдущих шагах процесса
    3. функции выигрыша на каждом шаге
    4. функции выигрыша на всех последующих шагах
    5. начиная с данного шага и до конца процесса
  5. Временной резерв это
    1. срок окончания самой «длинной» работы
    2. время, на которое может быть задержана работа без ущерба для общего срока
    3. сумма времени критических работ
    4. срок окончания последней работы
    5. срок окончания комплекса работ
  6. Нижней ценой игры называется
    1. максимальный выигрыш при наилучших (для него) действиях противника
    2. минимальный проигрыш при данной стратегии
    3. минимальная ставка хода
    4. минимальный выигрыш при данной стратегии
    5. минимальная ставка игры
  7. Ранг работы есть
    1. принадлежность работы к критическому пути
    2. максимальный ранг работ, на которые она опирается
    3. ее порядковый номер
    4. максимальный ранг работ, на которые она опирается плюс один
    5. максимальный ранг предшествующих работ минус один
  8. Чтобы свести задачу ЛП с ограничениями в виде неравенств к ОЗЛП необходимо
    1. включить добавочные переменные в ограничения и целевую функцию
    2. включить добавочные переменные в ограничения
    3. изменить целевую функцию
    4. включить добавочные переменные в целевую функцию
  9. Постановка задачи ЛП о пищевом рационе выполнена при условии
    1. необходимого количества продуктов
    2. сбалансированности питания
    3. минимизации стоимости рациона
    4. необходимой пищевой ценности
    5. заданной диеты
  10. Недостатком линейного составного критерия является
    1. частные показатели могут быть несоизмеримы
    2. отсутствие объективных оценок весовых коэффициентов
    3. частные показатели могут обращаться в нуль
    4. сложность использования методов численной оптимизации
  11. Верхней ценой игры называется
    1. минимальный проигрыш противника при наилучших (для нас) наших действиях
    2. максимальный проигрыш при данной стратегии
    3. максимальная ставка игры
    4. максимальная ставка хода
    5. максимальный выигрыш противника при наилучшей стратегии с нашей стороны
  12. Условно-оптимальное управление оптимизирует функцию
    1. выигрыша на данном шаге
    2. сумму всех пошаговых выигрышей
    3. условного оптимального выигрыша
    4. сумму выигрышей на данном и всех последующих шагах
    5. сумму выигрышей на данном и всех предыдущих шагах
  13. Время выполнения комплекса работ – это сумма времени
    1. критических работ
    2. работ, имеющих максимальную продолжительность
    3. «фиктивных» работ
    4. всех работ
  14. Дана платежная матрица 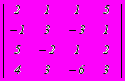. Верхняя и нижняя цена игры составляет
    1. 4, 5
    2. 5, 3
    3. –1, –1
    4. 5, –3
    5. 1, 1
  15. Критические работы необходимо выполнять
    1. в последнюю очередь
    2. в первую очередь
    3. после выполнения всех работ с меньшими номерами
    4. строго по графику (без задержки и сдвигов)
    5. с учетом резервов времени
  16. Ориентированный граф состояний системы отображает
    1. связи между параметрами системы
    2. узлы – состояния системы, дуги – возможные переходы из состояния в состояние
    3. структуру системы
    4. дуги – состояния системы, узлы — события перехода из состояния в состояние
    5. связи между событиями в системе
  17. По некоторой цели ведется стрельба. Состояния: 1 – цель не повреждена, 2 – цель повреждена, 3 – цель уничтожена. Компоненты вектора вероятностей упорядочены по номеру состояния В начальный момент состояние — 1. т.е. вектор вероятностей (1;0;0). Матрица переходных вероятностей состояния цели после выстрела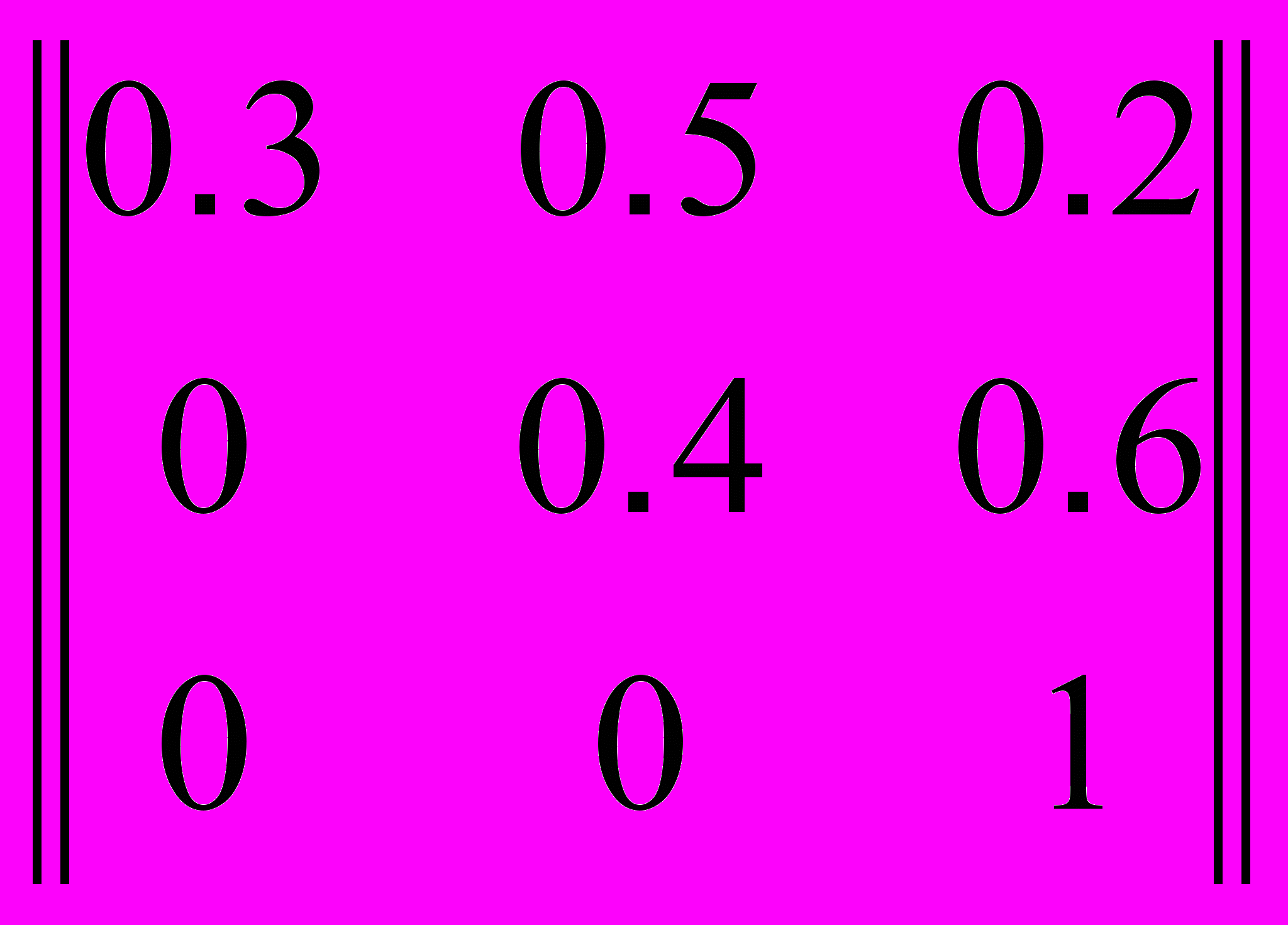. Вероятности состояний цели после двух выстрелов равны
    1. (0,02;0,06;0,129)
    2. (0,008; 0,163;0,129)
    3. (0,015;0,05;0,1)
    4. (0,108;0,07;0,029)
    5. (0,09; 0,35;0,56)
  18. Плотностью вероятностей перехода называется
    1. предел отношения
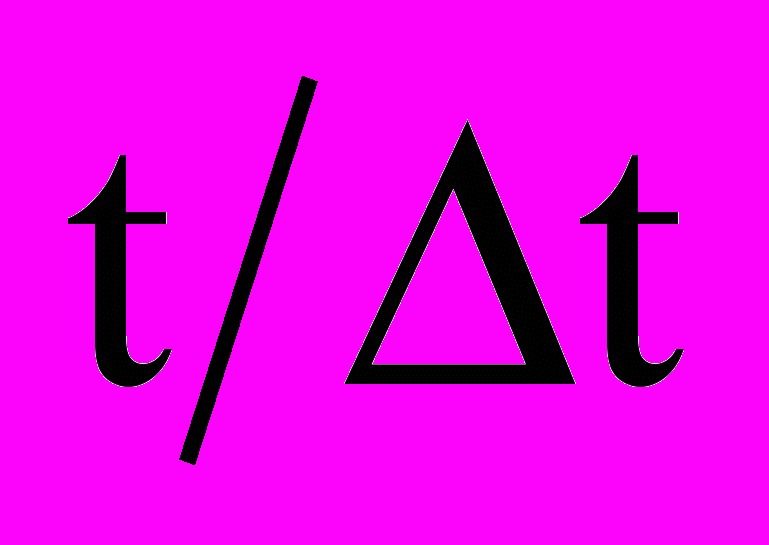
    2. вероятность переходов в зависимости от времени
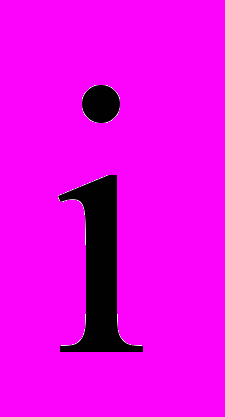    3. предел отношения вероятности перехода системы за время из состояния в состояние 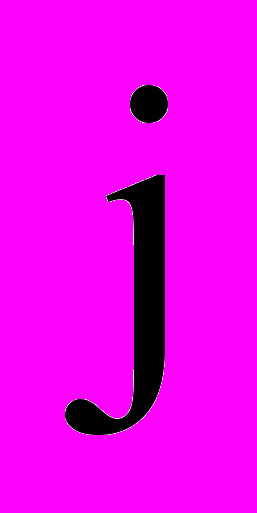к при
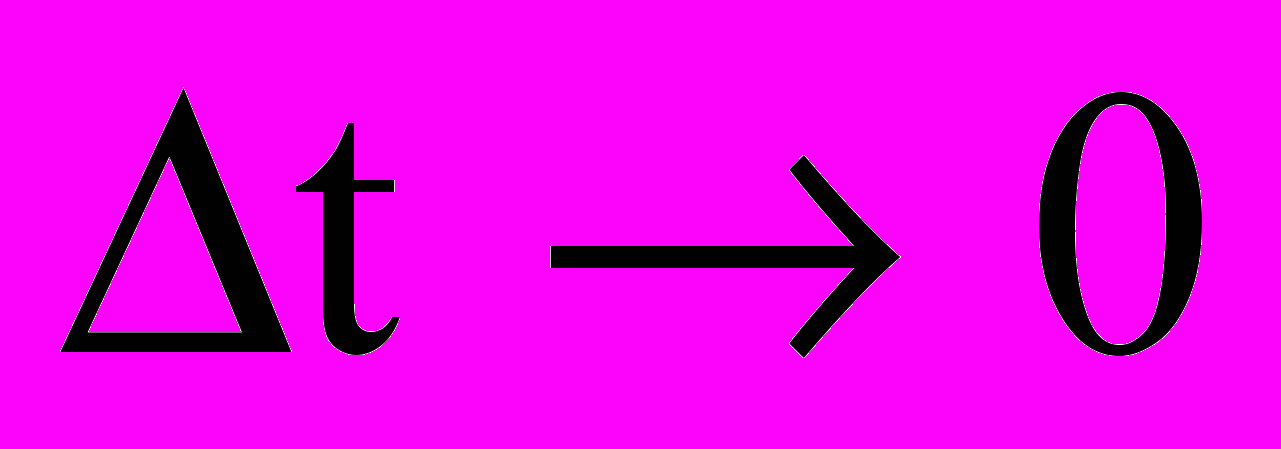
    4. непрерывная функция распределения
    5. дискретная функция распределения
  19. Каждый из двух игроков A и B одновременно и независимо друг от друга записывает на бумаге любое целое число. Если сумма чисел четная, то игрок A получает от игрока B 2 руб., если нечетная — платит игроку B 2 руб. Платежная матрица этой игры имеет вид:





  20. На рисунке представлены 20 возможных стратегий выполнения проекта в координатах W – вероятность успешного завершения проекта, S – стоимость стратегии. Найдите множество вариантов, которые нельзя улушить (уменьшить S и увеличить W) по обоим критериям сразу.

    1. Х1, Х2, Х3,Х4,Х5
    2. Х20,Х19,Х17,Х16
    3. Х16
    4. Х12
    5. Х17
  21. Основная теорема матричных игр (Дж.фон Неймана) утверждает, что
    1. не все игры конечны
    2. каждая конечная игра имеет одно решение
    3. каждая конечная игра имеет по крайней мере одно решение, возможно в области смешанных стратегий
    4. не все игры имеют решение
  22. Одноканальная СМО с отказами представляет собой телефонную линию. Заявка – вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов  = 2 вызовов в минуту. Средняя продолжительность разговора 1,5 мин. Все потоки событий – простейшие. Предельные (при t  .) параметры системы, q, A, Pотк, будут равны
    1. q = 0,25; A = 0,2; Pотк = 0,75
    2. q = 0,25; A = 0,5; Pотк = 0,75
    3. q = 0,15; A = 0,4; Pотк = 0,85
    4. q = 0,3; A = 0,4; Pотк = 0,7
    5. q = 0,2; A = 0,6; Pотк = 0,8
  23. Используя платежную матрицу 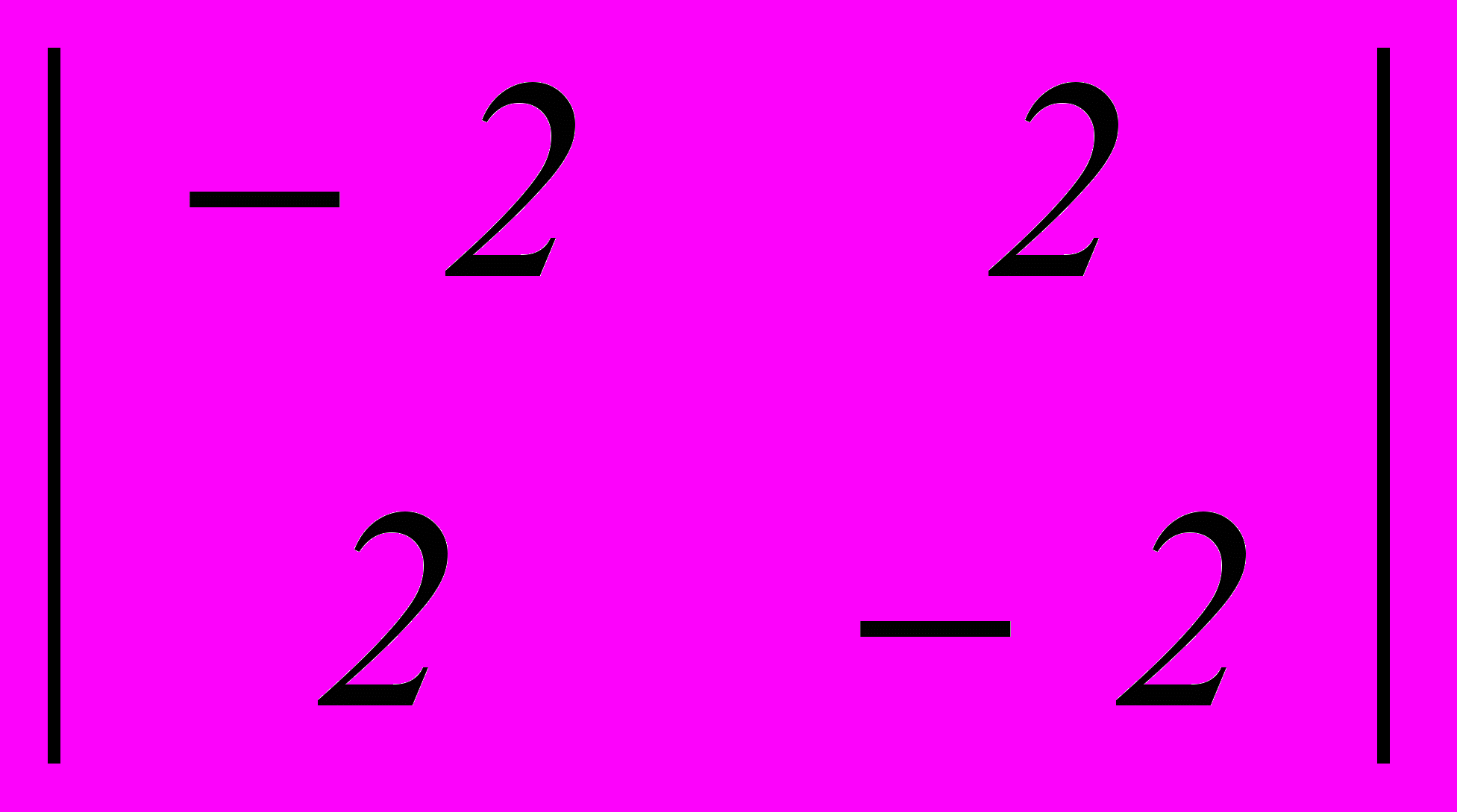, построить стратегию поведения игрока А, всегда приводящую к выигрышу
    1. нельзя
    2. можно, чередуя стратегии 1 и 2
    3. можно, всегда выбирая стратегию 2
    4. можно, всегда выбирая стратегию 1
    5. можно, используя механизм случайного выбора
  24. Два игрока A и B не глядя друг на друга, одновременно кладут на стол по картонному кружку с цифрами. Игрок A кладет кружки с цифрами 1, 2, 3 или 4. Игрок B — с цифрами 1 или 2. После этого игроки расплачиваются друг с другом следующим образом: выигрыш равен сумме цифр, если она четная, то выигрыш получает игрок A иначе — игрок B. Платежная матрица этой игры имеет вид:





  25. Транспортная задача с критерием времени классифицируется следующим образом
    1. является задачей ЛП
    2. не является задачей ЛП и не решается методами ЛП
    3. не является задачей ЛП, но может быть к ней сведена
    4. может быть сведена к нескольким задачам ЛП
    5. сводится к задаче ЛП путем введения «добавочных переменных»
  26. Непрерывной цепью Маркова называется Марковский процесс, в котором
    1. известно распределение времени перехода из состояние в состояние
    2. события перехода из состояния в состояние образуют неполную группу
    3. переход из состояния в состояние происходит в случайные моменты времени
    4. события перехода из состояния в состояние образуют полную группу
  27. Чистой ценой игры называют
    1. цену в седловой точке
    2. минимально-возможный выигрыш
    3. максимально-возможный проигрыш
    4. минимально-возможный проигрыш
    5. максимально-возможный выигрыш
  28. Для упрощения решения транспортной задачи с избытком заявок (неправильным балансом) необходимо
    1. ввести фиктивный пункт отгрузки
    2. ввести фиктивный пункт назначения
    3. изменить знак значений объемов поставок
    4. ввести фиктивные пункты назначения и отгрузки
  29. Одноканальная СМО с отказами представляет собой телефонную линию. Заявка – вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов  = 0,5 вызовов в минуту. Средняя продолжительность разговора 1,5 мин. Все потоки событий – простейшие. Предельные (при t  .) параметры системы, q, A, Pотк, будут равны
    1. q = 0,2; A = 0,4; Pотк = 0,8
    2. q = 0,57; A = 0,29; Pотк = 0,43
    3. q = 0,25; A = 0,5; Pотк = 0,75
    4. q = 0,35; A = 0,4; Pотк = 0,65
    5. q = 0,2; A = 0,6; Pотк = 0,8
  30. Временным сетевым графиком называется сетевой график,
    1. упорядоченный по времени выполнения работы
    2. на котором проставлена длительность работы
    3. на котором длина стрелки пропорциональна длительности работы
    4. построенный вдоль временной оси с учетом длительности работ
  31. Можно подсчитать вероятность существования органической жизни на Марсе.
    1. да, если имеются статистические данные
    2. на Марсе жизни нет
    3. нет
    4. да
    5. да, рассчитав коэффициенты подобия между экологическими параметрами Земли и Марса
  32. Число критических путей на сетевом графике
    1. 1
    2. равно числу работ деленному на число «фиктивных» работ
    3. равно (n + 1 – m), где n – число дуг, m – число узлов
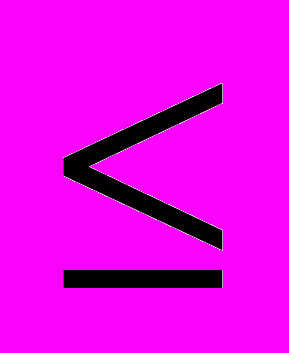    4. 3
    5. 1
  33. Дана платежная матрица: 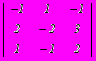. Верхняя и нижняя цена игры составляет
    1. –2, –2
    2. 3, –2
    3. 1, –1
    4. –1, 1
    5. –1,–1
  34. Формулы Эрланга выражают
    1. зависимость  от  и n
    2. абсолютную пропускную способность
    3. зависимость  от  и n
    4. относительную пропускную способность
    5. финальные вероятности всех состояний в зависимости от ,  и n
  35. Промежутки времени между моментами перехода непрерывной цепи Маркова из состояния в состояние распределены по
    1. нормальному закону
    2. экспоненциальному закону
    3. равномерному закону
    4. биномиальному закону
  36. Чтобы свести задачу ЛП «на минимум» к задаче «на максимум» необходимо
    1. взять дополнительную величину 1/L целевой функции
    2. поменять знаки bj на – bj
    3. поменять знаки aij на – aij
    4. поменять знак целевой функции
  37. взять обратную величину 1/L целевой функции По некоторой цели ведется стрельба. Состояния: 1 – цель не повреждена, 2 – цель повреждена, 3 – цель уничтожена. Компоненты вектора вероятностей упорядочены по номеру состояния В начальный момент состояние — 1. т.е. вектор вероятностей (1;0;0). Матрица переходных вероятностей состояния цели после выстрела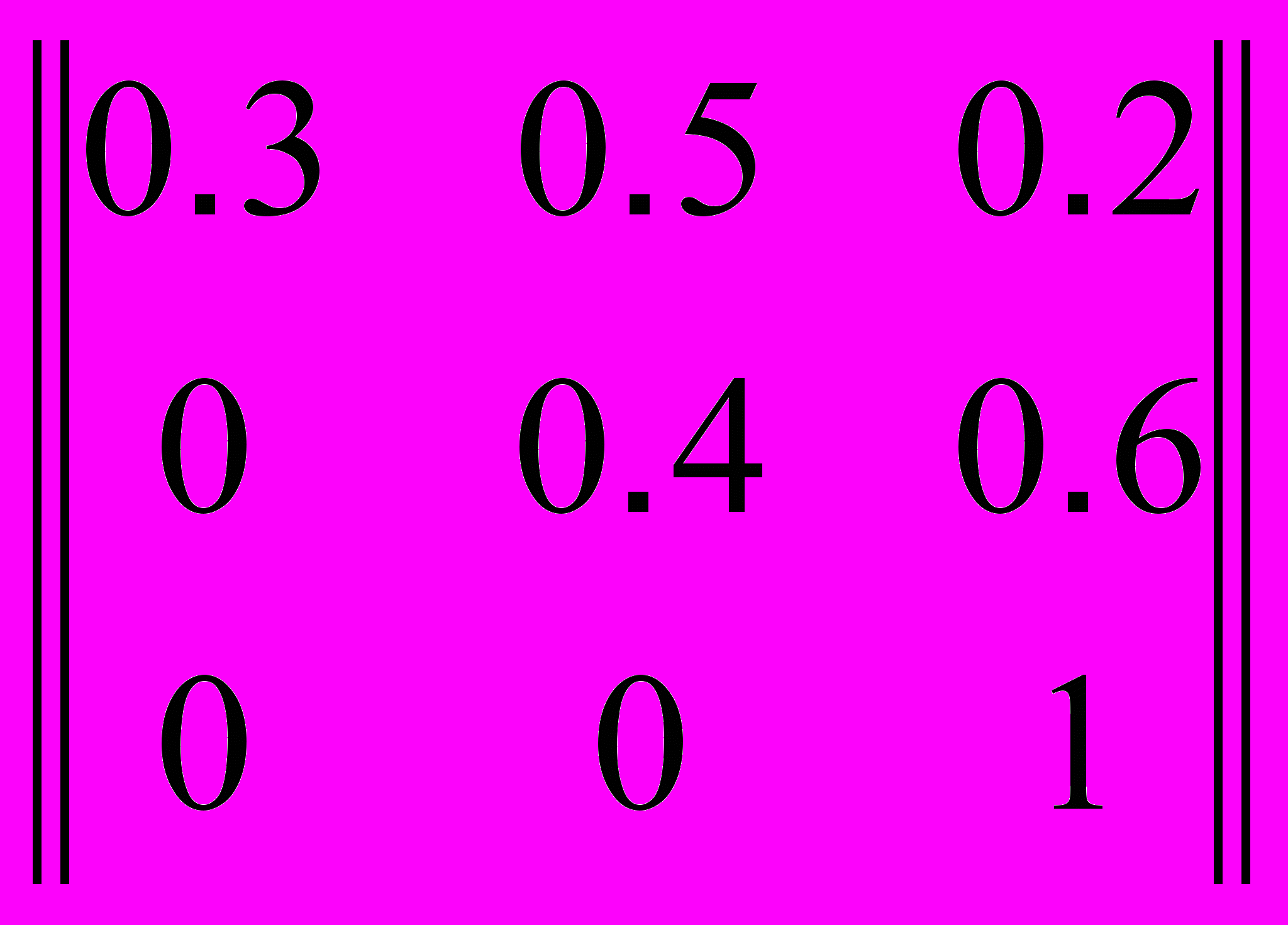. Вероятности состояний цели после двух выстрелов равны
    1. (0,008; 0,163;0,129)
    2. (0,108;0,07;0,029)
    3. (0,02;0,06;0,129)
    4. (0,015;0,05;0,1)
    5. (0,09; 0,35;0,56)
  38. Критические работы необходимо выполнять
    1. с учетом резервов времени
    2. строго по графику (без задержки и сдвигов)
    3. в последнюю очередь
    4. после выполнения всех работ с меньшими номерами
    5. в первую очередь
  39. Постановка задачи ЛП о пищевом рационе выполнена при условии
    1. минимизации стоимости рациона
    2. сбалансированности питания
    3. необходимого количества продуктов
    4. заданной диеты
    5. необходимой пищевой ценности
  40. На рисунке представлены 20 возможных стратегий выполнения проекта в координатах W – вероятность успешного завершения проекта, S – стоимость стратегии. Найдите множество вариантов, которые нельзя улушить (уменьшить S и увеличить W) по обоим критериям сразу.

    1. Х12
    2. Х1, Х2, Х3,Х4,Х5
    3. Х17
    4. Х16
    5. Х20,Х19,Х17,Х16
  41. В задаче о выборе решений в условиях неопределенности
    1. некоторые параметры объекта содержат элемент неопределенности
    2. не все параметры объекта являются управляемыми
    3. не все параметры объекта поддаются изменению
    4. не все параметры объекта и/или критерия эффективности известны заранее
  42. Стратегией называется
    1. метод поиска оптимального хода
    2. правило выбора личного хода
    3. математическое описание игры
    4. список возможных ходов
    5. совокупность правил игры
  43. Число этапов поиска оптимального управления по методу динамического программирования
    1. равно числу шагов
    2. 1
    3. 3
    4. 4
    5. 2
  44. Марковским процессом с дискретным временем называют процесс, в котором
    1. интервалы времени между сменой состояний системы дискретны
    2. переход из состояния в состояние возможен лишь в заранее фиксированные моменты времени
    3. можно пронумеровать все возможные состояния системы, а переход из состояния в состояние осуществляется скачком
    4. вероятность перехода из состояния в состояние описывается дискретной функцией распределения
    5. имеется конечный набор состояний
  45. Два игрока A и B не глядя друг на друга, одновременно кладут на стол по картонному кружку с цифрами 1, 2, 3 или 4. После этого игроки расплачиваются друг с другом следующим образом: выигрыш равен сумме цифр, если она четная, то выигрыш получает игрок A иначе — игрок B. Стратегия игрока A всегда приводящая к выигрышу
    1. существует если всегда показывать кружок 4
    2. существует если всегда показывать кружок 1
    3. не существует
    4. существует если всегда показывать кружок 2
    5. существует если всегда показывать кружок 3
  46. Решением уравнений Колмогорова является (являются)
    1. время завершения процесса
    2. вероятности состояний на конечном шаге
    3. вероятности перехода из состояния в состояние
    4. вероятности состояний в любой момент времени
    5. вероятности перехода в конечное состояние
  47. Одноканальная СМО с отказами представляет собой телефонную линию. Заявка – вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов  = 2 вызовов в минуту. Средняя продолжительность разговора 1,5 мин. Все потоки событий – простейшие. Предельные (при t  .) параметры системы, q, A, Pотк, будут равны
    1. q = 0,2; A = 0,6; Pотк = 0,8
    2. q = 0,25; A = 0,5; Pотк = 0,75
    3. q = 0,15; A = 0,4; Pотк = 0,85
    4. q = 0,3; A = 0,4; Pотк = 0,7
    5. q = 0,25; A = 0,2; Pотк = 0,75
  48. Временным сетевым графиком называется сетевой график,
    1. на котором длина стрелки пропорциональна длительности работы
    2. упорядоченный по времени выполнения работы
    3. построенный вдоль временной оси с учетом длительности работ
    4. на котором проставлена длительность работы
  49. Случайные факторы модели приближенно можно заменить неслучайными когда
    1. диапазон их разброса сравнительно мал
    2. известно их математическое ожидание
    3. объект реализует свою функцию многократно
    4. невозможно определить характер их изменений
    5. распределение случайных факторов известно