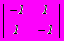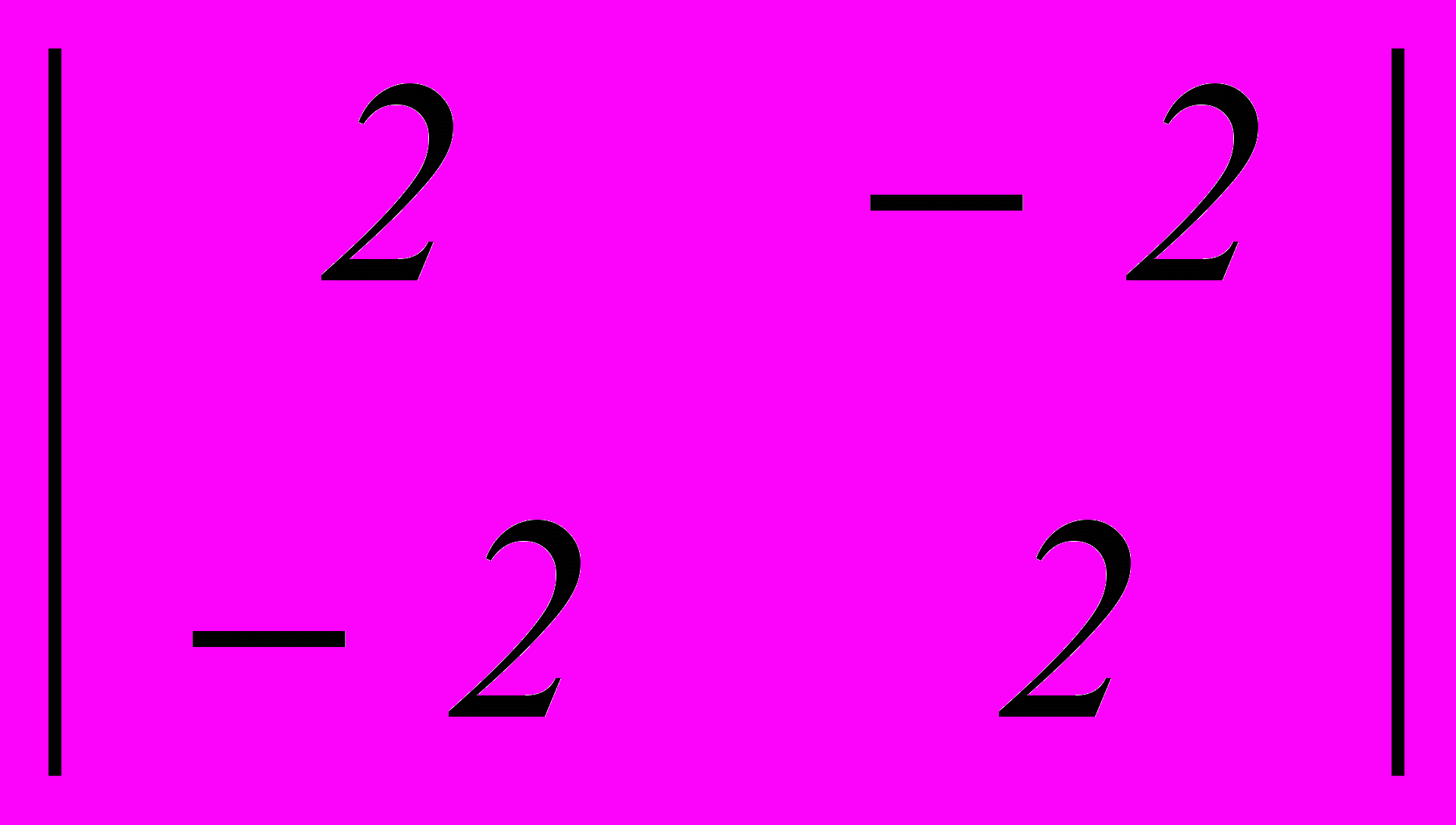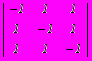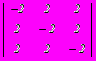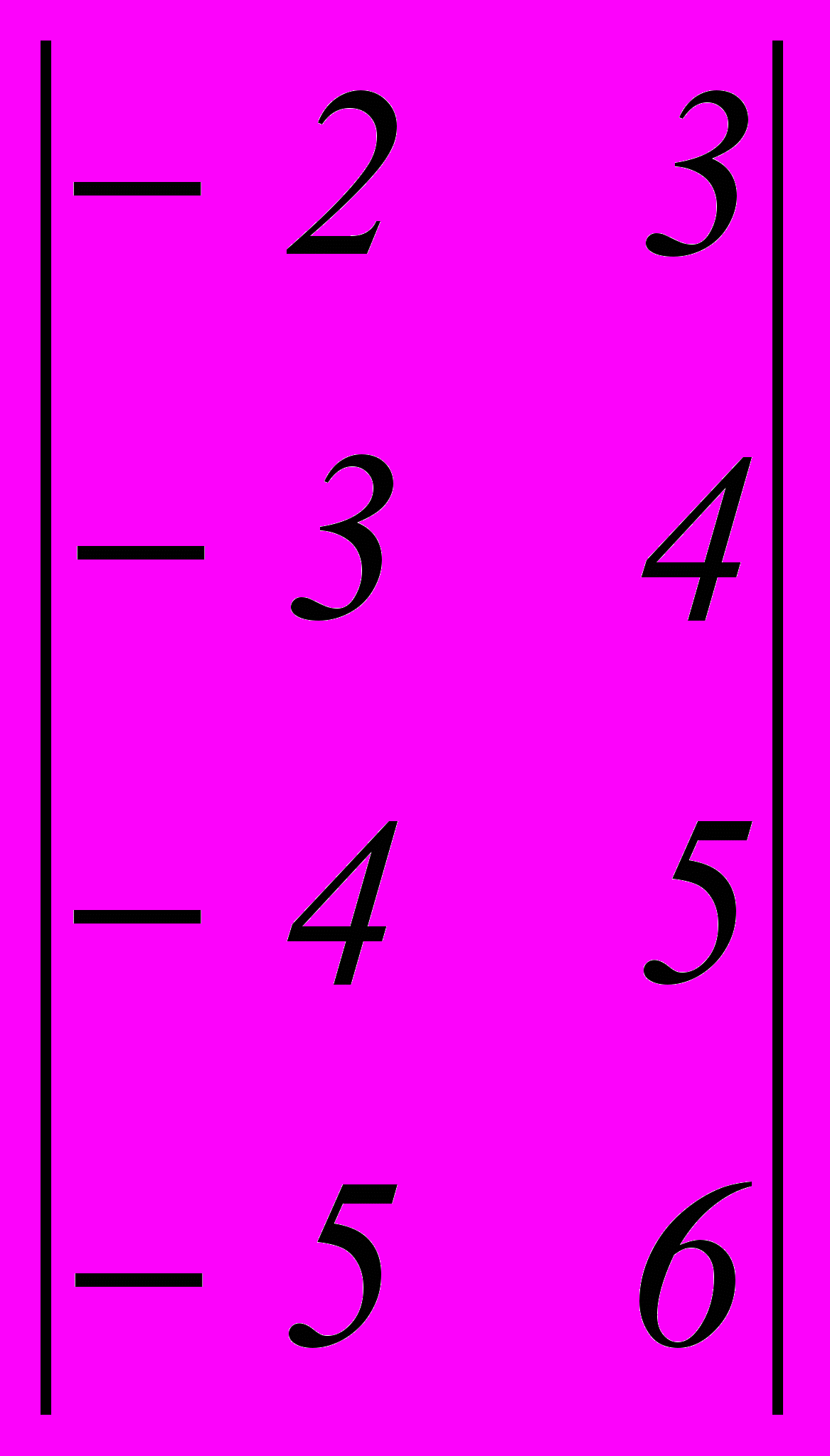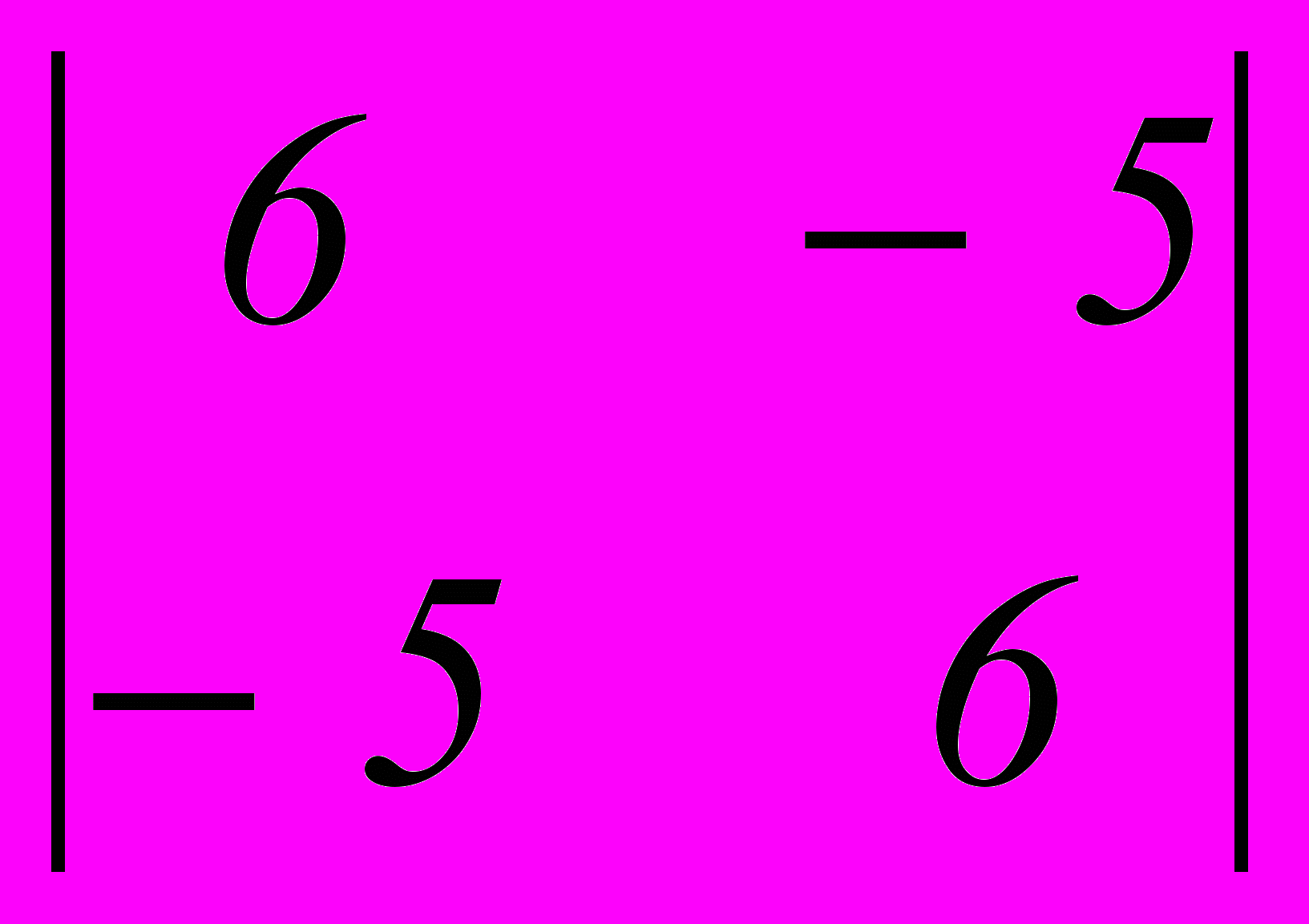Учебно-методический комплекс учебной дисциплины Математическое моделирование 032100. 00 Математика с дополнительной специальностью

Вид материала

Учебно-методический комплекс

Подобный материал:

• Учебно-методический комплекс учебной дисциплины дпп. Р. 01. Математическое конструирование, 83.94kb.
• Учебно-методический комплекс учебной дисциплины Геометрия Специальность 032100., 183.68kb.
• Программа дисциплины опд. Ф. 04. 1 «Теория и методика обучения математике» Специальность, 184.43kb.
• Программа дисциплины фтд. 00 «избранные главы алгебры» Специальность 032100. 01 Математика, 95.5kb.
• Учебно-методический комплекс учебной дисциплины ен. Ф. 01 Математика (аналитическая, 542.76kb.
• Учебно-методический комплекс дисциплины для преподавателей по специальности История, 2951.19kb.
• Учебно-методический комплекс учебной дисциплины Геометрические построения Специальность, 185.36kb.
• Рабочая программа учебной дисциплины дпп. Ф. 07. Теория чисел ооп, 386.12kb.
• Учебно-методический комплекс учебной дисциплины «численные методы и математическое, 428.92kb.
• Рабочая программа учебной дисциплины дпп. Ф. 08 Числовые системы ооп, 599.58kb.

Постановка задачи ЛП о распределении ресурсов выполнена при условии

1. минимальной себестоимости
   
2. минимальных (общих) затрат
   
3. использовании всех ресурсов
   
4. максимальной прибыли
   
5. максимальном удовлетворении спроса
   

Гомоморфизм – это

1. сходство по форме при различии основных структур
   
2. идентичность структуры
   
3. сохранение точных соотношений или взаимодействий между элементами
   
4. взаимно-однозначное соответствие между элементами модели и объекта
   

Число критических путей на сетевом графике

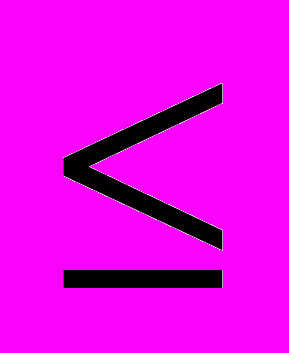1. 3
   
2. равно (n + 1 – m), где n – число дуг, m – число узлов
   
3. равно числу работ деленному на число «фиктивных» работ
   
4. 1
   
5. 1
   

Основная теорема матричных игр (Дж.фон Неймана) утверждает, что

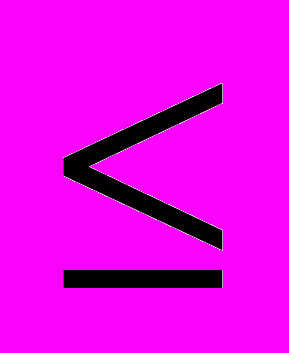1. каждая конечная игра имеет одно решение
   
2. каждая конечная игра имеет по крайней мере одно решение, возможно в области смешанных стратегий
   
3. не все игры имеют решение
   
4. не все игры конечны
   

Каждый из двух игроков A и B одновременно и независимо друг от друга записывает на бумаге любое целое число. Если сумма чисел четная, то игрок A получает от игрока B 2 руб., если нечетная — платит игроку B 2 руб. Платежная матрица этой игры имеет вид:

1. 
   
2. 
   
3. 
   
4. 
   
5. 
   

Относительная пропускная способность есть

1. номинальная производительность системы
   
2. математическое ожидание интенсивности обслуживания
   
3. максимальная производительность системы
   
4. среднее число заявок, которое может обслужить система в единицу времени
   
5. отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок
   

Элементами платежной матрицы парной игры являются значения

1. выигрышей одного из игроков для каждой пары стратегий обоих
   
2. разности выигрышей противников для каждой пары стратегий
   
3. выигрышей игрока для каждой стратегии противника
   
4. выигрышей игрока для каждой его стратегии
   
5. выигрышей обоих игроков для каждой пары стратегий
   

Два игрока A и B не глядя друг на друга, одновременно кладут на стол по картонному кружку с цифрами. Игрок A кладет кружки с цифрами 1, 2, 3 или 4. Игрок B — с цифрами 1 или 2. После этого игроки расплачиваются друг с другом следующим образом: выигрыш равен сумме цифр, если она четная, то выигрыш получает игрок A иначе — игрок B. Платежная матрица этой игры имеет вид:

1. 
   
2. 
   
3. 
   
4. 
   
5. 
   

Второй этап метода динамического программирования предусматривает безусловную оптимизацию

1. функций выигрыша в последовательности шагов, обратной первому этапу
   
2. совместную оптимизацию функций выигрыша всех шагов
   
3. функций условного оптимального выигрыша в последовательности шагов, обратной первому этапу
   
4. функций условного оптимального выигрыша в произвольной последовательности шагов
   
5. функций выигрыша в произвольной последовательности шагов
   

Математический анализ систем массового обслуживания облегчается если

1. процесс, протекающий в системе – марковский
   
2. процесс, протекающий в системе – непрерывный
   
3. процесс, протекающий в системе – дискретный
   
4. система имеет конечное число состояний
   

Изоморфизм – это

1. идентичность структуры
   
2. сходство по форме
   
3. взаимно-однозначное соответствие между элементами модели и объекта
   
4. сохранение точных соотношений или взаимодействий между элементами
   
5. сходство по форме при различии основных структур
   

Постановка задачи ЛП о перевозках выполнена при условии

1. кратчайшие пути перевозок
   
2. минимизации затрат на перевозки
   
3. максимальное освобождение складов
   
4. максимальной прибыли
   
5. максимальное удовлетворение заявок
   

Ранг работы есть

1. принадлежность работы к критическому пути
   
2. максимальный ранг работ, на которые она опирается
   
3. ее порядковый номер
   
4. максимальный ранг работ, на которые она опирается плюс один
   
5. максимальный ранг предшествующих работ минус один
   

Можно подсчитать вероятность существования органической жизни на Марсе.

1. на Марсе жизни нет
   
2. да
   
3. да, рассчитав коэффициенты подобия между экологическими параметрами Земли и Марса
   
4. да, если имеются статистические данные
   
5. нет
   

Метод оптимизации в среднем можно использовать если объект реализует свои функции многократно и относительно случайных факторов известно

1. диапазон изменения
   
2. математическое ожидание
   
3. данные измерений
   
4. совместное распределение
   
5. дисперсия
   

Абсолютная пропускная способность есть

1. математическое ожидание интенсивности обслуживания
   
2. максимальная производительность системы
   
3. отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок
   
4. номинальная производительность системы
   
5. среднее число заявок, которое может обслужить система в единицу времени
   

Формулировка принципа оптимальности: Оптимальная стратегия обладает свойством оптимальности

1. функции выигрыша на каждом шаге
   
2. функции выигрыша на всех последующих шагах
   
3. начиная с данного шага и до конца процесса
   
4. на предыдущих шагах процесса
   
5. функции выигрыша на всех предыдущих шагах
   

Одноканальная СМО с отказами представляет собой телефонную линию. Заявка – вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов  = 0,5 вызовов в минуту. Средняя продолжительность разговора 1,5 мин. Все потоки событий – простейшие. Предельные (при t  .) параметры системы, q, A, Pотк, будут равны

1. q = 0,57; A = 0,29; Pотк = 0,43
   
2. q = 0,2; A = 0,6; Pотк = 0,8
   
3. q = 0,2; A = 0,4; Pотк = 0,8
   
4. q = 0,35; A = 0,4; Pотк = 0,65
   
5. q = 0,25; A = 0,5; Pотк = 0,75
   

Для упрощения решения транспортной задачи с избытком заявок (неправильным балансом) необходимо

1. ввести фиктивный пункт назначения
   
2. изменить знак значений объемов поставок
   
3. ввести фиктивный пункт отгрузки
   
4. ввести фиктивные пункты назначения и отгрузки
   

Ориентированный граф состояний системы отображает

1. структуру системы
   
2. связи между параметрами системы
   
3. связи между событиями в системе
   
4. узлы – состояния системы, дуги – возможные переходы из состояния в состояние
   
5. дуги – состояния системы, узлы — события перехода из состояния в состояние
   

Недостатком линейного составного критерия является

1. сложность использования методов численной оптимизации
   
2. отсутствие объективных оценок весовых коэффициентов
   
3. частные показатели могут быть несоизмеримы
   
4. частные показатели могут обращаться в нуль
   

Личным ходом называется выбор варианта действий

1. скрытно от противника
   
2. направленных на введение противника в заблуждение
   
3. наносящий максимальный ущерб противнику
   
4. путем бросанием монеты или костей
   
5. игроком
   

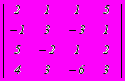Дана платежная матрица . Верхняя и нижняя цена игры составляет

1. 1, 1
   
2. 5, 3
   
3. –1, –1
   
4. 5, –3
   

4, 5 Личным ходом называется выбор варианта действий

1. направленных на введение противника в заблуждение
   
2. скрытно от противника
   
3. путем бросанием монеты или костей
   
4. наносящий максимальный ущерб противнику
   
5. игроком
   

Первый этап метода динамического программирования предусматривает

1. оптимизацию функции выигрыша на каждом шаге
   
2. пошаговую оптимизацию функции условного оптимального выигрыша
   
3. пошаговую условную оптимизацию функции выигрыша
   
4. совместную оптимизацию функций выигрыша всех шагов
   
5. пошаговую безусловную оптимизацию функции выигрыша
   

Изоморфизм – это

1. сходство по форме
   
2. сходство по форме при различии основных структур
   
3. идентичность структуры
   
4. взаимно-однозначное соответствие между элементами модели и объекта
   
5. сохранение точных соотношений или взаимодействий между элементами
   

Ориентированный граф состояний системы отображает

1. связи между параметрами системы
   
2. узлы – состояния системы, дуги – возможные переходы из состояния в состояние
   
3. дуги – состояния системы, узлы — события перехода из состояния в состояние
   
4. связи между событиями в системе
   
5. структуру системы
   

Два игрока A и B не глядя друг на друга, одновременно кладут на стол по картонному кружку с цифрами 1, 2, 3 или 4. После этого игроки расплачиваются друг с другом следующим образом: выигрыш равен сумме цифр, если она четная, то выигрыш получает игрок A иначе — игрок B. Стратегия игрока A всегда приводящая к выигрышу

1. существует если всегда показывать кружок 2
   
2. существует если всегда показывать кружок 4
   
3. не существует
   
4. существует если всегда показывать кружок 1
   
5. существует если всегда показывать кружок 3
   

В конце года завод находится в одном из двух состояний: 1 – спрос есть, 2 – спроса нет, в зависимости от наличия или отсутствия спроса на производимую продукцию. При наличии спроса он сохранится в течение следующего года с вероятностью 4/5. Если спроса нет, то принимаются меры по улучшению производства, в результате чего с вероятностью 3/5 завод к концу следующего года перейдет в состояние 1. Исходя из условий задачи матрицу переходных вероятностей можно представить как:

1. 
   
2. 
   
3. 
   
4. 
   
5. 
   

Число этапов поиска оптимального управления по методу динамического программирования

1. 2
   
2. 4
   
3. 3
   
4. равно числу шагов
   
5. 1
   

Седловая точка игры существует, если

1. верхняя цена больше нижней
   
2. верхняя цена игры равна 0
   
3. игра имеет нулевую сумму
   
4. верхняя цена меньше нижней
   
5. верхняя цена игры равна нижней
   

Промежутки времени между моментами перехода непрерывной цепи Маркова из состояния в состояние распределены по

1. нормальному закону
   
2. экспоненциальному закону
   
3. биномиальному закону
   
4. равномерному закону
   

Непрерывной цепью Маркова называется Марковский процесс, в котором

1. переход из состояния в состояние происходит в случайные моменты времени
   
2. события перехода из состояния в состояние образуют полную группу
   
3. известно распределение времени перехода из состояние в состояние
   
4. события перехода из состояния в состояние образуют неполную группу
   

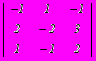Дана платежная матрица: . Верхняя и нижняя цена игры составляет

1. –2, –2
   
2. –1, 1
   
3. –1,–1
   
4. 1, –1
   
5. 3, –2
   

Теория игр позволяет

1. оптимизировать задачу с нелинейными ограничениями
   
2. дать рекомендации по рациональному образу действий в конфликтной ситуации
   
3. заменить статистическую модель аналитической
   
4. оптимизировать нелинейный критерий
   
5. найти оптимальное решение в условиях неопределенности
   

Для упрощения решения транспортной задачи с избытком заявок (неправильным балансом) необходимо

1. ввести фиктивные пункты назначения и отгрузки
   
2. изменить знак значений объемов поставок
   
3. ввести фиктивный пункт отгрузки
   
4. ввести фиктивный пункт назначения
   

Верхней ценой игры называется

1. максимальный выигрыш противника при наилучшей стратегии с нашей стороны
   
2. максимальный проигрыш при данной стратегии
   
3. максимальная ставка хода
   
4. минимальный проигрыш противника при наилучших (для нас) наших действиях
   
5. максимальная ставка игры
   

Математический анализ систем массового обслуживания облегчается если

1. процесс, протекающий в системе – дискретный
   
2. процесс, протекающий в системе – непрерывный
   
3. процесс, протекающий в системе – марковский
   
4. система имеет конечное число состояний
   

Абсолютная пропускная способность есть

1. математическое ожидание интенсивности обслуживания
   
2. номинальная производительность системы
   
3. максимальная производительность системы
   
4. отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок
   
5. среднее число заявок, которое может обслужить система в единицу времени
   

Транспортная задача с критерием времени классифицируется следующим образом

1. не является задачей ЛП, но может быть к ней сведена
   
2. является задачей ЛП
   
3. не является задачей ЛП и не решается методами ЛП
   
4. может быть сведена к нескольким задачам ЛП
   
5. сводится к задаче ЛП путем введения «добавочных переменных»
   

Процесс называется марковским, если

1. система может вернуться в предыдущее состояние
   
2. переход системы из состояния в состояние подчиняется нормальному закону распределения
   
3. система может переходить только в состояния с большими номерами
   
4. для каждого момента времени вероятность любого состояния системы в будущем зависит только от текущего состояния
   

Два игрока A и B не глядя друг на друга, одновременно кладут на стол по картонному кружку с цифрами. Игрок A кладет кружки с цифрами 1, 2, 3 или 4. Игрок B — с цифрами 1 или 2. После этого игроки расплачиваются друг с другом следующим образом: выигрыш равен сумме цифр, если она четная, то выигрыш получает игрок A иначе — игрок B. Платежная матрица этой игры имеет вид:

1. 
   
2. 
   
3. 
   
4. 
   
5. 
   

Нижней ценой игры называется

1. максимальный выигрыш при наилучших (для него) действиях противника
   
2. минимальная ставка хода
   
3. минимальный выигрыш при данной стратегии
   
4. минимальный проигрыш при данной стратегии
   
5. минимальная ставка игры
   

Формулировка принципа оптимальности: Оптимальная стратегия обладает свойством оптимальности

1. функции выигрыша на каждом шаге
   
2. на предыдущих шагах процесса
   
3. начиная с данного шага и до конца процесса
   
4. функции выигрыша на всех предыдущих шагах
   
5. функции выигрыша на всех последующих шагах
   

Чтобы свести задачу ЛП «на минимум» к задаче «на максимум» необходимо

1. взять дополнительную величину 1/L целевой функции
   
2. поменять знаки bj на – bj
   
3. взять обратную величину 1/L целевой функции
   
4. поменять знаки aij на – aij
   
5. поменять знак целевой функции
   

Процессом с дискретными состояниями называют процесс, в котором

1. имеется конечный набор состояний
   
2. переход из состояния в состояние производится в дискретные моменты времени
   
3. можно пронумеровать все возможные состояния системы, а переход из состояния в состояние осуществляется скачком
   
4. вероятность перехода из состояния в состояние описывается дискретной функцией распределения
   

Постановка задачи ЛП о пищевом рационе выполнена при условии

1. минимизации стоимости рациона
   
2. заданной диеты
   
3. сбалансированности питания
   
4. необходимого количества продуктов
   
5. необходимой пищевой ценности
   

Каждый из двух игроков A и B одновременно и независимо друг от друга записывает на бумаге любое целое число. Если сумма чисел четная, то игрок A получает от игрока B 2 руб., если нечетная — платит игроку B 2 руб. Платежная матрица этой игры имеет вид:

1. 
   
2. 
   
3. 
   
4. 
   
5. 
   

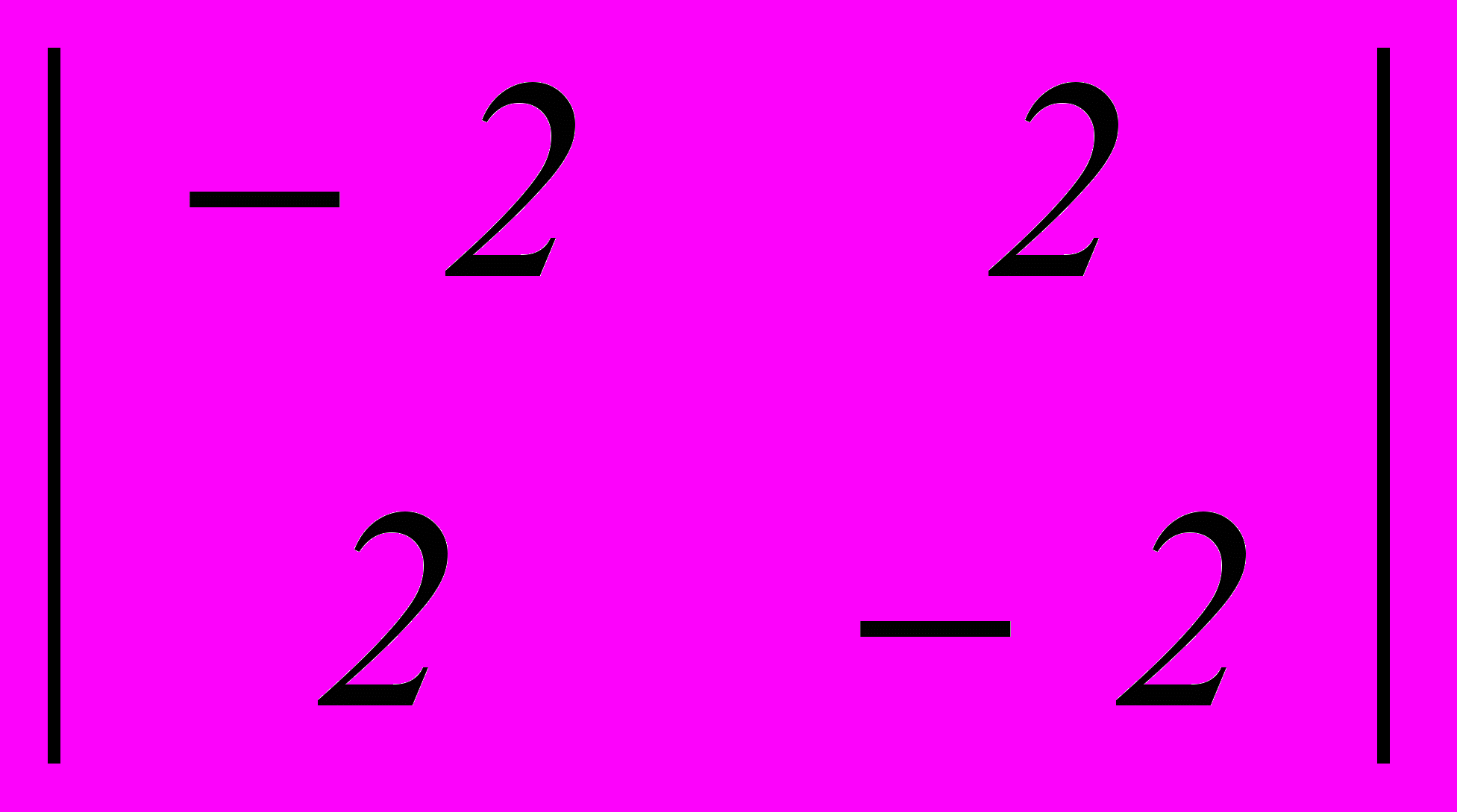Используя платежную матрицу , построить стратегию поведения игрока А, всегда приводящую к выигрышу

1. можно, всегда выбирая стратегию 1
   
2. нельзя
   
3. можно, всегда выбирая стратегию 2
   
4. можно, чередуя стратегии 1 и 2
   
5. можно, используя механизм случайного выбора
   

Условно-оптимальное управление оптимизирует функцию

1. сумму всех пошаговых выигрышей
   
2. выигрыша на данном шаге
   
3. сумму выигрышей на данном и всех предыдущих шагах
   
4. условного оптимального выигрыша
   
5. сумму выигрышей на данном и всех последующих шагах
   

Временным сетевым графиком называется сетевой график,

1. упорядоченный по времени выполнения работы
   
2. на котором проставлена длительность работы
   
3. построенный вдоль временной оси с учетом длительности работ
   
4. на котором длина стрелки пропорциональна длительности работы
   

Постановка задачи ЛП о распределении ресурсов выполнена при условии

1. минимальных (общих) затрат
   
2. максимальной прибыли
   
3. максимальном удовлетворении спроса
   
4. использовании всех ресурсов
   
5. минимальной себестоимости