Взаимосвязь электрических и магнитных свойств в сильно коррелированных электронных системах оксидов и халькогенидов переходных металлов 01. 04. 07 физика конденсированного состояния

Вид материала

Автореферат диссертации

Содержание В шестой главе

Подобный материал:

• Синтез, оптические спектры и стереоатомный анализ структуры сложных халькогенидов,, 855.77kb.
• Трансформация структуры и электрофизических свойств оксидов переходных металлов при, 367.4kb.
• Учебно-методический комплекс по дисциплине Физика Конденсированного Состояния Для специальности, 322.8kb.
• Паспорт специальности 01. 04. 07 – физика конденсированного состояния, 1004.81kb.
• Эффект Холла и магнетосопротивление неупорядоченных магнитных систем на основе кремния, 334.2kb.
• Ён Викторович Методы визуализации кинетики зарождения и роста углеродных наноструктур, 219.01kb.
• Рабочая программа учебной дисциплины «Физика конденсированного состояния, термодинамика,, 223.9kb.
• Аннотация дисциплины «Магнетизм конденсированного состояния», 11.15kb.
• Министерство образования Российской Федерации международный университет природы, общества, 1374.95kb.
• Аннотация дисциплины, 39.03kb.

Пятая глава посвящена изучению механизмов взаимосвязи зарядовых и магнитных степеней свободы при изменении концентрации носителей заряда. Изучены концентрационные переходы в сериях оксисульфидов (VS)_x(Fe₂O₃)_2-x, сульфидов Fe_xV_1-xS, хромовых шпинелей Cu_xZn_1-xCr₂Se₄ и Cd_xHg_1-xCr₂Se₄.

Кристаллическая структура оксисульфидов (VS)_x(Fe₂O₃)_2-x при х близком к единице аналогична родственному соединению – магнетиту.

О


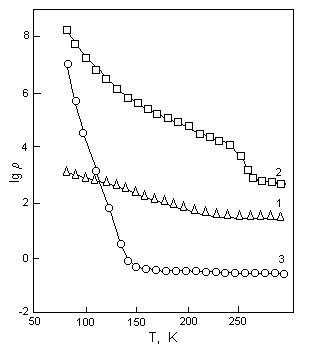
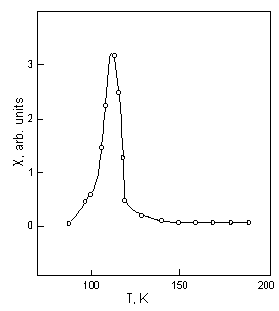
Рис. 14. Температурные зависимости удельного сопротивления  образцов (VS)_x(Fe₂O₃)_2-x. 1 – х = 0.9, 2 – 1.1, 3 – 1.25 (слева).

Температурная зависимость магнитной восприимчивости  образца (VS)_x(Fe₂O₃)_2-x при х = 1.25 (справа).



ксисульфидные соединения (VS)_x(Fe₂O₃)_2-x при х = 0.9 и 1.1 характеризуются немонотонными температурными зависимостями магнитной восприимчивости с широкими максимумами в окрестности 150 и 300 К. Сопротивление этих составов слабо зависит от температуры (рис. 14). Выраженной взаимосвязью магнитных и электрических свойств обладает состав с х = 1.25. Магнитная восприимчивость этого соединения имеет резкий пик при Т = 115 К (рис. 14). В близкой области температур происходит переход металл–диэлектрик. В температурном интервале 80-150 К сопротивление образца меняется на 8 порядков. И магнитный переход, и переход в проводимости (VS)_x(Fe₂O₃)_2-x при х = 1.25 происходят при температурах, близких к температуре Вервея (зарядового упорядочения) в структурно родственном соединении – магнетите Fe₃O₄. В этой же температурной области (VS)_1.25(Fe₂O₃)_0.75 испытывает структурный переход с понижением симметрии. Эти факты дают возможность предположить установление зарядового упорядочения в исследуемом оксисульфиде.

Для соединения VS ·Fe₂O₃ можно предположить следующую валентную формулу: 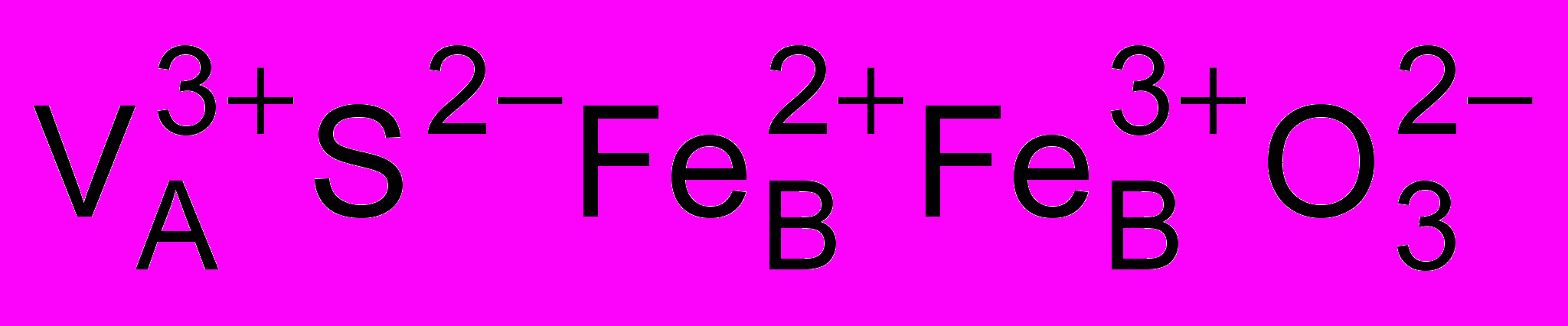. Ион V³⁺ в тетраэдрической позиции обладает двумя d-электронами на e_g – орбиталях. В кристалле e_g– зона, образованная этими орбиталями будет наполовину заполненной. Вследствие сильных корреляций e_g– зона ванадия расщепляется на нижнюю и верхнюю хаббардовские подзоны, причем для х = 1 уровень Ферми попадает в щель Мотта – Хаббарда. В составах с х < 1 e_g зона будет заполнена менее чем наполовину, а при х > 1 более чем наполовину. Носителями заряда при этом будут сильно коррелированные электроны обобществленных узких d-зон железа и ванадия, для которых характерны переходы между локализованными и делокализованными состояниями. Слабая температурная зависимость восприимчивости паулиевского типа, имеющая место для составов со степенью замещения х = 0.9 и х = 1.1 при высоких температурах указывает на делокализованный характер d – электронов. С понижением температуры, по мере проявления полупроводникового типа проводимости, температурная зависимость восприимчивости также становится более характерной для локализованных электронов.

Моносульфиды переходных металлов обычно кристаллизуются в структурных типах никелина NiAs. Ионы переходного металла находятся в октаэдрическом окружении серы. Крайние соединения изоструктурного ряда Fe_xV_1-xS обладают различным магнитным порядком. При температурах ниже комнатной FeS – антиферромагнетик, а VS парамагнитен.



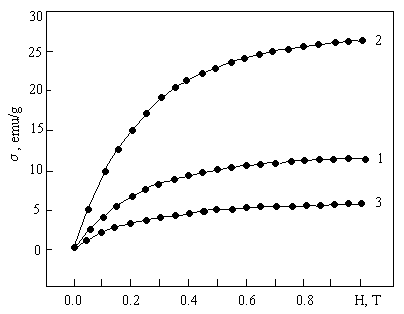
Рис. 15. Кривые намагничивания образцов Fe_xV_1-xS. 1 – х = 0.1, 2 – 0.2, 3 – 0.4, Т = 300 К (слева). Концентрационные зависимости магнитного момента на формульную единицу и температуры Кюри для Fe_xV_1-xS_. (справа).

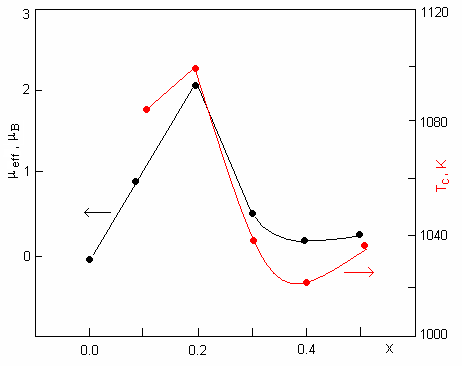
При исследовании твердых растворов Fe_xV_1-xS выяснилось, что составы с х < 0.1 парамагнитны, тогда как системы с большим содержанием железа испытывают переход в магнитоупорядоченное состояние (рис. 15), парамагнитная температура Кюри  = 1000-1100 К. По мере увеличения концентрации железа магнитный момент, приходящийся на формульную единицу изменяется немонотонно. В структурном плане система Fe_xV_1-xS может быть сопоставлена с системой V_1-xS. Частично заполненные а1 и e_g – орбитали железа Fe²⁺(d⁶) вместе с орбиталями V²⁺(3d³) и S^2- формируют зонную структуру близкую к α – VS (в парафазе). Частично заполненный e_g – дублет на ионе Fe²⁺ образует локализованный магнитный момент со спином S = 1. При малых х примеси Fe можно считать независимыми, и момент равен 2μ_B. С ростом х взаимодействие между примесями приведет к их магнитному упорядочению. При этом возрастет и перекрытие e_g – волновых функций ионов железа, что приводит к делокализации и уменьшению величины магнитного момента. Это предположение подтверждается и характером поведения температурных зависимостей электропроводности, которые изменяются от полупроводникового к температурно-независимому типу c ростом концентрации замещения ванадия на железо (рис. 16).




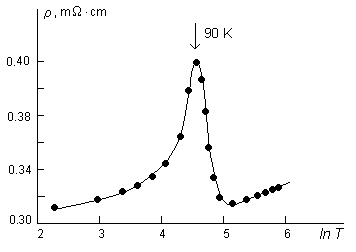
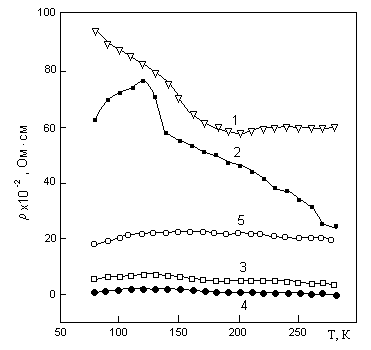
Рис. 16. Температурные зависимости удельного сопротивления составов Fe_xV_1-xS с х = 0.005 (слева) и х = 0.1 (1), 0.2 (2), 0.3 (3), 0.4 (4), 0.5 (5) (справа).

Своеобразное поведение проводимости продемонстрировал состав с очень малым содержанием железа х = 0.005. Температурная зависимость сопротивления этого состава имеет резкий пик при Т = 90 К (рис. 16), что характерно для проявления эффекта Кондо в системах с магнитными примесями. Известно, что при установлении магнитного порядка в системе эффект Кондо подавляется.

Наблюдаемый в данной работе переход между режимом Кондо и дальним магнитным порядком происходит при критической концентрации примесей х_С такой, что Т_К ~ х_Сθ_С, где Т_К – температура Кондо, θ_С – температура Кюри концентрированной магнитной системы. В нашем случае Т_К ~ 100 К, θ_С ~ 1000 К, так что х_С ~ 0.1.

В заключительной части главы рассмотрена взаимосвязь магнитных и электрических свойств, проявляющаяся при катионном замещении в смешанных хромовых шпинелях Cd_xHg_1-xCr₂Se₄ и Cu_xZn_1-xCr₂Se₄. Халькогенидные шпинели хрома в зависимости от состава могут демонстрировать различные типы магнитного упорядочения и особенности кинетических свойств. В связи с этим представляет интерес проследить, как изменяются физические свойства по мере замены одного катиона на другой.

Ранее было обнаружено, что появление ферромагнетизма в Cu_xZn_1-xCr₂Se₄ происходит при х  0.2, причем Т_С плавно растет по мере увеличения концентрации меди. Также известно, что составы с х < 0.1 антиферромагнитны, однако механизм перехода от неколлинеарного антиферромагнетизма к ферромагнетизму оставался невыясненным. Цель данной работы – детально исследовать область концентрационного магнитного перехода. Были измерены температурные и магнитополевые зависимости намагниченности и проводимости поликристаллических образцов Cu_xZn_1-xCr₂Se₄ в интервале концентраций х = 0.1 – 0.2 с шагом 0.02.

Измерения температурной зависимости магнитной восприимчивости и намагниченности показали, что образцы с х  0.12 парамагнитны при Т > 80 К, а остальные обладают значительным спонтанным магнитным моментом. Для всех образцов, как испытывающих магнитный переход в точке Т_С, так и нет, на кривой М(Т) имеется пик в Т_N  22 К (рис. 17).

Неожиданным образом повела себя концентрационная зависимость температуры Кюри образцов. В противоположность ранее известным данным для концентраций меди больших 0.2, Т_С не росла, а уменьшалась с ростом х (рис. 17). Для образца с х = 0.2 Т_С  370 К в соответствии с литературными данными. Для образца с х = 0.14 Т_С = 415 К, как в случае незамещенной шпинели CuCr₂Se₄.



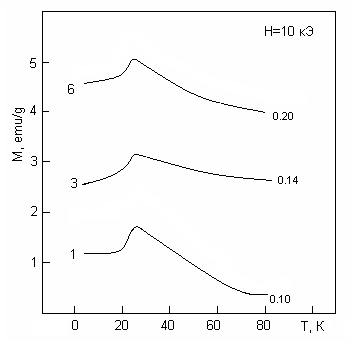
Рис. 17. Температурные зависимости намагниченности Cu_xZn_1-xCr₂Se₄ (слева). Значения х приведены на рисунке.

Температуры Кюри и Нееля твердых растворов Cu_xZn_1-xCr₂Se₄. Концентрационная зависимость (справа). 1 – наши данные, 2 – данные [8].


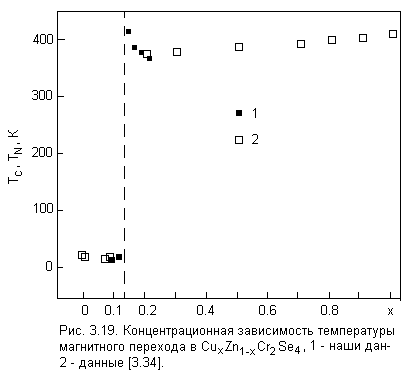
Ранее фазовая диаграмма Cu_xZn_1-xCr₂Se₄ интерпретировалась в терминах конкурирующих обменных взаимодействий, и для объяснения механизма концентрационного магнитного перехода предлагалась сложная цепочка концентрационных магнитных фазовых превращений: простая спираль – ферромагнитная спираль – спиновое стекло – ферромагнитная спираль – коллинеарный ферромагнетик [8]. Существование неколлинеарного спинового упорядочения в катионзамещенном ZnCr₂Se₄ при некоторых значениях концентрации и температуры подтверждено нейтронографическими данными. Однако наличие сателлитных линий в нейтронных спектрах может быть связано не только с неколлинеарной магнитной структурой образца, но и с двухфазным состоянием, когда образец представляет собой смесь ферромагнитных и антиферромагнитных областей. В работах Э.Л. Нагаева [9] теоретически обоснована меньшая устойчивость неколлинеарных систем по сравнению с коллинеарными, особенно при повышенных температурах и малых концентрациях. В связи с этим нельзя быть уверенным, что именно неколлинеарные магнитные структуры реализуются в Cu_xZn_1-xCr₂Se₄ в широкой области концентраций и температур.

По мере введения в ZnCr₂Se₄ атомов меди происходит переход части ионов хрома, находящихся в состоянии 3+, в состояние 4+. Реализуется состояние с переменной валентностью. При этом вокруг примесных ионов могут образовываться ферромагнитные области, не связанные между собой. С ростом концентрации примеси при некотором критическом значении х_С ФМ-область становится односвязной, устанавливается макроскопическое ФМ-упорядочение с температурой Кюри Т_С. С этого момента антиферромагнитные области присутствуют в ФМ-матрице в виде включений. Именно этот механизм, по-видимому, проявляется в исследуемых нами образцах с х > 0.12, для которых мы наблюдаем магнитные переходы как в Т_N, так и в Т_С. При этом антиферромагнитный пик в этих образцах наблюдается на фоне ферромагнитного вклада. Согласно нашим данным значение критической концентрации х_С  0.12 – 0.14. В пользу разделения фаз свидетельствуют также данные по проводимости образцов (рис. 18).



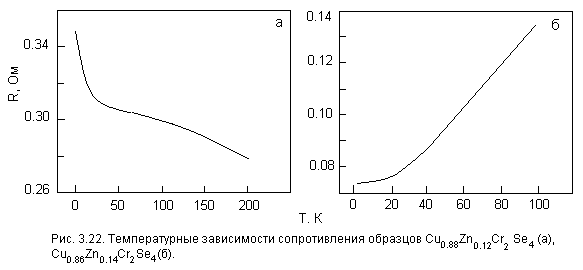
Рис. 18. Температурные зависимости сопротивления образцов Сu_0.12Zn_0.98Cr₂Se₄ (a) и Cu_0.14Zn_0.86Cr₂Se₄ (б).
В критической области концентраций происходит переход от полупроводникового типа проводимости к проводимости металлического типа. Таким образом, экспериментальные данные в области концентрационного перехода могут быть описаны на основе представлений о разделении фаз.

Резюме к пятой главе: в сильно коррелированных электронных системах взаимосвязь магнитных и зарядовых степеней свободы может проявляться не только при изменяющихся температуре или магнитном поле, но и в зависимости от концентрации носителей заряда. Механизмами, ответственными за взаимосвязь магнитных и электрических свойств при этом могут быть зарядовое упорядочение ((VS)_x(Fe₂O₃)_2-x), переход от режима Кондо к магнитному порядку (Fe_xV_1-xS) и фазовое расслоение (Cu_xZn_1-xCr₂Se₄).

В шестой главе представлены результаты изучения особенностей механизмов взаимосвязи магнитных и электрических свойств оксидов с двумя типами магнитных ионов. Исследование проведено на примере РЗМ-кобальтитов GdCoO₃ и SmCoO₃.

Кобальтиты редкоземельных элементов с общей формулой LnCoO₃ (Ln = La, Y, Sm, Gd, Eu…) являются перовскитоподобными кристаллами c октаэдрическим кислородным окружением переходного иона Со³⁺. Окружение редкоземельного иона в LnCoO₃ имеет более низкую симметрию С_s. Базовым и наиболее изученным соединением ряда является LaCoO₃, хорошо известное в связи со знаменитой проблемой высоко-, низко- и промежуточноспинового состояния ионов Со³⁺. Известно, что спиновое состояние Со³⁺ в LaCoO₃ может изменяться в зависимости от давления и температуры. В связи с давно идущей дискуссией по поводу устойчивости этих состояний вопрос о магнетизме редкоземельных элементов обычно остается в тени. Данная работа частично восполняет этот пробел.

Считается, что при температурах ниже комнатной во всех соединениях ряда LnCoO₃ (Ln ≠ La) ионы кобальта находятся в немагнитном низкоспиновом состоянии. За магнетизм этих соединений при низких температурах в основном ответственны РЗ-элементы.

Известно, что переход ионов Со³⁺ в высокоспиновое состояние сопровождается делокализацией электронов и пиком в температурной зависимости энергии активации. Таким образом, он может быть обнаружен при измерении проводимости образцов. Для исследуемых соединений этот пик наблюдается в области температур 600-700 К (рис. 19).


Рис. 19. Температурная зависимость проводимости SmCoO₃ и GdCoO₃. На вставке: температурная зависимость энергии активации.


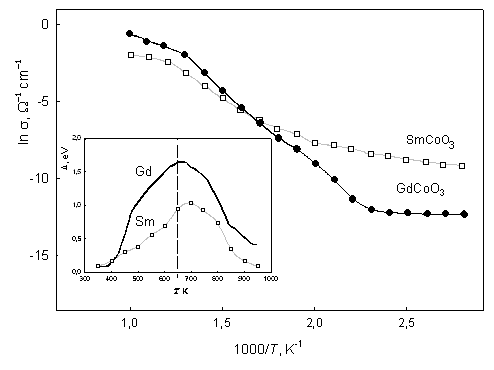Удельная электрическая проводи-мость образцов  при комнатной температуре имеет низкие значения порядка 10^-11 Ом^-1см^-1 для GdCoO₃ и 10^-9 Ом^-1см^-1 для SmCoO₃. При низких температурах оба состава могут быть отнесены к диэлектрикам.

Температурные зависимости статической магнитной восприимчивости  и обратной ей величины  ^-1 для GdCoO₃ и SmCoO₃ в магнитном поле напряженности Н = 1 kOe представлены на рис. 20. Видны несколько существенных различий. Во-первых, абсолютные значения восприимчивости SmCoO₃ на два порядка меньше, чем для GdCoO₃. Во-вторых, с ростом т

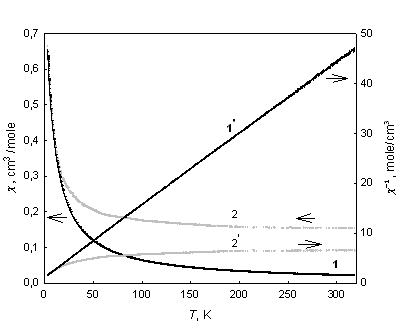
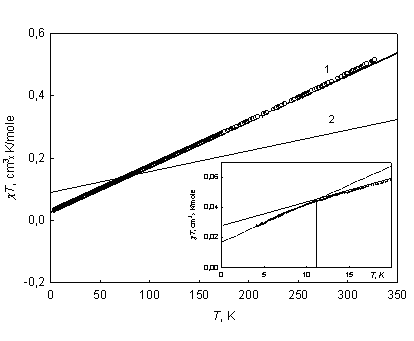
емпературы восприимчивость GdCoO₃ стремится к нулю, а у SmCoO₃ – к

Рис. 23. Температурные зависимости магнитной восприимчивости  и обратной ей величины образцов GdCoO₃ (кривые 1, 1’) и SmCoO₃ (кривые 2, 2’). Значения восприимчивости SmCoO₃ умножены на 100 (слева).

Температурная зависимость произведения Т для SmCoO₃. 1- эксперимент, 2 – зависимость, характерная для свободного иона Sm³⁺ (справа).

постоянному значению ₀ = 1.5410^-3 см³/моль. Наконец, для GdCoO₃ температурная зависимость обратной магнитной восприимчивости хорошо аппроксимируется прямой линией, что указывает на выполнение закона Кюри-Вейсса:  = С/(T+) (13)

Асимптотическая температура Кюри   –6 К, эффективный магнитный момент на формульную единицу _eff  7.38 _В. температурный ход обратной магнитной восприимчивости SmCoO₃ существенно нелинеен. Линейной является температурная зависимость произведения восприимчивости на температуру (рис. 20.) Это значит, что магнитная восприимчивость SmCoO₃ может быть представлена в виде суммы двух вкладов: подчиняющегося закону Кюри и температурно-независимого ₀:

 = C/T + ₀. (14)

На вставке к рис. 20, где показана низкотемпературная часть зависимости Т, видно, что прямая линия имеет излом в окрестности Т = 1011 К и выходит на другой участок, также близкий к линейному.

В РЗМ-кобальтитах LnCoO₃ расщепление энергетических уровней кристаллическим полем по порядку величины составляет 10² см^-1, что значительно превышает величины обменных, дипольных и других взаимодействий. Однако ион Gd³⁺ в этом смысле является одним из исключений, так как основным состоянием этого иона является S – состояние (4f ⁷, ⁸S_7/2, L = 0, S = 7/2), которое расщепляется кристаллическим полем только в высших порядках теории возмущений. Поэтому можно ожидать, что магнитные свойства ионов Gd³⁺ в GdCoO₃ будут близки к свойствам совокупности свободных ионов. Приблизительно так дело и обстоит в действительности. Тем не менее отрицательное значение  = – 6 К и заметно меньшая величина эффективного магнитного момента _eff = 7,38 _В по сравнению со значением 7.94 _В для свободного иона указывают на наличие слабого антиферромагнитного взаимодействия.

Что касается свободного иона Sm³⁺, то его электронная конфигурация 4f⁵, основное состояние – мультиплет ⁶Н_5/2 (L = 5, S = 5/2). Характерной особенностью этого иона является относительная близость к основному первого возбужденного состояния ⁶Н_7/2. Разность энергий этих состояний для свободного иона составляет примерно 1000 см^-1. Примешивание волновых функций возбужденных состояний к основному приводит к возникновению поляризационного парамагнетизма ван Флека. В ван-флековских парамагнетиках магнитная восприимчивость  может быть представлена в виде суммы трех слагаемых:  = _с + _p + _d, (15)

где _с – восприимчивость, обусловленная обычным ориентационным парамагнетизмом ионов в основном состоянии; _p – поляризационная ван-флековская восприимчивость и _d – диамагнитная компонента. Последнюю будем считать пренебрежимо малой. Ван-флековская восприимчивость тем больше, чем меньше разность энергий E_n’ – E_n основного и возбужденного состояний. Если нет теплового возбуждения вышележащих уровней, то _p не зависит от температуры.

Восприимчивость свободных ионов Sm³⁺, рассчитанная по формуле:

(Sm³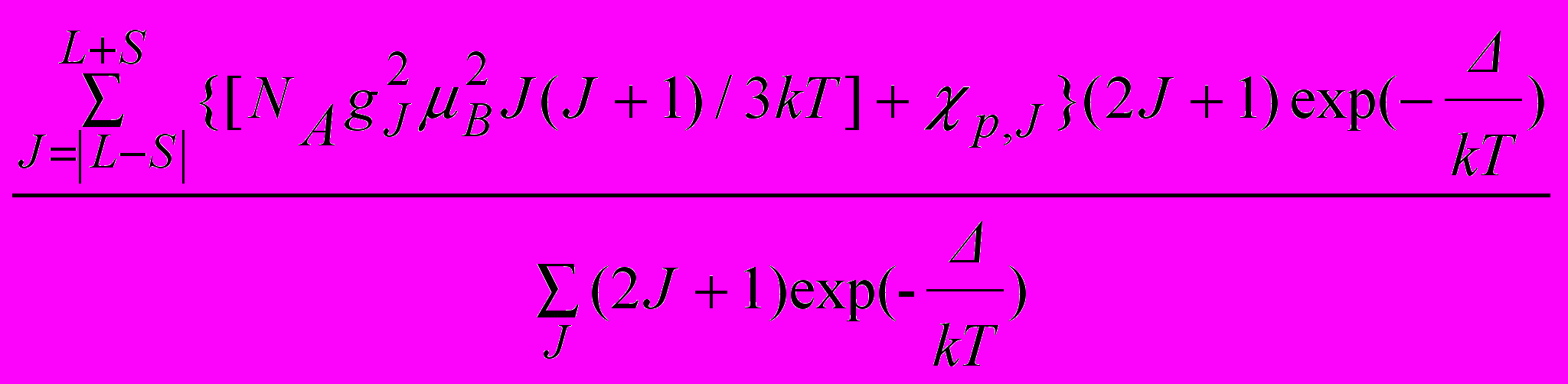⁺) = (16)

приведена на рис. 20 в координатах Т (Т) (линия 2). Учтены только два состояния – основное с J = 5/2 и g_5/2 = 2/7 = 0,2857 и первое возбужденное с J = 7/2 и g_7/2 = 0,8254. Величина  принята равной 1100 см^-1. Видно, что при температурах ниже комнатной получившаяся зависимость практически линейна, следовательно, термическим заселением состояния ⁶