Взаимосвязь электрических и магнитных свойств в сильно коррелированных электронных системах оксидов и халькогенидов переходных металлов 01. 04. 07 физика конденсированного состояния

Вид материала

Автореферат диссертации

Содержание Третья и четвертая главы Четвертая глава Т = 4.2 К в магнитополевой зависимости электросопротивления наблюдается слабопериодичный осциллирующий вклад R

Подобный материал:

• Синтез, оптические спектры и стереоатомный анализ структуры сложных халькогенидов,, 855.77kb.
• Трансформация структуры и электрофизических свойств оксидов переходных металлов при, 367.4kb.
• Учебно-методический комплекс по дисциплине Физика Конденсированного Состояния Для специальности, 322.8kb.
• Паспорт специальности 01. 04. 07 – физика конденсированного состояния, 1004.81kb.
• Эффект Холла и магнетосопротивление неупорядоченных магнитных систем на основе кремния, 334.2kb.
• Ён Викторович Методы визуализации кинетики зарождения и роста углеродных наноструктур, 219.01kb.
• Рабочая программа учебной дисциплины «Физика конденсированного состояния, термодинамика,, 223.9kb.
• Аннотация дисциплины «Магнетизм конденсированного состояния», 11.15kb.
• Министерство образования Российской Федерации международный университет природы, общества, 1374.95kb.
• Аннотация дисциплины, 39.03kb.

Вторая глава посвящена описанию объектов изучения, технологии их приготовления, методик исследования электрических и магнитных свойств материалов.

Монокристаллические образцы HgCr₂Se₄ были изготовлены в ИПФ АН МССР (г. Кишинев) и в ИОНХ АН СССР (г. Москва) методом химического транспорта в замкнутой системе. Максимальный размер кристаллов, получаемых этим методом, не превышает 5 мм. Для получения ртутной шпинели с n-типом проводимости образцы подвергались отжигу в парах ртути, что привело к вырождению электронного газа в интервале температур 1.8 – 100 К с холловской концентрацией порядка 10¹⁸ см^-3.

Образцы твердых растворов Cu_xZn_1-xCr₂Se₄, (VS)_x(Fe₂O₃)_2-x и Fe_xV_1-xS представляли собой порошкообразные поликристаллы, полученные по технологии твердофазного синтеза со ступенчатым отжигом и закалкой.

Монокристаллы FeBO₃, VBO₃, CrBO₃ и твердые растворы Fe_1-xV_xBO₃ были выращены методом спонтанной кристаллизации из раствора-расплава. Удалось получить монокристаллы в виде тонких пластин гексагональной формы размерами до 4х4 мм и толщиной около 0.1 мм с гладкой блестящей поверхностью. Для определения количества входящих элементов для всех образцов в Университете г. Кельн (Германия) был выполнен энерго-дисперсионный рентгеновский анализ. Анализ показал, что соединения смешанного состава V_xFe_1-xBO₃ имеют кристаллическую структуру кальцита, как и крайние члены ряда, и не испытывают структурного перехода при понижении температуры до 77 К.

Монокристаллы La₂CuO₄ были синтезированы в Институте кристаллографии АН СССР кристаллизацией из нестехиометрических растворов-расплавов с избытком CuO.

Поликристаллические кобальтоксидные соединения GdCoO₃ и SmCoO₃ были синтезированы в университете Гвадалахара (Мексика) золь-гель методом.

Измерения электросопротивления были выполнены четырехконтактным методом на основе компенсационных схем.

Измерения динамической магнитной восприимчивости выполнялись с использованием моста взаимной индукции и фазочувствительного детектирования. Чувствительность моста 10^-5 см³/г. Относительная погрешность измерений 0,1%.

Статические магнитные измерения выполнены на автоматизированном магнито-метре со сверхпроводящим соленоидом. Погрешность статических магнитных измерений равна 210^-5 Гссм³/г.

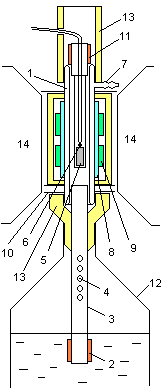
Криогенный эксперимент строился с использованием разработанных автором приставок к транспортным дьюарам с криоагентом, в том числе проточного типа (рис. 2). Погрешность стабилизации и измерения температуры составляет порядка 0.1 К, для проточных схем порядка 1 К.

П
Рис. 2. Криогенная измерительная ячейка

проточного типа.

1-кварцевая трубка

2, 11-нагреватели

3-стальная трубка

4-отверстия

5-образец

6-датчик температуры

7-штуцер

8-первичная катушка

9-вторичные катушки

10-тепловые экраны

12-дьюар

13-кожухи

14-электромагнит


огрешности, возникающие при измерениии электрического сопротивления сильно зависят от диапазона абсолютных значений измеряемых величин, поскольку приходится использовать различный приборный парк и применять различные схемные решения. Как правило, относительная погрешность измерения сопротивления в диапазоне 10^-6 ÷ 10⁶ Ом не превышает 0.1 %. Для очень больших сопротивлений погрешность измерения может достигать 5 % при сопротивлении большем 10¹⁰ Ом.

Третья и четвертая главы посвящены изучению проблемы формирования взаимосвязи магнитных и электрических свойств вследствие особенностей энерге-тической структуры, формируемых под действием сильных электронных корреляций. Проведено сравнительное изучение соединений переходных металлов со слабой и сильной взаимосвязью электронной и магнитной подсистем. В качестве примера первых соединений выступают бораты переходных металлов МВО₃ (М = Fe, V, Cr), как пример вторых – магнитные полупроводники халькогенидные шпинели хрома n-HgCr₂Se₄ и купрат лантана La₂CuO₄.

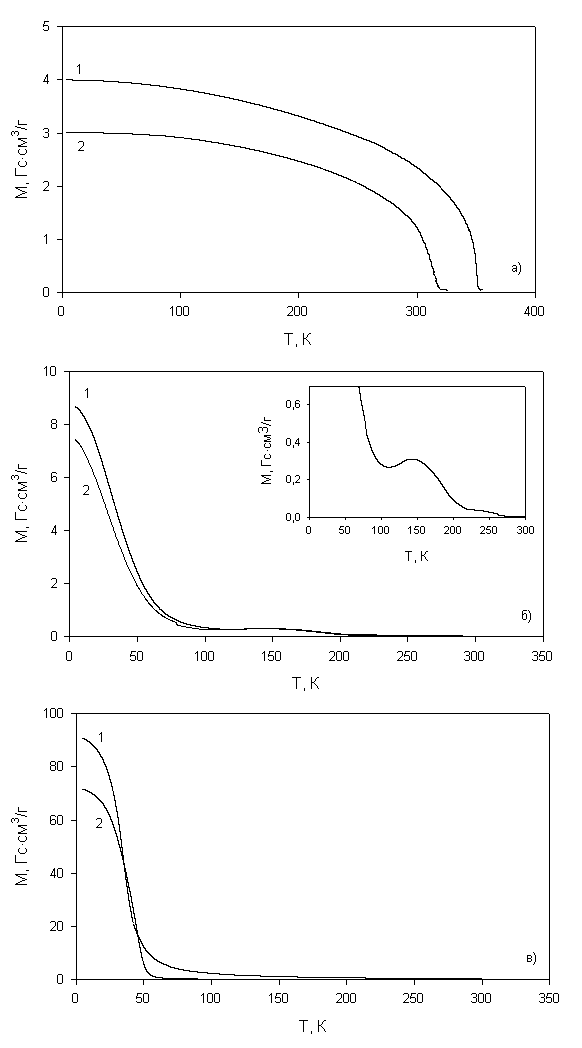
Кратко остановимся на результатах, касающихся боратов 3d-металлов и описанных в третьей главе. Для монокристаллов Fe_1-xV_xBO₃ были проведены комплексные исследования магнитных, электрических и оптических свойств. Температурные зависимости намагниченности твердых растворов Fe_1-xV_xBO₃ приведены на рис. 3 вместе с кривыми, соответствующими крайним членам ряда.

Известно, что FeBO₃ – слабый ферромагнетик. Температурная зависимость намагниченности VBO₃ типична для ферромагнетиков и в спин-волновой области хорошо описывается законом Блоха:

M(T) = M(0)(1-T^3/2). (1)

При замещении всего 5% ионов V на Fe магнитный момент уменьшается на 20%. Кривые намагничивания образцов с промежуточной концентрацией (х = 0.18, 0.3) имеют нетривиальный вид (рис. 3 (б)). В области температур, близких к температуре Кюри VBO₃, намагниченность быстро падает, и ее значение составляет 9% от величины, характерной для незамещенного соединения. В районе Т = 150 К наблюдается широкий максимум, затем намагниченность уменьшается до нуля вблизи температуры Нееля FeBO₃. Вероятно, что при малых концентрациях ионов железа механизм конкуренции обменных взаимодействий приводит к возникновению неколлинеарных спиновых структур, в которых угол скоса подрешеток может меняться в зависимости от концентрации и температуры. При больших концентрациях железа в системе превалирует магнитная структура, характерная для FeBO₃.

М
Рис. 3. Температурные зави-симости намагниченности в поле Н=10 кЭ; a) FeBO₃ (1), Fe_0.87V_0.13BO₃ (2); б) Fe_0.82V_0.18BO₃ (1), Fe_0.7V_0.3BO₃ (2); в) VBO₃ (1), Fe_0.05V_0.95BO₃ (2).
онокристалл VBO₃ и твердые растворы Fe_1-xV_xBO₃ с концентрациями х = 0.18, 0.3, 0.95 обладают низкой проводимостью при комнатной температуре (  10⁶÷10⁷ Омсм), в то время как образцы, более близкие по составу к FeBO₃, можно отнести к диэлектрикам. Измерения показали, что в области высоких температур (Т > 300 К) прохождение тока определяется носителями заряда, термически возбужденными в зону проводимости. В этом случае сопротивление описывается простым активационным законом с энергией активации порядка 1 эВ (рис. 4 (а)). При понижении температуры наблюдаются отклонения от активационного закона и переход к температурной зависимости, характерной для закона Мотта (рис. 4 (б)): R(T)  exp(T₀/T)^1/4, (2)

г
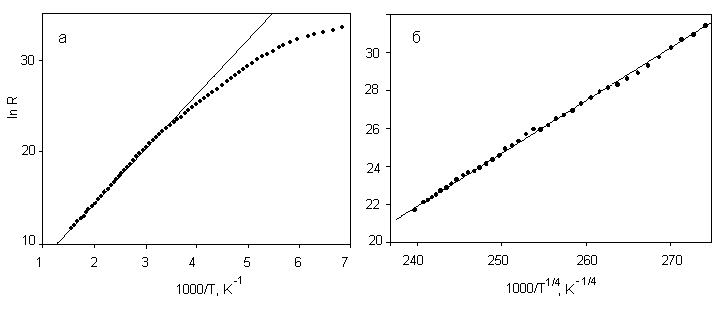
де Т₀ – характеристическая температура, определяющая плотность


Рис. 4. Температурные зависимости сопротивления Fe_0.82V_0.18BO₃.

состояний на уровне Ферми N(E_F).

Температурные зависимости сопротивления не проявляют каких-либо аномалий в точках, соответствующих аномалиям намагниченности. В исследуемом температурном интервале также не удалось обнаружить заметного магнитосопротивления. Таким образом, в боратах электрические и магнитные свойства взаимосвязаны слабо.

С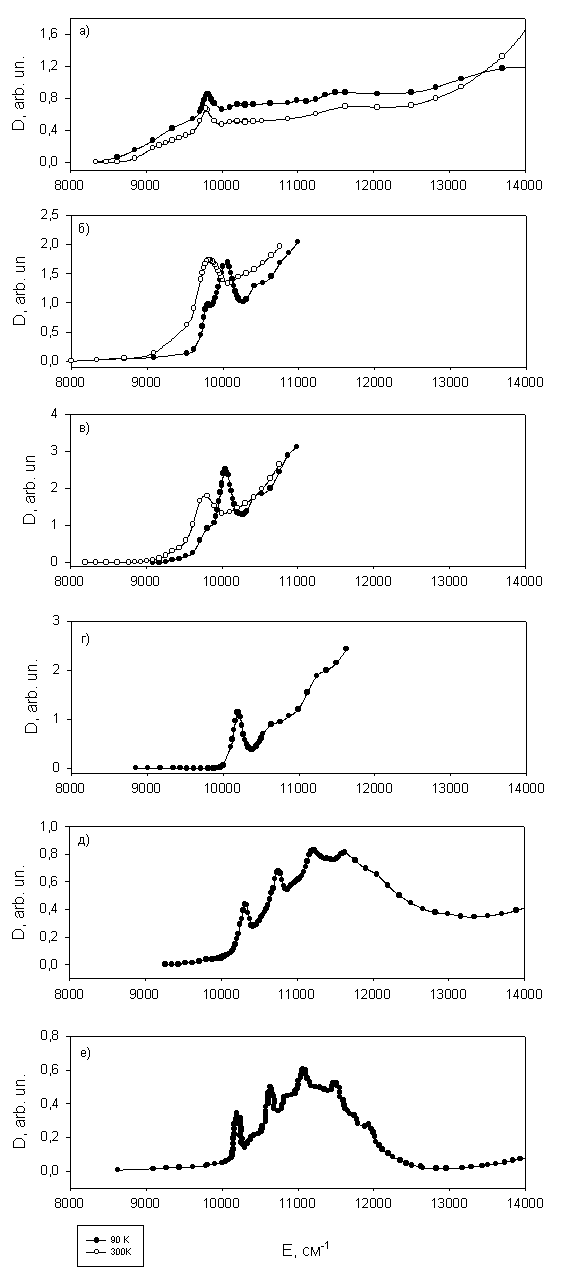пектры оптической плотности D = ln(I₀/I), полученные при температурах 90 и 300 К приведены на рис. 5. Для кристалла VBO₃ виден слабый, не зависящий от температуры пик 9800 см^-1. Этот пик сохраняется при низких температурах в спектрах образцов с промежуточной концентрацией х = 0.3 и х = 0.18 , но также появляется новый пик 10100 см^-1 с ярко выраженной температурной зависимостью (рис. 5(б) и (в)). При повышении температуры эта линия уширяется и сдвигается в область меньших энергий. Для кристалла с х = 0.23 этот пик остается, а линия, характерная для VBO₃, исчезает (рис. 5(г)). Спектр кристалла с малым замещением железа качественно повторяет спектр FeBO₃, состоящий из широкой полосы с центром на 11500 см^-1 и наблюдающейся на ее фоне серии узких линий. Для бората железа эти линии интерпретируются как фононные повторения экситон-магнонной полосы (низкочастотный переход ⁶А_1g  ⁴T_1g).


Рис. 5. Кривые оптического поглощения: а) VBO₃; б) Fe_0.7V_0.3BO₃; в) Fe_0.82V_0.18BO₃; г) Fe_0.87V_0.13BO₃; д) Fe_0.98V_0.02BO₃; e) FeBO₃.
Для расчета плотности состояний N(E) с учетом сильных электронных корреляций в VBO₃ в рамках многоэлектронной модели рассмотрим заполненный терм V³⁺ (3d²) и термы конфигураций 3d¹ и 3d³, описывающие уничтожение и рождение электрона из d². Для простоты пренебрегаем орбитальной зависимостью кулоновских матричных элементов, считая что параметры U, V и J связаны между собой известным следствием сферической симметрии атома U = 2V+J (U_ и V_’ соответствуют кулоновскому внутриорбитальному и межорбитальному отталкиванию, а J_’ – хундовскому обмену). Поскольку расстояния металл–кислород в октаэдрах VBO₃ и FeBO₃ близки, можно предположить, что кулоновские параметры для VBO₃ имеют те же значения, что и в FeBO₃: U = 3 эВ, V = 1.15 эВ, J = 0.7 эВ. Гамильтониан модели имеет вид:

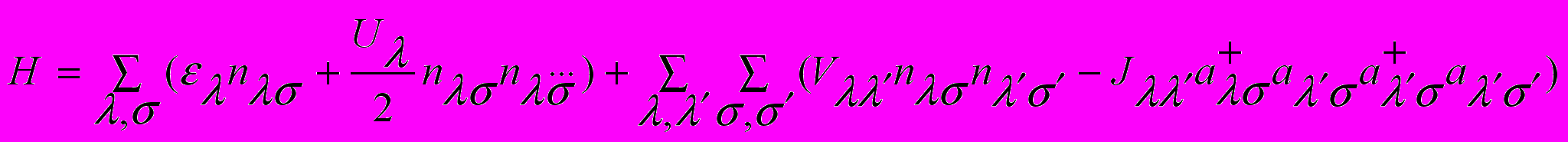(3)

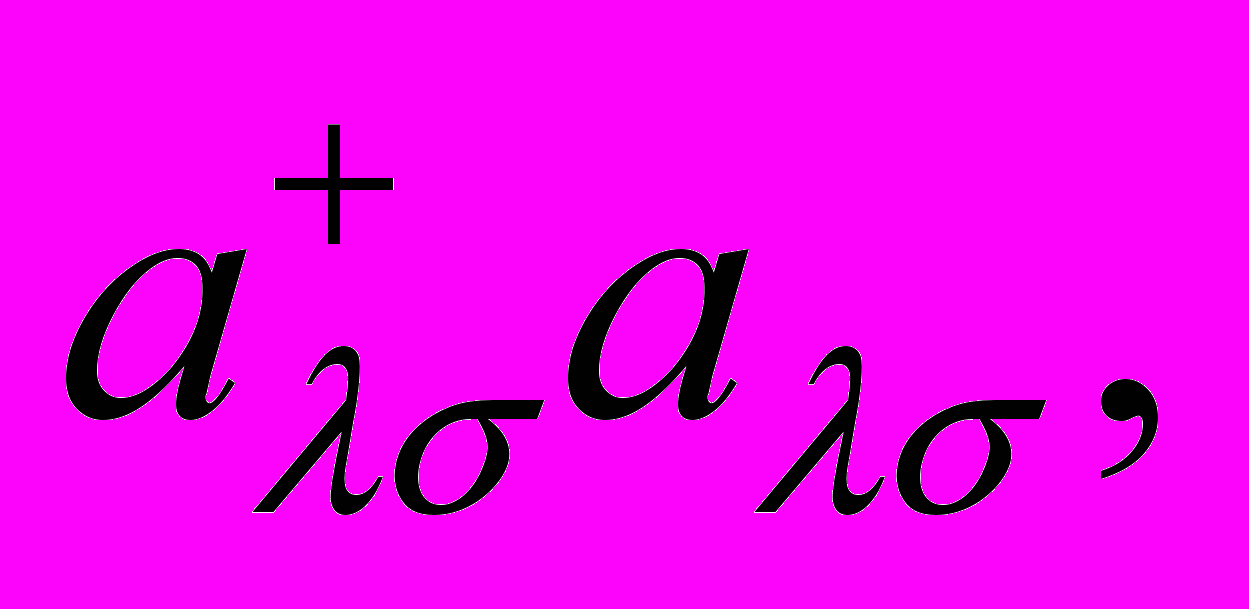
где n_ = _ обозначает оператор рождения d-электрона на одной из 5-ти орбиталей  c проекцией спина . Первое слагаемое описывает атомные d-уровни в кристаллическом поле. Параметр кристаллического поля можно определить из спектра оптического поглощения VBO₃, полагая, что пик на энергии ₀ = 9800 см^-1 обусловлен d-d переходами с основного терма ³Т₁ иона V³⁺ в первый возбужденный терм ³Т₂ с энергией  =1.21 эВ. Уровни _с и _v – аналоги верхней и нижней хаббардовских зон при нулевом межатомном параметре перескока t и равны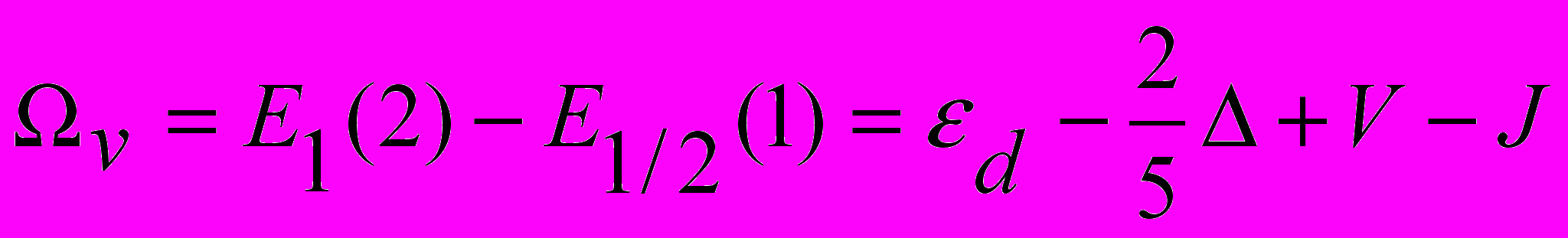

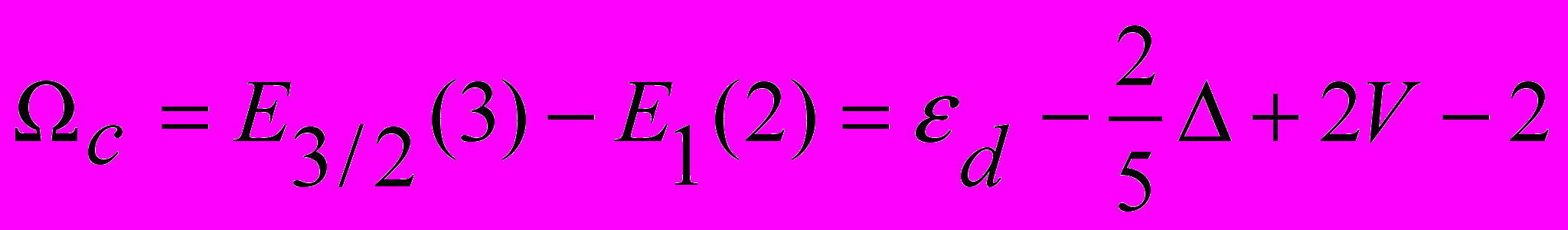(4)

Переход d²d¹ определяет рождение дырки, преход d²d³ рождение электрона. Кроме уровней _v и _с со спектральным весом равным единице, в многоэлектронном подходе появляются виртуальные уровни с нулевым в стехиометрическом основном состоянии спектральным весом (на рис. 1 и 6 отмечены пунктиром). Такие состояния приобретают спектральный вес при отклонении от стехиометрии или при оптической накачке возбужденных уровней. Для привязки уровней _v и _с к краям зон использовались данные по электропроводности и оптическому поглощению. Для VBO₃ эффективная энергия Хаббарда Ueff = _с - _v = 0.45 эВ. Исходя из соотношения между эффективной хаббардовской энергией и энергией энергией переноса заряда согласно классификации Заанена-Завадского-Аллена VBO₃ можно отнести к диэлектрикам Мотта-Хаббарда, в противоположность FeBO₃, относящемуся к диэлектрикам с переносом заряда.

П
Рис. 6. Схема плотности состояний твердых растворов Fe_1-xV_xBO₃. Левая часть входит с весом х, правая – с весом 1-х.

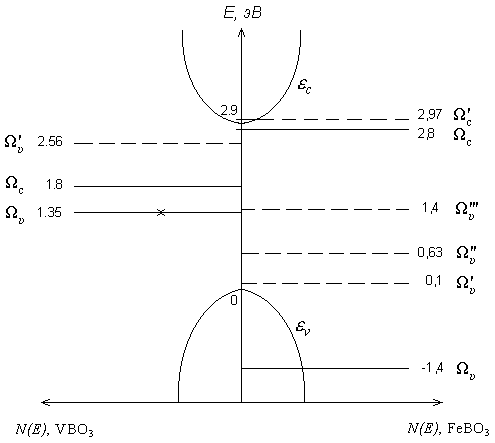
ри простейшем моделировании зонной структуры твердых растворов Fe_1-xV_xBO₃ сделаем следующие допущения: 1) положение дна зоны проводимости и потолка валентной зоны, а также величина щели постоянны при всех х; 2) в образце имеет место случайное расположение ионов V³⁺ с концентрацией х и ионов Fe³⁺ с концентрацией 1-х. В этой модели плотность состояний и оптическая плотность будут иметь вид:

N(E)=xN_V(E)+(1-x)N_Fe(E),

D()=xD_V()+(1-x)D_Fe() (5)

Плотность состояний твердых растворов изображена на рис. 6. Анализ спектров оптического поглощения, проведенный на основе предложенной модели, показыает, что для х = 0.02 вклад от ионов ванадия в оптическое поглощение пренебрежимо мал, и спектр на рис. 5(д) практически совпадает со спектром FeBO₃. Для х = 0.3 и 0.18 в экспериментальных спектрах можно выделить те же линии А₁-А₄, что и в FeBO₃, но сильно уширенные. В неупорядоченном магнитном состоянии FeBO₃ линия 9950 см^-1 очень близка к линии поглощения VBO₃ 9800 см^-1, поэтому для твердых растворов имеет место наложение двух близких по энергии линий, и в спектре поглощения виден широкий пик. С понижением температуры до 90 К в спектре поглощения возникает расщепление линий благодаря влиянию магнитного упорядочения в FeBO₃. Таким образом, многоэлектронная модель энергетической структуры боратов с учетом сильных электронных корреляций позволяет качественно воспроизвести спектры поглощения твердых растворов Fe_1-xV_xBO₃, а также описать электрические свойства этих материалов.

По результатам исследования взаимосвязи магнитных и электрических свойств боратов можно сделать следующее заключение: в данных соединениях эта взаимосвязь выражена слабо, несмотря на большую величину s-d обменного взаимодействия. Возможной причиной являются особенности электронной структуры, такие как большая ширина диэлектрической щели и отсутствие энергетической близости локализованных и коллективизированных электронных состояний.




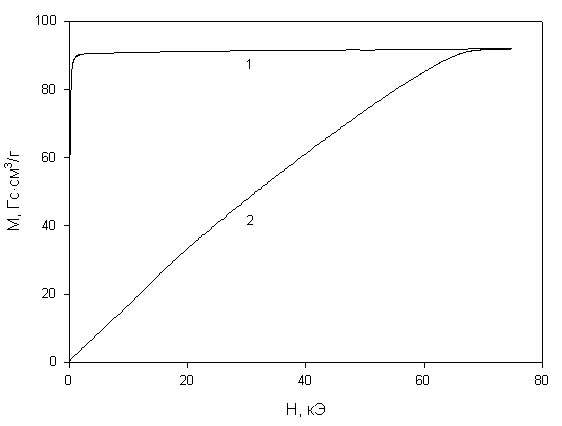
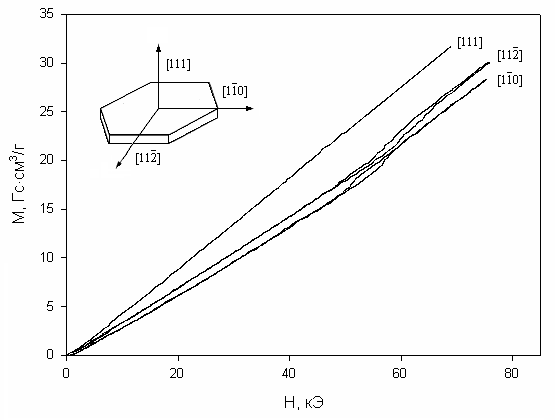
Рис. 7. Кривые намагничивания VBO₃ (слева) и CrBO₃ (справа). Для VBO₃ 1– намагничивание вдоль оси с [111], 2 – намагничивание в базисной плоскости.

Поскольку оксибораты VBO₃, CrBO₃ являются малоизученными, были проведены сопутствующие исследования их магнитной структуры. Кристалл VBO₃ – типичный ферромагнетик с температурой Кюри 30-32 К, тогда как соединение CrBO₃ антиферромагнитно, температура Нееля составляет 15 К. Поведение намагниченности монокристалла VBO₃ характерно для ферромагнетика типа “легкая плоскость” (рис. 7). Анизотропия в плоскости очень мала. Температурная зависимость первой константы одноосной анизотропии К₁ хорошо описывается в рамках классической теории магнитной анизотропии, в которой К₁(Т) пропорциональна третьей степени намагниченности К₁(Т) = К₁(0)(М(Т)/M_s)³, (6)

где M_s – намагниченность насыщения. Поле одноосной анизотропии равно Н_а = 62.5 кЭ. Эта величина является наибольшей в ряду изоструктурных соединений. Возможной причиной большой одноосной анизотропии VBO₃ является сильное спин-орбитальное взаимодействие, поскольку основным состоянием иона V³⁺ является F-состояние.

Монокристаллы CrBO₃ были выращены в форме правильных гексагональных пластинок. В отличие от изоструктурных FeBO₃ и VBО₃, кривые намагничивания CrBO₃ при намагничивании в базисной плоскости сопровождаются гистерезисом и шумами (рис. 7), что указывает на значительную гексагональную анизотропию в этом соединении. Следовательно, магнитная структура кристалла CrBO₃ не может быть описана на основе простой модели коллинеарного двухподрешеточного антиферромагнетика с магнитными моментами, лежащими вдоль оси с. Более вероятно, что вектор антиферромагнетизма лежит в плоскости, близкой к базисной. Величина эффективного обменного поля в CrBO₃ H_ex = 382 кЭ.

Четвертая глава посвящена изучению соединений, в которых взаимосвязь магнитной и электронной подсистем, в противоположность боратам, выражена очень сильно. Механизмы формирования этой взаимосязи рассмотрены на примере двух классов материалов – халькогенидных шпинелей хрома n-HgCr₂Se₄ и купрата лантана La₂CuO₄.

Магнитные полупроводники с общей формулой АCr₂Х₄ ( А = Cd, Hg, Zn, Cu ...; X = S, Se, Te) имеют пространственную структуру шпинели. Для тройных полупроводников со структурой шпинели характерна ситуация, когда зона проводимости коллективизированных s- электронов и локализованные d-состояния близки по энергиям (рис. 1). Этот результат получается, как в многоэлектронной модели [3], так и в одноэлектронном зонном расчете [4]. В случае вырождения результирующее электронное состояние будет суперпозицией этих состояний. Понятие валентности теряет при этом свой первоначальный смысл, и становятся возможными состояния с нецелочисленной или промежуточной валентностью. В случае селенодефицитного n-HgCr₂Se₄ есть основание предполагать наличие разновалентных конфигураций ионов хрома, таких как Cr³⁺(d³) и Cr²⁺(d⁴). Основным состоянием иона Cr³⁺ является орбитально невырожденный терм ⁴A₂. При переносе электрона – носителя тока по многоэлектронным ⁴А₂–состояниям образуются ионы Cr²⁺. Для хрома энергии термов ³Т₁(d⁴) и ⁵Е(d⁴) могут конкурировать между собой, что свидетельствует о возможном наличии в этом соединении двух типов донорных одночастичных возбуждений различной симметрии с энергиями ₁ = Е(³Т₁) – Е(⁴А₂) и ₂ = Е(⁵Е) – Е(⁴А₂). Одновременное существование разновалентных конфигураций d-ионов при выполнении условий энергетической близости dⁿ⁺¹ и dⁿ состояний может приводить к ряду уникальных физических свойств. Например, могут иметь место существенные отклонения от закона Блоха (Т^3/2) в температурном поведении намагниченности М(Т). В рамках спин-волновой теории ферромагнетиков с промежуточной валентностью выражение для намагниченности имеет вид:

M(T) = M₀ (1 – T – T^3/2Z_3/2(2_BH/kT)), (7)

где _В – магнетон Бора, k – постоянная Больцмана, Z_3/2– дзета-функция Римана для спина S = 3/2. Появление линейного по температуре слагаемого в формуле (7) обусловлено линейной температурной зависимостью химпотенциала .. В нормальном металле концентрация зонных электронов не зависит от температуры, поэтому зависимость (Т) слабая

(Т)  Т²/ <<  (8)

и происходит только из-за размытия фермиевской ступеньки. В системе с промежуточной валентностью только полная концентрация электронов не зависит от Т, а относительное число зонных и локализованных носителей заряда является функцией температуры. Температурная зависимость концентрации зонных электронов приводит к более сильной, чем в нормальном металле зависимости химпотенциала. В частности, появляется линейное слагаемое.

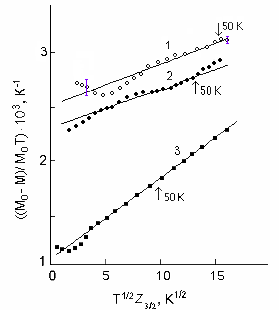
Температурные зависимости намагниченности n-HgCr₂Se₄ приведены на рис. 8(а). Математическая обработка экспериментальных данных показала, что в изменении намагниченности М с температурой отчетливо выделяются два различных вклада: блоховский М_3/2  Т^3/2 и линейный М₁  Т. Насколько удовлетворительна аппроксимация экспериментальных данных выражением (7), наглядно видно из рис. 8(б), где температурная зависимость намагниченности представлена в приведенных координатах (М₀ – М(Т))/М₀Т и Т^1/2Z_3/2(Н, Т). В этих координатах зависимость (7) имеет вид прямой линии, тангенс угла наклона которой равен величине , а отрезок, отсекаемый на оси ординат, дает значение .


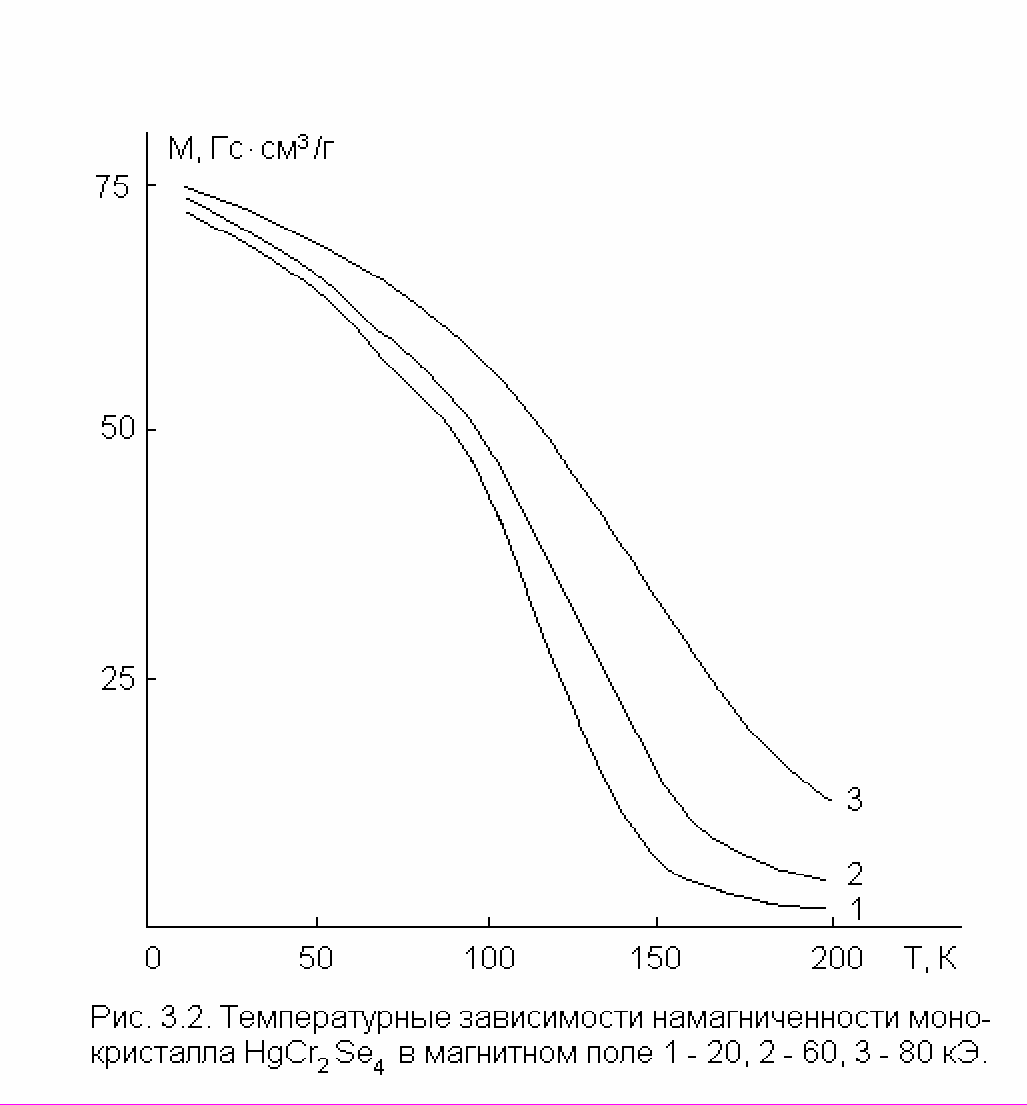
Рис. 8. Температурные зависимости намагниченности HgCr₂Se₄ в стандартных (слева) и приведенных (справа) координатах. Напряженность магнитного поля Н равна (1) – 20, (2) – 60, (3) 80 кЭ.

Все исследованные образцы ртутной шпинели демонстрировали монотонную температурную зависимость сопротивления R(T), причем при изменении температуры от комнатной до 4.2 К сопротивление уменьшалось приблизительно на два порядка. Холловская концентрация в наших образцах n  10¹⁸ см^-3, подвижность при комнатной температуре   10÷20 см²/Вс.

Одним из ярких эффектов, наблюдаемых в магнитном полупроводнике HgCr₂Se₄, является значительное магнитосопротивление, достигающее максимальной величины в окрестности температуры Кюри.

Для вырожденных магнитных полупроводников характерна слабая зависимость концентрации носителей от температуры в широкой области температур. Следовательно, изменения в проводимости можно отнести на счет изменяющейся с температурой подвижности носителей заряда. Ни один известный механизм рассеяния носителей заряда не воспроизводит экспериментально наблюдаемую зависимость подвижности. Кроме того, увеличение подвижности на два порядка до величин, характерных для широкозонных полупро-водников, свидетельствует в пользу значительных изменений с температурой самой зонной структуры полупроводника.

В случае кристаллов n-типа узкая зона, образованная d-состояниями, является частично заполненной донорными электронами, и по ней возможен перенос носителей с малой подвижностью при Т > Т_С. Понижение дна зоны проводимости вследствие раздвижки спиновых подзон при магнитном упорядочения приводит к сближению энергий d-уровня  и зоны проводимости. В этом случае твердотельная конфигурация может быть записана в виде d^n+s^q- , и d-ионы приобретают дробную валентность. В результате плотность состояний на d-уровне уменьшается, а в его окрестности значительно возрастает, что приводит к соответствующему увеличению электронной подвижности. Благодаря сложной структуре дна зоны проводимости состояние электрона на уровне Ферми имеет вероятностный характер. С некоторой вероятностью u² электрон может находиться в s-подобном, а с вероятностью v²=1–u² в d-подобном состоянии. Величину u² можно вычислить по формуле [3]:

u² =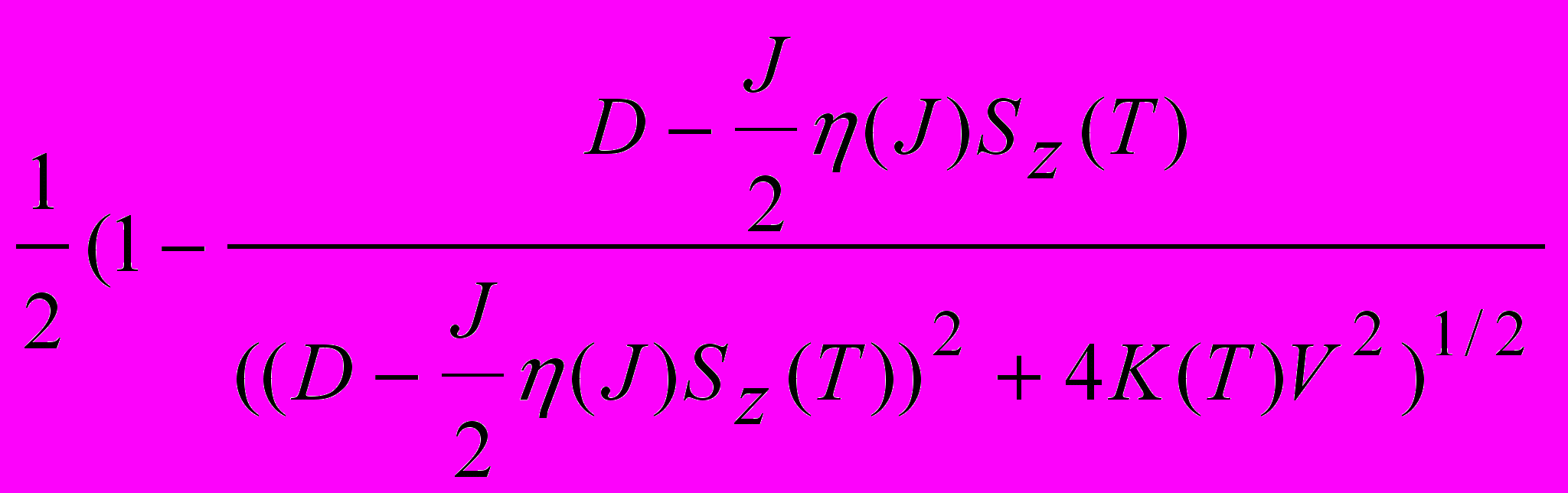) , (9)

где D = E_C –  – глубина залегания резонансного уровня относительно дна зоны проводимости Е_С; S_Z – спин магнитного иона; K = ¼(5/2 + (0)S_Z) – коэффициент, характеризующий температурную зависимость плотности состояний квазичастиц Cr³⁺ + e^-  Cr²⁺ (S = 2) и их эффективную гибридизацию с s-состояниями; (J) = sign (J).

Учет обменного взаимодействия s- и d-электронов приводит к температурной и магнитополевой зависимостям вероятностей распределения электронов по состояниям.

Если предположить, что электрон в s-подобном состоянии обладает определенным временем релаксации _s >> _d, ясно, что эффективное время релаксации будет возрастать с уменьшением температуры вместе с долей s-подобных состояний. Поскольку эффективная скорость релаксации является аддитивной величиной, выражение для эффективной подвижности электронов  можно записать в виде:

1/ = , (10)

где _s и _d – подвижности электрона в s- и d-состояниях. Смысл коэффициентов u² и v² заключается в вероятностях, с которыми носитель участвует в рассеянии на соответствующем потенциале s- и d-состояний.

П
Рис. 9. Зависимость относительной подвижности от температуры Т (слева) и спина Sz магнитного иона (справа). Точки – эксперимент, сплошная линия – расчет при J = 0.8, V = 0.4 и D = 0.25 эВ.



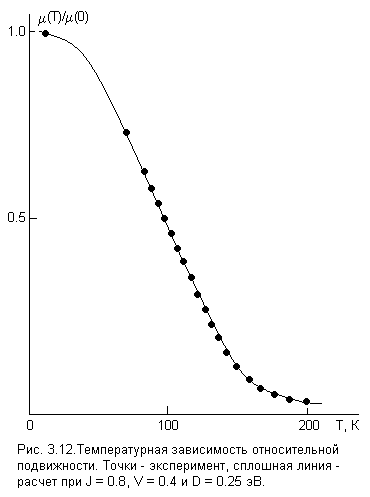
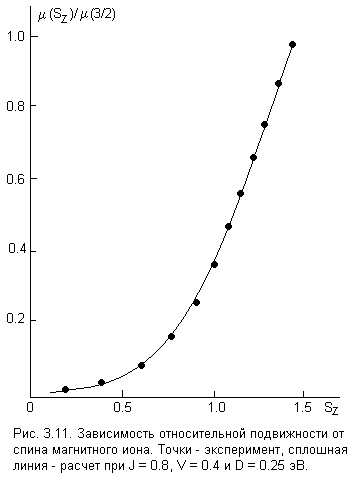
ри низких температурах s-зона диффузных состояний под действием sd-обменного взаимодействия опускается ниже –уровня, поэтому доля носителей в s-состояниях велика: u² 1 и   _s. С повышением температуры действие обменного взаимодействия на s- зону слабеет, т.к. S_z  0, приводя к ее превышению над –уровнем. При этом носители переходят в бестоковые d-состояния, а их доля в s-состояниях u²  0. Следовательно, в парафазе при Т >> Т_С   _d. Отсюда 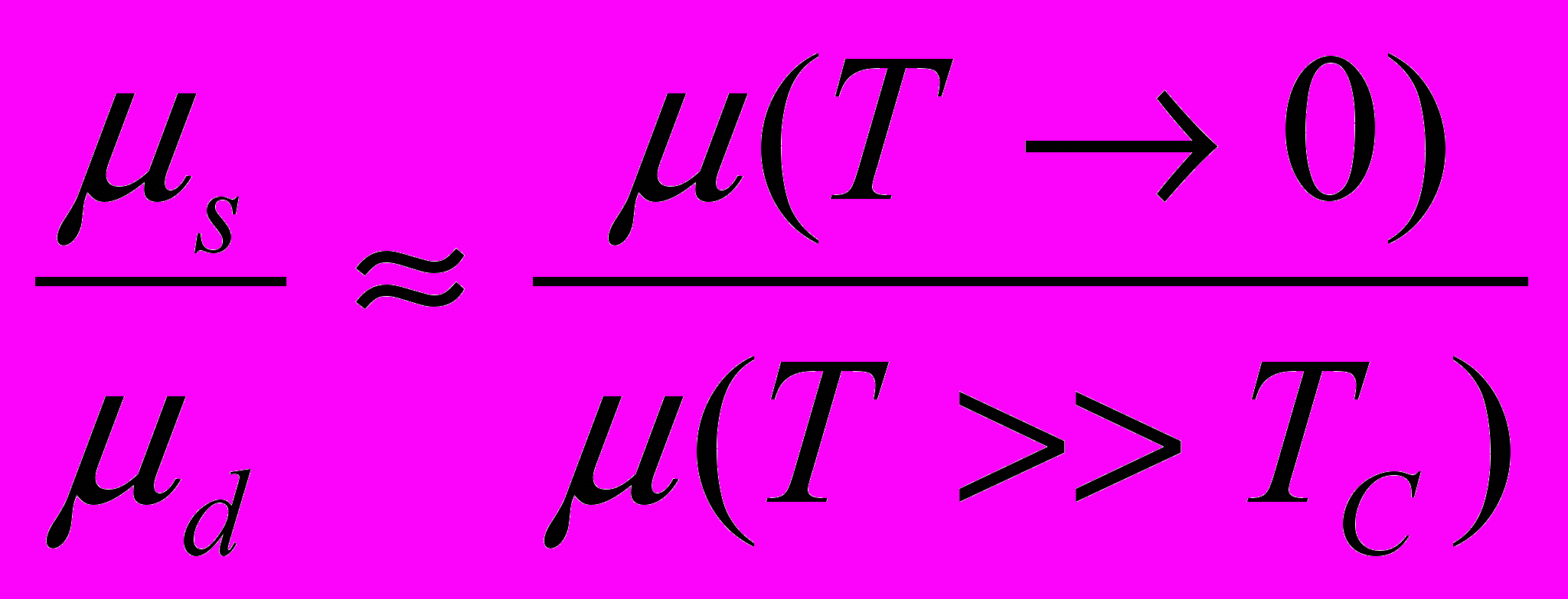. Аппроксимация экспериментальных данных выражениями (9) и (10) дает очень хорошее совпадение эксперимента и модельных представлений и позволяет оценить значения параметров J, V и D. Наилучшее совпадение экспериментальной и теоретической зависимостей было получено при J = 0.8 эВ, V = 0.4 эВ и D = 0.25 эВ, что отражено на рис. 9. Полученные значения параметров указывают на то, что зона проводимости в парамагнитной фазе уже является частично гибридизованной, что и обеспечивает вырождение электронного газа и достаточно высокую подвижность при Т = 300 К..

При анализе магнитополевых зависимостей намагниченности монокристалла n-HgCr₂Se₄ выяснилось, что при низких температурах в зависимости М(Н) наблюдается осциллирующий вклад (рис. 10). Этот эффект привлекает особое внимание, поскольку ранее он не наблюдался в других родственных магнитных полупроводниках. Амплитуды осцилляций невелики, однако они превышают погрешность измерений.

Р
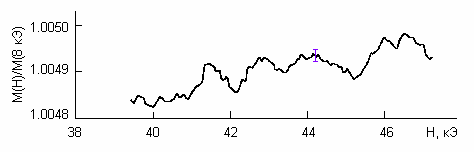
ис. 10. Магнитополевая зависимость относительной намагниченности HgCr₂Se₄ при Т = 4.2 К.

Наличие осциллируещей компоненты в намагниченности может быть связано с проявлением эффекта де Гааза - ван Альфена (дГвА), основанном на квантовании электронных орбит в магнитном поле. Как правило, такое квантование приводит к периодическим по 1/Н осцилляциям термодинамических и кинетических характеристик вырожденных Ферми-систем. Если зависимости химического потенциала  от температуры и магнитного поля отличаются от стандартных ферми-жидкостных, то возможны аномальные квантовые осцилляции. Осцилляции намагниченности, наблюдаемые нами в n-HgCr₂Se₄ слабопериодичны по 1/Н. Фурье-обработка намагниченности в интервале магнитных полей 8–20 кЭ дает размытый пик спектральной плотности сигнала, соответствующий примерному значению периода по 1/Н в 0.8  10^-6 Э. Тогда экстремальное сечение поверхности Ферми S = 9.3  10¹³ см^-2. При этом концентрация носителей n  4.3  10¹⁸ cм^-3, что хорошо согласуется с данными холловских измерений.

Теория эффекта дГвА в ферромагнетиках с промежуточной валентностью построена в [5]. Согласно выводам этой работы, фаза осциллирующей части намагниченности зависит от магнитного поля как  = a/H + b/H, (11)

где а и b – не зависящие от поля константы. В результате периодичность по 1/Н пропадает, хотя сама возможность осцилляций за счет пересечения уровня Ферми и уровней Ландау сохраняется.

П
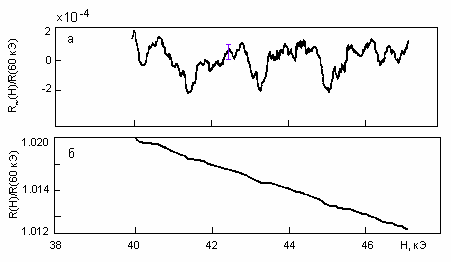
оскольку поведение электросопротивления n-HgCr₂Se₄ обусловлено изменениями электронной структуры, которая изменяется вслед за намагниченностью, квантовые осцилляции должны также проявиться и в

Рис. 11. Внизу – магнитополевая зависимость полного сопротивления,

вверху – магнитополевая зависимость его осциллирующей части.

электропроводности образцов. В действительности, при температуре Т = 4.2 К в магнитополевой зависимости электросопротивления наблюдается слабопериодичный осциллирующий вклад R_ (рис. 11).

Осциллирующая часть сопротивления наложена на линейное по полю магнитосопротивление, поэтому зависимость R(H) можно представить в виде R(H) = R_(H) – cH. (12)

Экспериментальные зависимости дают значение параметра с = R(60 кЭ) 10^-4 кЭ^-1. Сравнение графиков, приведенных на рис. 10 и 11 дает наложение экстремумов в осциллирующей части намагниченности и сопротивления. Таким образом, наряду с эффектом дГвА в магнитном полупроводнике HgCr₂Se₄ может наблюдаться также и эффект Шубникова–де Гааза, однако полевая зависимость обоих эффектов не описывается традиционными для ферми-жидкости функциями периодическими по 1/H.

Очень сильная взаимосвязь магнитной электронной подсистем имеет место и в другом классе соединений с сильно коррелированными электронами – ВТСП купратах. Соединение La₂CuO₄ является родоначальником этого класса материалов. В данной работе изучены особенности формирования взаимосвязи магнитных и электрических свойств специально недопированного монокристалла La₂CuO₄. В основном состоянии это соединение антиферромагнитно с Т_N  300 К. Дла нашего образца Т_N = 240 К, что указывает на нестехиометрию по кислороду и на наличие избыточных дырок. Такую же температуру Нееля имеет соединение La_1,99Sr_0.01CuO₄.

Недопированный La₂CuO₄ является диэлектриком. Природа диэлектрического состояния в La₂CuO₄ определяется сильными электронными корреляциями. Зонная структура квазичастиц и спектральная плотность сильно зависят от температуры в антиферромагнитной фазе, природа этой зависимости обусловлена перераспределением спектрального веса между различными квазичастицами с изменением температуры. Эти зависимости не могут быть получены в традиционном одноэлектронном подходе и являются следствием специфики зонной структуры квазичастиц в сильно коррелированнных электронных системах.

На рис. 12 приведена температурная зависимость сопротивления La₂CuO₄. Сопротивление измерено в направлении тетрагональной оси перпендикулярно плоскости CuО. В окрестности точки Нееля наблюдается аномалия, соответствующая примерно двукратному увеличению сопротивления.


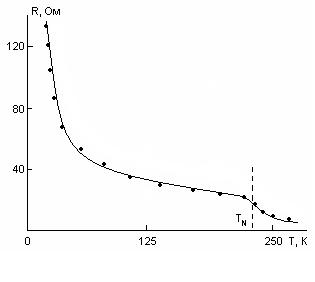
Рис. 12. Температурная зави-симость электросопротивления La₂CuO₄.
Расчеты зонной структуры La₂CuO₄ в рамках обобщенного метода сильной связи, явно включающего сильные электронные корреляции, показали, что электронная структура этого соединения достаточно сложна, и не может быть представлена простой схемой как на рис. 1 и 6 для хромовых шпинелей и боратов. Валентная зона La₂CuO₄ представляет собой набор большого числа узких зон. В [6] показано, что в антиферромагнитной фазе зона проводимости сужается, щель растет, но в данном соединении этот эффект слабый. Сильнее изменяется картина плотности состояний вблизи краев щели. При переходе в магнитоупорядоченное состояние пик в плотности состояний на дне пустой зоны проводимости сужается, и его интенсивность растет, а пик вблизи потолка валентной зоны ослабевает. Изменение структуры краев зон при магнитном упорядочении соответствует изменению спектральной плотности квазичастиц, участвующих в процессах переноса, и изменению их подвижности аналогично n-HgCr₂Se₄.

Увеличение сопротивления в два раза при переходе из парамагнитного в антиферромагнитное состояние позволяет оценить отношение эффективных подвижностей в антиферромагнитной и парамагнитной фазах:  _АФ / _ПМ = ½. Тогда изменение вероятностей u² и v² при изменении магнитного состояния: u²_АФ = 2u²_ПМ – 1. Проведенные в [6] расчеты параметров электронного спектра La₂CuO₄ в рамках многоэлектронной модели дают значение u²_ПМ = 0.85. Тогда u²_АФ = 0.7, что означает уменьшение доли sp-подобных состояний примерно на 15%.

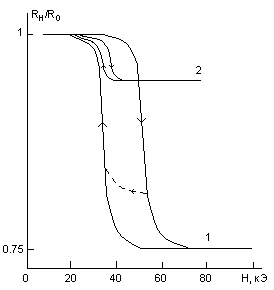
Влияние магнитного состояния La₂CuO₄ на транспортные свойства очень ярко проявляется при сравнении полевых зависимостей намагниченности и магнитосопротивления. Магнитополевые зависимости намагниченности, полученные в магнитном поле, направленном вдоль оси с кристалла, приведены на рис. 13. Кривые обладают ярко выраженным гистерезисом. Гистерезис также наблюдается и на магнитополевых зависимостях относительного сопротивления монокристалла La₂CuO₄ (рис. 13). Как и в случае намагниченности, ширина петли возрастает с понижением температуры. Отличие приводимых здесь результатов от полученных ранее заключается в том, что измерения полевых зависимостей сопротивления и намагниченности выполнены с одинаковой скоростью, что позволило сопоставить скачок в сопротивлении магнитному переориентационному переходу.

В узкозонных магнитных полупроводниках при переходе из однородной ферромагнитной фазы в антиферромагнитную имеет место спин-поляронное сужение зоны и уменьшение подвижности носителей, поскольку в неоднородной магнитной структуре перескок носителей без переворота спина затруднен. В данном случае с ростом магнитного поля имеем обратный процесс – при переходе в фазу с однородной компонентой намагниченности увеличивается подвижность носителей и уменьшается сопротивление. Этот механизм отрицательного магнитосопротивления проявляется как при зонном характере носителей в узких зонах, так и при прыжковом механизме в п
олупроводниках с глубокими примесными состояниями малого радиуса.



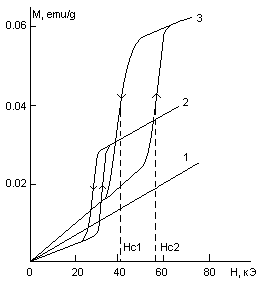
Рис. 13. Магнитополевые зависимости намагниченности М(Н) La₂CuO₄ при температурах 1 – 240 К, 2 – 160 К, 3 – 4.2 К (слева). Магнитополевые зависимости сопротивления La₂CuO₄ при температурах 1– 40, 2 – 115 К (справа).

В настоящее время рассмотренные особенности взаимосвязи электрических и магнитных свойств допированного дырками La₂CuO₄ хорошо известны [7]. Результаты, описываемые в данной работе, были получены в 1990 году, как только стали доступны качественные монокристаллы La₂CuO₄. В то время было опубликовано лишь несколько работ с описаниями свойств этого соединения.

Резюме к четвертой главе: в магнитном полупроводнике n-HgCr₂Se₄ и недопированном купрате La₂CuO₄ имеет место ярко выраженная взаимосвязь магнитных и электрических свойств. В обоих соединениях она формируется вследствие особенностей электронной структуры. В n-HgCr₂Se₄ в основе этой взаимосвязи лежит перемешивание коллективизированных и локализованных электронных состояний ввиду их энергетической близости и большого s-d обменного взаимодействия. В купратах La₂CuO₄ аномалия сопротивления в точке Нееля также связана с перестройкой электронной структуры при магнитном упорядочении.

В третьей и четвертой главах было рассмотрено взаимосвязанное поведение магнитного порядка и электронного транспорта на фоне изменений температуры и магнитного поля.