«Задача это необходимость сознательного поиска соответствующего средства для достижения некоторой цели»

Вид материала

Задача

Содержание Печатается по решению учебно-методического совета Ульяновского института повышения квалификации и переподготовки работников обра Решение задачи начинается с Основным методом По степени сложности физические задачи делятся на элементарные, стандартные и нестандартные. Решение задач на движение тела, брошенного вертикально вверх или вниз, или свободно падающее (здесь угол α = 90 Начало координат совмещаем с точкой, в которой находится тело В (рис. 3). Задача №3. Определить время качения шарика по плоскости ХОУ, которая наклонена к плоскости горизонта под углом β, если он пущен В этом случае составляющая скорости шарика V На электрон в электрическом поле действует сила A - архимедова сила, T - сила натяжения нити и F А и В имеют скорости V Спортсмены бегут от тренера со скоростью (v – u), поэтому первый спортсмен за время t убежит на расстояние L При последовательном соединении конденсаторов их общая электроёмкость определяется по формуле Построения изображения предмета при двух положениях линзы приведены на рис. 17 а) и б). Здесь d Электроны, вылетающие под действием света из катода, обладают кинетической энергией, если энергия фотона больше работы выхода эл Пусть первый шарик массой m в самый последний момент до удара со вторым шариком массой 3m имеет импульс Сначала определим скорость V При подключении резистора с сопротивлением R к источнику тока с ЭДС Согласно уравнению Эйнштейна для фотоэффекта Она показывает, какое количество теплоты Q необходимо для повышения температуры одного моля газа на единицу. Единицей измерения ... Полное содержание

Подобный материал:

• 1 Постановки экстремальных задач, 55.69kb.
• Агрессивное поведение, 293.27kb.
• Методы поиска идей и создания инноваций, 1291.23kb.
• Принятие решений составная часть любой управленческой функции. Необходимость принятия, 344.17kb.
• В. В. Климов национальный исследовательский ядерный университет «мифи» модели, методы, 10.26kb.
• 1 Сеть мип – это совокупность учреждений, имеющих общие цели, ресурсы для их достижения, 89.75kb.
• Задачи задачи для достижения Цели 1 Задачи для достижения Цели, 316.99kb.
• Анализ учебно воспитательной работы гоу сош №499 за 2009-2010учебный год, 2632.6kb.
• Это совокупность связанных элементов, объединенных в одно целое для достижения определенной, 235.02kb.
• Система хранения коллекций информационных ресурсов, предназначенная для хранения, обработки,, 33.84kb.

Ульяновский институт повышения квалификации

и переподготовки работников образования


Кафедра физико-математического образования


Кудрявцев Ю.Н.


МЕТОДЫ РЕШЕНИЯ
ФИЗИЧЕСКИХ ЗАДАЧ





Ульяновск

2010


Методы решения физических задач / Ю.Н. Кудрявцев. – Ульяновск:

УИПКПРО, 2010 – 43 с.


Учебно-методическое пособие предназначено для учителей физики, работающих в старших классах средних общеобразовательных учреждениях и готовящих учащихся к ЕГЭ. Здесь описаны основные методы, использующиеся при решении многих физических задач. Каждый из методов рассмотрен на примерах решения конкретных физических задач.


Печатается по решению учебно-методического совета Ульяновского института повышения квалификации и переподготовки работников образования.


Ульяновский институт повышения квалификации и переподготовки

работников образования, 2010

Ю.Н. Кудрявцев, 2010


Введение.


«Задача – это необходимость сознательного поиска соответствующего

средства для достижения некоторой цели».

Д. Пойа.


Физическая задача - это проблема, решаемая с помощью логических умозаключений, математических действий на основе законов и методов физики. Решение физических задач относится к практическим методам обучения и, опираясь на активную мыслительную деятельность ученика, выполняет образовательную, воспитательную и развивающую функции. Физический смысл различных определений, правил, законов становится понятным учащимся лишь после многократного применения их к конкретным частным примерам – задачам. Воспитательная функция физических задач заключается в формировании научного мировоззрения учащихся. Решение задач воспитывает трудолюбие, самостоятельность в суждениях, интерес к учению, упорство в достижении поставленной цели. При решении задач развиваются логическое и творческое мышление.

Общая структура деятельности по решению задачи.




Решение задачи начинается с анализа условия. Ученик должен не только запомнить условие, но и осознать его, увидев физическое явление, о котором говорится в задаче. На этапе поиска решения ученик вспоминает физические законы, определения, описывающие рассматриваемое в задаче физическое явление, строит его математическую модель.

Основным методом поиска решения задачи является аналитико-синтетический способ. Аналитические рассуждения направлены от искомых задачи к её данным. Анализ требует разделения целого на части. При синтезе двигаются в рассуждениях от данных задачи к искомым. Синтез объединяет отдельные элементы в целое.

На этапе решения производятся преобразования записанных формул, осуществляется намеченный план решения. Здесь проявляется математическая подготовка учащихся.

Проверка результата заключается в определении достоверности числового значения искомой величины или её размерности при отсутствии числовых данных.

Исследование решения является очень важным этапом, имеющим большие дидактические возможности, позволяющим глубже проанализировать физическое явление. Никакую задачу нельзя исчерпать до конца, поскольку всегда остаётся что-то, над чем можно поразмышлять, найти другое решение задачи.

По степени сложности физические задачи делятся на элементарные, стандартные и нестандартные.

Для решения элементарной задачи необходимо и достаточно воспроизвести и применить один соответствующий физический закон. Решение стандартной задачи требует системы обычных знаний и стандартных методов и приёмов. Нестандартная задача требует особых методов решения, поскольку применение обычных законов и методов не приводит к цели, так как система уравнений получается незамкнутой. Как правило, нестандартные задачи встречаются в олимпиадных заданиях. В распространённых сборниках задач по физике приводятся стандартные задачи.

Методике обучения учащихся решению задач посвящено значительное количество работ учёных, методистов, учителей – практиков [1, 2, 3, 4. 5]. Однако затруднения в решении задач по-прежнему остаются наиболее частыми затруднениями, которые испытывают учащиеся школ, особенно при решении задач части С заданий ЕГЭ.

Анализ программ по физике, поурочного планирования учебного материала показывает, что о задачах говорится только в разделе «Требования к знаниям и умениям учащихся». Примерное поурочное планирование учебного материала предлагает примерно 20% учебного времени отводить на уроки по решению задач. Остальное время отводится на формирование у учащихся знаний о физических понятиях, законах, принципах, теориях, экспериментах. Возникает противоречие: большая часть времени уделяется изучению теоретического материала, а на контрольных работах проверяется умение решать задачи, чему практически не учат. Создаётся впечатление, что умение решать задачи является само собой разумеющимся, если знать теорию вопроса. Однако это умение не может возникнуть само собой, оно требует специального обучения.

По мнению авторов [1, 2, 3] главная причина неумения решать задачи состоит в том, что учащихся не учат методам решения, которые для отдельных классов задач выражаются в виде алгоритмов или предписаний алгоритмического типа. Метод - (от греч. methodos - путь исследования), способ достижения какой-либо цели, решения конкретной задачи; совокупность приемов или операций практического или теоретического освоения (познания) действительности.

Целью данного пособия является обзор методов решения задач, которыми должен владеть учитель физики, чтобы помочь учащимся подготовиться к итоговой аттестации в виде заданий ЕГЭ. Условия некоторых задач заимствованы из работ [ 6,7,8] и КИМ-ов ЕГЭ.


§1. Координатный метод решения задач.


Этот метод широко используется при решении задач по механике во всех её разделах: кинематике, динамике, статике.

1.1. Решение кинематических задач координатным методом.

Основной задачей кинематики является составление уравнений координат тела (материальной точки) как функции времени. В школьном курсе физики это уравнение вида

Х = Х₀ + V_0х t + а_х t²/ 2. (1.1)


Здесь Х₀ - начальная координата материальной точки, V_0x – проекция вектора начальной скорости на ось ОХ, а_x– проекция вектора ускорения на ось ОХ.


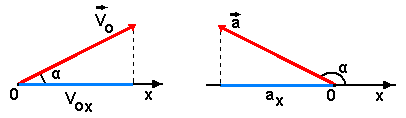
Проекцией вектора на ось называют скалярную величину, равную произведению модуля вектора на косинус угла, который этот вектор образует с положительным направлением оси. В зависимости от угла α проекция вектора может быть положительной при 0^о ≤ α < 90^о _, равной нулю при α = 90^о, отрицательной при 90^о < α ≤ 180^о. На рис. 1,а показано определение проекции вектора начальной скорости V_oх на ось ОХ, на рис. 1,б – проекции вектора ускорения а_х.





а) б)

Рис. 1


а) V_0x = V₀ cos α ; б) a_x = а cos (180^o – α ) = ­­- a cos α. (1.2)

Проекция вектора скорости положительна, а проекция вектора ускорения – отрицательна. Знак проекции вектора определяется знаком косинуса угла α.

Из уравнения (1.1) можно получить уравнение для проекции на ось Х вектора скорости как функции времени путём дифференцирования (1.1) по времени.

V_х = dx/dt = V_0х + а_хt. (1.3)

Умение составлять уравнения (1.1) и (1.3) и является одним из главных умений, необходимых для решения кинематических задач.

Наиболее общей задачей на движение тела в поле силы тяжести (гравитационном поле) является задача о движении тела, брошенного под углом к горизонту.


Задача №1. Девочка бросает мяч с балкона, находящегося на высоте h от поверхности земли, под углом α к горизонту со скоростью V₀. Определить время полета мяча до земли, дальность полёта (координату X_max точки падения), наибольшую высоту полёта мяча над землёй (максимальное значение координаты У_max мяча) и скорость мяча в момент его падения на землю.


Р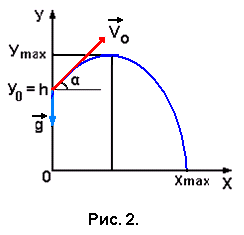ешение задачи начинается с выбора начала отсчёта, с которым совмещают начало координат ХОУ, рационально направив оси координат. В данном случае удобно начало отсчета и связанное с ним начало координат выбрать на поверхности земли под балконом, направив оси Х и У соответственно горизонтально и вертикально. Отмечаем на оси У начальную координату мяча У₀ = h, направляем вектор начальной скорости V₀ под углом α к горизонту и изображаем траекторию полёта мяча, которая, как известно, представляет собой параболу. Точка пересечения параболы с осью Х определит координату X_max , значение которой даст дальность полёта мяча. Наибольшая высота полёта мяча определится значением координаты У_max вершины параболы. Рисунок к задаче будет иметь вид (рис.2). Для составления уравнений движения Х = Х(t) и У = У(t) вида (1.1) имеет смысл записать составляющие этих уравнений:




Х₀ = 0;

V_0x = V₀ cos α X = ( V₀ cos α) t (1.4)

g_x = 0;


У₀ = h;

V_0y = V₀ cos (90^{o –} α) =

V₀ sinα; У = h +V₀ sinα)– gt²/2 (1.5)

g_y = - g;

Далее начинается аналитическая работа с уравнениями (1.4) и (1.5). Через время t_п (время полёта мяча) координаты мяча примут значения: Х = Х_max, у = 0. Тогда уравнения (1.4) и (1.5) примут вид:

Х_max = V₀(cosα)t_п; (1.6)

0 = h + ( V₀ sinα) t_п– gt_п²/ 2. (1.7)

Решая квадратное уравнение (1.7), находим время полёта мяча t_п.

t _п = [ V₀ sin α + (V₀² sin²α + 2gh)^1/2]/g , (1.8)

которое имеет только одно значение. Второе - отрицательное значение t_п, которое следует из решения квадратного уравнения, не возможно. Здесь и далее корень квадратный из числа записывается как это число в степени ½.

Подставив значение t_п в уравнение (1.6), определяем дальность полёта мяча Х_max.

Х_max = V₀(cosα) = V₀(cosα) [ V₀ sin α + (V₀² sin²α + 2gh)^1/2]/g. (1.9)

В верхней точке траектории мяча высота его полёта максимальна, а проекция скорости на ось ОУ равна нулю. Для продолжения решения необходимо перейти к уравнениям проекций скорости V на оси Х и У как функциям времени. Взяв производные по времени от (1.4) и (1.5), получаем:

V_x = V₀ cos α; (1.10)

V_y = V₀ sinα - gt. (1.11)

Уравнение (1.10) показывает, что вдоль оси ОХ мяч летит равномерно с постоянной скоростью, не зависящей от времени. Движение мяча вдоль оси ОУ является равнопеременным (при движении до верхней точки полёта – равнозамедленным, а затем становится равноускоренным). В момент времени t_в (время полёта мяча до верхней точки) проекция скорости V_y становится равной нулю, а координата У принимает максимальное значение у_max.

0 = V₀ sinα - gt_в; (1.12)

у_max = h + ( V₀ sinα) t_в– gt_в²/ 2. (1.13)

Определив из уравнения (1.12) время t_в,

t_в = (V₀ sinα) / g, (1.14)

подставляем его значение в уравнение (1.13) и определяем у_max- максимальную высоту полёта мяча.

у_max = h + ( V₀² sin²α) / 2g. (1.15)

Для определения скорости мяча в момент падения (время t_п) необходимо определить значения проекций этой скорости V_x и V_y в этот момент.

V_x определяем из уравнения (1.10), V_y из уравнения (1.11), подставив в него значение t_п:

V_y = V₀sinα - gt_п = V₀ sinα - g [ V₀ sin α + (V₀² sin²α + 2gh)^1/2]/g (1.16) ,

Скорость мяча в момент падения V определится по теореме Пифагора:

V = (V_x² + V_y²)^1/2. (1.17)

Проекция V_y будет отрицательной, но будучи возведённой в квадрат даст положительное значение. Следует помнить, что вектор скорости в любой точке направлен по касательной к траектории движения.


Решение задач на движение тела, брошенного вертикально вверх или вниз, или свободно падающее (здесь угол α = 90^о) сводится к составлению только одного уравнения:

У = h + V₀ t – gt²/2. (1.18)

Уравнение (1.18) записано для случая бросания тела вертикально вверх с высоты h. Ось У направлена вверх, начало координат совпадает с уровнем земли.

Если тело брошено горизонтально (α = 0^о), то уравнения движения (1.4) и (1.5) принимают вид:

Х = V₀ t; (1.19)

У = h – gt²/ 2. (1.20)

Если в задаче описывается движение двух тел, то нужно составлять уравнения движения для каждого тела. Если в какой-то момент времени одно тело догоняет другое или они встречаются (сталкиваются), то это означает, что в этот момент времени они приобретают одинаковые координаты Х и У.




Задача №2. Тело А свободно падает с высоты h, тело В, находящееся на расстоянии L от предполагаемой точки падения тела А, бросают так, чтобы оно в полёте столкнулось с телом А. Под каким углом α к горизонту нужно бросить тело В и с какой скоростью, чтобы столкновение было возможным.

Начало координат совмещаем с точкой, в которой находится тело В (рис. 3).

Записываем уравнения движения тел.

Для тела А: Х_А = L; (1.21)

У_А = Н - gt²/ 2. (1.22)

Для тела В:

Х_в = ( V₀ cos α) t; (1.23)

У_в = ( V₀ sinα) t – gt²/2. (1.24)


При столкновении Х_А = Х_в; У_А = У_в, приравняв правые части (1.21) и (1.23), а также (1.22) и (1.24) получим уравнения:

L = ( V₀ cos α) t; (1.25)

Н - gt²/ 2 = ( V₀ sinα) t – gt²/2 или Н = ( V₀ sinα) t. (1.26)

Разделив (1.26) на (1.25), получим соотношение

H / L = sinα / cos α = tg α, откуда α = arc tg H/L. (1.27)

Выражение (1.27) показывает, что вектор V₀ скорости тела В должен быть направлен точно в точку, где в начальный момент находится тело А. Только в этом случае возможно столкновение тел А и В.

Минимальная величина этой скорости должна быть такой, чтобы тело В за время падения тела А с высоты Н смогло пролететь по оси Х расстояние равное L, в этом случае столкновение тел произойдёт в точке падения тела А. Уравнения движения тел примут вид:

для тела А: 0 = Н – gt _п²/ 2; (1.28)

для тела В: L = ( V₀ cos α) t_п. (1.29)

Здесь t_п – время свободного падения тела А. Решив систему уравнений (1.28) и (1.29) относительно V₀ , получим выражение

V₀ = [g (H² + L²) / 2H]^1/2 (1.30)

При всех начальных скоростях тела В больших значения, определяемого соотношением (1.30), столкновение тел А и В происходит обязательно, и чем больше значение V₀, тем координата У точки столкновения будет больше, конечно, если вектор начальной скорости направлен под углом к горизонту, определяемым соотношением (1.27).


Задача №3. Определить время качения шарика по плоскости ХОУ, которая наклонена к плоскости горизонта под углом β, если он пущен под углом α к оси ОХ со скоростью V₀ (рис. 4). Трением шарика о поверхность пренебречь.


В этом случае составляющая скорости шарика V_0У будет меняться за счёт действия составляющей ускорения g_У, которая равна

g_У = g sinβ. (1.31)

Тогда уравнение координаты У примет вид:

У = V_0У t - g_У t²/2 = (V₀sinα)t - (g sinβ)t²/2. (1.32)

Качение шарика по плоскости завершится в момент времени t_k, когда он пересечёт ось ОХ в точке с координатой Х =Х_max.

В этот момент координата У шарика станет равной нулю и уравнение (1.32) примет вид:

(V₀sinα)t_k - (g sinβ)t²_k/2 = 0, (1.33)

откуда время качения

t_k = 2 (V₀sinα) / (g sinβ). (1.34)

Как видно из (1.34) время качения шарика при одинаковых начальных скоростях V₀ будет тем больше, чем меньше угол β наклона плоскости ХОУ к

горизонтальной плоскости.


Задача № 4. Шарик, падая вертикально, отскакивает от абсолютно твёрдой наклонной плоскости, расположенной под углом α к горизонту, со скоростью V₀. Определить на каком расстоянии от точки падения шарик снова упадёт на наклонную плоскость.

При абсолютно упругом ударе шарика о наклонную плоскость угол отскока α от наклонной плоскости равен углу падения шарика на наклонную плоскость, т.к. составляющая скорости вдоль наклонной плоскости остаётся постоянной, а составляющая перпендикулярная наклонной плоскости меняет направление на противоположное, сохраняя свою величину. В данной задаче удобно направить оси координат так, как показано

на рис. 5 (ось ОХ вдоль наклонной плоско-

сти, ось ОУ - перпендикулярно ей).

Уравнения движения шарика вдоль координатных осей будут иметь следующий вид:

Х = ( V₀ sin α) t + (g sin α) t² / 2; (1.35)

У = ( V₀ cos α) t –(g cos α) t² / 2. (1.36)

При t равном времени полёта t_п Х = Х_max, а У = 0. Тогда уравнения (1.35) и (1.36) принимают вид:

Х_max= ( V₀ sin α) t_п+ (g sin α) t_п² / 2; (1.37)

0 = ( V₀ cos α) t_п–(g cos α) t_п² / 2. (1.38)

Из (1.38) определим время полёта

t_п = 2V₀/g. (1.39)

Шарик упадёт на наклонную плоскость на расстоянии от точки падения равном

Х_max = 4 V₀² sin α / g. (1.40)


Координатный метод используется при решении задач о движении заряженных частиц в электрическом однородном поле. В этом случае необходимо определить величину и направление вектора ускорения, сообщаемого электрическим полем заряженной частице, а затем составить уравнения движения.


Задача № 5. Электрон влетает в область однородного электрического поля напряжённости 200 В/м со скоростью 10⁷м/с. Определить, на каком расстоянии от места входа в поле электрон выйдет из него, если он влетает под углом 45^ок направлению поля.




На электрон в электрическом поле действует сила F = eE. Здесь Е – вектор напряжённости электрического поля, е – заряд электрона. Так как заряд электрона отрицательный, то сила направлена против направления силовых линий электрического поля или против направления вектора напряжённости. Эта сила вызывает ускорение

а = F/m = Ee/m, (1.41)

которое, как и сила, направлено против электрического поля (рис. 6). Направив ось ОХ вертикально, а ось ОУ горизонтально, получаем ситуацию равносильную движению материальной точки, брошенной под углом к горизонту в поле тяготения Земли.

Уравнения движения электрона будут иметь вид:

Х = (V_o sin α) t; (1.42)

У = (V_o cos α)t – at²/2. (1.43)

Электрон покинет область поля в точке, имеющей координаты Х = Х_max и У = 0. Определим время пребывания t _п электрона в электрическом поле из уравнения:

0 = (V_o cos α)t_п – at_п²/2; t _п = (2V_o cos α)/a = (2mV_o cos α)/Ee. (1.44)


Тогда Х_max = (2m V_o² sin α cos α)/Ee = (m V_o² sin 2α)/Ee, (1.45)

Подставив значения физических величин, данных в задаче (V_o,Е,α) и заимствованных из таблицы фундаментальных физических постоянных (е, m) получаем Х_max = 2,8 м.


Задача № 6. Протон и α-частица, двигаясь с одинаковой скоростью, влетают в плоский конденсатор параллельно пластинам. Во сколько раз отклонение протона полем конденсатора от прямолинейной траектории будет больше отклонения α-частицы?


Электрическое поле конденсатора считается однородным. Силовые линии такого поля перпендикулярны пластинам конденсатора и параллельны друг другу. Напряжённость поля Е является постоянной величиной. Поскольку протон и α – частица имеют положительный заряд, то сила, действующая на них со стороны электрического поля, направлена по направлению вектора напряжённости Е поля. Такое же направление будет иметь вектор ускорения а, вызванного действием этой силы (рис. 7). Ось ОХ направим параллельно пластинам конденсатора, ось ОУ – перпендикулярно пластинам вверх. Запишем уравнения движения заряженных частиц в этом поле:

Х = V_o t ; (1.46)

У = at²/2. (1.47)

Время пролёта частиц сквозь область электрического поля определится из соотношения t_п = L/V_o, (1.48)

где L – длина пластин конденсатора.

Отклонение от прямолинейной траектории частиц

У_max = at _п²/2 = а L²/2V_o². (1.49)

Ускорение, получаемое частицей в электрическом поле, определяется также как и в предыдущей задаче,

a = q E / m. (1.50)

Подставив (1.50) в (1.49), получаем

У_max = q E L²/ 2 m V_o² . (1.51)

Заряд α – частицы в 2 раза больше заряда протона, а её масса в 4 раза больше массы протона. Отношение отклонений частиц электрическим полем конденсатора определится соотношением

У_{р max} / У_{α max} = q_p m_α / q_α m_p = 2. (1.52)

1.2. Решение задач по динамике координатным методом.

Координатный метод находит применение и при решении задач по динамике. Здесь используются понятия проекций вектора силы и ускорения на координатную ось. Основное уравнение динамики или второй закон Ньютона, записанный в форме проекций сил и ускорения на координатную ось ОХ, выглядит так: Σ F_ix = ma_x. Умение составлять такие уравнения является основой для решения динамических задач, в которых, как правило, требуется определить ускорение в движении тела или системы тел и пассивные силы (силы трения, натяжения связывающих тела нитей, реакций опор).




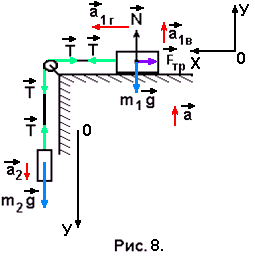
Задача № 7. Cистема из двух грузов массами m₁ и m₂ (рис. 8) находится в лифте. движущемся вверх с ускорением а. Найти силу натяжения Т нити, если коэффициент трения между грузом m₁ и опорой равен μ.


Грузы связаны нерастяжимой нитью, поэтому ускорения грузов относительно стола одинаковы по величине и равны а'. В неподвижной системе отсчёта ускорение груза m₂ направлено по вертикали и равно а₂ = а' – а. Ускорение груза m₁ имеет две составляющие: вертикальную а_1в = а и горизонтальную а_1г = а'.

Запишем второй закон Ньютона для движения каждого из грузов в виде проекций сил и ускорений на координатные оси:

для первого груза массой m₁ ОХ: Т – F_тр = m₁a_1г;

ОУ: N - m₁g = m₁a_1в; F_тр = μ N или

Т – μ N = m₁а';

N – m₁g = m₁a; (1.53)

для второго груза массой m₂

ОУ: m₂g – T = m₂a₂ или

m₂g – T = m₂ (а' – а). (1.54)

Решая полученную систему, состоящую из двух уравнений (1.53) и уравнения (1.54), получаем выражение для силы натяжения нити

Т = m₁m₂ (g + a)(1 + μ) / (m₁ + m₂). (1.55)


Задача № 8. К вершине прямого кругового конуса прикреплена небольшая шайба с помощью нити длиной L = 1 м. Вся система вращается вокруг оси конуса, расположенной вертикально. Каков угол при вершине конуса 2φ, если при минимальном числе оборотов шайбы n = 0,7 с ^-1 её давление на боковую поверхность конуса становится равным нулю?


При вращении шайбы по боковой поверхности конуса на неё действуют следующие силы: mg – сила тяжести, Т – сила натяжения нити, N – сила реакции поверхности конуса. В сумме они создают равнодействующую силу, которая сообщает шайбе центростремительное ускорение (рис. 9). Ось ОХ направляем вдоль вектора а_цс в его направлении, ось ОУ – вертикально. Тогда уравнения динамики в проекциях на оси ОХ и ОУ будут иметь вид:

ОХ: Т sin φ – N cos φ = ma_цс; (1.56)

Рис. 9. ОУ: Т cos φ + N sin φ – mg = 0. (1.57)

Пока шайба не оторвалась от поверхности конуса, сила реакции N > 0. В момент отрыва и после отрыва от поверхности

N = 0. Центростремительное ускорение a_цс = v²/R , где R – радиус окружности, которую описывает шайба при движении по поверхности конуса. R = L sin φ. Линейная скорость v связана с числом оборотов в секунду n соотношением:

v = 2πRn. Учитывая всё это, запишем уравнения (1.56) и (1.57) в виде:

Т = m 4π²n² L; (1.58)

Т cos φ = mg. (1.59)

Разделив (1.59) на (1.58), получим соотношение:

cos φ = g/ 4π²n² L. (1.60)

Подставив в (1.60) числовые значения n и L, определим угол 2φ при вершине конуса: cos φ = 9,8 / 4 ^. 3,14^{2 .} 0,7^{2 .} 1 = 0,5, следовательно, φ = 60^о, а 2φ = 120^о.


1.3. Применение координатного метода к статическим задачам.

Координатный метод широко используется при решении статических задач. Если тело находится в равновесии под действием сходящейся системы сил, линии действия которых пересекаются в одной точке, то условие равновесия записывается в виде следующих соотношений: Σ F_ix = 0 и Σ F_iy =0 для плоской системы сходящихся сил, вектора которых лежат в одной плоскости. Если система сходящихся сил является пространственной, то к выше приведённым уравнениям добавляется уравнение Σ F_iz = 0.


З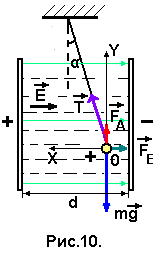адача № 9. Заряженный алюминиевый шарик радиуса r, подвешенный на тонкой нерастяжимой нити, находится между двумя параллельными вертикальными пластинами, расстояние между которыми d. Пространство между пластинами заполнено керосином. Каков заряд шарика, если при подаче на пластины напряжения U угол отклонения нити равен α?


Изобразим шарик в положении равновесия, в котором нить образует угол α с вертикалью. Электрическое поле, возникающее между пластинами при подаче на них напряжения U, считаем однородным. Силовые линии такого поля параллельны друг другу и направлены перпендикулярно поверхностям пластин от пластины с большим потенциалом (+) к пластине с меньшим потенциалом (-). Вектор напряжённости Е параллелен силовым линиям, а его величина определяется соотношением: Е = U/εd,

где ε – диэлектрическая проницаемость керосина.

На шарик действуют силы: mg - сила тяжести, F _A - архимедова сила, T - сила натяжения нити и F_E - сила, действующая на заряд шарика со стороны электрического поля (рис. 10).

Запишем условия равновесия шарика в виде проекций сил на координатные оси

ОХ: Тsin α – F_E = 0; (1.61)

OY: Tcos α + F_A – mg = 0. (1.62)

Представим эти уравнения в виде:

Т sin α = F_E;

Tcos α = mg - F_A.

Поделив левые и правые части этих уравнений, получим соотношение

tg α = F_E / (mg – F_A). (1.63)

Из этого уравнения выразим силу F_E

F_E = (mg – F_A) tg α. (1.64)

По законам электростатики эта сила определяется по формуле:

F_E = E q = U q / ε d, (1.65)

где q - заряд шарика.

Приравняв правые части (1.64) и (1.65) получим уравнение, из которого можно найти заряд шарика:

U q / ε d = (mg – F_A) tg α. (1.66)

Подставим в уравнение (1.66) выражения для силы тяжести и силы Архимеда, связав их с плотностями алюминия и керосина, соответственно:

mg = ρ_a Vg = (4/3) π r³ ρ_ag, (1.67)

F_A = ρ_k Vg = (4/3) π r³ ρ_kg. (1.68)

Получим уравнение

U q / ε d = (4/3) π r³g (ρ_a - ρ_k) tg α, (1.69)

из которого найдём заряд шарика

q = 4π r³g ε d (ρ_a - ρ_k) tg α / 3U. (1.70)


В случае произвольной (несходящейся) плоской системы сил, кроме равенства нулю сумм проекций сил на координатные оси ОХ и ОУ требуется равенство нулю суммы моментов сил относительно оси, перпендикулярной плоскости чертежа и проходящей через произвольную точку.

Моментом силы относительно оси называют скалярную величину, определяемую произведением модуля силы на плечо силы. Плечом силы называют кратчайшее расстояние между осью вращения и линией действия силы. Если под действием силы тело вращается вокруг оси против направления движения часовой стрелки, то момент такой силы считается положительным, если по часовой – отрицательным.


Задача № 10. Лестница массой m прислонена к стене. Чему равен минимальный угол φ между лестницей и полом, при котором лестница ещё находится в равновесии, если коэффициент трения между лестницей и стеной равен μ₁, а между лестницей и полом μ₂? Определить силы реакции стены и пола, а также силы трения между лестницей и полом, лестницей и стеной.


Лестницу считаем телом однородным по всей длине, поэтому С - точка приложения силы тяжести mg лежит в середине лестницы АВ (рис. 11). На лестницу в точке А действуют сила трения F_ТР1 и сила реакции стены N₁, в точке В – сила трения F_ТР2 и сила реакции пола N₂ (рис. 11).

В данном случае имеет место плоская, произвольная система сил, поэтому условие равновесия лестницы будет представлено в виде трёх уравнений: равных нулю сумм проекций на координатные оси всех сил системы и равной нулю суммы моментов относительно оси, проходящей через точку А или В перпендикулярно плоскости чертежа. Выбор этих осей обусловлен тем, что в первом случае (точка А) «выбывают из игры» силы F_ТР1 и N₁, а во втором случае (точка В) – силы F_ТР2 и N₂, поскольку в этих случаях эти силы не имеют плеч и их моменты становятся равными нулю.

ОХ: N₁ - F_ТР2 = 0; (1.56)

ОУ: F_ТР1 + N₂ – mg = 0; (1.57)

Рис. 11. В качестве моментной точки выберем точку В, тогда сумма моментов относительно оси, проходящей через эту точку, предстанет в виде: F_ТР1 L cos φ + N₁ L sin φ - (mgL/2) cos φ = 0. (1.58)

В этом случае моменты сил F_ТР2 и N₂ равны нулю, так как равны нулю их плечи. Следует учесть, что F_ТР1 = μ₁N₁, а F_ТР2 = μ₂N₂, тогда уравнения (1.56) -(1.58) примут вид: N₁ - μ₂N₂ = 0;

μ₁N₁ + N₂ – mg = 0;

μ₁N₁ cos φ + N₁ sin φ - (mg/2) cos φ = 0. (1.59)

Из первых двух уравнений определим силы реакций стенки и пола

N₁ = μ₂ mg/ (1 + μ₁ μ₂); N₂ = mg/ (1 + μ₁ μ₂).

Разделив уравнение (1.59) на cos φ, получим уравнение, из которого определим минимальный угол наклона лестницы.

μ₁N₁ + N₁ tg φ - (mg/2) = 0. (1.60)

Подставив в (1.60) выражение для N₁ и сократив на mg, получим уравнение, из которого определим тангенс угла наклона лестницы и сам угол наклона:

tg φ = (1 – μ₁μ₂) / 2μ₂; φ = arc tg φ[(1 – μ₁μ₂) / 2μ₂].

Силы трения стенки N₁ и пола N₂ равны, соответственно:

F_ТР1 = μ₁ μ₂ mg/ (1 + μ₁ μ₂); F_ТР2 = μ₂ mg/ (1 + μ₁ μ₂).