«Задача это необходимость сознательного поиска соответствующего средства для достижения некоторой цели»

Вид материала

Задача

Содержание При решении задачи используем соотношение между изменением скорости и пройденным путём Вакуумный насос – это устройство, которое при работе создаёт в объёме своей рабочей камеры ΔV пониженное давление (порядка 10 Поскольку все грузы связаны между собой, то они движутся с одинаковым ускорением. Запишем уравнения движения для каждого груза в Эквивалентное сопротивление цепи равно сопротивлению четырёх резисторов, соединённых между собой в цепь, изображённую на рис. 42 Разделим узел О на две точки, получив два варианта электрической цепи (рис. 45, а) и (рис. 45, б). В первом случае потенциалы то Рассмотрим преобразование схем, имеющих три вывода (трёхполюсников). В «звезде» сопротивление между точками 1 и 2 равно r

Подобный материал:

• 1 Постановки экстремальных задач, 55.69kb.
• Агрессивное поведение, 293.27kb.
• Методы поиска идей и создания инноваций, 1291.23kb.
• Принятие решений составная часть любой управленческой функции. Необходимость принятия, 344.17kb.
• В. В. Климов национальный исследовательский ядерный университет «мифи» модели, методы, 10.26kb.
• 1 Сеть мип – это совокупность учреждений, имеющих общие цели, ресурсы для их достижения, 89.75kb.
• Задачи задачи для достижения Цели 1 Задачи для достижения Цели, 316.99kb.
• Анализ учебно воспитательной работы гоу сош №499 за 2009-2010учебный год, 2632.6kb.
• Это совокупность связанных элементов, объединенных в одно целое для достижения определенной, 235.02kb.
• Система хранения коллекций информационных ресурсов, предназначенная для хранения, обработки,, 33.84kb.

§6. Метод отрицательных масс.


Этот метод используется при решении задач на определение положения центра масс фигуры, имеющей удалённые из неё участки. В этом случае массу удалённого участка считают отрицательной, а силу тяжести этого участка (-mg) направляют вверх. В дальнейшем используют условие равновесия тела, находящегося под действием системы параллельных сил. Здесь используется понятие момента силы.


Задача №31. Определить координату Х_С центра масс однородного цилиндра радиуса R, в котором высверлено сквозное цилиндрическое отверстие радиуса r, ось которого параллельна оси цилиндра и находится от неё на расстоянии d.

Изобразим поперечное сечение цилиндра с высверленным в нём цилиндрическим отверстием. Сечение проводим через середину длины цилиндра. Центр масс (точка С) (рис. 31) находится на оси Х, проходящей через т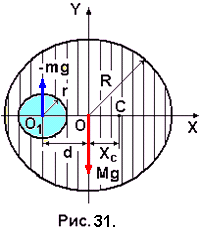очки О и О₁. После удаления цилиндрической части радиуса r он смещается вправо от оси основного цилиндра. На рисунке указываем силы тяжестей сплошного цилиндра Mg и удалённого цилиндра (-mg). Под действием этих сил цилиндр остаётся в равновесии, если ось вращения проходит через центр масс. Условие равновесия тела, имеющего ось вращения заключается в равенстве нулю суммы моментов сил, приложенных к телу, относительно этой оси. Условие равновесия в нашем случае будет иметь вид:

Mg X_C - mg(d + X_C) = 0. (6.1)

Массы М и m определим по формулам:

М = ρ V = ρ πR²L; m = ρ π r²L, (6.2)

где ρ – плотность материала цилиндра, L – длина цилиндра.

После подстановки (6.2) в (6.1) и преобразований получаем выражение:

R² X_C - r²(d – X_C) = 0, (6.3)

Откуда получаем значение координаты центра масс Х_С:

Х_С = d [r²/ (R² + r²)]. (6.4)


Задача № 32. Определить координату центра масс алюминиевого цилиндра радиуса R, в котором сквозное высверленное цилиндрическое отверстие радиуса r залито свинцом. Расстояние между осями алюминиевого цилиндра и заполненного отверстия d.


Поскольку плотность свинца больше плотности алюминия, то центр масс (точка С) такого цилиндра сместится влево от оси основного цилиндра. Масса высверленного алюминиевого цилиндра m₁ считается отрицательной, поэтому сила тяжести (-m₁g) направлена вверх, а сила тяжести заполняющего это отверстие свинца m₂g направлена, как обычно, вниз (рис. 32). Массы М, m₁ и m₂ определим по формулам:

М = ρ_Al πR²L; m₁ = ρ_Al πr²L; m₂ = ρ_Pb πr²L. (6.5)

Уравнение равновесия цилиндра относительно оси, проходящей через центр масс, будет иметь вид:

m₂g(d – X_C) - m₁g (d – X_C ) - Mg X_C = 0. (6.6)

После подстановки значений М, m₁ и m₂ из (6.5) в (6.6) и преобразований получим выражение, определяющее координату центра масс данного цилиндра:

X_C = dr² ( ρ_Pb - ρ_Al)/[ ρ_Al(R²- r ²) + ρ_Pbr ²]. (6.7)


§ 7. Метод индукции.


Этот метод подобен методу математической индукции, с помощью которого устанавливается общая зависимость некоторых величин по их частным зависимостям.


Задача № 33. Гоночный автомобиль («болид») движется равноускоренно из состояния покоя. На первых десяти метрах его скорость возрастает на 10 м/с. Определить возрастание его скорости на тех же десяти метрах при прохождении от 990-го метра до 1000-го метра пути и сравнить с возрастанием на первых десяти метрах. Дать объяснение их значительному расхождению.


При решении задачи используем соотношение между изменением скорости и пройденным путём:

V² - V₀² = 2aS. (7.1)

Скорость автомобиля после прохождения первого десятиметрового отрезка ( S = 10 м) определится соотношением:

V₁² = V₀² + 2aS = 0 + 2aS = 2aS; ( 7.2)

после прохождения второго:

V₂² = V₁² + 2aS = 2aS +2aS = 4aS = 2V₁²; ( 7.3)

после прохождения третьего:

V₃² = V₂² + 2aS = 4aS + 2aS = 6aS = 3V₁² ; ( 7.4)

Следовательно, между обеими частями равенств (7.2) - (7.4) просматривается зависимость вида:

V_n² = n V₁², ( 7.5)

откуда связь между скоростью при прохождении n-го десятиметрового отрезка и первого выразится соотношением:

V_n = (n)^1/2 V₁ . (7.6)

Используя соотношение (7.6) определим скорость после прохождения

99 -го и 100 -го десятиметровых отрезков, соответственно,

V₉₉ = (99)^1/2 V₁, V₁₀₀ = (100)^1/2 V₁; (7.7)

тогда возрастание скорости на десятиметровом отрезке между 990 м и 1000 м пути составит:

Δ V_{(99 – 100)} = [(100)^1/2 – (99)^1/2] V₁ ≈ 0,5 (м/с). (7.8)

На первых десяти метрах скорость возросла на 10 м/с, а на сотом таком отрезке пути всего на 0,5 м/с. Это потому, что при прохождении сотого отрезка длиной в 10 м скорость автомобиля составляет около 100 м/с (360 км/ч), и «болид» проскакивает эти десять метров за очень малый промежуток времени, в течение которого и скорость увеличивается незначительно. Так как при равноускоренном движении ΔV = a Δt, то время проскакивания «болидом» этих десяти метров составит Δt = ΔV_{(99 – 100)} /a.

Ускорение можно определить из уравнения (7.2)

а = V₁²/ 2S = 10²/ (2 ^.10) = 5 м/с²,

тогда Δt = 0,5 м/с / 5 м/с² = 0,1 с.


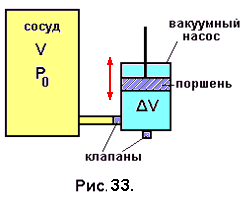
Задача №34. Поршневым вакуумным насосом ( рис. 33) с рабочей камерой объёмом ΔV откачивают воздух из сосуда объёмом V от давления P₀ до давления Р_n (P_n< P₀). Определить число n ходов поршня, которое должно быть совершено при этом. Процесс откачки считать изотермическим.


Вакуумный насос – это устройство, которое при работе создаёт в объёме своей рабочей камеры ΔV пониженное давление (порядка 10 ^-3 – 10^-4 мм рт. ст.) Поэтому при подключении насоса к откачиваемому объёму общий объём становится равным V + ΔV, газ расширяется, заполняя оба объёма, и понижает своё давление. Тот газ, который заполняет рабочую камеру насоса, отсекается насосом и выталкивается в атмосферу. «Пустой» объём рабочей камеры вновь подключается к откачиваемому объёму. Происходит очередное расширение газа, приводящее к очередному понижению давления, и т. д. Так как процесс считается изотермическим, то, используя закон Бойля – Мариотта, можно для начального состояния газа в откачиваемом объёме и состояния газа после первого подключения рабочей камеры насоса записать уравнение:

Р₀V=P₁(V+ΔV), (7.9)

из которого определим давление в сосуде после первого хода поршня насоса

Р₁ = Р₀V / (V + ΔV ). (7.10)

Тогда после второго подключения можно записать уравнение:

Р₁ V = P₂ (V + ΔV ), (7.11)

откуда определим давление в сосуде после второго хода поршня насоса:

Р₂ = Р₁V / (V + ΔV ) = Р₀ [V / (V + ΔV )]². (7.12)

Аналогично для третьего хода поршня вакуумного насоса:

Р₂ V = P₃ (V + ΔV ),

P₃ = Р₂ V / (V + ΔV ) = Р₀ [V / (V + ΔV )]³. (7.13)

Из анализа уравнений (7.10), (7.12) и (7.13) просматривается зависимость, связывающая давление в сосуде после n-го хода поршня P_n c первоначальным давлением Р₀:

P_n = Р₀ [V / (V + ΔV )]ⁿ. (7.14)

Для нахождения числа ходов поршня n логарифмируем уравнение (7.14):

lg P_n = lg P₀ + n lg [V / (V + ΔV )], (7.15)

откуда

n = lg (P_n/ P₀) / lg [V / (V + ΔV )]. (7.16)

При достижении в откачиваемом объёме давления равного давлению в рабочей камере насоса (10 ^-3 – 10 ^-4 мм рт.ст.) процесс откачки прекращается и насос лишь поддерживает достигнутый вакуум.


Задача №35. На рис. 34 изображена система связанных грузов одинаковой массы m. Определить ускорение, с которым движется система, и силы натяжения нитей, связывающих грузы. Трением между горизонтальной поверхностью и грузами, расположенными на ней, пренебречь.


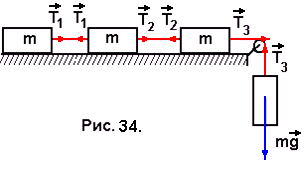Поскольку все грузы связаны между собой, то они движутся с одинаковым ускорением. Запишем уравнения движения для каждого груза в отдельности:

mg – T₃ = ma;

T₃ - T₂ = ma; (7.17)

T₂ - T₁ = ma;

T₁ = ma.

Сложив левые и правые части равенств системы четырёх уравнений (7.17), получим уравнение:

mg = 4 ma, откуда a = g / 4 . (7.18)


Теперь определим силы натяжения нитей:

T₁ = ma = mg / 4;

T₂ = T₁ + ma = 2 mg / 4; (7.19)

T₃ = T₂ + ma = 3 mg / 4.

Анализируя уравнения (7.18) и (7.19), можно записать уравнения для ускорения и сил натяжения нитей в случае системы, состоящей из n одинаковых грузов, приводимой в движение силой тяжести одного из них.

a = g / n; T_k = k (mg / n), (7.20)

где n – общее число грузов, составляющих связанную систему, k – число грузов, которое приводит в движение k -ая сила натяжения.


§ 8. Методы расчёта резисторных схем постоянного тока.

8.1. Расчёт эквивалентных сопротивлений линейных бесконечных цепей.


Линейные бесконечные цепи, как правило, симметричны и во многих случаях содержат одинаковые повторяющиеся элементы, состоящие из резисторов. Расчёт сводится к определению эквивалентного сопротивления, равного сопротивлению всей цепи.


Задача № 36. Найдите эквивалентное сопротивление бесконечной цепи (рис. 35), которая состоит из одинаковых резисторов сопротивлением R каждый.




Для определения эквивалентного сопротивления цепи выделим общий элемент, который бесконечно повторяется. Очевидно, что если отделить его от цепи, то общее сопротивление цепи не изменится, т.к. число таких элементов бесконечно. Выделив повторяющийся элемент цепи и заменив сопротивление остальной цепи искомым сопротивлением R_X, получим э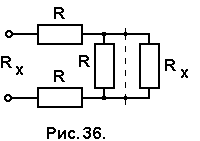квивалентную схему (рис. 36), сопротивление которой определим по формуле

R_X = 2R + RR_X/ ( R + R_X), (8.1)

или

R_X^{2 –} 2RR_X – 2R² = 0. (8.2)

Решив это квадратное уравнение, получаем значение эквивалентного сопротивления

R_X = R (1 + 3^1/2). (8.3)


Задача № 37. Найдите эквивалентное сопротивление бесконечной цепи

(рис. 37,а), которая состоит из одинаковых резисторов сопротивлением R каждый.

Применим такой же приём, но с другим повторяющимся элементом цепи (рис. 37,б).

R_X = (2R + R_X)R/[(2R + R_X) + R] = (2R + R_X)R/(3R + R_X)

или

R_X² + 2RR_X – 2R² = 0. (8.4)

Решив это квадратное уравнение, получим значение эквивалентного сопротивления данной бесконечной цепи:

R_X = R (3^1/2 - 1). (8.5)


З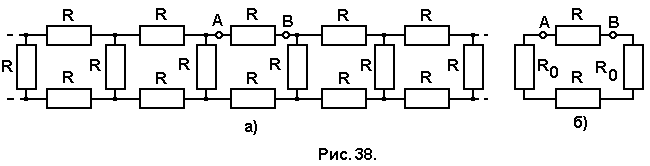адача № 38. Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки (рис. 38,а) которая состоит из одинаковых резисторов сопротивлением R каждый.

Эквивалентное сопротивление цепи равно сопротивлению четырёх резисторов, соединённых между собой в цепь, изображённую на рис. 42.

Сопротивления R₀ одинаковы и равны R₀ = R (3^1/2 - 1) (8.6)

(смотри решение задачи № 37).

Тогда эквивалентное сопротивление между точками А и В будет равно:

R_AB = (2R₀ + R)R/ (2R₀ + R) + R. (8.7)

Подставив значение R₀ из (8.4) и произведя преобразования, получим

R_AB = R(6 – 3^1/2)/6.


8.2. Шаговый (рекуррентный) метод расчёта эквивалентного сопротивления электрической цепи.


Данный метод удобен в том случае, когда схема представляет собой некоторое число повторяющихся структурных элементов. Этот метод основан на том, что результат первого действия (шага) используется во втором, второй – в третьем и т.д. Число шагов зависит от числа повторяющихся структурных элементов.


Задача № 39. Найти сопротивление цепи, изображённой на рис. 39.




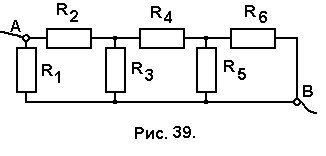
Для решения задачи изобразим схему цепи в более удобном для расчётов и наглядном виде (рис.40,а). Теперь видно, что цепь представляет собой три вложенных друг в друга групп резисторов, соединённых параллельно. Начинают пошаговое определение эквивалентных сопротивлений с самых внутренних элементов. Заменим резисторы R₄ , R₅ , R₆ резистором R^’, величину которого определим по формуле: R^’ = R₄ + R₅ R₆ / (R₅ + R₆) (8.8)

В результате замены получим новую схему цепи (рис. 40, б). Аналогично рассчитываем эквивалентное сопротивление резисторов R₂, R₃ и R^’:

R^’’ = R₂ + R^’ R₃ / (R^’ + R₃). (8.9)

В итоге получаем простую схему (рис. 40,в), позволяющую определить сопротивление всей цепи

R _общ = R^’’ R₁ / (R^’’ + R₁). (8.10)


Задача № 40. Найти сопротивление цепи АВ, изображённой на рис. 41.




Расчёт эквивалентного сопротивления цепи АВ начинаем слева. Эквивалентное сопротивление участка цепи АС равно R, т. к. здесь включены параллельно два одинаковых сопротивления 2R. Участок АС соединён последовательно с сопротивлением R. Сопротивление верхней ветви участка АD равно 2R. Т.к. эта ветвь параллельна сопротивлению 2R, то общее сопротивление участка цепи АD равно R. Участок цепи AD соединён последовательно с участком DB, сопротивление которого равно R, поэтому эквивалентное сопротивление верхней ветви цепи АВ равно 2R. Поскольку это сопротивление параллельно сопротивлению 2R нижней ветви цепи АВ, то общее сопротивление цепи АВ равно R.


8.3. Метод объединения равнопотенциальных узлов.


Этот метод позволяет упрощать схемы электрических цепей путём объединения узлов, имеющих равные потенциалы в один узел.


Задача № 41. Найти сопротивление цепи АВ, изображённой на рис. 42,а.



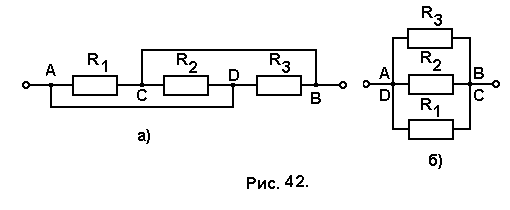
Так как сопротивление подводящих проводов считается равным нулю, то точки А и D, соединённые проводником имеют одинаковый потенциал, то же можно сказать и о потенциалах точек В и С. Объединив точки А и D в один узел и, сделав то же самое с точками В и С, получим простую схему из трёх параллельно соединённых резисторов (рис. 42,б). общее сопротивление цепи определим по формуле:

1/R_общ = 1/R₁ + 1/R₂ + 1/R₃, (8.11)

откуда

R_общ = R₁ R₂ R₃/( R₁R₂ + R₂R₃ + R₁R₃). (8.12)


Задача № 42. Найти сопротивление цепи, изображённой на рис.43,а, если сопротивления всех резисторов одинаковы и равны R.


Потенциалы точек 1 и 3 одинаковы, поэтому их можно объединить в одну, то же самое можно сделать с точками 2 и 5, 4 и 6. В результате получится видоизменённая упрощённая схема (рис. 43,б).

Резисторы R₁₂ и R₂₃ соединены параллельно, следовательно, их общее сопротивление равно R/2. Точно также общее сопротивление резисторов R₄₅ и R₅₆ равно R/2. Общее сопротивление части цепи параллельной R₃₄ равно R/2 + R/2 = R, поэтому сопротивление всей цепи будет равно R/2.


8.4. Метод разделения узлов.


Метод разделения узлов схемы основан на том, что, если возможно объединение двух узлов, имеющих равные потенциалы, то возможен и обратный переход: узел схемы можно разделить на две или несколько точек, если получившиеся при этом точки имеют прежние одинаковые потенциалы.


Задача № 43. Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис.44) сопротивлением R каждый.




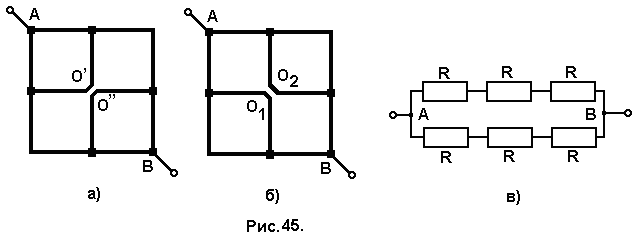Разделим узел О на две точки, получив два варианта электрической цепи (рис. 45, а) и (рис. 45, б). В первом случае потенциалы точек О^’ и О^’’ не равны. , Если потенциал точки А больше потенциала точки В, то потенциал точки О^’ больше потенциала точки О^’’ и наоборот. Потенциалы же точек О₁ и О₂ равны, так как находятся в одинаковых условиях (полностью симметричны). Отсюда следует, что верным является разделение узла О, показанное на рис. 45, б. Эквивалентная схема цепи, полученная после разделения узла О, изображена на рис. 45, в. Отсюда общее сопротивление цепи между точками А и В равно 3R/2.


Задача № 44. Найти сопротивление цепи, которая представляет собой каркас из одинаковых отрезков проволоки (рис. 46,а) сопротивлением R каждый.


Единственно верным способом разделения узла О на отдельные точки О₁, О₂ и О₃ является способ, изображённый на рис. 46,б. Эквивалентное сопротивление участков (cd) и (ef) будет равно

R_cd = R_ef = 2R R/ (2R + R) =2R/3. (8.13)

Эквивалентное сопротивление участка АО₁В равно 2R. Эквивалентная схема цепи, полученная после разделения узла О, изображена на рис. 46,в. Общее сопротивление цепи определим по формуле

1/ R_общ = 3/8R + 3/8R + 1/2R = 5/4R, (8.14)

откуда R_общ = 4R/5.


8.5. Метод преобразования и расчёта цепей с помощью перехода

«звезда» - «треугольник».


Этот метод основан на том, что схему, имеющую три узла, можно заменить другой, с тем же числом узлов. При этом сопротивление участка между двумя любыми узлами новой схемы должно быть равно сопротивлению заменяемого участка. В результате получается схема, сопротивление которой эквивалентно сопротивлению данной по условию. Поскольку в результате такого преобразования изменяются токи внутри цепи, то такую замену проводят в тех случаях, когда не нужно находить распределение токов.





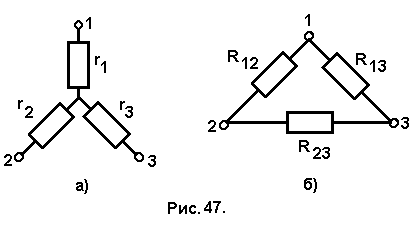
Рассмотрим преобразование схем, имеющих три вывода (трёхполюсников).

Это преобразование называется преобразованием «звезды» (рис. 47,а) в «треугольник» (рис. 47,б), и наоборот.

В «звезде» сопротивление между точками 1 и 2 равно r₁ + r₂, в «треугольнике» R₁₂ (R₁₃ + R₂₃)/(R₁₂ + R₁₃ + R₂₃). Следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо выполнение равенства:

r₁ + r₂ = R₁₂ (R₁₃ + R₂₃)/(R₁₂ + R₁₃ + R₂₃). (8.15)

Аналогично для точек 1 и 3 и для точек 2 и 3:

r₁ + r₃ = R₁₃ (R₁₂ + R₂₃)/(R₁₂ + R₁₃ + R₂₃). (8.16)

r₂ + r₃ = R₂₃ (R₁₂ + R₁₃)/(R₁₂ + R₁₃ + R₂₃). (8.17)

Сложив левые и правые части этих уравнений и разделив полученные суммы на 2, получим:

r₁ + r₂ + r₃ = (R₁₂ R₁₃ + R₁₂ R₂₃ + R₁₃ R₂₃)/ )/(R₁₂ + R₁₃ + R₂₃). (8.18)

Вычитая из (8.18) поочерёдно уравнения (8.17), (8.16) и (8.15), получим:

r₁ = R₁₂ R₁₃/ (R₁₂ + R₁₃ + R₂₃); (8.19)

r₂ = R₁₂ R₂₃/ (R₁₂ + R₁₃ + R₂₃); (8.20)

r₃ = R₁₃ R₂₃/ (R₁₂ + R₁₃ + R₂₃). (8.21)

Эти выражения легко запомнить: знаменатель в каждой формуле есть сумма сопротивлений всех резисторов «треугольника», а в числителе дважды повторяется индекс, стоящий слева: r₁ - R₁₂ R₁₃; r₂ - R₁₂ R₂₃; r₃ - R₁₃ R₂₃.

Аналогично получаются формулы для обратного преобразования:

R₁₂ = (r₁r₂ + r₁r₃ + r₂r₃) / r₃; (8.22)

R₁₃ = (r₁r₂ + r₁r₃ + r₂r₃) / r₂; (8.23)

R₂₃ = (r₁r₂ + r₁r₃ + r₂r₃) / r₁. (8.24)

Выражения (8.22) – (8.24) также легко запомнить: числитель у всех выражений один и тот же, а у сопротивления, стоящего в знаменателе, стоит тот индекс, которого не достаёт у сопротивления, стоящего в левой части выражения.

Задача № 45. Определите сопротивление цепи АВ (рис. 48.а), если R₁ = R₅ =

1 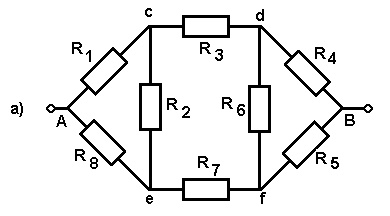Oм; R₂ = R₆ = 2 Oм; R₃ = R₇ =

3 Oм; R₄ = R₈ = 4 Oм.


Преобразуем «треугольники» R₁ R₂ R₈ R₄ R₅ R₆ в эквивалентные «звёзды», тогда схема примет вид, изображённый на рис. 48,б. Сопротивления r_1, r_2, r₃, … r₆ рассчитаем по формулам:


r₁ = R₁ R₈/ (R₁ + R₂ + R₈) = 4/7 Ом;




r₂ = R₁ R₂/ (R₁ + R₂ + R₈) = 2/7 Ом;


r₃ = R₂ R₈/ (R₁ + R₂ + R₈) = 8/7 Ом;


r₄ = R₄ R₆/ (R₄ + R₅ + R₆) = 8/7 Ом;


r₅ = R₅ R₆/ (R₄ + R₅ + R₆) = 2/7 Ом;

r₆ = R₄ R₅/ (R₄ + R₅ + R₆) = 4/7 Ом;

Схема, изображённая на рис. 48,в является эквивалентной схеме на рис. 48,б.

Здесь R’₃ = r₂ + R₃ + r₄ = 31/7 Ом;

R’₇ = r₃ + R₇ + r₅ = 31/7 Ом, R’₃ = R’₇.

Общее сопротивление цепи

R_общ = r₁ + R’₃/2 + r₆ = 47/14 Ом.


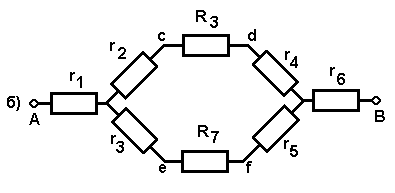
Задача № 46. Определить общее сопротивление неуравновешенного моста (рис. 49,а) , если R₁ = 1,0 Oм; R₂ = 1,6 Oм; R₃ = 2,0 Oм; R₄ = 1,2 Oм; R₅ = 2,0 Oм.




Если преобразовать «треугольник» из резисторов R₁, R₃, R₅ в эквивалентную «звезду», то получится простая схема (рис. 49,б). Рассчитаем сопротивления r₁, r₂ и r₃ по формулам: r₁ = R₁R₃/(R₁ + R₃ + R₅) = 0,4 Ом; r₂ = R₁R₅/(R₁ + R₃ + R₅) = 0,4 Ом; r₃ = R₃R₅/(R₁ + R₃ + R₅) = 0,8 Ом;

Общее сопротивление цепи R_общ = r₁ + (r₂ + R₂) (r₃ +R₄)/ (r₂ + R₂ + r₃ + R₄) = 1,4 Ом.