«Задача это необходимость сознательного поиска соответствующего средства для достижения некоторой цели»

Вид материала

Задача

Содержание Сторона АВ треугольника АВО связана со стороной ОВ соотношением A - архимедова сила, T - сила натяжения нити и F Модуль вектора Е определим по теореме косинусов, согласно которой Определим, с какой скоростью V Задания базового уровня Задания повышенного уровня Задания высокого уровня Примеры заданий базового уровня. Примеры решения задач в свёрнутом виде.

Подобный материал:

• 1 Постановки экстремальных задач, 55.69kb.
• Агрессивное поведение, 293.27kb.
• Методы поиска идей и создания инноваций, 1291.23kb.
• Принятие решений составная часть любой управленческой функции. Необходимость принятия, 344.17kb.
• В. В. Климов национальный исследовательский ядерный университет «мифи» модели, методы, 10.26kb.
• 1 Сеть мип – это совокупность учреждений, имеющих общие цели, ресурсы для их достижения, 89.75kb.
• Задачи задачи для достижения Цели 1 Задачи для достижения Цели, 316.99kb.
• Анализ учебно воспитательной работы гоу сош №499 за 2009-2010учебный год, 2632.6kb.
• Это совокупность связанных элементов, объединенных в одно целое для достижения определенной, 235.02kb.
• Система хранения коллекций информационных ресурсов, предназначенная для хранения, обработки,, 33.84kb.

§ 9. Векторный метод решения задач.


Этот метод используется в случае, если при сложении векторов получается замкнутый треугольник. Это может быть треугольник скоростей, сил, импульсов, напряжённостей электрических и индукций магнитных полей.


Задача № 47. Мальчик и девочка решили попасть из пункта А в пункт В, расположенные на противоположных берегах реки, скорость течения которой u. Мальчик плывёт так, чтобы сразу оказаться в пункте В. Девочка направляет скорость своего плавания поперёк скорости течения реки и, чтобы попасть в пункт В, должна пройти по противоположному берегу то расстояние, на которое её снесёт течением. С какой скоростью должна перемещаться девочка по берегу, чтобы оказаться в пункте В одновременно с мальчиком? Скорости и мальчика, и девочки относительно воды одинаковы и равны V.


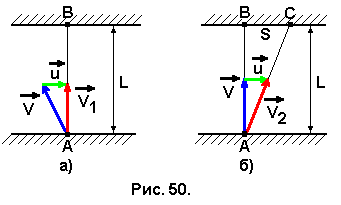
При решении используем закон сложения скоростей, согласно которому скорость тела относительно неподвижной системы отсчёта равна сумме скорости относительно подвижной системы и скорости самой подвижной системы. На рис. 50,а показана скорость мальчика V₁ относительно берегов, которая получается путём сложения скорости мальчика относительно воды V и скорости течения реки u. Модуль скорости V₁ определим по теореме Пифагора: V₁ = (V² – u²) ^1/2. (9.1)

Время, за которое мальчик сумеет переплыть реку по прямой АВ, определим по формуле: t₁ = L / V₁, (9.2)

где L – ширина реки.

На рис. 50,б показана скорость девочки V₂ относительно берегов реки, которая также равна сумме векторов скоростей девочки относительно воды V и течения реки u. Однако по модулю она равна

V₂ = (V² + u²)^1/2. (9.3)




Время, которое потребуется девочке, чтобы переплыть реку по прямой АС равно: t₂ = L / V, (9.4)

т.к. вдоль прямой АВ она плывёт со скоростью V. Поскольку V > V₁, то t₂ < t₁ на величину Δt = t₁ - t₂ = L (1/V₁ – 1/V). (9.5)

Девочка приплывает в пункт С и, чтобы попасть в пункт В вместе с мальчиком ей требуется перемещаться по прямой ВС со скоростью

V ^‘ = S/ Δt , (9.6)

где S – длина прямой ВС, представляющая собой расстояние, на которое сносит девочку течение реки. Из подобия векторного треугольника и треугольника АВС (рис. 50,б) составим пропорцию S/L = u/V, откуда найдём S:

S = Lu/V. (9.7)

Скорость перемещения девочки по прямой ВС будет равна:

V ^‘ = S/ Δt = Lu / VΔt ,

или после подстановки значения Δt из (9.5) и V₁ из (9.1):

V ^‘ = u / V(1/V₁ – 1/V) = u / V[1/(V² – u²) ^1/2 – 1/V]. (9.8)


Задача № 48. Однородный стержень массой 0,1 кг укреплён одним концом в шарнире и удерживается в равновесии с помощью нити, прикреплённой к другому её концу. Угол α между стержнем и вертикальным направлением равен 30^о. Найдите силы натяжения нити и реакции шарнира, если нить расположена горизонтально (рис. 51,а).


Сила реакции N шарнира, приложенная к стержню, не имеет вполне определённого направления, поэтому для его определения используем следующее положение: если стержень находится в равновесии под действием трёх сил, то система сил должна быть сходящейся. Следовательно, линия действия силы N должна проходить через точку D – точку пересечения линий действия сил mg и T, образуя угол β с вертикалью (рис. 51,а).

При равновесии силы должны образовать замкнутый прямоугольный треугольник (рис. 51,б). Угол β - угол между векторами N и mg, который нужно определить. Точка С- центр масс однородного стержня делит его длину пополам. Линия действия силы mg проходит через середину стержня параллельно вертикали ОВ, следовательно точка D, через которую она проходит, делит отрезок АВ пополам: AB = 2 BD. (9.9)

Сторона АВ треугольника АВО связана со стороной ОВ соотношением:

АВ = ОВ tgα. Сторона BD треугольника DВO связана с этой же стороной ОВ соотношением: BD = ОВ tg β.




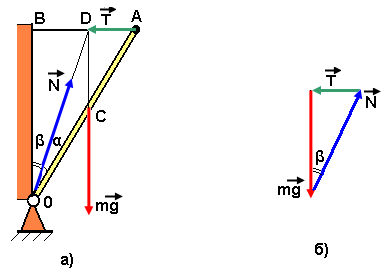
Рис. 51.


Подставив выражения для АВ и ВD в (9.9), получим соотношение:

tg α = 2 tg β, откуда tg β = (tg α)/2.

Из силового треугольника (рис. 51,б) сила натяжения нити определится так:

Т = mg tgβ = mg (tg α)/2; (9.10)

T = 0,1 ^. 9,8 ^. 0,5 ^. tg 30^o = 0,28 H.

Силу реакции шарнира N определим по теореме Пифагора:

N = [ T² + (mg)²]^1/2 (9.11)

N = [0,28² + (0,1 ^. 9,8)²]^1/2 = 1,02 H.


Задачу № 9 (стр.12) можно решить не только координатным методом, но и векторным.

На шарик действуют силы: mg - сила тяжести, F _A - архимедова сила, T - сила натяжения нити и F_E - сила, действующая на заряд шарика со стороны электрического поля (рис. 10).

Произведя сложение векторов этих сил, получим векторный треугольник со сторонами (mg – F_A), F_E и Т. По условию равновесия сумма векторов сил должна быть равна нулю, поэтому конец вектора Т должен совпасть с началом вектора mg (рис. 62). Так как сила натяжения направлена вдоль нити, а сила тяжести вертикально вниз, то между ними будет угол α . Угол между векторами mg и F_E прямой. Отношение противолежащего катета к прилежащему для угла α равно тангенсу этого угла:

tg α = F_E / (mg – F_A). (9.9)

Получаем уравнение идентичное уравнению (1.63)


Задача № 49. Два точечных заряда q₁ = + q и q₂ = - 2q расположены на расстоянии r друг от друга. Определить напряжённость электрического поля в точке, которая находится на расстоянии r₁ от первого заряда и на расстоянии r₂ от второго.


Напряжённость электрического поля, созданного точечным зарядом в точке, находящейся на расстоянии r от него, определяется по формуле:

Е = q/ 4πε₀r². (9.17)




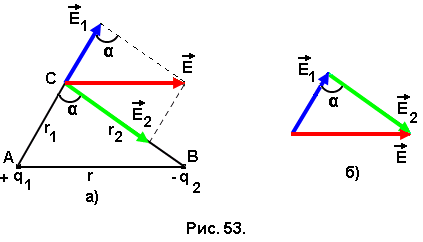
Напряжённость поля, созданного зарядом q₁ в точке С, равна

Е₁ = q₁ / 4πε₀r₁ ². (9.18)

Так как заряд q₁ положительный, то вектор Е₁ направлен от заряда q₁.

Напряжённость поля, созданного зарядом q₂ в точке С, равна

Е₂ = q₂ / 4πε₀r₂ ². (9.19)

Вектор Е₂ направлен к заряду q₂ , поскольку он является отрицательным.

Согласно принципу суперпозиции, напряжённость поля, созданного системой зарядов, определяется векторной суммой напряжённостей, созданных в этой точке каждым из зарядов этой системы. На рис. 53,а сложение векторов осуществлено по правилу параллелограмма, на рис. 53,б – по правилу треугольника.

Модуль вектора Е определим по теореме косинусов, согласно которой

Е² = Е₁² + Е₂² – 2Е₁Е₂ cos α. (9.20)

Для определения cos α запишем теорему косинусов для треугольника АВС:

r² = r₁² + r₂² – 2r₁r₂ cos α. (9.21)

Отсюда cos α = ( r₁² + r₂² - r²) / 2r₁r₂. (9.22)

Тогда Е = [Е₁² + Е₂² – Е₁Е₂ ( r₁² + r₂² - r²) / r₁r₂ ]^1/2 , (9.23)

где Е₁ и Е₂ рассчитаны по формулам (9.18) и (9.19).


Задача № 50. Частица массы 2m налетает на неподвижную частицу массы m. После столкновения частицы разлетаются симметрично под углом 45^о к направлению начальной скорости (рис.54,а). Во сколько раз возросла суммарная кинетическая энергия после столкновения?


По закону сохранения импульса геометрическая (векторная) сумма импульсов частиц после столкновения должна быть равна импульсу налетающей частицы массы 2m до столкновения (рис. 54,б). Так как углы при основании импульсного треугольника, каковым является вектор импульса р, равны между собой и равны 45^о, то импульсный треугольник является равнобедренным и прямоугольным. Отсюда следует, что импульсы частиц после столкновения равны по модулю: р₁ = р₂. (9.23)

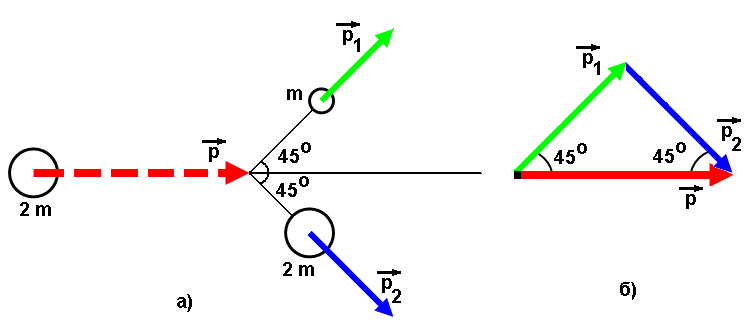Рис. 54.


Импульс налетающей частицы согласно (рис. 54,б) р = 2^1/2р₁ (9.24)

Кинетическая энергия налетающей частицы

Е_к = р²/4m = 2р₁²/ 4m = р₁²/ 2m . (9.25)

Суммарная кинетическая энергия частиц после столкновения равна:

Е_к1 + Е_к2 = (р₁²/ 2m) + (p₂²/ 4m) = 3p₁²/4m. (9.26)

Отношение суммарной кинетической энергии частиц после столкновения к кинетической энергии налетающей частицы равно:

(Е_к1 + Е_к2)/ Е_к = 3p₁² 2m / p₁² 4m = 3/2 = 1,5. (9.27)

Парадоксальность результата объясняется переходом собственной энергии частиц в кинетическую энергию их движения после столкновения.


Задача № 51. По двум длинным параллельным проводникам, расположенным на расстоянии r, текут токи I₁ и I₂ в направлениях, указанных на рис. 55,а, на котором изображены сечения проводников плоскостью, перпендикулярной им. Определить индукцию магнитного поля в точке, находящейся на расстоянии r₁ от первого проводника и на расстоянии r₂ от второго.







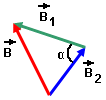
а) Рис. 55. б)


Линии магнитной индукции для прямого проводника с током являются концентрическими окружностями с центром на оси проводника, лежащими в плоскостях, перпендикулярных проводнику. Направление линий индукции определяется по правилу буравчика. Вектор магнитной индукции направлен по касательной к линии магнитной индукции и совпадает с ней по направлению. Если r₁ – радиус линии индукции магнитного поля проводника с током I₁, то вектор индукции В₁ перпендикулярен радиусу r₁. Аналогично вектор В₂ перпендикулярен радиусу r₂ линии индукции магнитного поля проводника с током I₂. Вектор магнитной индукции в указанной по условию точке согласно принципа суперпозиции складывается из векторов магнитной индукции В₁ и В₂. На рис. 55,а сложение произведено по правилу параллелограмма, а на рис. 55,б по правилу треугольника. Угол между векторами В₁ и В₂ (рис. 55,б) равен углу между r₁ и r₂ (рис. 55,а) как углы со взаимно перпендикулярными сторонами. Как и в задаче № 49 для определения модуля вектора В используем теорему косинусов, согласно которой

В = (В₁² + В₂² – 2В₁В₂ cos α)^1/2, (9.28)

а cos α по той же теореме, но только для треугольника r, r₁, r₂:

cos α = (r₁² + r₂² – r)/ 2r₁r₂. (9.29)

Тогда, В = [В₁² + В₂² – В₁В₂(r₁² + r₂² – r)/ r₁r₂]^1/2, (9.30)


§ 10. Метод решения обратной задачи.


Многие физические явления, изучаемые в школьном курсе физики, рассматриваются в идеальных условиях. При рассмотрении механических явлений часто пренебрегают сопротивлением среды, трением, рассеянием энергии, поэтому такие явления носят обратимый характер. Для таких случаев направление прямого процесса можно заменить обратным процессом.


Задача № 52. С какого расстояния S от центра полусферы радиуса R =1,35 м, с какой скоростью и под каким углом β нужно бросить маленькую шайбу (из положения 1), чтобы она, попав на полусферу, остановилась на её вершине (положение 2) (рис.56,а)? Трением шайбы о полусферу и сопротивлением воздуха пренебречь. Ускорение свободного падения считать равным 10 м/с².


Сформулируем обратную задачу: на каком расстоянии S от центра полусферы, с какой скоростью V и под каким углом β упадёт шайба, скатывающаяся с вершины полусферы радиуса R (рис. 56,б)? Трением шайбы о поверхность полусферы и сопротивлением воздуха пренебречь.


Определим, с какой скоростью V₀, под каким углом α к горизонту и с какой высоты от уровня основания полусферы (R cosα) отрывается шайба от поверхности полусферы. Точка отрыва лежит ниже вершины на расстоянии равном h, поэтому скорость шайбы в момент отрыва определится по формуле: V₀ = (2gh)^1/2. (9.31)

В момент отрыва шайбы от поверхности сферы сила реакции опоры становится равной нулю, сила трения равна нулю по условию, поэтому единственной силой, действующей на шайбу в этот момент, является сила тяжести. Точка отрыва шайбы является точкой перехода её траектории с дуги окружности радиуса R на параболическую кривую. Составляющая силы тяжести, действующая вдоль радиуса, является силой, сообщающей шайбе 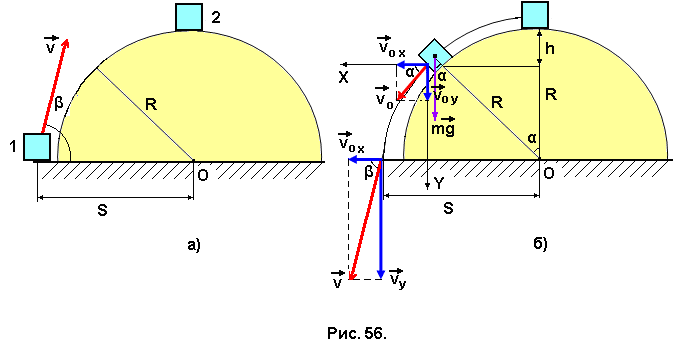центростремительное ускорение, поэтому скорость шайбы в момент отрыва можно определить по второму закону Ньютона:

mg cos α = m V₀²/R, откуда V₀ = (gR cosα)^1/2. (9.32)

Так как h = R(1 – cosα) (рис. 56,б), то: V₀ = [2gR (1 - cosα)]^1/2. (9.33)

Приравняв правые части равенств (9.32) и (9.33) определим косинус угла α, под которым направлен вектор V₀: cos α = 2/3. (9.34)

Подставив значение cos α в одно из уравнений (9.32) или (9.33), получаем значение скорости в момент отрыва шайбы:

V₀ = (2gR /3)^1/2 = (2 ^.10 ^.1,35 : 3)^1/2 = 3 м/с. (9.35)

Запишем уравнения движения шайбы после её отрыва в координатной форме, направив оси координат Х и У так, как показано на рис. 56,б:

Х = V_oxt = (V_o cosα)t; (9.36)

Y = V_oyt + gt²/2 = (V_o sin α)t +gt²/2 (9.37)

При t = t_п – времени полёта шайбы до точки падения, X = X_max, a

Y = R cos α = 1,35 ^. 2/3 = 0,9 м. Определим sin α = (1 – cos²α)^1/2 = (1 – 4/9)^1/2 = 5^1/2/3.

После подстановки t_п в уравнение (9.37) оно примет вид:

0,9 = 5^1/2t_п + 5t_п², (9.38)

откуда t_п = (5^1/2 + 23^1/2)/10 = 0,7 с.

Подставив значение t_п в (9.36) определим X_max = (V_o cosα)t_п = 3 ^. 2/3 ^. 0,7 = 1,4 м.

Точка падения шайбы лежит от центра полусферы на расстоянии

S = X_max + R sin α = 1,4 + 1,35 ^. 5^1/2/3 = 2,41 м.

Точка падения шайбы будет той точкой, откуда нужно бросить шайбу, чтобы она остановилась на вершине полусферы. Теперь определим скорость, с которой нужно бросить шайбу. Она будет равна скорости V, с которой шайба падает на горизонтальную поверхность:

V = (V_ox² + V_y²)^1/2 . (9.39)

V_ox = V_o cosα = 3 ^. 2/3 = 2 м; V_y = V_o sin α + gt_п = 3 ^. 5^1/2/3 + 10 ^. 0,7 = 9,24 м/с, подставив эти значения в (9.39), получим значение скорости

V = (2² + 9,24²)^1/2 = 9,45 м/с.

И, наконец, определим угол, под которым нужно направить вектор скорости V при бросании шайбы. Он будет равен углу β, под которым шайба падает на горизонтальную поверхность.

tg β = V_y / V_ox = 9,24/ 2 = 4,62; β = 77,8^o.

Таким образом, чтобы шайба, будучи брошенной, остановилась на вершине полусферы радиуса 1,35 м. её нужно бросить с расстояния 2,41 м от центра полусферы, со скоростью 9,45 м/с под углом 77,8^о к горизонтальной поверхности, на которой расположена полусфера.


§ 11. Обобщённые методы решения заданий базового, повышенного и высокого уровней сложности КИМов ЕГЭ.


Экзаменационная работа состоит из трёх частей. В первой части задания базового и повышенного уровней сложности с выбором ответа. Во второй – задания базового уровня со свободным ответом. В третьей – задания высокого уровня сложности.

Задания базового уровня проверяют усвоение базовых элементов знания и умения применять их в заданных ситуациях. Они представляют собой вопросы на воспроизведение теоретического материала или задачи на применение отдельного элемента знания в конкретной ситуации.

Задания повышенного уровня проверяют усвоение базовых элементов знания и умения применять отдельные элементы или несколько элементов в заданных или несколько изменённых ситуациях.

Задания высокого уровня проверяют комплексное использование знаний и умений из различных разделов курса физики.

Для задач базового уровня можно выделить общий метод решения, который содержит следующие предписания:

1. Установите явление, которому соответствует ситуация задачи.
   
2. Выделите элемент знания об этом явлении, указанный в вопросе задачи, с учётом условия задачи.
   
3. Дайте словесную формулировку элемента знания или запишите соответствующую формулу.
   
4. Примените формулировку или формулу к конкретной ситуации:
   

а) для элемента, который нельзя раскрыть в виде формулы, переведите формулировку в действие и выполните эти действия;

б) для формулы, по которой требуется провести расчёт, найдите в тексте задачи или рассчитайте значения величин в правой части формулы, подставьте эти значения в формулу, выразив их в одной системе единиц;

в) для формулы, по которой требуется провести сравнение, запишите формулу для одного случая, запишите формулу с коэффициентами, соответствующими заданному увеличению или уменьшению величин и рассчитайте искомый коэффициент.


Примеры заданий базового уровня.

Задача № 1. Установите, какой путь проходит крайняя точка винта взлетающего вертолёта в системе отсчёта, связанной с вертолётом, за время, равное периоду вращения. Радиус винта R.

Решение:

Путь - ? Путь – длина траектории. Траектория – окружность радиуса R. Период вращения – время одного оборота винта вокруг своей оси. За один оборот крайняя точка винта опишет длину окружности L = 2πR.


Задача № 2. Автомобиль первые 36 км пути прошёл со скоростью 10 м/с, затем 54 км пути со скоростью 15 м/с. Найдите среднюю скорость на всём пути.

Решение:

V_ср - ? V_ср = S/t; S = 36 + 54 = 90 км; t = t₁ + t₂ = (S₁/V₁) + (S₂/V₂) = (36000/10) + (54000/15) = 7200 c; V_ср = 90000/7200 =12,5 м/с.


Задача № 3. Два тела свободно падают без начальной скорости, причём первое с высоты в 4 раза большей, чем второе. Сравните время падения первого и второго тел.

Решение:

t₁/t₂ = ? h = gt²/ 2; h = gt₁²/2; 4h = gt₂²/2; ¼ = t₁²/ t₂²; t₁/ t₂ = 1/2; t₂ = 2 t₁.


Задания повышенного уровня сложности представляют собой задачи на применение системы знаний об одном из явлений, изучавшихся в какой-либо теме школьного курса физики, и являются типовыми задачами. В работе [ 9 ] предлагается представлять решение таких задач в свёрнутом виде.


Примеры решения задач в свёрнутом виде.


Задача №1. С высоты 5 м бросают вертикально вверх тело массой 200 г с начальной скоростью 2 м/с. Какую скорость будет иметь тело при падении на землю? Сопротивлением воздуха пренебречь. Ответ запишите с точностью до 0,1.

Решение:

Модель ситуации Уравнения Расчёт




mgh + mv₀²/2 = mv²|2 v = (2gh + v₀²)^1/2

v = (2^.10^.5 + 4)^1/2 ≈ 10,2 м/c


Задача № 2. Мальчик массой 50 кг, стоя на очень гладком льду, бросает груз массой 8 кг под углом 60^о к горизонту со скоростью 5 м/с. Какую скорость приобретёт мальчик?

Решение:

Модель ситуации Уравнения Расчёт




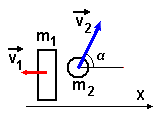
m₂v₂ cos α - m₁v₁ = 0 v₁ = (m₂/m₁)v₂ cos α


v₁ = 8^.5 cos 60^o/50 = 0,4 м/с


Задания высокого уровня представляют собой задачи на применение систем знаний о нескольких явлениях из какого-либо раздела школьного курса физики. Для этих задач требуется оформить развёрнутый ответ [ 9 ].


Задача № 3. Груз массой 0,1 кг, подвешенный на нити длиной 1 м, отклонен на угол α от вертикального положения и отпущен. Сила натяжения нити в момент прохождения грузом положения равновесия равна 2 Н. Чему равен угол α?

Решение:

Дано:	Модель ситуации:	Система уравнений:
L = 1 м m = 0,1 кг F упр = 2 H g = 10 м/с2		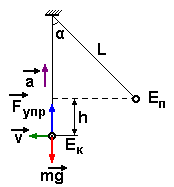2 gh = v2 Fупр - mg = ma h = L(1 – cos α) a = v2/L
		Расчётная формула:
		cos α = (3 mg – Fупр) / 2mg
		Расчёт:
α -- ?		cos α = (3.0,1.10 – 2) / 2. .0,1.10 = 0,5
		Ответ: α = 60о