Программа элективного курса по информатике для предпрофильной подготовки «Некоторые методы решения логических задач»
| Вид материала | Программа |
- Рабочая программа элективного курса по информатике «Приёмы решения нестандартных задач, 219.89kb.
- Программа элективного курса по географии для 9 класса в рамках предпрофильной подготовки, 270.03kb.
- Рабочая программа элективного курса предпрофильной подготовки в 9-ом классе по математике, 75.07kb.
- Рабочая программа Элективного курса «Методы решения физических задач» в 9 классе, 221.38kb.
- Программа элективного курса предпрофильной подготовки «Кожа зеркало здоровья», 83.86kb.
- Программа элективного курса по русскому языку и литературе 9 класс, 83.37kb.
- Программа элективного курса предпрофильной подготовки по теме: «Юность экономической, 251.68kb.
- Программа элективного курса предпрофильной подготовки и профильного обучения «Введение, 91.03kb.
- Программа предметно ориентированного элективного курса для предпрофильной подготовки, 179.82kb.
- Программа элективного курса предпрофильной подготовки и профильного обучения «ссср, 149.31kb.
ПРОГРАММА
элективного курса по информатике
для предпрофильной подготовки
«Некоторые методы решения логических задач».
В.М. Таутинова, учитель информатики и математики
высшей квалификационной категории
МОУ-СОШ с. Кировское
Марксовского района Саратовской области
Пояснительная записка.
Для некоторых людей решение логических задач – увлекательное и несложное занятие. Легко распутывая клубок противоречивых высказываний, они приходят к правильному ответу необычайно быстро.
Но, к сожалению, ход логических рассуждений нельзя свести к одной двум стандартным схемам. Логические задачи разнообразны, как разнообразны и описываемые в них ситуации.
Алгоритмический подход к решению логических задач, рассматриваемых в данном элективном курсе, позволит более широкому кругу обучающихся научиться решать логические задачи определенного типа.
В данном курсе подробно рассматриваются методы решения логических задач на приведение элементов двух или трех множеств во взаимнооднозначное соответствие, логические задачи, решаемые с помощью кругов Эйлера, а также задачи на переливания жидкости.
Данный элективный курс рекомендуется для учеников 9 классов и призван реализовать следующие цели:
образовательно-содержательная цель:
– обучить учащихся решению предлагаемых видов логических задач;
развивающая цель:
– через решение логических задач развивать алгоритмическое мышление, а также умение анализировать, синтезировать, обобщать;
воспитательная цель:
– посредством организации занятий воспитывать настойчивость в достижении цели, интерес к математической логике.
Задачами курса являются:
- формирование у обучающихся устойчивого интереса к математической логике;
- расширение знаний о методах и способах решения логических задач;
- формирование умения моделировать реальные ситуации.
Программа элективного курса рассчитана на 9 часов, включает теоретический материал, практические занятия по решению задач, итоговое занятие в виде зачета.
Занятия элективного курса рекомендуется проводить по классно-урочной системе.
Планируемые результаты обучения
В результате изучения элективного курса учащиеся должны:
-понимать сущность понятия "логическая задача";
-знать алгоритмы решения алгоритмических логических задач и уметь применять их на практике.
Учебно-тематический план курса (9ч.)
| № темы | Тема | Количество часов |
| 1 | Метод таблиц | 1 |
| 2 | Решение логических задач с помощью трехмерной таблицы | 2 |
| 3 | Решение логических задач с помощью кругов Эйлера | 2 |
| 4 | Задачи на переливания жидкости. Метод блок-схем | 1 |
| 5 | Задачи на переливания жидкости. Метод бильярда | 2 |
| 6 | Зачет | 1 |
Основное содержание курса.
Тема 1. Метод таблиц.
Многие логические задачи связаны с рассмотрением нескольких конечных множеств с одинаковым количеством элементов, между которыми имеются некоторые зависимости. Требуется установить взаимнооднозначное соответствие между элементами данных множеств.
Решение такого типа задач оформляется в виде таблицы. Элементы одного множества располагаются по строкам, другого – по столбцам. Если по условию задачи между элементами множеств есть соответствие, то в клетке на пересечении данных строки и столбца ставится «плюс», в случае отсутствия зависимости – «минус». Если в какой-то строке или столбце имеется «плюс», то в оставшихся незаполненных клетках этой строки или столбца проставляются «минусы». Если во всех клетках строки или столбца, кроме одной, имеются «минусы», то в незаполненной клетке ставится «плюс». Это объясняется тем, что между элементами данных множеств соответствие должно быть взаимнооднозначным.
Рассмотрим этот метод на примере конкретной задачи.
В одном доме живут Воронов, Павлов, Журавлев, Синицын. Один из них – математик, другой – художник, третий – писатель, а четвертый – баянист. Известно, что:
- ни Воронов, ни Журавлев не умеют играть на баяне;
- Журавлев не знаком с Вороновым;
- писатель и художник в воскресенье уезжают на дачу к Павлову;
- писатель собирается написать очерк о Синицыне и Воронове.
Требуется определить, кто есть кто.
Решение.
Начнем решение задачи с построения логического квадрата. Элементы первого множества (фамилии) запишем в строках, а элементы второго множества (профессии) расположим в столбцах.
| | математик | художник | писатель | баянист |
| Воронов | | | | |
| Павлов | | | | |
| Журавлев | | | | |
| Синицын | | | | |
А теперь проведем анализ условия задачи, сделаем на его основе выводы и зафиксируем их в таблице. Из условия 1 следует, что ни Воронов, ни Журавлев баянистами быть не могут. Поставим в соответствующих клетках (на пересечении фамилий и профессий) «минусы».
| | математик | художник | писатель | баянист |
| Воронов | | | | – |
| Павлов | | | | |
| Журавлев | | | | – |
| Синицын | | | | |
Из условия 3 ясно, что Павлов не может быть ни писателем, ни художником. Занесем в таблицу и это.
| | математик | художник | писатель | баянист |
| Воронов | | | | – |
| Павлов | | – | – | |
| Журавлев | | | | – |
| Синицын | | | | |
Условие 4 приводит к выводу, что Синицын и Воронов не могут быть писателями. Отметим это в таблице.
| | математик | художник | писатель | баянист |
| Воронов | | | – | – |
| Павлов | | – | – | |
| Журавлев | | | | – |
| Синицын | | | – | |
Мы видим, что в столбце «писатель», «минусами» заполнены все клетки, кроме одной, говорящей о том, что Журавлев может быть только писателем, и никем иным. Отметим этот вывод и поставим в соответствующей клетке «плюс». А поскольку, согласно условию задачи, речь идет только об одном писателе, то и в строке «Журавлев», в оставшихся незаполненных клетках, проставляем «минусы».
| | математик | художник | писатель | баянист |
| Воронов | | | – | – |
| Павлов | | – | – | |
| Журавлев | – | – | + | – |
| Синицын | | | – | |
Так как Журавлев – писатель, а также из условий 2 и 3 следует, что Воронов не может быть художником. Отметим это в таблице.
| | математик | художник | писатель | баянист |
| Воронов | | – | – | – |
| Павлов | | – | – | |
| Журавлев | – | – | + | – |
| Синицын | | | – | |
Из таблицы видно, что все остальные незаполненные клетки можно заполнить, используя основное правило табличного способа решения логических задач.
| | математик | художник | писатель | баянист |
| Воронов | + | – | – | – |
| Павлов | – | – | – | + |
| Журавлев | – | – | + | – |
| Синицын | – | + | – | – |
Таким образом, мы видим, что Воронов – математик, Павлов – баянист, Журавлев – писатель, а Синицын – художник.
Тема 2. Решение логических задач с помощью трехмерной таблицы.
Если в логической задаче нужно привести в соответствие элементы не двух, а трех множеств, то удобнее воспользоваться методом решения логических задач с помощью трехмерной таблицы.
Суть этого метода состоит в следующем:
- Строится пространственная система координат XYZ, на осях проставляются названия множеств и элементы этих множеств.
- Читается условие задачи. Если пара элементов в двух множествах находится в соответствии, то точка, лежащая на пересечении соответствующих прямых, становится центром темного кружка, в противном случае – белого кружка.
- Применяется правило экстраполяции:
«Темная» экстраполяция. Если на горизонтали (вертикали) все фигуры, кроме одной, светлы, то свободная занимается темной фигурой.
«Светлая» экстраполяция. Если на горизонтали (вертикали) имеется «темная» фигура, то все остальные фигуры на ней – светлые.
Множественная экстраполяция. Если две (n) параллели в плоскости одинаково светло раскрашены, везде, за исключением двух (n) неокрашенных вершин, то на двух (n) параллелях другого направления, проходящих через эти вершины, вне данных прямых вставляются светлые фигуры.
- Применяется правило множественного проектирования:
«Темная» фигура в своей плоскости проектируется на координатные оси. Прямые, проведенные через проекции в двух других плоскостях, раскрашиваются одинаково.
- Повторяются шаги 3) - 4) пока это возможно.
- Если в сложившейся ситуации возможности экстраполяции и проектирования исчерпаны, а задача не решена, то делается допущение о цвете фигуры в какой-либо свободной вершине сетки. В случае противоречия допущение отклоняется, и цвет фигуры в данной точке меняется на противоположный.
Алгоритм этого метода раскроем в ходе решения следующей задачи:
Маша, Лида, Женя и Катя играют на разных инструментах – баяне, рояле, гитаре, скрипке, но каждая на одном. Они же владеют иностранными языками – английским, французским, немецким, испанским, но каждая одним.
Девушка, играющая на гитаре, говорит по-испански. Ни Лида, ни Маша не играют на скрипке и баяне, не знают английского языка. Девушка, которая говорит по-немецки, не играет на баяне. Женя знает французский язык, но не играет на скрипке.
Кто играет на каком инструменте и каким иностранным языком владеет?
Решение.
Построим пространственную систему координат XYZ, на осях проставим названия множеств и элементы этих множеств.
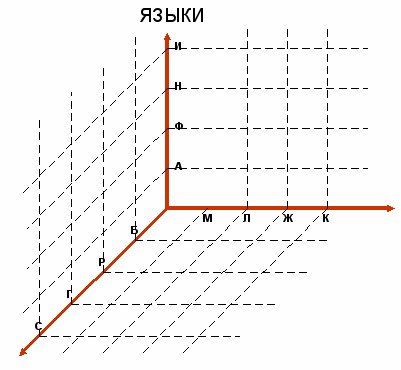
ИМЕНА
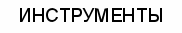
ИМЕНА
М – Маша
Л – Лида
Ж – Женя
К – Катя
ЯЗЫКИ
А – Английский
Ф – Французский
Н – Немецкий
И – Испанский
ИНСТРУМЕНТЫ
Б – Баян
Р – Рояль
Г – Гитара
С – Скрипка
В
нимательно прочитав условие задачи, отметим черными и белыми кружками соответствия и несоответствия пар элементов двух множеств. После этого наша таблица будет выглядеть следующим образом:ИНСТРУМЕНТЫ
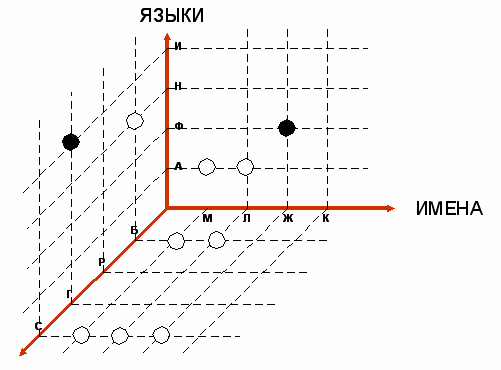
А теперь будем применять правила «темной» и «светлой» экстраполяций пока это возможно. В результате применения этих правил, таблица приобретет следующий вид:
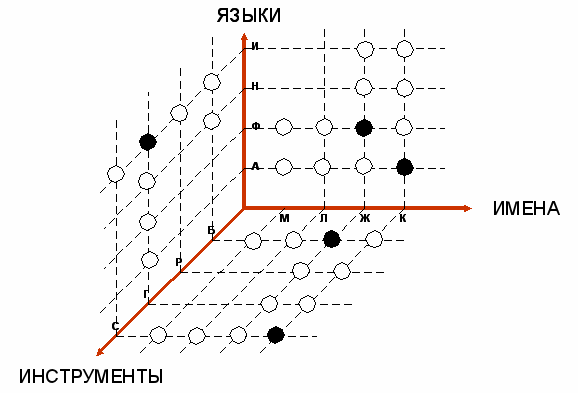
В
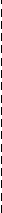плоскости XZ к «темным» фигурам, находящимся на пересечениях элементов Ж и Б, К и С применим правило множественного проектирования.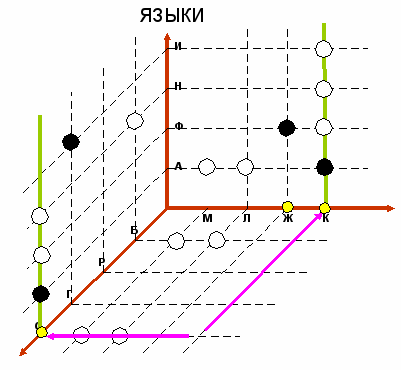 
ЯЗЫКИ
ЯЗЫКИ
И
И
Н
Н
Ф
Ф
А
А
ИМЕНА
ИМЕНА
Л
Ж
К
М
Б
Л
Ж
К
М
Б
Р
Р
Г
С
С
ИНСТРУМЕНТЫ
ИНСТРУМЕНТЫ
И
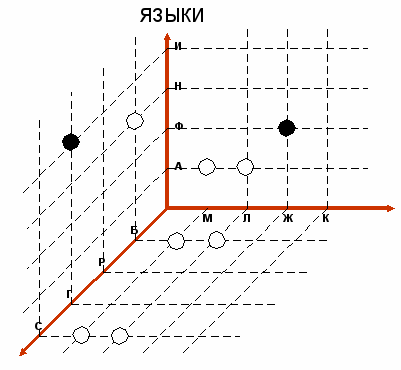вновь применим «темную» и «светлую» экстраполяции.ЯЗЫКИ
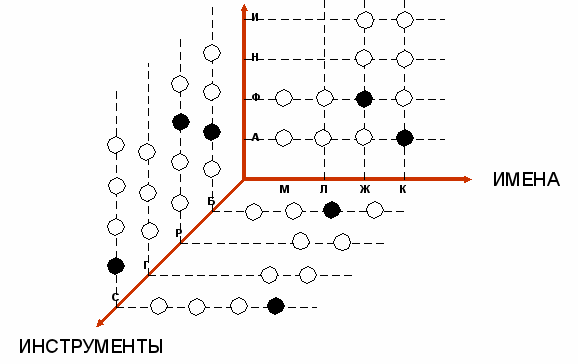
В сложившейся ситуации возможности экстраполяций и проектирования исчерпаны, а задача не решена. В таких случаях делается допущение о цвете фигуры в какой-либо свободной вершине сетки.
Пусть точка, лежащая на пересечении элементов М и Н, станет центром «темного» кружка. Сделав это предположение, повторим правила экстраполяций и множественного проектирования.
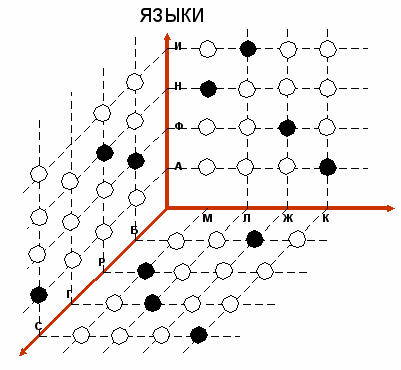
ИМЕНА
ИНСТРУМЕНТЫ
При допущении о цвете фигуры в свободной вершине сетки мы не получили противоречия, поэтому можно считать, что задача решена верно. Итак, мы узнали, что Маша играет на рояле и владеет немецким языком, Лида играет на гитаре и знает испанский язык, Женя играет на баяне и владеет французским языком, Катя играет на скрипке и знает английский язык.
А теперь, чтобы проверить, не имеет ли данная задача двух верных решений, вернемся назад и предположим противное: пусть точка, лежащая на пересечении элементов М и Н, станет центром не «темного», а светлого кружка. После применения правил экстраполяций и множественного проектирования, таблица заполнится следующим образом.
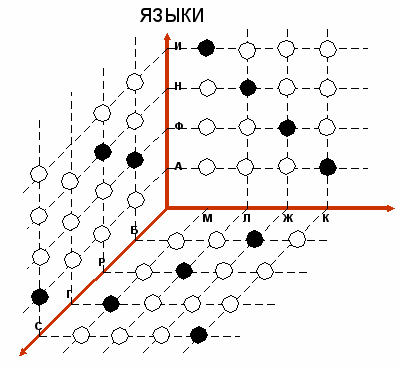
ИМЕНА
ИНСТРУМЕНТЫ
В заполненной таблице мы также не видим противоречия, это означает, что полученное решение, тоже удовлетворяет заданным условиям, т.е. задача имеет два решения. Согласно второму решению, Маша играет на гитаре и владеет испанским языком, Лида играет на рояле и знает немецкий язык, Женя играет на баяне и владеет французским языком, Катя играет на скрипке и знает английский язык.
Этот метод решения логических задач имеет преимущество перед обычным табличным способом. В пространственной системе координат все данные условия задачи можно отметить сразу. Затем, используя правила экстраполяций и множественного проектирования, не анализируя находящуюся в таблице информацию, можно прийти к правильному решению (в двумерной таблице, такое условие, как, например, девушка, играющая на гитаре, говорит по-испански, сразу в таблице не отметишь, к этому условию приходится возвращаться после анализа и сопоставления других фактов).
Табличные способы решения логических задач наглядны, но не обладают универсальностью, т.е. предназначены для решения только одного типа задач, когда нужно привести в соответствие элементы двух или трех множеств.
Тема 3. Решение логических задач с помощью кругов Эйлера.
Упростить решение многих логических задач помогают так называемые круги Эйлера, с помощью которых можно изобразить множество элементов, обладающих определенным свойством.
Рассмотрим задачу. В туристической группе из 100 человек 75 человек знают немецкий язык, 65 человек – английский язык, а 10 человек – не знают ни немецкого, ни английского языка. Сколько туристов знают два языка?
Решение. Изобразим условие задачи в виде кругов Эйлера. В большом круге, изображающем 100 туристов, поместим 2 меньших круга, изображающих знатоков английского и немецкого я
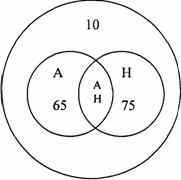зыков.Легко видеть, что 90 туристов (100-10) знают хотя бы один язык; 15 туристов (90-75) знают только английский язык, 75-15=50 – туристов знают оба языка.
Ответ: 50 туристов.
Задача. В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение. Д - драмкружок; Х - хор; С - спорт. В круге Д - 27 ребят, в круге Х - 32 человека, в круге С - 22 ученика.
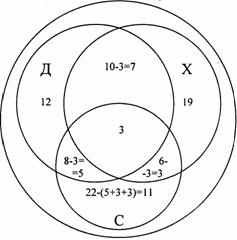
Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8-3=5 спортсменов, не поющих в хоре и 6-3=3, не посещающих драмкружок. Легко видеть, что 5+3+3=11 спортсменов посещают хор или драмкружок, 22-(5+3+3)=11 заняты только спортом; 70-(11+12+19+7+3+3+5)=10 - не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.
Ответ: 10 человек.
Тема 4. Метод блок-схем.
Рассмотрим еще один тип логических задач. Это задачи на переливания, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости. Такие задачи можно решить методом перебора всевозможных вариантов, но в этом случае трудно удержать в памяти все звенья логических рассуждений.
Задачи на переливания удобнее решать методом блок-схем, в котором используются условные команды. Рассмотрим этот метод подробнее. Для начала введем сокращенные обозначения для операций, которые могут быть использованы: НБ – наполнить больший сосуд; ОМ – опустошить меньший сосуд; Б→М – перелить из большего сосуда в меньший, пока больший сосуд не опустеет или меньший не наполнится. Кроме этих трех операций введем сокращенные обозначения и для условий, которые будут использоваться в блок-схеме: Б=0? – посмотреть, пуст ли больший сосуд; МН? — посмотреть, наполнен ли малый сосуд.
Изобразим последовательность команд в виде блок-схемы.
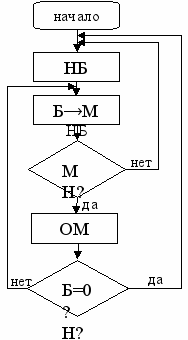
Последовательность переливаний, изображенная на блок-схеме следующая: сначала наполняется больший сосуд, затем вода из большего сосуда переливается в меньший. Всякий раз, когда меньший сосуд наполняется, он опустошается, и всякий раз, когда больший сосуд опустошается, он заново наполняется.
Решим методом блок-схем следующую задачу: имеются два сосуда – трехлитровый и пятилитровый, нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.
Решение.
Будем фиксировать, как меняется количество воды в сосудах, если действовать по приведенной блок-схеме. Результаты оформим в виде таблицы.
-
т
5 л
аблица переливаний
0
3 л
5
2
2
0
5
4
4
1
1
0
5
3
3
0
0
0
3 л + 5 л
0
3
0
2
2
3
0
3
0
1
1
3
0
3
0
0
5
5
2
2
7
7
4
4
1
1
6
6
3
3
0
Дальше эта последовательность будет полностью повторяться. Из таблицы видно, что количество воды в обоих сосудах вместе образует следующую последовательность: 0, 5, 2, 7, 4, 1, 6, 3, 0 и т.д. Таким образом, действуя по приведенной схеме, можно отмерить любое количество литров от 1 до 7. Чтобы отмерить еще и 8 литров, надо наполнить оба сосуда.
Если сначала наполнить меньший сосуд, то блок-схема, изображающая последовательность переливаний, будет выглядеть следующим образом (обозначения аналогичные):
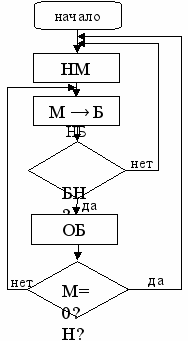
Из блок-схемы видно, что сначала наполняется меньший сосуд, затем вода из меньшего сосуда переливается в больший. Всякий раз, когда больший сосуд наполняется, он опустошается, и всякий раз, когда меньший сосуд опустошается, он наполняется заново.
| таблица переливаний | |||||||||||||||
| 0 | 3 | 0 | 3 | 1 | 1 | 0 | 3 | 0 | 3 | 2 | 2 | 0 | 3 | 0 | 0 |
| 0 | 0 | 3 | 3 | 5 | 0 | 1 | 1 | 4 | 4 | 5 | 0 | 2 | 2 | 5 | 0 |
| 0 | 3 | 3 | 6 | 6 | 1 | 1 | 4 | 4 | 7 | 7 | 2 | 2 | 5 | 5 | 0 |
3 л
5 л
3 л + 5 л
По таблице переливаний мы видим, что количество воды в обоих сосудах вместе образуют такую же последовательность, как и в предыдущем случае, только записанную в обратном порядке: 0, 3, 6, 1, 4, 7, 2, 5, 0.
Для получения четырех литров воды количество шагов в обеих блок-схемах одинаковое. Но, если, например, нужно получить два литра воды, то удобнее воспользоваться первой блок-схемой, а если нужно получить один литр воды, то лучше действовать по второй блок-схеме. Но определить, какой путь более короткий, по блок-схемам сложно, так как данный метод не обладает достаточной наглядностью.
Тема 5. Метод бильярда.
Задачи на переливание жидкостей можно очень легко решать, вычерчивая бильярдную траекторию шара, отражающегося от бортов стола, имеющего форму параллелограмма.
Рассмотрим задачу. Пусть имеются два сосуда – трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 4 литра воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.
Решение.
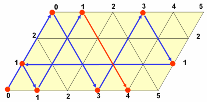
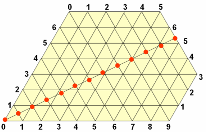
В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников.
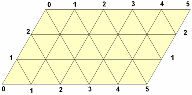
Бильярдный шар может перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль линии сетки, выходящей из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов.
Пусть шар находится в левом нижнем углу и после удара начнет перемещаться вверх вдоль левой боковой стороны параллелограмма до тех пор, пока не достигнет верхней стороны. Это означает, что мы полностью
наполнили водой малый сосуд. Отразившись упруго, шар покатится вправо вниз и ударится о нижний борт в точке, координаты которой 3 по горизонтали и 0 по вертикали. Это означает, что в большом сосуде 3 литра воды, а в малом сосуде воды нет, то есть мы перелили воду из малого сосуда в большой сосуд.
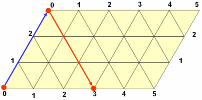
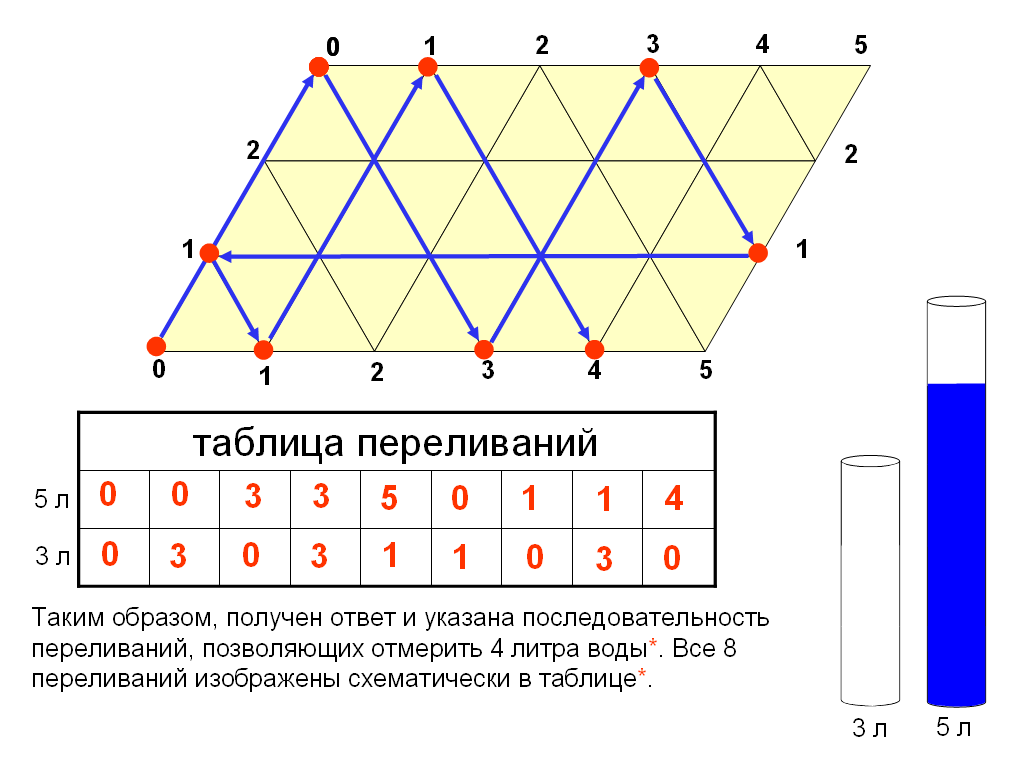
Прослеживая дальнейший путь шара, и записывая все этапы его движения в виде отдельной таблицы, в конце концов, мы попадаем в точку, которая соответствует состоянию, когда малый сосуд пуст, а в большом сосуде 4 литра воды. Таким образом, мы получаем ответ и последовательность переливаний, позволяющих отмерить 4 литра воды. Все 8 переливаний изображены схематически на рисунке и в таблице.
| таблица переливаний | ||||||||
| 0 | 0 | 3 | 3 | 5 | 0 | 1 | 1 | 4 |
| 0 | 3 | 0 | 3 | 1 | 1 | 0 | 3 | 0 |
3 л
5 л
Е
сли на диаграмме шар из начальной точки покатится вправо по нижней стороне параллелограмма и затем, отразившись от правой боковой стороны, в точку 2 на верхней стороне параллелограмма и т.д., то можно получить более короткое решение задачи.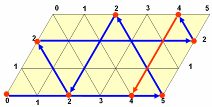 
| таблица переливаний | |||||||
| 0 | 5 | 2 | 2 | 0 | 5 | 4 | 4 |
| 0 | 0 | 3 | 0 | 2 | 2 | 3 | 0 |
5 л
3 л
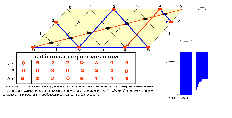
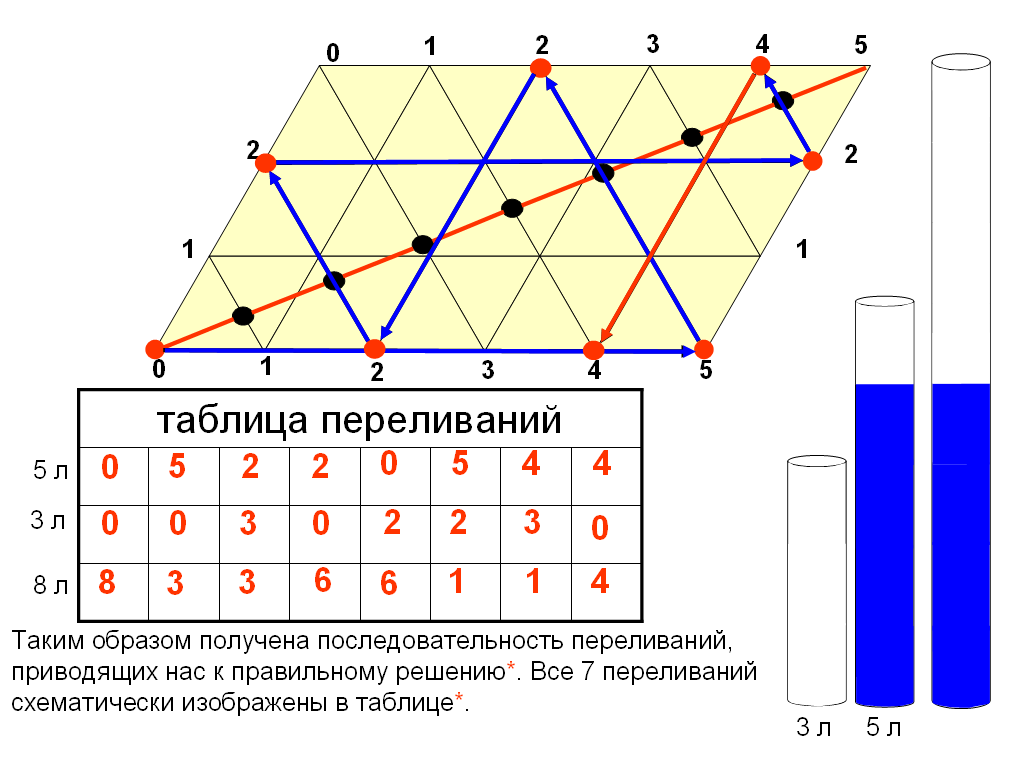
А теперь рассмотрим задачу на переливания, по условию которой используются три сосуда. Пусть восьмилитровый сосуд до краев наполнен водой. С помощью двух пустых сосудов емкостью 3 и 5 литров надо поровну разделить воду в два больших сосуда.
Решение.
Д
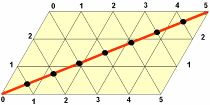иаграмма для этой задачи точно такая же – параллелограмм со сторонами 5 и 3 единицы. Чтобы фиксировать количество воды в третьем, восьмилитровом сосуде, дополнительно проведем главную диагональ параллелограмма.Она делится наклонными прямыми на 8 частей. Отметив точку деления, начиная с верхней правой вершины параллелограмма, получаем возможность фиксировать количество воды в третьем, восьмилитровом, сосуде. Первые две координаты любой точки параллелограмма, куда может попасть бильярдный шар, определяются, как и выше, а третья координата равна величине отрезка, отсекаемого на главной диагонали соответствующей наклонной. Как и раньше, шар начинает движение от точки с координатами (0;0). Нарисовав траекторию шара, получим решение с числом переливаний, равным 7.
Если объемы двух меньших сосудов не имеют общего делителя (т.е. взаимно просты), а объем третьего сосуда больше или равен сумме объемов двух меньших, то с помощью этих трех сосудов можно отмерить любое целое число литров, начиная с 1 литра и кончая объемом среднего сосуда. Имея, например, сосуды вместимостью 7, 8 и 15 литров, можно отмерить любое количество воды от 1 до 8 литров. Такая процедура невозможна, если объемы двух меньших сосудов имеют общий делитель, так как в этом случае шар будет двигаться по одной и той же траектории.
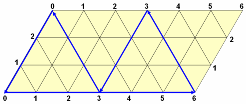
К
огда объем большего сосуда меньше суммы объемов двух других, возникают новые ограничения. Если, например, объемы сосудов равны 7, 9 и 12 литров, то у параллелограмма надо отсечь верхний правый угол. Это происходит потому, что на диагонали должно быть отложено не более 12 единиц.Отметим, что бильярдный шар может попасть в любую точку от 1 до 9, за исключением точки 6. Легко видеть, что точки с цифрой 6 образуют на диаграмме правильный треугольник, и мы не можем никак попасть на этот треугольник из любой другой точки, лежащей вне этого треугольника.
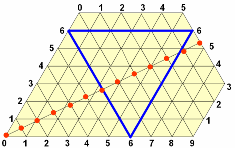
Таким образом, несмотря на то, что 7 и 9 взаимно просты, отмерить 6 литров воды оказывается невозможным из-за того, что самый большой сосуд имеет слишком маленький объем. Отметим также, что обобщение метода математического бильярда на случай четырех сосудов сводится к движению шара в пространственной области (параллелепипеде). Но возникающие при этом трудности изображения траекторий делают метод неудобным.
ЗАДАЧИ.
Задачи на приведение множеств во взаимнооднозначное соответствие.
1. Аня, Женя, Нина спросили, какие оценки им поставили за контрольную работу по математике. Учитель ответил: "Плохих оценок нет. У вас троих оценки разные. У Ани не "3". У Нины не "3" и не "5"". Кто, какую оценку получил?
2. Коля, Боря, Вова, Юра заняли первые четыре места в соревнованиях. На вопрос, какие места они заняли, трое ответили: Коля - ни 1-е, ни 4-е; Боря - 2-е; Вова - не 4-е. Какие места заняли мальчики?
3. В симфонический оркестр приняли на работу трёх музыкантов: Бориса, Сергея и Витю, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
Сергей самый высокий;
играющий на скрипке меньше ростом играющего на флейте;
играющие на скрипке и флейте и Борис любят пиццу;
когда между альтистом и трубачом возникает ссора, Сергей мирит их;
Борис не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
4. Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
5. Три дочери писательницы Дорис Кей — Джуди, Айрис и Линда, тоже очень талантливы. Они приобрели известность в разных видах искусств — пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго.
Известно, что:
Джуди живет не в Париже, а Линда — не в Риме;
парижанка не снимается в кино;
та, кто живет в Риме, певица;
Линда равнодушна к балету.
Где живет Айрис, и какова ее профессия?
6. Три девочки — Роза, Маргарита и Анюта представили на конкурс цветоводов корзины выращенных ими роз, маргариток и анютиных глазок. Девочка, вырастившая маргаритки, обратила внимание Розы на то, что ни у одной из девочек имя не совпадает с названием любимых цветов.
Какие цветы вырастила каждая из девочек?
7. Ирена, Тимур, Камилла, Эльдар и Залим стали победителями олимпиад школьников по физике, математике, информатике, литературе и географии.
Известно, что:
победитель олимпиады по информатике учит Ирену и Тимура работе на компьютере;
Камилла и Эльдар тоже заинтересовались информатикой;
Тимур всегда побаивался физики;
Камилла, Тимур и победитель олимпиады по литературе занимаются плаванием;
Тимур и Камилла поздравили победителя олимпиады по математике;
Ирена cожалеет о том, что у нее остается мало времени на литературу.
Победителем какой олимпиады стал каждый из этих ребят?
Задачи, решаемые с помощью кругов Эйлера.
1. Часть жителей одного городка умеют говорить только по-русски, часть только - по белоруски, а часть – умеет говорить на обоих языках. По-русски говорят 75%, а по-белорусски – 85% жителей. Сколько процентов жителей говорят на обоих языках?
2. В классе 38 человек. Из них 16 играют в баскетбол, 17 – в хоккей, 18 – в волейбол. Увлекаются двумя видами спорта – баскетболом и хоккеем – четверо, баскетболом и волейболом – трое, волейболом и хоккеем – пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни волейболом. Сколько ребят одновременно увлекаются тремя видами спорта? Сколько ребят увлекаются только одним из этих видов спорта?
3. В классе учатся 40 человек. Из них по русскому языку имеют "3" 19 человек, по математике – 17 человек и по физике – 22 человека. Только по одному предмету имеют "тройки": по русскому языку – 4 человека, по математике – 4 человека и по физике – 11 человек. Семь человек имеют "тройки" и по математике и по физике, из них пятеро имеют тройки по русскому языку. Сколько человек учатся без троек? Сколько человек имеют тройки по двум из трёх предметов?
4. Каждый из 40 человек, путешествующий автобусом "Граунд" знает не менее одного иностранного языка: английский, немецкий, французский. 36 человек знают хотя бы один из двух языков: английский, немецкий. 19 человек – хотя бы один из языков: немецкий, французский; 8 человек – только немецкий. Одновременно два языка – английский и немецкий – изучают на 5 человек больше, чем французский и немецкий языки. Сколько человек изучают каждый из языков и сколько изучают каждую пару языков?
5. Контрольная работа по математике состояла из задачи, уравнения и неравенства. Контрольную работу писали 40 человек. Правильно решили только задачу 2 ученика, только неравенство – 4 человека, только уравнение – 3 человека. Не решили только задачу 7 человек, только уравнение – 5 человек, только пример – 6 человек. Остальные выполнили всю работу правильно. Сколько таких учащихся?
6. Пол комнаты площадью 12 м2 покрыт тремя коврами: площадь одного ковра 5 м2, другого – 4 м2 и третьего – Зм2. Каждые два ковра перекрываются на площади 1,5 м2, причём 0,5 м2 из этих полутора квадратных метров приходится на участок пола, где перекрываются все три ковра. Какова площадь пола, не покрытая коврами? Какова площадь пола, покрытого только одним первым ковром?
Литература
- Лихтарников Л.М., Сукачева Т.Г. Математическая логика /Курс лекций / Оформление обложки А. Олексенко, С. Шапиро. - СПб.: Издательство "Лань", 1998. - 288с.
- Лыскова В.Ю., Ракитина Е.А. Логика в информатике. - М.: Лаборатория базовых знаний, 2001. - 160 с.: ил. Серия "Информатика".
- Т.С. Кармакова, О.В.Сташко «Логические задачи», М. 2001 г.
- В.И.Курбатов « Как развить свое логическое мышление.»- М. «Зевс», 1997 г.