Geum.ru

Лобанов Владимир Иванович, вед научн сотрудник фгуп «цнии «Комета», к т. н., e mail : lobanov V i @ mail ru

Вид материалаДокументы

Содержание


1. Алгебра логики
1.2 Основные законы алгебры Буля.
Особое место в алгебре логики занимает функция импликации
Подобный материал:
1   2   3   4   5   6   7

1. Алгебра логики

1.1 Основные положения алгебры логики



Логика – наука о законах мышления. Она позволяет делать правильные выводы из любых посылок, предохраняет от ошибок в рассуждениях, обеспечивает безошибочное доказательство всевозможных законов, правил и теорем в различных областях знаний: в математике, физике, химии, в грамматике русского языка и т.п. Для решения этих задач используется алгебра логики.

В алгебре логики (булевой алгебре) переменные могут принимать два значения: 1 (истинно) или 0 (ложно). Для двух аргументов существуют 16 логических функций (операций, логических действий). Полная система этих функций(z0 – z15) для двух аргументов(x,y) показана в таблице.




Над переменными в основном производятся три логических действия: сложение, умножение, отрицание (инверсия), что соответствует функциям ИЛИ, И, НЕ. Все функции в булевой алгебре могут быть описаны с помощью таблицы истинности. В нижеследующих таблицах описаны функции И(z1), ИЛИ(z7),НЕ(z12).



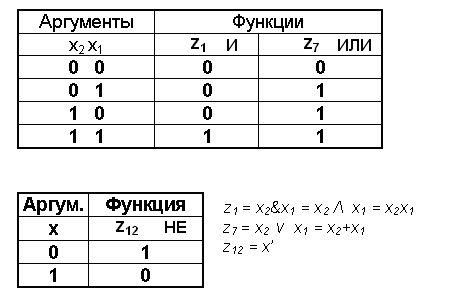
Вместо функции И часто используется термин «конъюнкция», вместо функции ИЛИ - термин «дизъюнкция». Вместо функции НЕ употребляется термин «инверсия» или «отрицание». Для двоичной логики понятия «инверсия» и «отрицание» эквивалентны.

При написании логических формул для функции И используются следующие символы: &, Λ, точка или ее отсутствие; для функции ИЛИ - V, +. Функция НЕ обозначается штрихом над аргументом. Мы для обозначения отрицания будем использовать апостроф. Таким образом, можно записать:

z1 = x2 & x1 = x2 Λ x1 = x2x1 z7 = x2 V x1 = x2 + x1

z12 = x’

Какой смысл имеют логические функции И, ИЛИ, НЕ. Поясним это на примерах. Пусть школьник принял решение: « Я пойду в кино, если выучу уроки и покатаюсь на лыжах». Обозначим через f1 – «я пойду в кино», x1 – «я выучу уроки», x2 – «я покатаюсь на лыжах». Тогда решение школьника будет записано в виде логической формулы так:

f1 = x2x1.

Родители заявили ученику: «Ты посмотришь телефильм, если перед этим покатаешься на лыжах или поиграешь в хоккей». Пусть f2 – «посмотришь телефильм», x1 – «покатаешься на лыжах», x2 – «поиграешь в хоккей». Тогда заявление родителей можно представить в виде логической формулы так:

f2 = x2+x1.

Тренер сказал футболисту-юниору: «Ты останешься в команде, если у тебя не будет двоек». Пусть f3 – «ты останешься в команде», x – «будут двойки», тогда приказ тренера выразится следующей формулой: f3 = x’.

1.2 Основные законы алгебры Буля.



Прежде, чем приступить к изложению основных законов алгебры логики, зафиксируем некоторые очевидные её положения.

1 + a = 1; 0 + a = a; a & 1 = a; a & 0 = 0; a + a’ = 1.

Эти соотношения легко проверяются по таблице истинности для логической функции ИЛИ подстановкой 0 или 1 вместо аргумента a.





В булевой алгебре все операции осуществляются с логическими переменными и подчиняются законам алгебры логики. Опишем и докажем некоторые из них.

а) Переместительный закон

а + в = в + а; ав = ва

б) Сочетательный закон

( а + в ) + с = а + ( в + с) ; ( ав )с = а(вс)

в) Распределительный закон

а( в + с ) = ав + ас ; а + вс = (а + в)( а+с )

г) Закон поглощения

а + ав = а( 1 + в ) = а ; а( а + в ) = а + ав = а

д) Закон склеивания

ав + ав’ = а(в + в’) = a & 1 = a; ( а + в )(а + в’) = а

е) Идемпотентный закон

a + a = a; a & a = a

Вышеприведённые законы легко проверяются подстановкой 0 и 1 вместо аргументов a, b, c.

ё) Правила де Моргана

Эти правила справедливы для любого числа аргументов.

а + в + с + .... + z = ( а’в’с’...z’ )’

авс... = ( а’ + в’ + с’ + ... + z’ )’

Правила можно описать таким алгоритмом.

Для перехода от логической суммы к логическому произведению необходимо проделать следующие операции:

1) проинвертировать все слагаемые в отдельности;

2) заменить знаки сложения знаками умножения;

3) проинвертировать получившееся выражение.

Аналогично выполняется переход от логического произведения к логической сумме. В инженерной практике используются лишь правила де Моргана и закон склеивания.

Кроме основных функций И(f1), ИЛИ(f2), НЕ(f3), в алгебре логики часто используются функции равнозначности (эквивалентности) и неравнозначности (сумма по модулю 2). Для обозначения этих функций применяют следующие символы: равнозначность - ~ и =, сумма по модулю 2 -  и ≠. Содержание этих функций отражено в таблице.



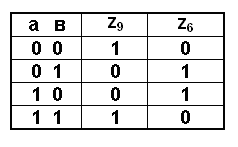
Смысл этой таблицы прост: если a = b, то функция равнозначности z9 = 1. Если же a  b, то z9 = 0, а функция неравнозначности z6 = 1. Для того, чтобы по таблице истинности построить булеву функцию, достаточно выписать все наборы входных переменных и представить их в виде логической суммы. Если какая-либо переменная входит в набор нулём, то она в символьном виде отображается своей инверсией.

Из таблицы получаем:

z9 = а ~ в = 00 + 11 = а’в’ + ав – равнозначность;

z6 = a  в = 01 + 10 = а’в + ав’ – сумма по модулю 2, или неравнозначность.

Из таблицы видно, что

z9 = z6’ или z9’ = z6 .

Таким образом,

а’в’ + ав = ( ав’ + а’в )’, или

а~в = ( а  в )’, а  в = (а~в)’.


Особое место в алгебре логики занимает функция импликации: a→b = a’+b. Переводится приведённая формула импликации на русский язык так: если истинно a, то b тоже истинно. Например, пусть a – я выучу все энциклопедии, а b – обыграю всех телезнатоков. Тогда запись a→b будет означать следующее суждение: если я выучу все энциклопедии, то обыграю всех телезнатоков.

Все вышеприведённые правила и законы даны не для запоминания-зубрёжки, а в качестве справочного материала. Нужно никогда не забывать, что главным инструментом является Ваша светлая голова, Ваше мышление.