Лобанов Владимир Иванович, вед научн сотрудник фгуп «цнии «Комета», к т. н., e mail : lobanov V i @ mail ru

Вид материала

Содержание

1.3. Синтез логических функций
Алгоритм «НИИРТА» графической минимизации булевых функций от 4-х и менее переменных.
Формы задания булевых функций.

Подобный материал:

1 2 3 4 5 6 7

1.3. Синтез логических функций

Под синтезом логических функций будем понимать процесс её получения по словесному описанию, по таблице истинности или любому другому способу задания этой функции. Синтез логических функций можно проиллюстрировать решением простой задачи.

Задача 1.1.

Приёмная комиссия в составе трех членов комиссии и одного председателя решает судьбу абитуриента большинством голосов. В случае равного распределения голосов большинство определяется голосом председателя. Найти краткое определение ситуации, в которой абитуриент будет принят в учебное заведение. Найти решение в виде логической функции, т.е. построить автомат для тайного голосования.

Решение.

Пусть f - функция большинства голосов. f = 1, если большинство членов комиссии проголосовало за приём абитуриента, и f = 0 в противном случае.

Обозначим через x₄ голос председателя комиссии. x₄ = 1, если председатель комиссии проголосовал за приём абитуриента. x₃, x₂, x₁- голоса членов приёмной комиссии.

С учётом вышеуказанных допущений условие задачи можно однозначно представить в виде таблицы истинности.

Заполнение таблицы осуществляем с учётом того, что функция f является полностью определённой, т.е. она определена на всех возможных наборах переменных x₁- x₄. Для n входных переменных существует N = 2ⁿ наборов переменных. В нашем примере N = 2⁴ = 16 наборов.

Записывать эти наборы можно в любом порядке, но лучше в порядке возрастания двоичного кода.

Примечание. Здесь и далее под набором будем понимать конъюнкцию, т.е. логическое произведение, всех входных переменных.

Все наборы, на которых функция принимает значение 1 , будем называть единичными, или рабочими. Наборы, на которых функция принимает значение 0, будем называть нулевыми, или запрещенными (по Мавренкову Л.Т.).

Для того, чтобы по таблице истинности найти функцию f, достаточно выписать все единичные наборы и соединить их знаком дизъюнкции.

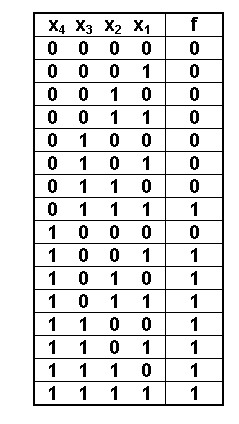
Таким образом,

f = 0111+1001+1010+1011+1100+1101+1110+1111

или в символьном виде

f = x₄’x₃x₂x₁+x₄x₃’x₂’x₁+x₄x₃’x₂x₁’+x₄x₃’x₂x₁+x₄x₃x₂’x₁’+x₄x₃x₂’x₁+

+x₄x₃x₂x₁’+x₄x₃x₂x₁

Полученная форма функции называется совершенной дизъюнктивной нормальной формой (СДНФ), здесь каждое логическое слагаемое представляет собой конъюнкцию всех аргументов. В случае, когда не каждое слагаемое представляет собой конъюнкцию всех аргументов, то такая форма представления логической функции называется просто ДНФ. Очевидно, применяя основные законы булевой алгебры, мы могли бы аналитически уменьшить сложность полученного выражения. Но это наихудший способ минимизации булевых функций.

1.4.Минимизация полностью определённых булевых функций.

Карты Карно позволяют решить задачу минимизации логической функции элегантно и просто. Карно был толковым инженером (кстати, за 30 лет я так и не нашёл его биографии: узнал только, что это американец 20-го столетия), но поленился или не сумел описать алгоритм работы со своими картами. Поэтому до сих пор неблагодарное человечество не научилось работать с ними. Алгоритм работы с картами Карно (этот алгоритм не известен ни одному логику в мире) был разработан автором более 30 лет назад [2 - 10]. Здесь алгоритм приводится в сокращённом варианте.

Алгоритм «НИИРТА» графической минимизации булевых функций от 4-х и менее переменных.

1. Заполнить карту Карно (КК) нулями и единицами в соответствии с таблицей истинности или заданным алгебраическим выражением.

2. Покрыть все элементарные квадраты Карно, в которых записаны единицы, минимальным количеством прямоугольников Карно (ПК), каждый из которых имеет максимальную площадь.

3. Каждому прямоугольнику Карно соответствует одна импликанта (логическое слагаемое), причём если в границах прямоугольника Карно какая-либо переменная принимает значения как 0 , так и 1 , то эта переменная склеивается, т.е. удаляется из импликанты.

Под прямоугольником Карно (этот термин пришлось ввести в 1977г.) для не более чем от 4-х аргументов, можно понимать любую, в том числе и разорванную, симметричную фигуру покрытия, количество клеток (элементарных прямоугольников Карно) в которой составляет целую степень двойки: 1, 2, 4, 8. Все клетки ПК являются соседними, т.е. закодированы соседними кодами. Два кода называются соседними, если они отличаются друг от друга только в одном разряде. Например, коды 1010 и 1011 являются соседними.

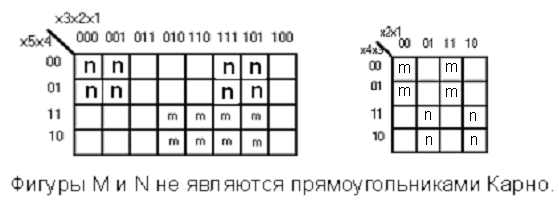
На нижеприведённом рисунке даны примеры КК и прямоугольников Карно для различного числа аргументов.

На КК для 4-х переменных представлены два прямоугольника Карно, один из которых (Р) является разорванной фигурой покрытия. На КК для 6 переменных изображены прямоугольники Карно A – G, K, M, N, большинство из которых также являются разорванными фигурами покрытия. Общее для всех свойство - симметричность по Лобанову [2 - 4], необходимое и достаточное условие для определения ПК.

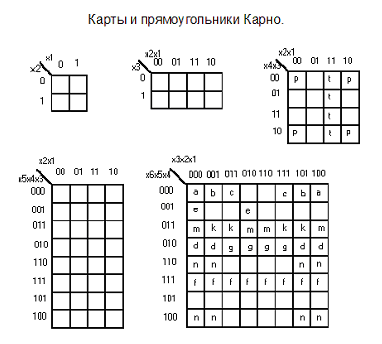
В современной логике появились попытки представить ПК просто фигурой покрытия с 2ⁿ клетками КК. Пример фигур покрытия, содержащих 2³ клеток КК и не являющихся прямоугольниками Карно, представлен на следующем рисунке. Фигуры М и N не обладают симметричностью по Лобанову.

Решение задачи 1.1 с помощью карты Карно представлено на рисунке.

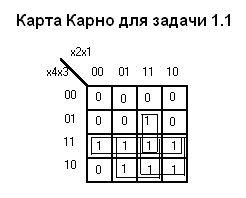
Из карты Карно получено соотношение:

f = x₄x₁ + x₄x₂ + x₄x₃ + x₃x₂x₁

Это выражение представляет собой пример минимальной дизъюнктивной нормальной формы (МДНФ). В некоторых случаях приведение результата минимизации к скобочной форме (вынесение общего множителя за скобки) позволяет уменьшить количество интегральных схем (ИС), необходимых для реализации булевой функции. Скобочная форма для f имеет вид:

f = x₄(x₁ + x₂ + x₃) + x₃x₂x₁

Смысл скобочной формулы прост: за абитуриента должны проголосовать либо все 3 члена комиссии, либо хотя бы один из них, но совместно с председателем.

Формы задания булевых функций.

Об одной форме задания булевых функций мы уже говорили - это таблица истинности. Иногда применяется более компактная запись, использующая двоичные, восьмеричные, десятичные или шестнадцатеричные эквиваленты наборов. Это так называемые обобщённые коды. Например, набор x₄x₃x₂’x₁’ может быть представлен обобщённым двоичным кодом 1100 , десятичным эквивалентом которого является число 12. Удобнее всего 8-чные и 16-чные коды. Автором создана Паскаль-программа синтеза псевдослучайных кодов для задания произвольных булевых функций при проведении семинаров или контрольных работ. Эту программу можно разработать самостоятельно или найти её на сайте ссылка скрыта [7].

Поскольку мы будем работать с функциями не более чем от 4-х переменных, то нам пригодится таблица перевода 10-чисел от 0 до 15 в двоичные коды.

Десятичное число	Двоичное число	Десятичное число	Двоичное число
0	0000	8	1000
1	0001	9	1001
2	0010	10	1010
3	0011	11	1011
4	0100	12	1100
5	0101	13	1101
6	0110	14	1110
7	0111	15	1111