Лобанов Владимир Иванович, вед научн сотрудник фгуп «цнии «Комета», к т. н., e mail : lobanov V i @ mail ru
| Вид материала | Документы |
Содержание1.5. Минимизация недоопределённых булевых функций |
- -, 1113.42kb.
- Конспект лекций по предмету технология программирования базовая кафедра №248 при фгуп, 929.64kb.
- Арушанова Алла Генриховна к п. н., ведущий научный сотрудник, лауреат премии правительства, 164.19kb.
- Решение уравнений Максвелла Дирака дают солитонные уравнения, которые предполагают, 160.73kb.
- Мнение ветеринарного врача со стажем об иммуномодуляторах и иммуностимуляторах для, 354.58kb.
- Сухин Игорь Георгиевич, старший научный сотрудник Института теории и истории педагогики, 214.89kb.
- с) 1999 А. Аливердиев (e-mail: aliverdi@mail, 1826.11kb.
- Нп «сибирская ассоциация консультантов», 69.44kb.
- Берестовая Жанна Александровна, методист гцро, тел. 74-57-34; e-mail: metodist-70@mail, 43.21kb.
- Россия. Москва, ул. Сущевский вал, д. 47, стр. 2, оф. 1, Пц «Маэстро» (конкурс), 127.12kb.
1.5. Минимизация недоопределённых булевых функций
Функция от n переменных называется недоопределённой, если она задана не на всех 2n наборах. Задача минимизации такой функции заключается в оптимальном доопределении значений функции на незаданных наборах, которое позволило бы покрыть рабочие наборы минимальным количеством прямоугольников Карно, каждый из которых имел бы максимальную площадь.
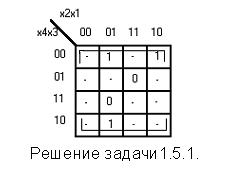
Задача 1.5.1.
Найти минимальную форму функции y от 4-х аргументов, заданную десятичными рабочими (РН) и запрещёнными (ЗН) наборами:
РН(4): 1, 2, 9;
ЗН(4): 7, 13.
Решение.
Функция задана только на 5 наборах (число в скобках указывает количество переменных). Добавим к трём рабочим наборам ещё пять, а именно : 0000, 0011, 1000, 1011, 1010. Все оставшиеся наборы доопределим как запрещённые. В результате такого доопределения получим прямоугольник Карно, состоящий из 8 элементарных квадратов Карно. Этому прямоугольнику соответствует функция:
y = х3’
Задание 2.
2-1. Построить по заданной таблице истинности 2/(2-10) преобразователь для делителя частоты на 24, работающего в коде 16-8-4-2-1. Этот преобразователь использовался на заре цифровой схемотехники в радиолюбительских электронных часах.
| x4 x3 x2 x1 x0 | y5 y4 | y3 y2 y1 y0 | x4 x3 x2 x1 x0 | y5 y4 | y3 y2 y1 y0 |
| 0 0 0 0 0 | 0 0 | 0 0 0 0 | 0 1 1 0 0 | 0 1 | 0 0 1 0 |
| 0 0 0 0 1 | 0 0 | 0 0 0 1 | 0 1 1 0 1 | 0 1 | 0 0 1 1 |
| 0 0 0 1 0 | 0 0 | 0 0 1 0 | 0 1 1 1 0 | 0 1 | 0 1 0 0 |
| 0 0 0 1 1 | 0 0 | 0 0 1 1 | 0 1 1 1 1 | 0 1 | 0 1 0 1 |
| 0 0 1 0 0 | 0 0 | 0 1 0 0 | 1 0 0 0 0 | 0 1 | 0 1 1 0 |
| 0 0 1 0 1 | 0 0 | 0 1 0 1 | 1 0 0 0 1 | 0 1 | 0 1 1 1 |
| 0 0 1 1 0 | 0 0 | 0 1 1 0 | 1 0 0 1 0 | 0 1 | 1 0 0 0 |
| 0 0 1 1 1 | 0 0 | 0 1 1 1 | 1 0 0 1 1 | 0 1 | 1 0 0 1 |
| 0 1 0 0 0 | 0 0 | 1 0 0 0 | 1 0 1 0 0 | 1 0 | 0 0 0 0 |
| 0 1 0 0 1 | 0 0 | 1 0 0 1 | 1 0 1 0 1 | 1 0 | 0 0 0 1 |
| 0 1 0 1 0 | 0 1 | 0 0 0 0 | 1 0 1 1 0 | 1 0 | 0 0 1 0 |
| 0 1 0 1 1 | 0 1 | 0 0 0 1 | 1 0 1 1 1 | 1 0 | 0 0 1 1 |
2-2. Построить 4-входовой сумматор для суммирования одноразрядных двоичных чисел по заданной таблице истинности.
| x4x3x2x1 | y2y1y0 | x4x3x2x1 | y2y1y0 |
| 0 0 0 0 | 0 0 0 | 1 0 0 0 | 0 0 1 |
| 0 0 0 1 | 0 0 1 | 1 0 0 1 | 0 1 0 |
| 0 0 1 0 | 0 0 1 | 1 0 1 0 | 0 1 0 |
| 0 0 1 1 | 0 1 0 | 1 0 1 1 | 0 1 1 |
| 0 1 0 0 | 0 0 1 | 1 1 0 0 | 0 1 0 |
| 0 1 0 1 | 0 1 0 | 1 1 0 1 | 0 1 1 |
| 0 1 1 0 | 0 1 0 | 1 1 1 0 | 0 1 1 |
| 0 1 1 1 | 0 1 1 | 1 1 1 1 | 1 0 0 |
1.6. Практикум по синтезу и минимизации логических функций.
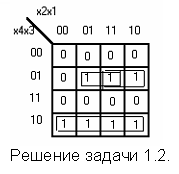
Задача 1.2.
Полностью определённая булева функция от 4-х переменных задана десятичными рабочими наборами: РН(4) = 5, 6, 7, 8, 9, 10, 11.Число в скобках указывает количество переменных. Найти минимальную форму этой функции.
Решение.
Так как функция является полностью определённой, то запрещёнными наборами ЗН(4) являются наборы 0 - 4, 12 - 15. Исходя из этой информации, составляем таблицу истинности и осуществляем минимизацию по карте Карно.
Таблица 4.
-
РН(4)
x4 x3 x2 x1
f
5
0 1 0 1
1
6
0 1 1 0
1
7
0 1 1 1
1
8
1 0 0 0
1
9
1 0 0 1
1
10
1 0 1 0
1
11
1 0 1 1
1
-
ЗН(4)
x4 x3 x2 x1
f
0
0 0 0 0
0
1
0 0 0 1
0
2
0 0 1 0
0
3
0 0 1 1
0
4
0 1 0 0
0
12
1 1 0 0
0
13
1 1 0 1
0
14
1 1 1 0
0
15
1 1 1 1
0
По карте Карно получаем результат: f = x4x3’ + x4’x3(x1 + x2)
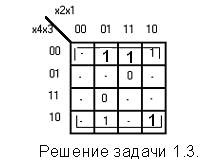
Задача 1.3.
Найти минимальную форму функции y, представленной на рисунке.
Решение.
Функция задана только на 7 наборах. Добавим к пяти рабочим наборам ещё три, а именно : 0000, 1000, 1011. Все оставшиеся наборы доопределим как запрещённые. В результате такого доопределения получим прямоугольник Карно, состоящий из 8 элементарных квадратов Карно. Этому прямоугольнику соответствует функция: y = x3’
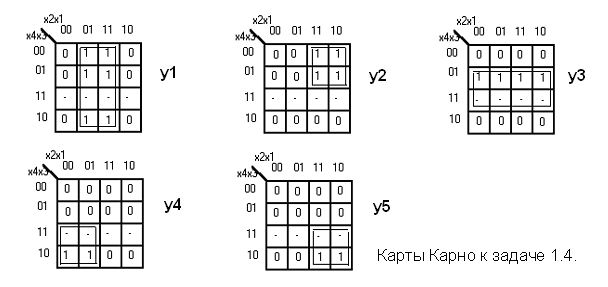
Задача 1.4.
Построить преобразователь двоичного кода в двоично-десятичный в соответствии с таблицей.
| x4x3x2x1 | y5y4y3y2y1 | x4x3x2x1 | y5y4y3y2y1 |
| 0 0 0 0 | 0 0 0 0 0 | 0 1 1 0 | 0 0 1 1 0 |
| 0 0 0 1 | 0 0 0 0 1 | 0 1 1 1 | 0 0 1 1 1 |
| 0 0 1 0 | 0 0 0 1 0 | 1 0 0 0 | 0 1 0 0 0 |
| 0 0 1 1 | 0 0 0 1 1 | 1 0 0 1 | 0 1 0 0 1 |
| 0 1 0 0 | 0 0 1 0 0 | 1 0 1 0 | 1 0 0 0 0 |
| 0 1 0 1 | 0 0 1 0 1 | 1 0 1 1 | 1 0 0 0 1 |
Решение.
Для каждой функции yi заполняем карту Карно, производим доопределение и осуществляем минимизацию. Весь процесс отражён на рисунке.
В результате минимизации получаем систему функций:
y1 = x1 y2 = x4’x2 y3 = x3 y4 = x4x2’ y5 = x4x2
Задача 1.5.
Построить один разряд многоразрядного сумматора, заданного таблицей истинности. Здесь ai и вi - значения i-ых разрядов слагаемых а и в , Pi и Si - значения переноса и суммы на выходе i-го разряда, Pi-1 - значение переноса на выходе предыдущего разряда.
| ai вi Pi-1 | Pi | Si |
| 0 0 0 | 0 | 0 |
| 0 0 1 | 0 | 1 |
| 0 1 0 | 0 | 1 |
| 0 1 1 | 1 | 0 |
| 1 0 0 | 0 | 1 |
| 1 0 1 | 1 | 0 |
| 1 1 0 | 1 | 0 |
| 1 1 1 | 1 | 1 |
Решение.
Имеем систему полностью определённых булевых функций. Производим раздельную минимизацию каждой функции (см. рисунок).
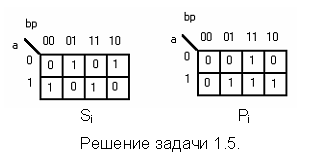
Из карт Карно после минимизации получаем следующие результаты.
Si = ai’вi’Pi-1 + ai’вiPi-1’ + aiвi’Pi-1’ + aiвiPi-1
Pi = вiPi-1 + aiPi-1 + aiвi
