Принятие решений в условиях неопределенности

Вид материала

Документы

Содержание Принятие решений в условиях неопределенности. Элементы теории статистических решений 1.2.Игры с природой в условиях неопределенности. Оптимистическая позиция Позиция нейтралитета Особые случаи

Подобный материал:

• 5 семестр. Контрольные вопросы для подготовки к экзамену: Игры с природой. Принятие, 40.09kb.
• Интеллектуальные технологии в управлении предприятием, 117.18kb.
• Конспект лекций Математические методы и модели в экономике, 46.08kb.
• 1. Анализ предпринимательских рисков инструментами финансового анализа и финансового, 129.75kb.
• Принятие решений в процессе управления строительным предприятием в условиях неопределенности, 386.26kb.
• Особенности преподавания элементов теории риска на экономических специальностях вузов, 48.21kb.
• Методические указания Объектом исследования теории игр (ТИ) является принятие решений, 145.42kb.
• Тема: Процессы принятия решений в организации, 22.07kb.
• Лекция 03. 04. 07 Принятие решений как функция менеджмента, 65.61kb.
• Многокритериальные методы обоснования управленческих решений в условиях нестохастической, 189.79kb.

Принятие решений в условиях неопределенности. Элементы теории статистических решений

Предметом рассмотрения данного раздела служат статистические модели принятия решений, трактуемые как статистические игры или игры с Природой при использовании дополнительной статистической информации о её стратегиях. Характерная черта статистической игры – возможность получения информации в результате некоторого статистического эксперимента для оценки распределения вероятностей стратегий природы. Исследование механизма случайного выбора стратегии природой позволяет принять оптимальное решение, которое будет наилучшей стратегией в игре с неантагонистическим противником человека – природой.

В рассмотренных разделах теории игр предполагалось, что оба противника (или больше двух) активно противодействуют друг другу, что оба они достаточно умны, чтобы искать и найти свою оптимальную стратегию, и осторожны, чтобы не отступать от нее. Такое положение дает возможность предсказывать поведение игроков. Неопределенность была лишь в выборе противником конкретной чистой стратегии в каждой отдельной партии.

Но возможен случай, когда неопределенность в игре вызвана не сознательным противодействием противника, а незнанием условий, в которых будет приниматься решение, случайных обстоятельств. Такие игры называются "играми с природой".

Игра человека с природой тоже отражает конфликтную ситуацию, возникающую при столкновении интересов в выборе решения. Но "стихийным силам природы" нельзя приписать разумные действия, направленные против человека и тем более какой-либо "злой умысел". Таким образом, корректнее говорить о конфликтной ситуации, вызванной столкновением интересов человека и неопределенностью действий природы.

Действия природы могут, как наносить ущерб, так и приносить прибыль. Поведение природы можно оценить статистическими методами, определить присущие ей закономерности. В зависимости от степени знания этих закономерностей, определяющих поведение природы, различаются игры с природой в условиях определенности и игры с природой в условиях неопределенности.

Во-первых, поведение природы известно полностью (заданы вероятностями). Во-вторых - действия природы не известны, или изучены частично.

К явлениям природы, влияющим на результат решения, относят не только погодные и сезонные явления (дождь, засуху, урожай, неурожай), но и проявление любых, не зависящих от нас обстоятельств: например, задержки на транспорте.

Поиском решений в таких ситуациях и занимается теория статистических решений.

Человек, играя с природой, стремиться максимизировать свой выигрыш, поэтому, если он осторожный игрок (а теория игр рассматривает именно таких игроков), он должен при выборе своей стратегии руководствоваться тем, что неизвестные или известные ему закономерные действия природы приведут к наименее благоприятным последствиям. Именно поэтому такие игры можно рассматривать как игры двух лиц с нулевой суммой, которые были уже нами рассмотрены.

Формализация задачи происходит следующим образом: у активного игрока (человека) возможные действия по-прежнему называются стратегиями, а возможные действия пассивного игрока (природы) – состояниями или условиями природы.

В качестве первого игрока всегда выступает человек, поэтому в матрице записывается его выигрыш. Так как нас интересует оптимальная стратегия человека и его гарантированный выигрыш, то в игру достаточно определить максиминную стратегию первого игрока и нижнюю цену игры. Определение верхней цены игры имеет смысл, если данная игра повторяется многократно и оптимальная стратегия может быть смешанной.

1.2.Игры с природой в условиях неопределенности.

Если распределение вероятностей будущих состояний природы неизвестно, вся информация о природе сводится к перечню ее возможных состояний. Человек в играх с природой старается действовать осмотрительно, второй игрок (природа, например, покупательский спрос) действует случайно. Таким образом, в сложных структурах каждому допустимому варианту решений Xi вследствие различных внешних условий могут соответствовать различные внешние условия (состояния) Вj и результаты аij решений. Следующий пример иллюстрирует это положение.

Пусть из некоторого материала требуется изготовить изделие, долговечность которого при допустимых затратах невозможно определить. Нагрузки считаются известными. Требуется решить, какие размеры должно иметь изделие из данного материала [Э. Мушик, П. Мюллер. Методы принятия технических решений. М.: Мир, 1990. – 2008 с.].

Варианты решений таковы:

X₁ – выбор размеров из соображений максимальной долговечности, т.е. изготовление изделия с минимальными затратами в предположении, что материал будет сохранять свои характеристики в течение длительного времени;

Xn – выбор размеров в предположении минимальной долговечности;

Xi – промежуточные решения.

Условия (состояния), требующие рассмотрения, таковы:

В₁ – условия, обеспечивающие максимальную долговечность;

Вm – условия, обеспечивающие минимальную долговечность;

Вj – промежуточные условия.

Под результатом решения аij здесь можно понимать оценку, соответствующую варианту Xi и условиям Вj и характеризующую экономический эффект (прибыль), полезность или надёжность изделия. Семейство решений описывается некоторой матрицей nm, которую называют матрицей решений (условия игры задаются матрицей nm). По аналогии с теорией игр, эту матрицу будем называть также платёжной матрицей.

Таблица. 7 Матрица решений (nm

Условия Варианты	B1	B2	B3		Bj		Bm
X1	a11	a12	a13		a1j		a1m
X2	a21	a22	a23		a2j		a2m
X3	a31	a32	a33		a3j		a3m
Xi	ai1	ai2	ai3		aij		aim
Xn	am1	am2	am3		anj		anm

Конструктор старается выбрать решение с наилучшим результатом, но, так как ему неизвестно, с какими условиями он столкнётся, он вынужден принимать во внимание все оценки аij, соответствующие варианту Xi.

Оценочная функция

Чтобы прийти к однозначному и по возможности наивыгоднейшему варианту решений даже в том случае, когда каким-то вариантам решений Xi могут соответствовать различные условия Вj, можно ввести подходящие оценочные (целевые) функции. При этом матрица решений сводится к одному столбцу. Каждому варианту Xi приписывается, таким образом, некоторый результат аir, характеризующий, в целом, все последствия этого решения. Такой результат мы в дальнейшем будем обозначать тем же символом аir.

Рассмотрим некоторые оценочные функции, которые в данном примере мог бы выбрать конструктор.

Оптимистическая позиция:

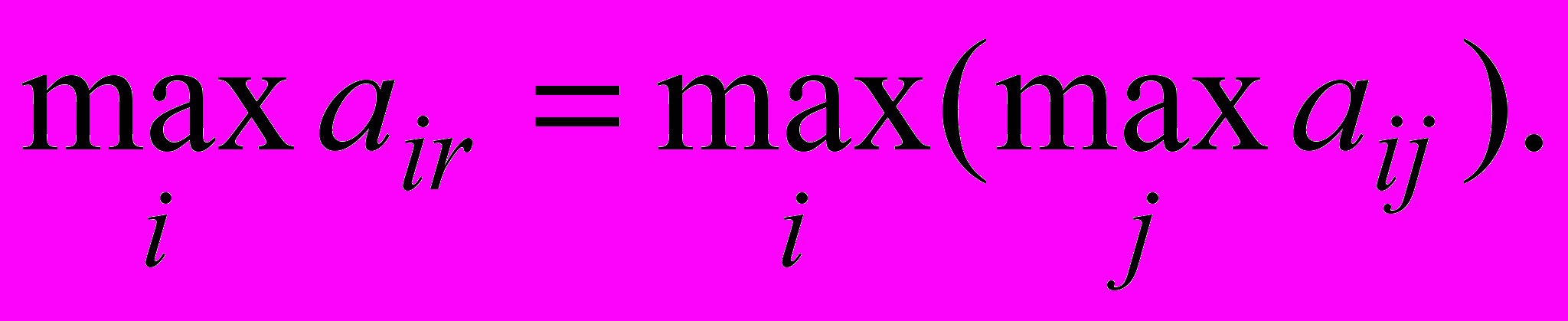(1)

Из матрицы результатов решений выбирается вариант (строка), содержащий в качестве возможного следствия наибольший из всех возможных результатов. Наш конструктор становится на точку зрения азартного игрока. Он делает ставку на то, что выпадет наивыгоднейший случай, и, исходя из этого, выбирает размеры изделия.

Позиция нейтралитета:

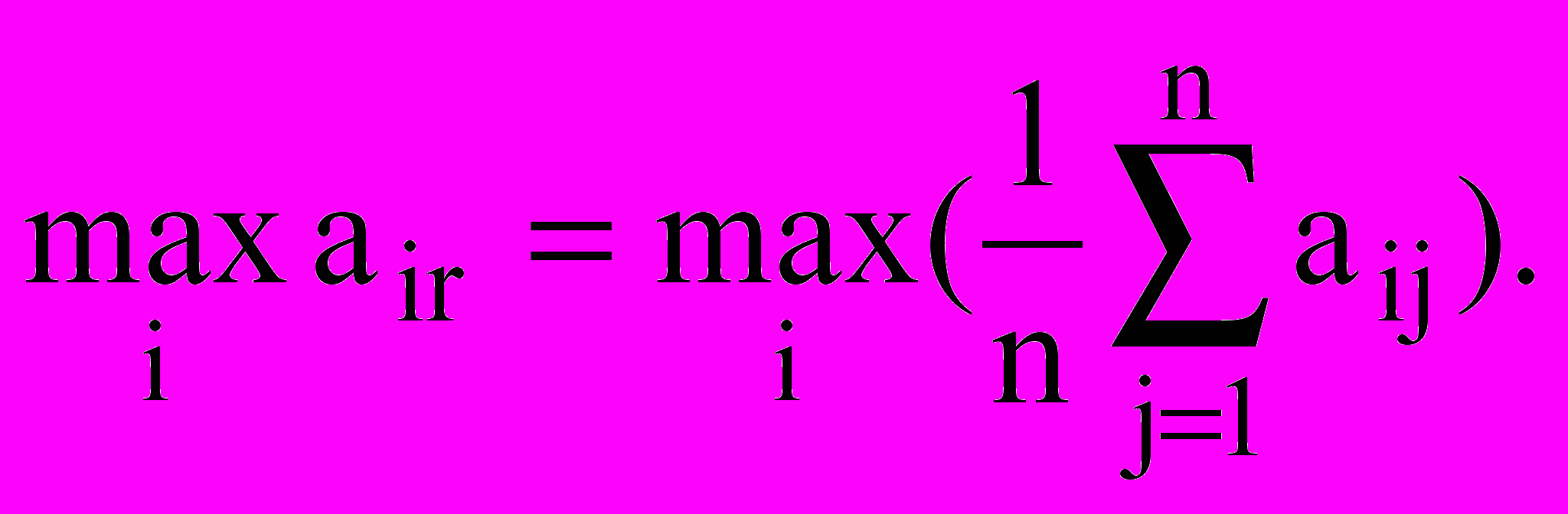(2)

Конструктор исходит из того, что все встречающиеся отклонения результата решения от "среднего" случая допустимы, и выбирает размеры, оптимальные с этой точки зрения.

Имеется ряд критериев, которые используются при выборе оптимальной стратегии. Рассмотрим некоторые из них.

Особые случаи

Схематическое сопоставление всех возможных полезностей a_ij различных решений в матрице табл. 2 облегчает поначалу их обозрение, не требуя при этом формальной оценки. Эта матрица может быть меньшего объёма (табл.8) и даже выродиться в единственный столбец, если будет представлена полная информация о том, с каким внешним состоянием Вj следует считаться. Это соответствует элементарному сравнению различных технических решений. Матрица решений может, однако, свестись и к единственной строке (см. табл.9). В этом случае мы имеем дело с так называемой фатальной ситуацией принятия решений, когда в силу ограничений технического характера, внешних условий и других причин остаётся единственный вариант, хотя его дальнейшие последствия зависят от внешнего состояния Вj, и поэтому результат решения оказывается неизвестным [Мушик Э., Мюллер П. Методы технических решения: Пер. с нем. – М.: Мир, 1990. – 208 с., ил.].

Таблица. 8. Матрица решений (n2)

Условия Варианты	B1	B2
X1	a11	a12
X2	a21	a22
X3
Xi	ai1	ai2
Xn	an1	an2

Таблица.9. Фатальная ситуация в принятии решений

Условия Варианты	B1	B2	B3		Bj		Bm
X1	a11	a12	a13		a1j		a1n

Случается и так, что некоторый вариант решения, например, оказывается настолько удачным, что для другого варианта X_l из матрицы выполняются неравенства a_kj≥a_lj для j=1, …, n. Тогда говорят, что решение X_k доминирует над решением. Решение X_k в этом случае с самого начала оказывается лучшим, а вариант X_l, напротив, с самого начала не представляет далее интереса.