Общеобразовательные программы основного общего образования Выпуск 6
| Вид материала | Отчет |
Содержание3. Общая оценка результатов выполнения работы Распределение количества выпускников по общему баллу Сместиться на (–3, 2) Команда1 Команда2 Команда3 Пример работы программы |
- Основная образовательная программа начального общего образования на 2011-2015 уч годы, 9656.88kb.
- Еждений, реализующих общеобразовательные программы начального общего, основного общего, 497.29kb.
- Перечень актуальных тем авторских разработок, 69.39kb.
- «Согласовано» «Утверждаю» Председатель Управляющего Совета: Директор школы, 1022.45kb.
- Рабочая программа составлена на основе Федерального компонента Государственного стандарта, 394.72kb.
- Правительства Российской Федерации от 9 февраля 2010 года № 64, Правилами проведения, 309.58kb.
- Программа основного общего образования Биология 5-9 классы. Линейный курс, 1195.68kb.
- Доклад по итогам работы моу «Средняя общеобразовательная школа №29», 301.11kb.
- Реализующем общеобразовательные программы начального общего, основного общего, среднего, 1533.06kb.
- Презентация результатов профессиональной деятельности учителей образовательных учреждений,, 200.27kb.
3. Общая оценка результатов выполнения работы
Для оценивания результатов выполнения работы учащимися применялись два количественных показателя: традиционная отметка и общий балл. Максимальный общий балл, который можно было получить за выполнение всех заданий экзаменационной работы – 26. Общий балл формируется путем суммирования баллов, полученных учащимися за выполнение всех заданий экзаменационной работы. За выполнение всех заданий базового уровня учащийся мог получить 13 баллов. Выполнение всех заданий повышенного уровня добавляет еще 8 баллов, итого 21 балл. За каждое выполненное задание высокого уровня добавляется по 2 балла. Итого 26 баллов.
Диаграмма 2.
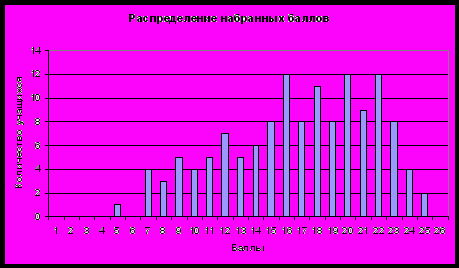
Анализ диаграммы 2 позволяет увидеть, что максимальный балл (26) не набрал ни один участник экзамена, 25 баллов набрали 2 ученика (1,5%).
Среднеобластной балл составляет 16,8; набрали балл выше среднеобластного 74 (55,2 %) учащихся.
Распределение количества выпускников по общему баллу
Таблица 5.
| Баллы | Количество учащихся, набравших данный балл (%) |
| 0 - 13 | 25,4 |
| 14 - 21 | 55,2 |
| 22 - 26 | 19,4 |
Анализ таблицы 5 показывает, что большая часть участников экзамена (74,6%) справились с заданиями базового уровня, а также с частью заданий повышенного уровня сложности. С заданиями высокого уровня сложности которые выполнялись с использованием компьютера, справились 23,5% участников экзамена.
Приведем примеры некоторых заданий, которые вызвали наибольшие затруднения у учащихся:
| Обозначение заданий в работе, номер варианта работы | Содержание задания | Средний показатель выполнения, % | |||||||||||||||||||||||||||
| 8 № 1112 | Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду Сместиться на (a, b) (где a, b – целые числа), перемещающую Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Если числа a, b положительные, значение соответствующей координаты увеличивается, если отрицательные – уменьшается. Например, если Чертёжник находится в точке с координатами (9, 5), то команда Сместиться на (–3, 2) переместит Чертёжника в точку (6, 7). Запись Повтори k раз Команда1 Команда2 Команда3 конец означает, что последовательность команд Команда1 Команда2 Команда3 повторится k раз. Чертёжнику был дан для исполнения следующий алгоритм: Повтори 3 раз Сместиться на (1, –3) Сместиться на (–4, 1) Сместиться на (1, 1) конец На какую одну команду можно заменить этот алгоритм, чтобы Чертёжник оказался в той же точке, что и после выполнения алгоритма? 1) Сместиться на (–6, –3) 2) Сместиться на (6, 3) 3) Сместиться на (–2, –1) 4) Сместиться на (6, –3) | 37,5 | |||||||||||||||||||||||||||
| 13 № 1112 | Переведите десятичное число 201 в двоичную систему счисления. | 45,8 | |||||||||||||||||||||||||||
| 14 № 1112 | Дан фрагмент электронной таблицы, в которой символ «$» используется для обозначения абсолютной адресации:
Формулу, записанную в ячейке E2, скопировали в буфер обмена и вставили в ячейку D1, при этом изменились относительные ссылки, использованные в формуле. Определите значение формулы, которая окажется в ячейке D1. В ответе укажите одно число – значение формулы.
| 29,2 | |||||||||||||||||||||||||||
| 23.2 №1109 | Напишите программу для решения следующей задачи. Девятиклассники участвовали в викторине по математике. Необходимо было ответить на 20 вопросов. Победителем викторины считается участник, правильно ответивший на наибольшее количество вопросов. На сколько вопросов победитель ответил правильно? Если есть участники викторины, которые не смогли дать правильный ответ ни на один из вопросов, выведите YES, иначе выведите NO. Гарантируется, что есть участники, правильно ответившие хотя бы на один из вопросов. Программа получает на вход число участников викторины N (1 ≤ N ≤ 50), затем для каждого участника вводится количество вопросов, на которые получен правильный ответ. Пример работы программы:
| 8,7 |
