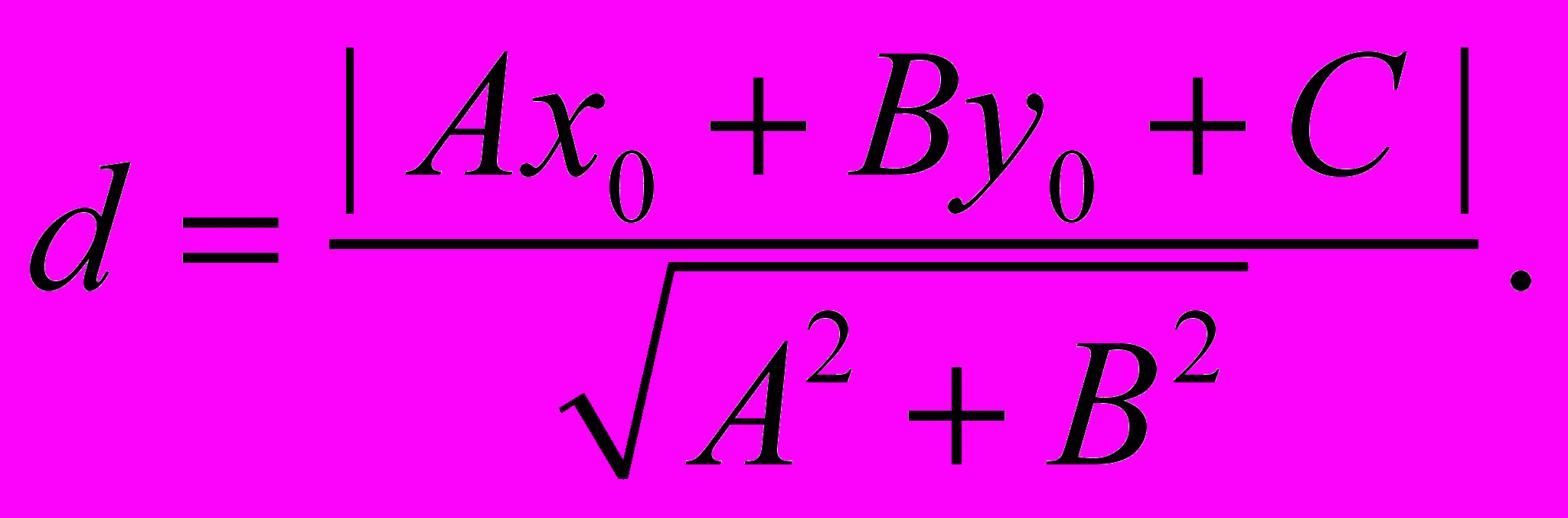Лекция №8

Вид материала

Лекция

Содержание M принадлежит множеству Γ тогда и только тогда, когда n M0 и перпендикулярную вектору n 2.1.2. Условия параллельности и перпендикулярности 2.1.3. Расстояние от точки до плоскости

Подобный материал:

• «Социальная стратификация и социальная мобильность», 46.19kb.
• Первая лекция. Введение 6 Вторая лекция, 30.95kb.
• Лекция Сионизм в оценке Торы Лекция Государство Израиль испытание на прочность, 2876.59kb.
• Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
• Собрание 8-511 13. 20 Лекция 2ч режимы работы эл оборудования Пушков ап 8-511 (ррэо), 73.36kb.
• Концепция тренажера уровня установки. Требования к тренажеру (лекция 3, стр. 2-5), 34.9kb.
• Лекция по физической культуре (15. 02.; 22. 02; 01. 03), Лекция по современным технологиям, 31.38kb.
• Тема Лекция, 34.13kb.
• Лекция посвящена определению термина «транскриптом», 219.05kb.
• А. И. Мицкевич Догматика Оглавление Введение Лекция, 2083.65kb.

Лекция № 8 (20.10.09)


Глава 2. Линейные уравнения на плоскости и в пространстве


§ 2.1. Прямая линия на плоскости и плоскость в пространстве


2.1.1. Основная теорема

Рассмотрим общий вид линейного уравнения (т. е. уравнения первой степени) в трёхмерном пространстве:

Ax + By + Cz + D = 0 (1)

и на плоскости:

Ax + By + C = 0. (2)

Обозначим через n вектор {A; B; C} (в двумерном случае {A; B}).

Основная теорема. Если n ≠ 0, то уравнение (1) является уравнением плоскости, а уравнение (2) − прямой линии. При этом вектор n ортогонален этой плоскости или пря­мой.

Доказательство буду вести для трёхмерного случая, для двумерного рассуждение аналогично.

Обозначим через Γ множество всех тех и только тех точек пространства, коорди­наты которых удовлетворяют уравнению (1). Нам надо доказать, что Γ есть плоскость, перпендикулярная n.

Убедимся прежде всего, что множество Γ непусто. Хотя бы одно из чисел A, B и C не равно 0. Пусть, например, B ≠ 0. (Для других случаев рассуждение аналогично.) Будем искать точку (x₀; y₀; z₀), удовлетворяющую уравнению (1) и дополнительным условиям x₀ = 0 и z₀ = 0. Получаем уравнение

By₀ + D = 0,

которое имеет (единственное) решение 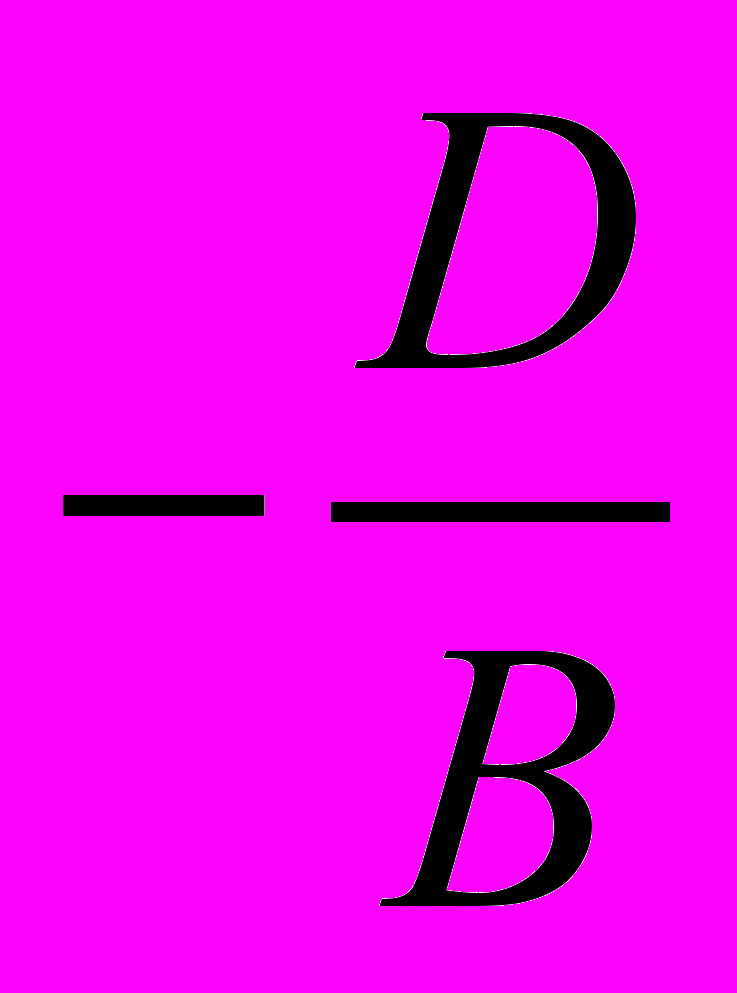, потому что B ≠ 0. Следовательно, точка (0; 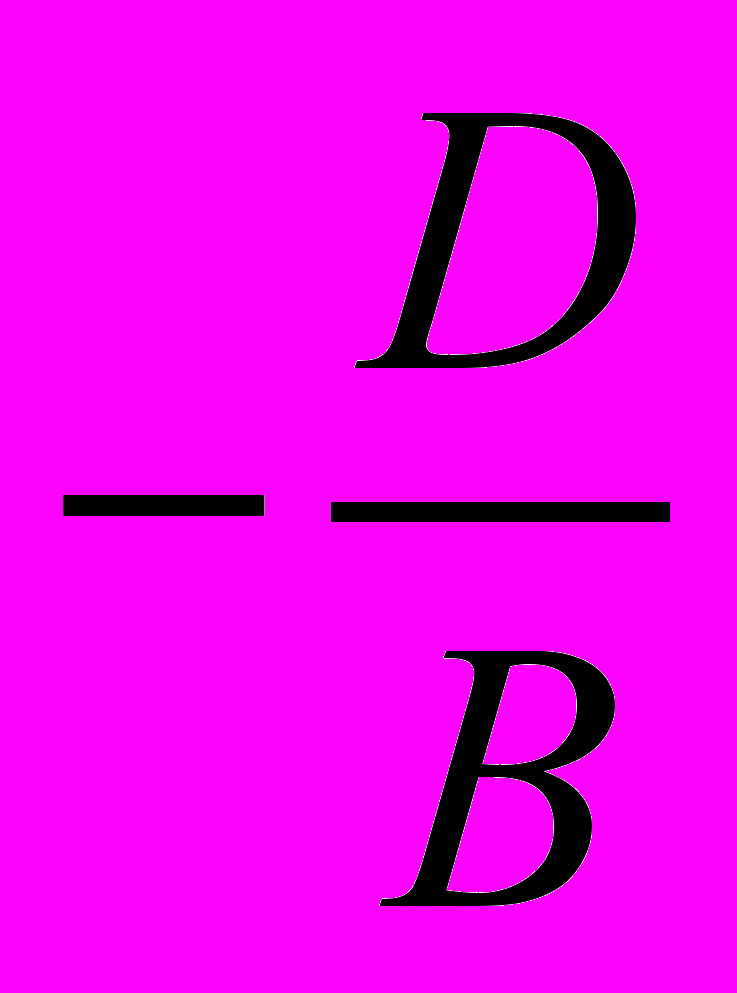; 0)  Γ и Γ непусто. Возьмём и зафиксируем теперь какую-нибудь точку, принадлежа­щую Γ (они есть), и обозначим её через M₀. Пусть её координаты суть (x₀; y₀; z₀). Так как эта точка принадлежит Γ, для её координат справедливо соотношение:

Ax₀ + By₀ + Cz₀ + D = 0. (1)

Вычитая из уравнения (1) равенство (1), мы получаем новое уравнение

A(x − x₀) + B(y − y₀) + C(z − z₀) = 0, (1*)

очевидным образом равносильное уравнению (1) (т. к. мы можем вернуться к уравнению (1), прибавляя к уравнению (1*) равенство (1)). Значит, уравнение (1*) определяет то же самое множество Γ.


Возьмём теперь произвольную точку M = (x; y; z) из множества Γ и распишем ко­ординаты вектора :

{ x − x₀; y − y₀; z − z₀}.

Уравнение (1*) можно записать теперь так:

(n, ) = 0. (3)

Это новое равенство (3) показывает нам, что точка ^ M принадлежит множеству Γ тогда и только тогда, когда n  . Обозначим через π плоскость, проходящую через точку ^ M₀ и перпендикулярную вектору n. Если точка M принадлежит множеству Γ, то n  . Прямая M₀M перпендикулярна вектору n и, следовательно, лежит в π. Значит, точка M лежит в π. Но, очевидно, верно и обратное, так что Γ = π, QED.

Следствие из теоремы. Уравнение плоскости, проходящей через точку с координа­тами (x₀; y₀; z₀) и ортогональной данному ненулевому вектору с координатами {A; B; C}, имеет вид:

A(x − x₀) + B(y − y₀) + C(z − z₀) = 0

(в двумерном случае уравнение прямой, проходящей через точку с координатами (x₀; y₀) и ортогональной данному ненулевому вектору с координатами {A; B}, есть A(x − x₀) + B(y − − y₀) = 0).

Примечания. 1. Заметим, что выполнение неравенства n ≠ 0 в условии теоремы существенно, ибо если n = 0, то в трёхмерном случае мы получим либо пустое множество (если D ≠ 0), либо всё пространство (если D = 0). Равным образом в двумерном случае по­лучим либо пустое множество (если C ≠ 0), либо всю плоскость (если C = 0).

2. Верно и обратное утверждение: любая плоскость в трёхмерном пространстве об­ладает уравнением вида (1), а любая прямая на плоскости − уравнением вида (2).

Доказательство (для трёхмерного случая). Возьмём произвольный вектор n = {A; B; C} ≠ 0, ортогональный данной плоскости, и произвольную точку M₀ = (x₀; y₀; z₀), ей принадлежащую. Рассмотрим уравнение (1*). По основной теореме оно определяет плос­кость, перпендикулярную вектору n. Очевидно также, что эта плоскость проходит через точку M₀. Но такая плоскость единственна и совпадает с данной.

Определение. Уравнения (1) и (2) называются общими уравнениями соответст­венно плоскости и прямой.


^ 2.1.2. Условия параллельности и перпендикулярности

1. Условие компланарности двух плоскостей

Пусть даны две плоскости:

A₁x + B₁y + C₁z + D₁ = 0, n₁ = {A₁; B₁; C₁} ≠ 0; (1)

A₂x + B₂y + C₂z + D₂ = 0, n₂ = {A₂; B₂; C₂} ≠ 0. (2)

Когда они компланарны (т. е. параллельны или совпадают)? Очевидно, это будет тогда и только тогда, когда их нормальные векторы коллинеарны. Применяя критерий компла­нарности, получаем

Предложение 1. Две плоскости компланарны тогда и только тогда, когда вектор­ное произведение их нормальных векторов равно нулевому вектору:

[n₁, n₂] = 0.


2. Условие совпадения двух плоскостей

Предложение 2. Плоскости (1) и (2) совпадают тогда и только тогда, когда все че­тыре их коэффициента пропорциональны, т. е. существует такое число λ, что

A₂ = λA₁, B₂ = λB₁, C₂ = λC₁, D₂ = λD₁. (3)

Доказательство. Пусть условия (3) выполнены. Тогда уравнение второй плоскости может быть записано так:

λA₁x + λB₁y + λC₁z + λD₁ = 0.

λ ≠ 0, иначе было бы A₂ = B₂ = C₂ = D₂ = 0, что противоречит условию n₂ ≠ 0. Следова­тельно, последнее уравнение эквивалентно уравнению (1), а это означает, что две плоско­сти совпадают.

Пусть теперь, наоборот, известно, что данные плоскости совпадают. Тогда их нор­мальные векторы коллинеарны, т. е. существует такое число λ такое, что

A₂ = λA₁, B₂ = λB₁, C₂ = λC₁.

Уравнение (2) можно теперь переписать в виде:

λA₁x + λB₁y + λC₁z + D₂ = 0.

Умножим уравнение (1) на λ, получим равносильное уравнение первой плоскости (т. к. λ ≠ 0):

λA₁x + λB₁y + λC₁z + λD₁ = 0.

Возьмём какую-нибудь точку (x₀, y₀, z₀) из первой (а следовательно, и второй) плоскости и подставим её координаты в последние два уравнения; получим верные равен­ства:

λA₁x₀ + λB₁y₀ + λC₁z₀ + D₂ = 0 ;

λA₁x₀ + λB₁y₀ + λC₁z₀ + λD₁ = 0.

Вычитая из верхнего нижнее, получим D₂ − λD₁ = 0, т. е. D₂ = λD₁, QED.

3. Условие перпендикулярности двух плоскостей

Очевидно, для этого необходимо и достаточно, чтобы нормальные векторы были перпендикулярны.

Предложение 3. Две плоскости перпендикулярны тогда и только тогда, когда ска­лярное произведение нормальных векторов равно нулю:

(n₁, n₂) = 0.


^ 2.1.3. Расстояние от точки до плоскости

Пусть дано уравнение плоскости

Ax + By + Cz + D = 0, n = {A; B; C} ≠ 0,

и точка M₀ = (x₀, y₀, z₀). Выведем формулу расстояния от точки до плоскости:



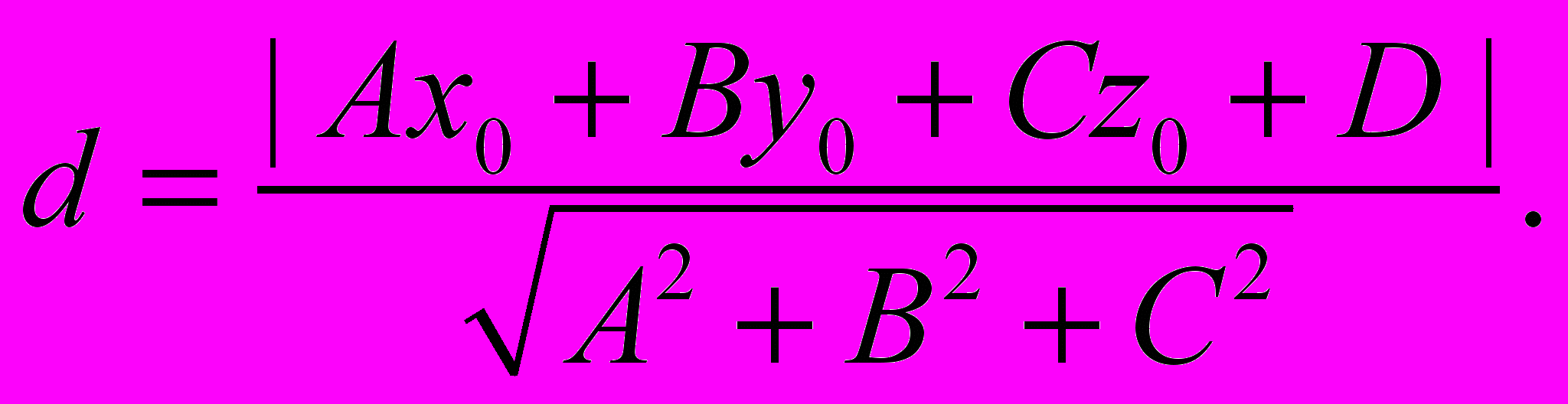
Возьмём произвольную точку Q = (x₁, y₁, z₁), лежащую в данной плоскости. Её ко­ординаты удовлетворяют уравнению плоскости:


Ax₁ + By₁ + Cz₁ + D = 0.

Заметим теперь, что искомое расстояние d равно абсолютной величине проекции вектора на направление вектора n (здесь мы берём проекцию как числовую величину, а не как вектор). Далее применяем формулу для вычисления проекции:





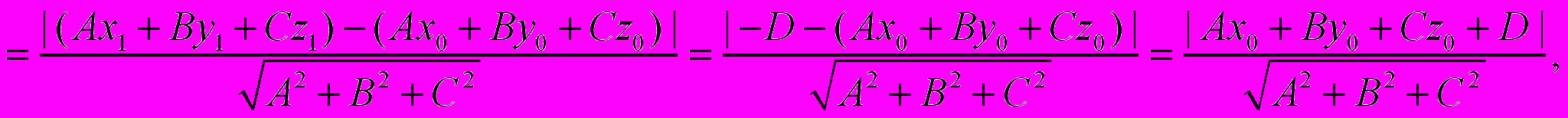
QED.

Аналогичная формула справедлива для расстояния d от точки M₀ = (x₀, y₀) плоско­сти до прямой, заданной общим уравнением Ax + By + C = 0: