Программа предрофильного элективного курса по математике для классов естественно-математического цикла

Вид материала

Программа

Подобный материал:

• Программа элективного курса по математике для учащихся 10 11 классов (68 часов, 2 года,, 118.36kb.
• Программа элективного курса «Аналитическая химия», 224.89kb.
• Предлагаемый курс направлен на интеграцию знаний учащихся естественно-научного цикла, 119.13kb.
• Программа элективного курса «Измерение физических величин» ( 34 часа), 128.64kb.
• Программа элективного курса по химии химия в промышленности, 943.59kb.
• Программа составлена на основе программы элективного курса для учащихся 9-х классов, 200.18kb.
• Программа составлена специально для изучения отдельных разделов математики в классах, 36.16kb.
• Разработаны программы элективных курсов. Программа элективного курса по математике, 98.58kb.
• Отчет мо учителей естественно-математического цикла, 36.42kb.
• Программа элективного курса Ставрополь, 186.92kb.

Программа предрофильного элективного курса по математике для классов естественно-математического цикла.


9 класс


Уравнения и неравенства с переменной под знаком модуля.

Пояснительная записка


Решение задач, связанные с модулями в школьной программе встречается очень мало. При сдаче ЕГЭ и при поступлении, особенно в технические вузы, обязательно встречаются задания, где требуются знания по решению нестандартных задач с модулями.

Моя программа предусматривает углубление знаний по решению уравнений, неравенств и задач с применением модуля.

Курс способен вызвать большой интерес к изучаемой теме, на многочисленных примерах показать различные способы решения задач. Применение проблемного обучения позволит сделать занятия интересными и эффективными.

Программа рассчитана на 18 часов.


Цель программы:


- Ознакомить учащихся с основными методами решения уравнений и неравенств с модулями.

- Дать возможность школьникам развивать свои способности, в том числе развитие памяти.


Задачи программы:


- Научить решать линейные уравнения и неравенства различными способами.

- Научить решать квадратные уравнения различными способами.

- Развитие логического мышления, знаний, умений и навыков при обучении решения нестандартных задач с модулями.

- Формировать навыки исследовательской работы.


Содержание программы:

Тема1. Решение уравнений.

Рассматривается определение модуля, геометрический смысл. Решаются линейные, квадратные, дробно-рациональные уравнения с переменной под знаком модуля. Исследуется многообразный метод решения.


Тема2. Уравнение, решение которых основано на свойствах модуля.

П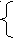рименяем следующие свойства:

1) |a| + |b| = a + b <=> a ≥ 0

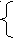b ≥ 0

2) |a| + |b| = a - b <=> a ≥ 0

b ≤ 0

3) |a + b| = |a| + |b| <=> ab ≥ 0

4) |a - b| = |a| + |b| <=> ab ≤ 0


Тема3. Графическое решение уравнений.

Исследуются различные способы построения графиков функций, содержащих модуль. Особое внимание будет уделено решению уравнений, содержащих параметр.


Тема4. Решение неравенств.

Основным методом решения неравенств со знаком модуля является тот же метод, что и при решении уравнений. Кроме этого используем:

1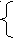. |f(x)| < g(x) <=>

f(x) < g(x)

f(x) > -g(x)

2. |f(x)| > g(x) <=> f(x) > g(x)

f(x) > -g(x)

3. |f(x)| < |g(x)|

Тема5. Подведение итога контрольная работа на два варианта.


Тематическое планирование

№	Тема занятия	Кол-во часов	Виды деятельности	Форма контроля
1	Решение уравнений вида f(|x|) = g(x) |f(|x|)| = g(x) |f1(x)| + |f2(x)| + …+|fn(x)|= g(x)	1 ч. 2 ч. 2 ч. 1 ч.	Лекция Решение примеров	тестирование
2	Уравнения, решение которых основано на свойствах модуля.	4 ч.	Лекция Решение задач	Самостоятельная работа
3	Графическое решение уравнений, содержащих модуль	2 ч.	Лекция Решение задач	Групповая работа
4	Решение неравенств, содержащих переменную под знаком модуля	3 ч.	Лекция Решение задач	Групповая работа
5	Подведение итогов	2 ч.		Контрольная работа

Литература:

1. И.В. Пархимович, Минск ,Высшая школа 1998г.
   
2. В.Вавилов «Задачи по математике»М, Наука 1987г.
   
3. А.И.Азаров «Алгебраические уравнения и неравенства» Минск, Высшая школа 1997
   
4. Е.М.Родионов «Пособие для поступающих в вузы» М, 2005г.