Geum.ru

Программа междисциплинарного вступительного экзамена в магистратуру по направлению «математика»

Вид материалаПрограмма

Содержание


По алгебре
Подобный материал:


ПРОГРАММА МЕЖДИСЦИПЛИНАРНОГО ВСТУПИТЕЛЬНОГО ЭКЗАМЕНА

В МАГИСТРАТУРУ ПО НАПРАВЛЕНИЮ «МАТЕМАТИКА»


  1. Алгебра. Линейная алгебра и геометрия

Комплексные числа. Алгебраическая и тригонометрическая формы записи комплексного числа. Операции над комплексными числами. Модуль и аргумент комплексного числа. Возведение в степень и извлечение корней из комплексных чисел.

Линейное пространство. Подпространство. Линейно зависимые и линейно независимые системы векторов. Базис и размерность. Координаты вектора и матрица перехода. Линейные отображения и матрицы, собственные числа и векторы, характеристический многочлен. Вещественное евклидовое пространство. Скалярное произведение векторов и его свойства. Неравенство Коши–Буняковского. Длина вектора и угол между векторами. Ортогональные и ортонормированные базисы. Процесс ортогонализации.

Операции над матрицами. Ранг матрицы. Обратимые матрицы. Определитель квадратной матрицы и его разложение по строке или столбцу.

Системы линейных алгебраических уравнений. Пространство решений однородной системы, его размерность и базис, общее решение. Критерий существования ненулевого решения однородной системы. Неоднородные системы, частное и общее решения.

Многочлены от одной переменной с комплексными коэффициентами. Операции над многочленами. Корень многочлена, простые и кратные корни. Теорема Безу. Основная теорема алгебры. Случай многочленов нечетных степеней с вещественными коэффициентами.

Вещественные квадратичные формы. Канонический вид. Определенные и неопределенные квадратичные формы. Закон инерции для вещественных квадратичных форм.


Вопросы к экзамену:
  1. Критерий обратимости матрицы и формула для обратной матрицы.
  2. Преобразование координат вектора при переходе от одного базиса к другому.
  3. Критерий совместности системы линейных алгебраических уравнений (теорема Кронекера-Капелли).
  4. Разложение многочленов с комплексными и вещественными коэффициентами. Формулы Виета.
  5. Закон инерции вещественных квадратичных форм.
  6. Собственные числа и собственные векторы матрицы и их свойства
  7. Теорема Гамильтона – Кели.



  1. Математический анализ.

Действительные числа. Аксиоматика множества действительных чисел. Последовательность в Rn , n≥1, ограниченные и неограниченные последовательности в Rn. Предел, частичный предел, предел последовательности в Rn. Их существование и свойства. Сходящиеся и расходящиеся последовательности в R1. Верхний, нижний предел последовательности в R1. Теорема о пределе монотонной последовательности. Способы вычисления пределов последовательности в R1 и в Rn , n≥2. Примеры вычисления пределов последовательности .

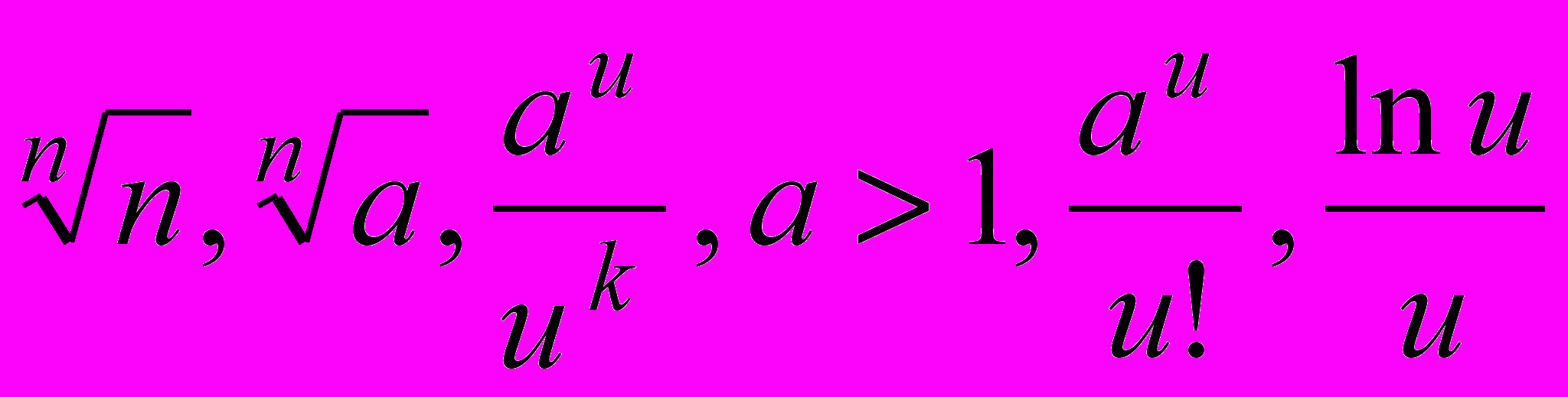Функция f: Rn →Y(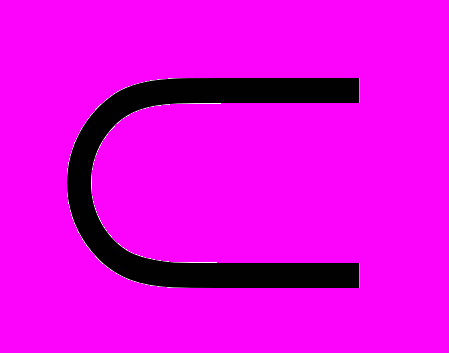R). Понятие инъективной, сюръективной, биективной функции. Определение предела функции в точке на языке «ε-N» и языке последовательностей (теорема Гейне). Определение непрерывной в точке функции на языке «ε-N» и языке пределов. Локальные свойства функции, имеющих в точке конечный предел: единственность предела, локальная ограниченность. Определение непрерывной на множестве функций. Понятие монотонной функции. Теорема о пределе монотонной на (a,b) функции. Понятие компакта в Rn . Свойства непрерывных на компакте функции : I и II теоремы Вейерштрасса, теорема Кантора. Дифференцируемость в точке ф.м.п. f: Rn → R, ее производная и дифференциал в точке. Связь между дифференцируемыми и непрерывными в точке функциями. Свойства дифференцируемых на промежутке функций: теоремы Ферма, Ролля, Коши, Лагранжа о конечном приращении. Понятие монотонной функции. Достаточные условия монотонности функции на промежутке. Правило Лопиталя, раскрытие неопределенности при вычислении предела функции. Дифференцируемость в точке ф.м.п. f: Rn → R и отображения f: Rn → Rn. Частная производная и дифференциал в точке функций многих переменных. Необходимые и достаточные условия дифференцируемости ф.м.п. в точке. Понятие непрерывной дифференцируемости ф.м.п. и отображения в точке. Теорема о дифференцируемости суперпозиции. Теорема о совпадении смешанных производных.

Определение неопределенного интеграла.Определение интеграла Римана (определенного интеграла) от функции на отрезке П =[a,b] в R1 и параллелепипеде П в Rn. Необходимое условие интегрируемости функции по Риману. Суммы Дарбу и критерии Дарбу интегрируемости функции на П. Свойство аддитивности интеграла Римана с переменным верхним пределом. Его свойства. Множество, измеримое по Жордану в Rn, его мера. Жордановы нуль -множества и их свойства. Определение функции, интегрируемой по Риману на Жордановом множестве. Формула Ньютона –Лейбница для интеграла Римана по отрезку. Метод сведения интеграла Римана по параллелепипеду П в Rn, n-кратного интеграла к повторным, теорема Фубини.

Определение несобственного интеграла с единственной особой точкой, его сходимость. Признаки сходимости несобственных интегралов от неотрицательных функций. Абсолютная и условная сходимость несобственных интегралов с одной особой точкой. Определение сходимости несобственного интеграла с конечным числом особых точек, корректность определения, его абсолютная и условная сходимость. Определение несобственного интеграла, зависящего от параметра. Поточечная и равномерная сходимость несобственного интеграла, зависящего от параметра на множестве. Признак Вейерштрасса равномерной сходимости. Примеры Г-функций и В-функций Эйлера.

Числовой ряд. Его сходимость (расходимость). Признаки сравнения Коши, Даламбера, сходимости рядов с неотрицательным общим членом. Определение абсолютно и условно сходящихся рядов. Свойства сходящихся рядов: теорема об арифметических операциях, переместительное свойство, сочетательное свойств. Знакопеременные ряды, признак Лейбница.

Понятие функционального ряда {fn(x)}, fn : R1 → R1. Поточечная и равномерная сходимость функционального ряда на множестве. Признак Вейерштрасса равномерной сходимости. Понятие ряда Фурье от функции, определенной на [-π;π] по классической тригонометрической системе. Коэффициенты Фурье. Разложение функций в ряды Фурье только по sin или cos кратных дуг.


Вопросы к экзамену:
  1. Теорема об ограниченности непрерывной на отрезке вещественной функции одной переменной
  2. Теорема о необходимом и достаточном условии дифференцируемости вещественнозначной функции одной переменной .
  3. Теорема о непрерывности и дифференцируемости интеграла с переменным верхним пределом.
  4. Теорема о сходимости абсолютно сходящего несобственного интеграла.
  5. Теорема Лейбница о сходимости знакочередующегося числового ряда.
  6. Формула Грина как основная формула анализа.
  7. Признак Вейерштрасса равномерной сходимости функционального ряда.



  1. ТФКП.

Дифференцируемость функции комплексного переменного. Аналитические функции. Интегрирование ф.к.п. Сведение интеграла к криволинейным интегралам 1,2 рода. Интегральная теорема Коши. Интегральная формула Коши для простого и сложного контуров. Интеграл типа Коши. Теорема Морера. Принцип максимальности модуля. Лемма Шварца. Теорема единственности.

Степенной ряд, круг и радиус сходимости. Теорема Абеля. Примеры разложения в степенной ряд функций: еz, sin z, cos z, ln(1+z), (1+z)μ, sh z, chz .

Понятие изолированной особой точки однозначного характера для аналитической функции (и.о.т.о.х). Критерий устранимой и.о.т.о.х, полюса, существенно особой точки . Теорема Сохоцкого. Ряд Лорана функции, теоремы о вычетах. Применение теории вычетов к вычислению определенных интегралов типа: , , .


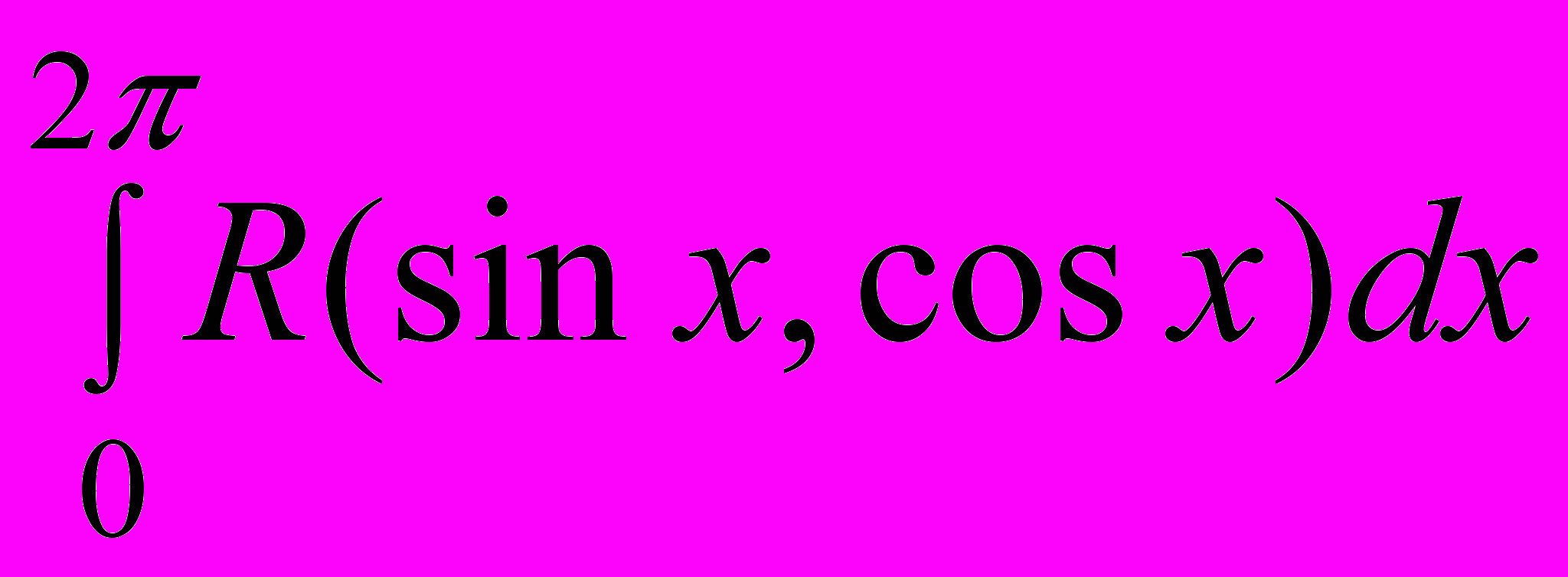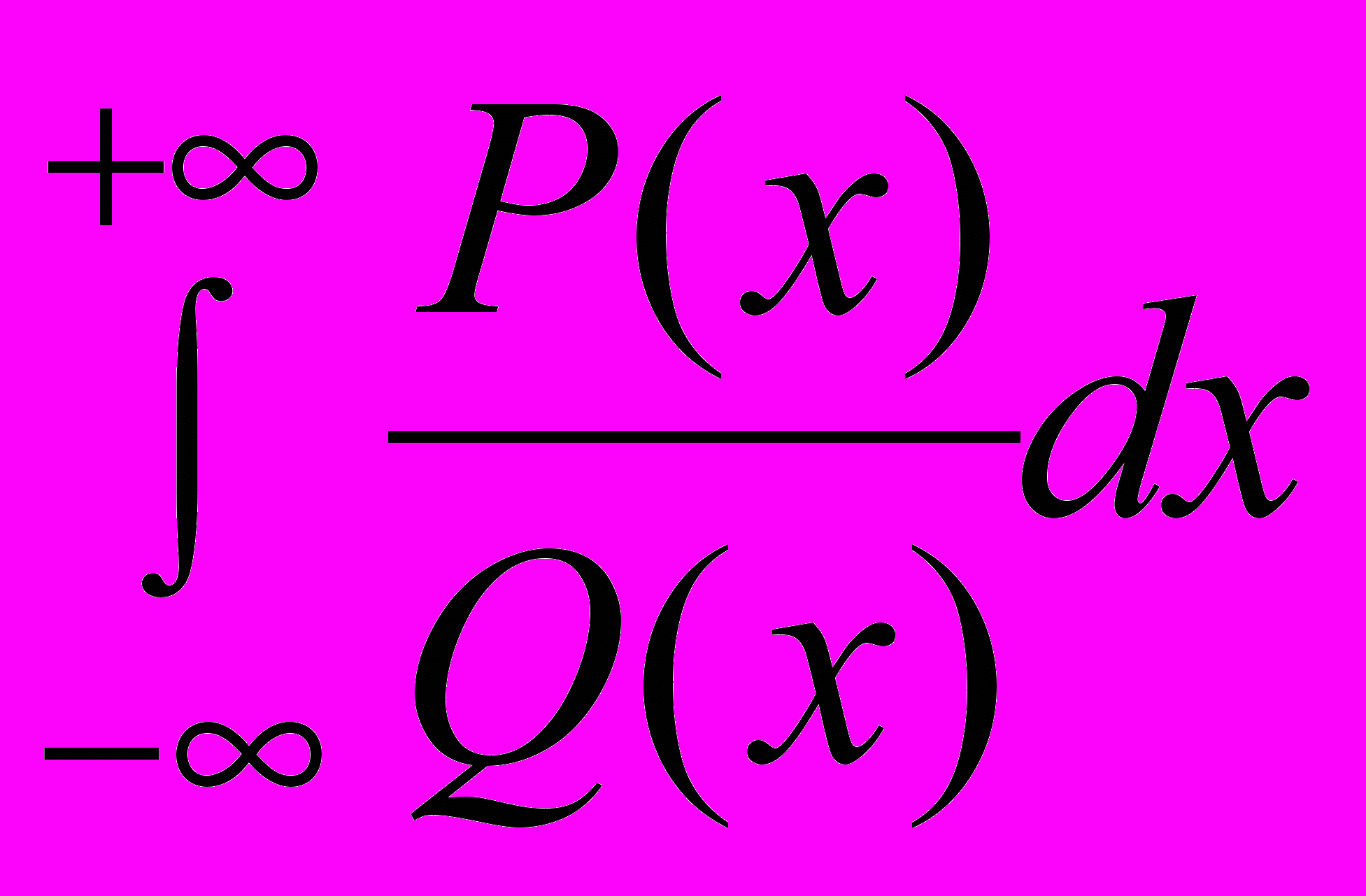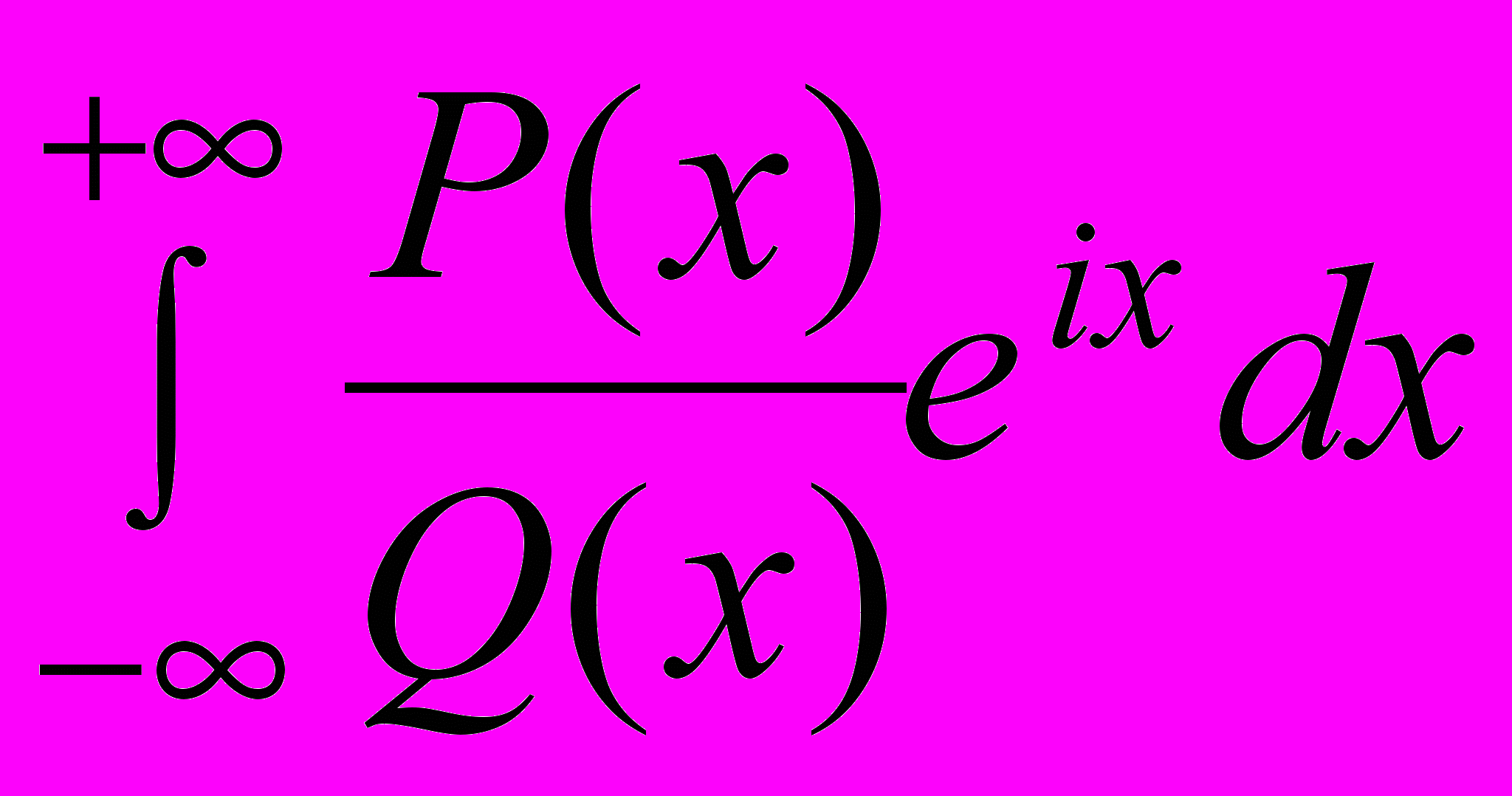Дробно-линейная функция (д.л.ф.), как пример функции, отображающей конформно расширенную комплексную плоскость на себя. Основные свойства д.л.ф. Элементарные функции 1/2 (z+1/z). Примеры конформного отображения областей элементарными функциями. Многозначные функции z1/n, Ln z, Arcsin z, Arctg z. Понятие об аналитическом продолжении.


Вопросы к экзамену:

Дробно-линейная функция, и конформные отображения.
  1. Интегральная формула Коши для простого и сложного контуров.
  2. Разложение аналитической функции в ряд Лорана.
  3. Теоремы о вычетах.


4. Функциональный анализ и интегральные уравнения.

Понятие о мощности множества. Свойства счетных множеств. Множества мощности континуума. Примеры счетных множеств и множеств мощности континуума. Определение метрического пространства. Примеры:Rn, Cn,, m, c, S, l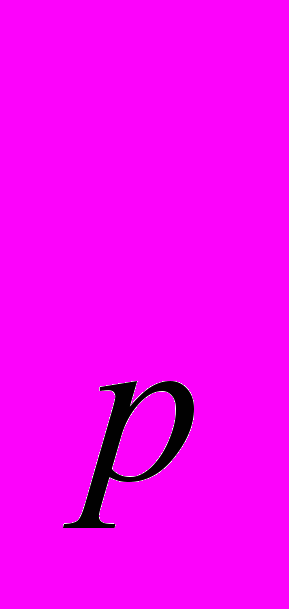, С[a,b], L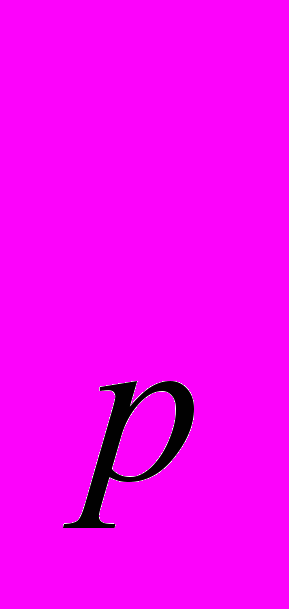[a,b]. Сходящиеся последовательности элементов метрического пространства, их свойства. Открытые и замкнутые в метрическом пространстве множества. Всюду плотные и нигде не плотные множества. Фундаментальные последовательности. Полные метрические пространства. Примеры полных и неполных пространств. Тоерма Бэра. Теорема о вложенных шарах. Меры на кольцах и алгебрах. Мера Лебега и ее свойства. Мера Лебега – Стилтьеса. Измеримые функции и их свойства. Сходимость почти всюду и сходимость по мере. Теорема Егорова. Теоремы Лебега и Рисса о сравнении сходимости почти всюду и по мере.

Интеграл Лебега от простой функции. Интеграл Лебега от произвольной измеримой функции. Свойства интеграла Лебега . Полная аддитивность и абсолютная непрерывность интеграла Лебега. Теоремы Лебега, Леви, Фату о предельном переходе под знаком интеграла Лебега.

Примеры сепарабельных и несепарабельных метрических пространств. Сепарабельные метрические пространства.

Компактные и предкомпактные множества в метрических пространствах, их свойства. Критерий компактности Хаусдорфа. Критерий компактности в Rn, Cn,, m, c, S, l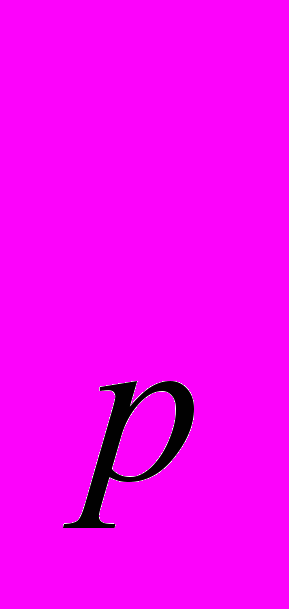, С[a,b], L.

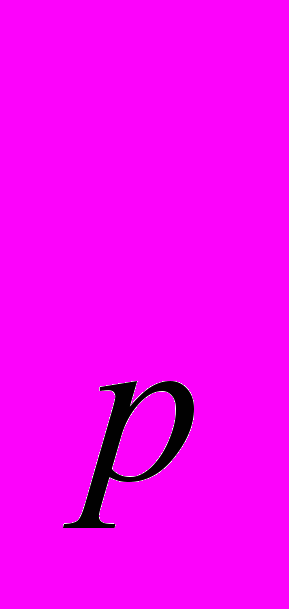Нормированные пространства. Банаховые пространства. Примеры. Непрерывность линейных операций и нормы. Ряды в нормированных пространствах, сходимость и абсолютная сходимость, связь с полнотой пространства. Базис Шаудера. Фактор –пространства. Линейные непрерывные операторы в банаховых пространствах. Примеры непрерывных операторов. Норма оператора. Теорема Банаха –Штейнгауза (принцип равномерной ограниченности). Обратимые операторы. Теоремы о существовании обратных операторов.

Линейные непрерывные функционалы. Общий вид линейного непрерывного функционала в пространствах Rn, Cn,, m, c, S, l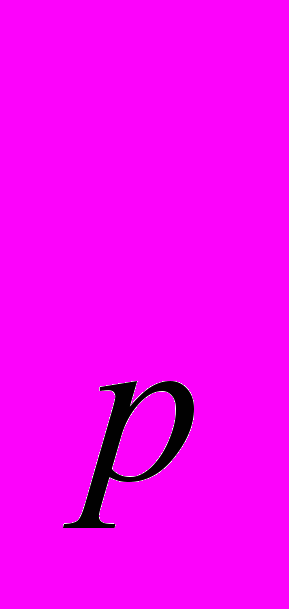, С[a,b], L.

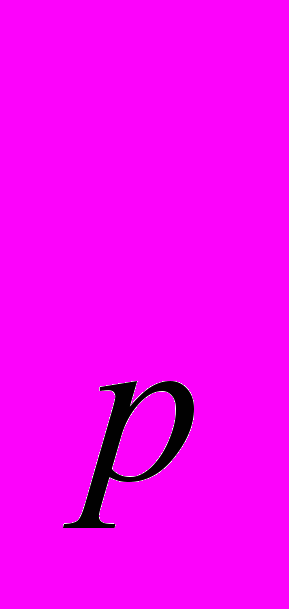Теорема Хана - Банаха. Сопряженные пространства. Рефлексивные пространства. Евклидовы и унитарные пространства. Гильбертовы пространства. Примеры.

Ортогональность. Теорема об ортогональном разложении гильбертова пространства. Ортонормированные системы. Процесс ортогонализации Шмидта. Ряды Фурье по ортонормированным системам. Полнота и замкнутость ортонормированных систем. Неравенство Бесселя и равенство Парсеваля. Резольвента и спектр линейного оператора. Точечный непрерывный и остаточный спектр. Ограниченность, замкнутость и непустота спектра. Спектральный радиус. Тождество Гильберта. Спектр сопряженного оператора.

Компактные операторы. Примеры. Свойства компактных операторов. Компактность интегрального оператора в С[a:b]. Спектр компактного оператора.

Вопросы к экзамену:
  1. Принцип сжимающих отображений и его приложения
  2. Теорема Хана-Банаха (для случая сепарабельного вещественного линейного нормированного пространства).


5. Аналитическая геометрия. Дифференциальная геометрия.

Преобразование декартовой прямоугольной системы координат на плоскости и в пространстве. Общее уравнение прямой на плоскости. Условие параллельности и ортогональности прямых. Канонические уравнения эллипса, гиперболы, параболы.

Общее уравнение плоскости в пространстве. Параметрические уравнения прямой. Условия параллельности и ортогональности прямых и плоскостей. Теорема о вычислении расстояния от точки до плоскости (нормальное уравнение плоскости).

Скалярное, векторное и смешанное произведение векторов пространства и их свойства.

Каноническое уравнение поверхностей второго порядка.

Понятие кривой на плоскости и в пространстве. Кривизна и кручение регулярной кривой. Формула Френе.

Понятие поверхности. Первая и вторая квадратичные формулы поверхности, их применения. Гауссова и средняя кривизна поверхности.


Вопросы к экзамену:
  1. Кривые второго порядка.
  2. Касательная к кривой, длина кривой.
  3. Первая и вторая квадратичные формы поверхности
  4. Средняя и Гауссова кривизна.


6.Дифференциальные уравнения. Уравнения в частных производных.

Теорема существования и единственности Коши-Пикара. Условие полного дифференциала. Понятие об интегрирующем множителе. Однородные линейные дифференциальные уравнения 2-го порядка. Общая теория линейных дифференциальных уравнений n-го порядка (линейная независимость, фундаментальные решения, общее решение). Определение устойчивости, примеры. Лемма и теорема Ляпунова. Системы дифференциальных уравнений. Постановка задачи математической физики. Задача Коши. Краевые задачи. Задача Штурма – Лиувилля. Корректная постановка задачи математической физики. Примеры корректных и некорректных задач. Уравнение теплопроводности, краевые условия. Принцип максимума-минимума решения уравнения теплопроводности, следствия. Гармонические функции. Краевые задачи. Формула Пуассона. Теорема о среднем. Принцип максимума –минимума и его следствия . Определение функции Грина. Задача Дирихле.


Вопросы к экзамену:
  1. Линейное неоднородное дифференциальное уравнение 1 –го порядка и его решение методом Лагранжа.
  2. Построение фундаментальной системы решений линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами.
  3. Решение линейного неоднородного дифференциального уравнения n-го порядка с постоянными коэффициентами (метод квазиполиномов).
  4. Вывод уравнения теплопроводности, граничные условия.
  5. Метод Фурье для решения уравнения колебания струны, закрепленной на концах.


Рекомендуемая литература:
  1. Никольский С.М. Курс математического анализа. Т.1, Т. 2. Москва, Дрофа.2002
  2. Зорич В.А. Математический анализ. Т.1, Т. 2. Москва, Дрофа.2002
  3. Кудрявцев Л.Д. Курс математического анализа. Т.1, 2. Москва, Высшая школа.2001
  4. Ильин В.А., Садовничий В.А., Сендов Б. Математический анализ. Москва, Дрофа.2004

5. Фаддеев Д.К. Лекции по алгебре.- Наука.2001

6. Кострикин А.И. Введение в алгебру.- Наука. 2002

7. Кострикин А.И. Манин Ю.И. Линейная алгебра и геометрия.- Наука.2001
  1. Арнольд В.И. Обыкновенные дифференциальные уравнения .-Москва. Наука. 1971

9. Степанов В.В. Курс дифференциальных уравнений.- Москва. ГИТТЛ.1952

10. Потрягин Л.С. Обыкновенные дифференциальные уравнения.-Москва. Наука. 1974

11.Привалов Н.Н. Введение в теорию функций комплексного переменного

12.Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа.

13.Рашевский П.К. Дифференциальная геометрия


Рекомендуемые задачи:

По математическому анализу: а) Разложение в ряд Маклорена функции: ex, sin x, cos x, (1+x)m, (a+bx)n, ln(1+x), ln(1+x)/(1-x), arctg x;

б) Демидович В.П., Сборник задач и упражнений по математическому анализу: 411,412, 415, 418, 440-443, 474, 482, 512, 514, 517, 687-689, 730, 731,740, 848,852,855,858, 871,875,890,913,917,1040,1048,1064,1091,1269,1270,1289,1299,1319,1398, 1429, 1430,1434, 1435, 1471, 1472, 1674,1675,1680, 1696,1702, 1791,1795, 1798,1866, 1926, 1991, 2207, 2398,2299, 2431, 2556, 2559,2560,2774,3137,3139,3138,3924,3927,4007,4221,4228

^ По алгебре: Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебры. - 5,7,15,36,43, 404, 411, 418,336, 341, 166, 169, 464, 480, 538, 539, 664,

5.Проскуряков И.В. Сборник задач по линейной алгебре. -641, 643, 1175, 1178, 1465,724,728

По дифференциальным уравнениям: .Филиппов А.Ф. Сборник задач по дифференциальным уравнениям: 51-56, 136-146, 186-194, 421-431, 511-532,786-795

По геометрии: Моденов П.С. , Пархоменко А.С. Сборник задач по аналитической геометрии: 152,189,190, 207, 208, 210, 534, 539, 723, 742, 729, 838, 851,

Воднев В.Н. Сборник задач по дифференциальной геометрии: 103, 105, 349, 371, 763, 764, 818, 819