Основные свойства числовых характеристик

Вид материала

Лекции

Подобный материал:

• Урок химии в 9 классе. Тема: «Оксиды азота», 68.76kb.
• Точечные и интервальные оценки статистических числовых характеристик, 73kb.
• Урок №2. Свойства числовых неравенств: Свойство, 16.32kb.
• Основные выводы, 111.66kb.
• Высшая математика с-6,12 (ЭнМИ), 112.41kb.
• Реферат электронная таблица Excel, 324.13kb.
• Урок биологии-9 класс. Тема «Многообразие живого мира. Основные свойства», 52.53kb.
• Личность педагога Основные свойства педагога, 54.36kb.
• Сорбционные свойства и проницаемость материалов. Основные характеристики, приборы, 54.52kb.
• Теплоизоляционные экологически безопасные материалы для ограждающих конструкций зданий, 104.31kb.

ТМ к лекции № 6


Основные свойства числовых характеристик


7.1 Теоремы о математических ожиданиях


Теорема 1. Математическое ожидание постоянной равно этой постоянной.

Доказательство. Мы можем рассматривать постоянную величину как предельный случай случайной величины, которая принимает единственное значение с вероятностью, равной 1. Тогда

Mc=1c=c

Теорема 2. Математическое ожидание от алгебраической суммы случайных величин равно алгебраической сумме математических ожиданий от слагаемых.



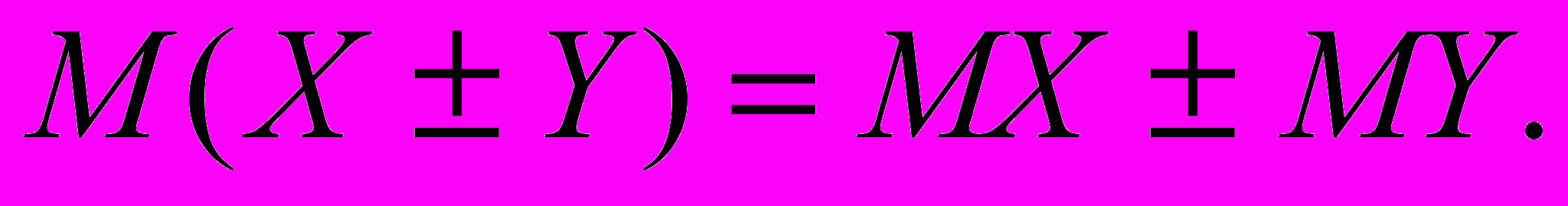
Доказательство. Случай 1. Пусть X и Y две дискретные случайные величины с конечным числом возможных значений. Тогда



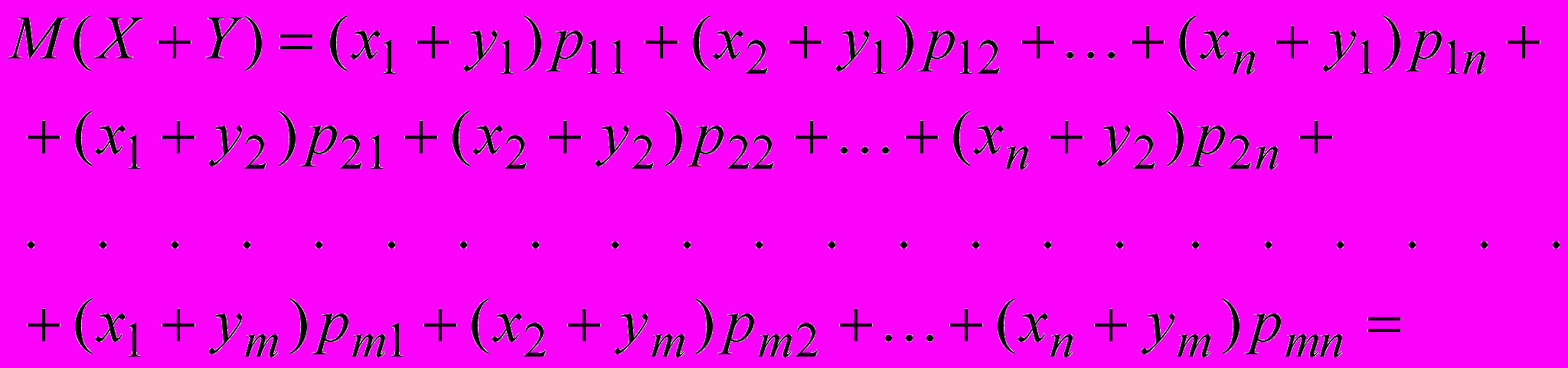
Раскроем скобки и произведем перегруппировку



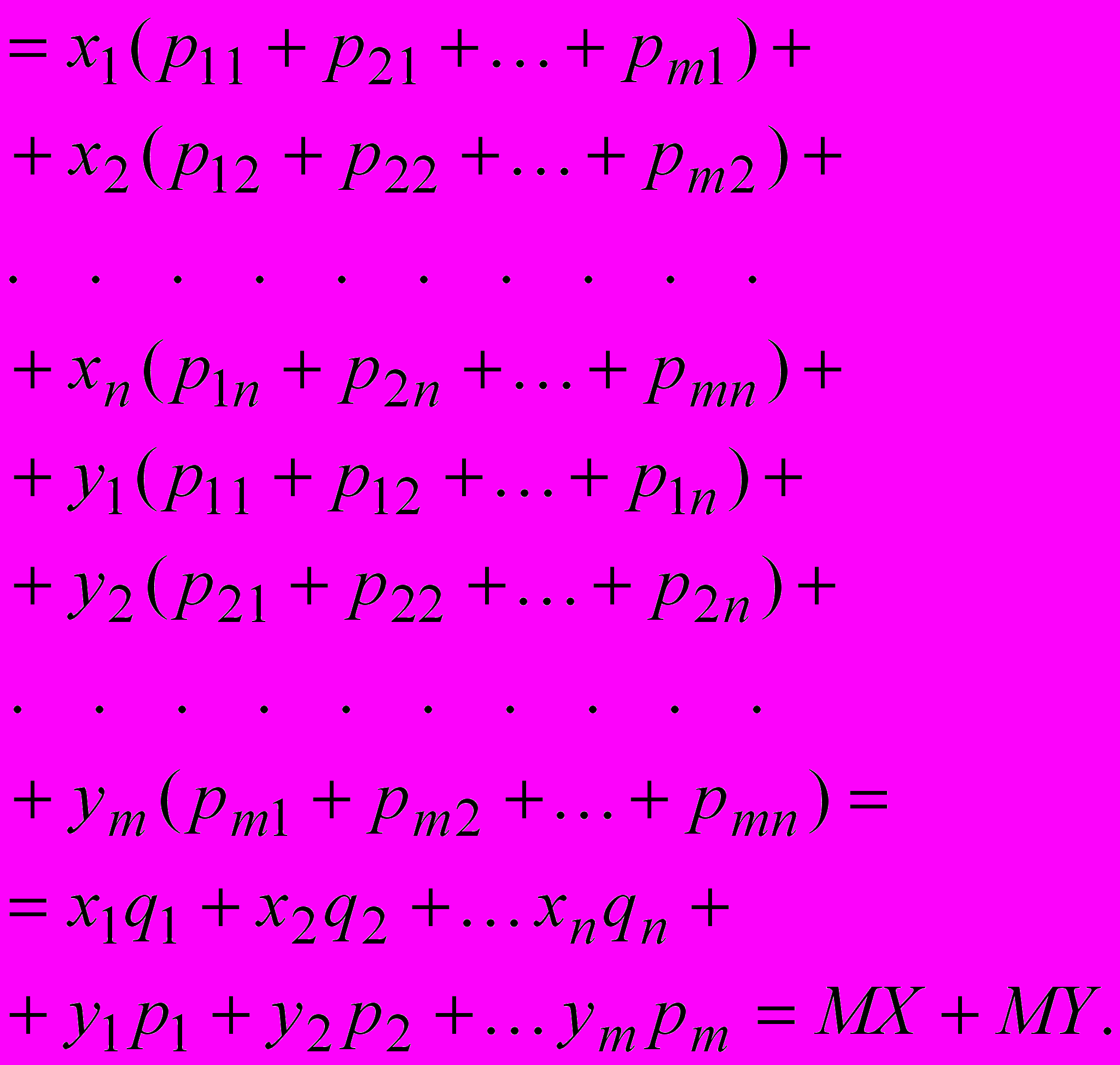
Проведем еще раз тоже доказательство в обозначениях сумм.



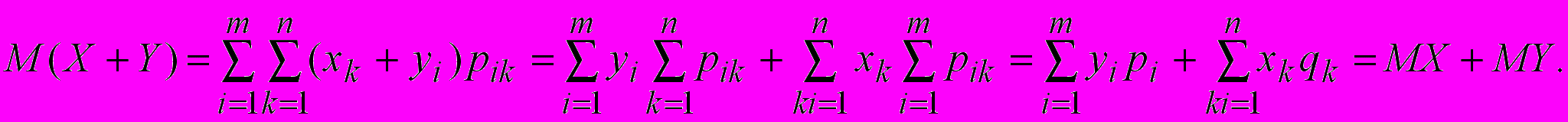
Случай 2. Пусть X и Y две непрерывные случайные величины с плотностью распределения p(x,y). Тогда



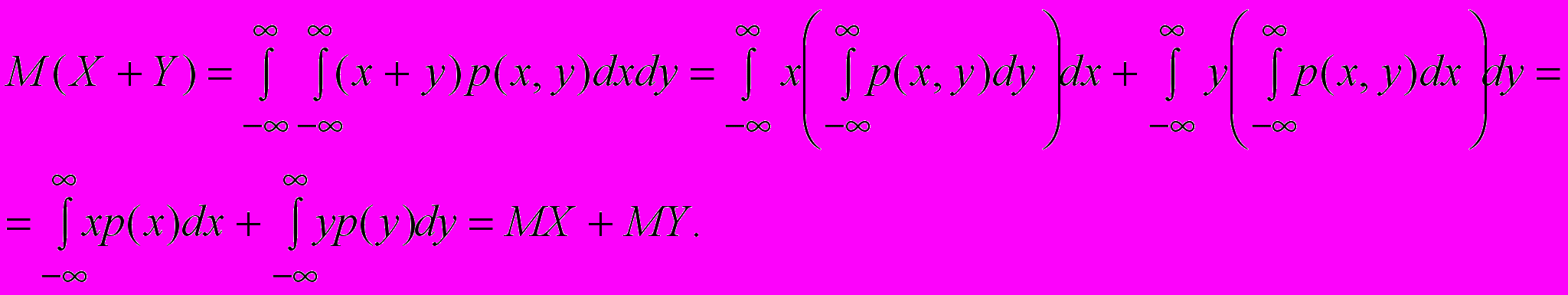
Теорема 3. Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий от сомножителей.



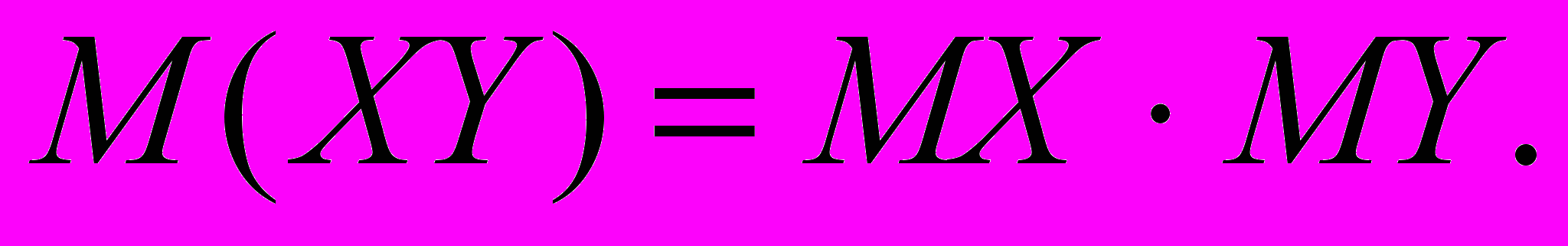
Случай 1. Пусть X и Y две дискретные случайные величины с конечным числом возможных значений. Так как X и Y независимы, то p_ik=p_ip_k. Тогда



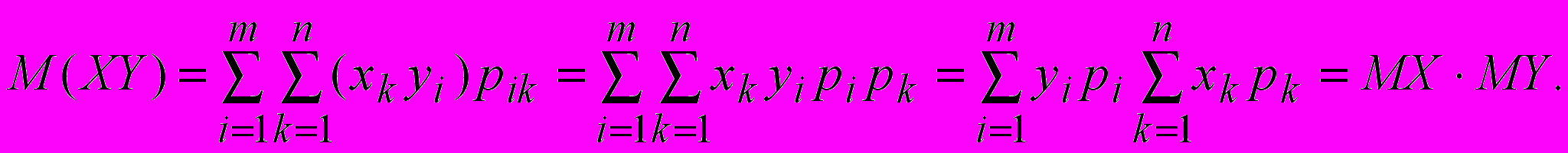
Случай непрерывных случайных величин рассмотреть самостоятельно.

Теорема 4. Постоянный сомножитель можно вынести за знак математического ожидания.



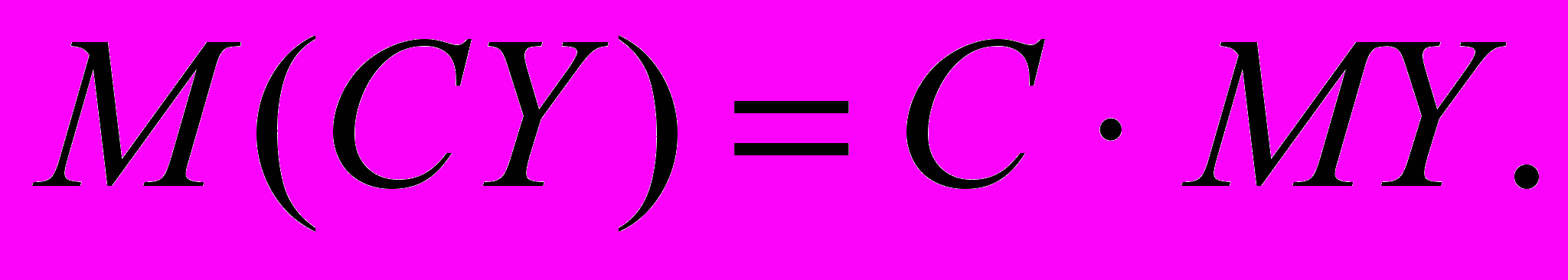
где C=const.

Доказательство. Считая, что постоянная величина есть предельный случай случайной величины, применим теорему 3. Очевидно, что C и Y независимы. Отсюда следует утверждение.

Следствие. Математическое ожидание отклонения равно 0.

Доказательство. M(X-MX)=MX- M(MX)= MX- MX=0.


7.2. Теоремы о дисперсиях


Теорема 1. Дисперсия постоянной равна нулю.

Доказательство. Мы можем рассматривать постоянную величину как предельный случай случайной величины, которая принимает единственное значение с вероятностью, равной 1. Тогда



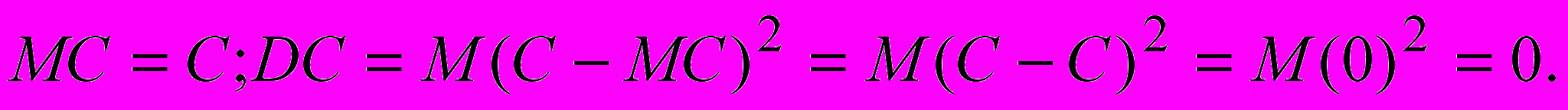
Теорема 2. Постоянный сомножитель можно вынести за знак дисперсии под знаком возведения в квадрат.



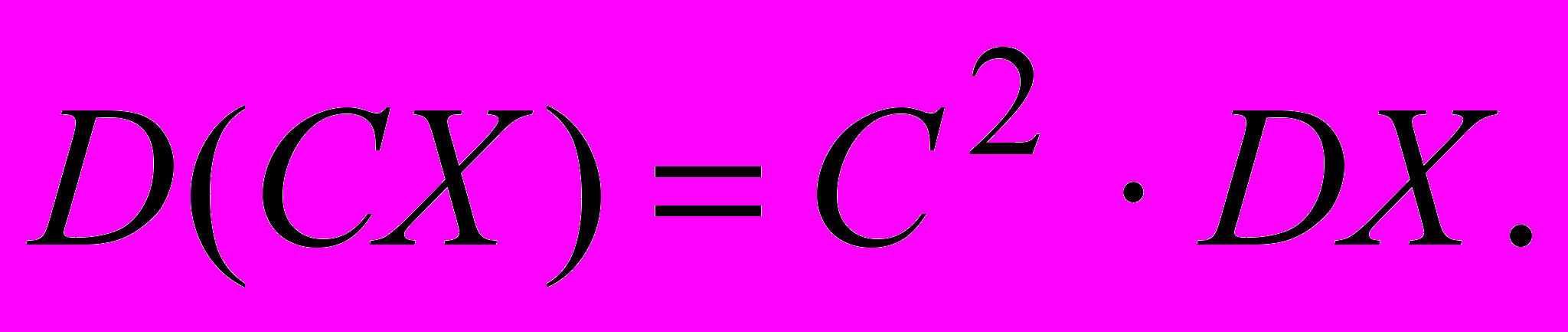
где C=const.

Доказательство.



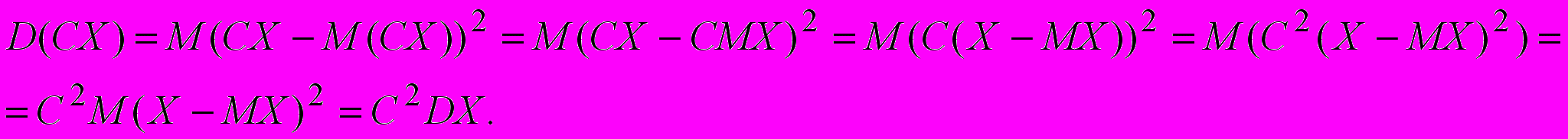
Теорема 3. Дисперсия суммы случайных независимых величин равно сумме дисперсий слагаемых.



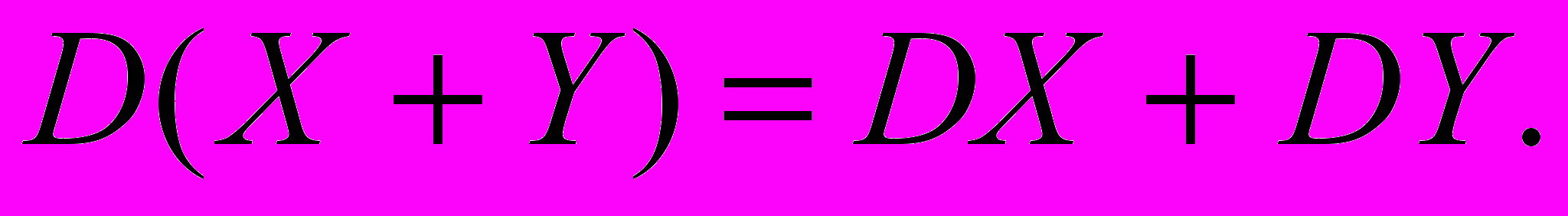
Доказательство. Из независимости случайных величин и следствия получаем



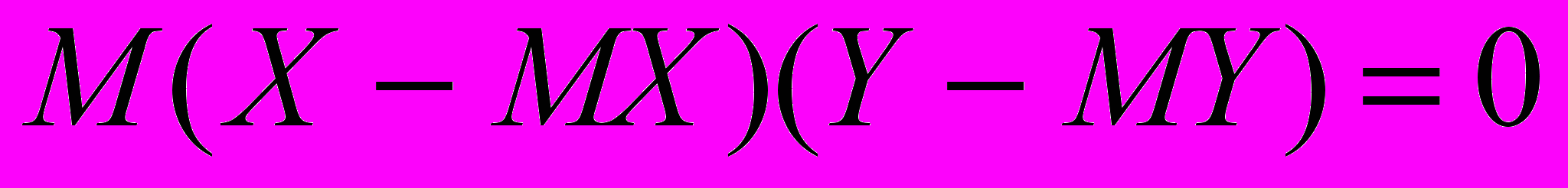
Тогда



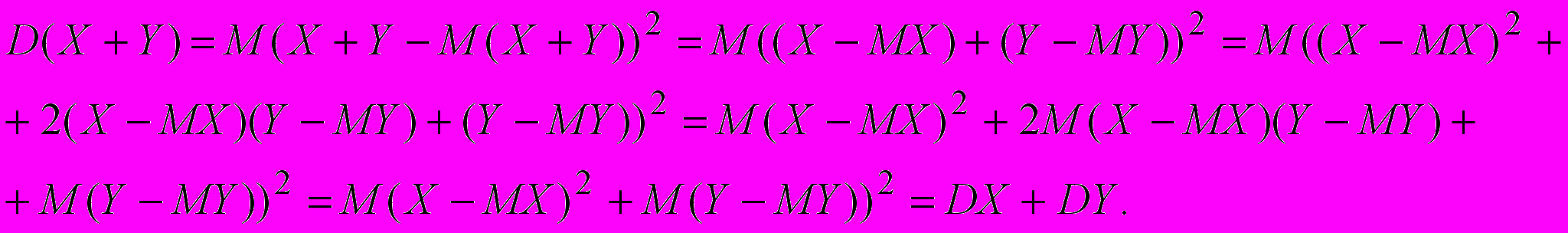
Следствие 1. Дисперсия случайной величины неотрицательна. Причем DX=0 только тогда, когда X=const.

Доказательство. Так как (X-MX)²0, то DX=M (X-MX)²0. Величина (X-MX)²=0 только тогда, когда X-MX=0. Или X=MX=const.

Следствие 2. Дисперсия разности двух случайных независимых величин равна сумме дисперсий слагаемых.



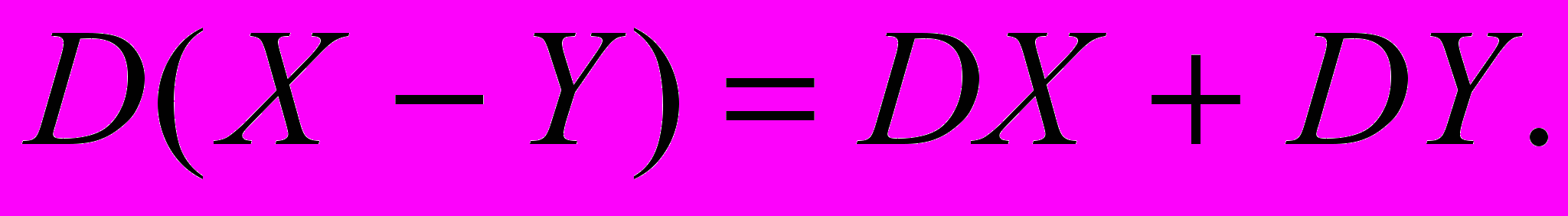
Доказательство



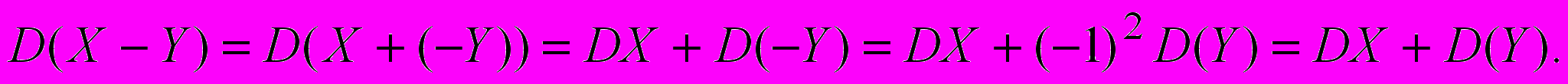
Следствие 3. Дисперсия равна



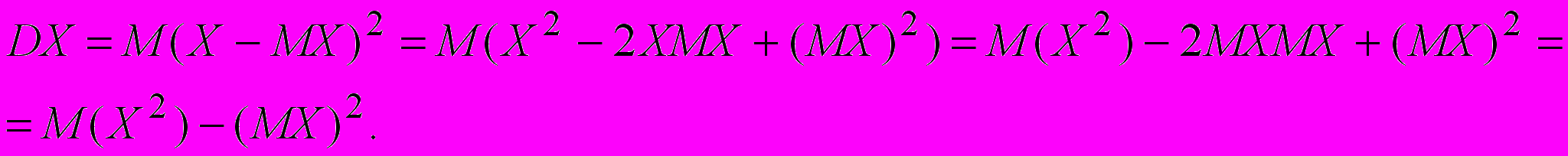
Сравнивать две случайные величины с разными характеристиками сложно. Поэтому для сравнения их нормируют по формуле U=(X-MX)/. Тогда



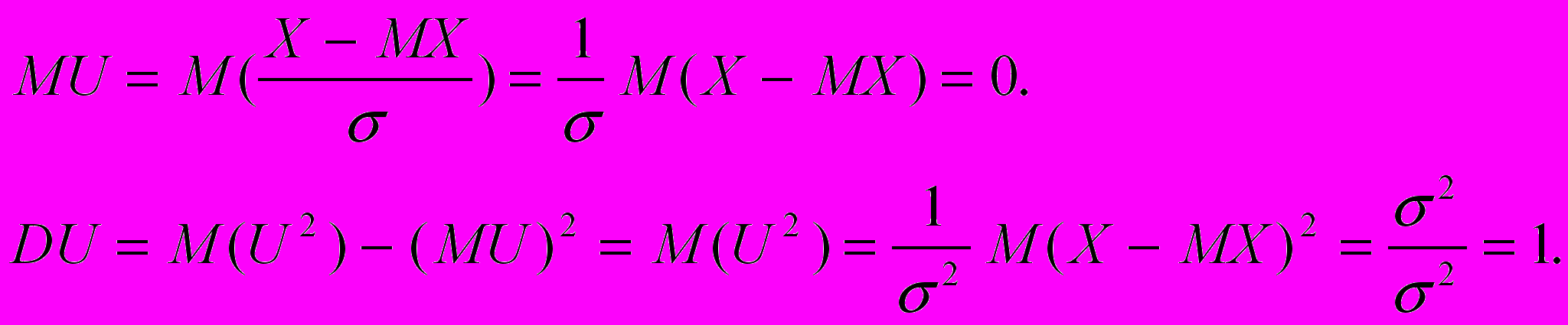
7.3. Ковариация


Определение. Ковариацией двух случайных величин X и Y называется величина (обозначается cov(X,Y)), равная



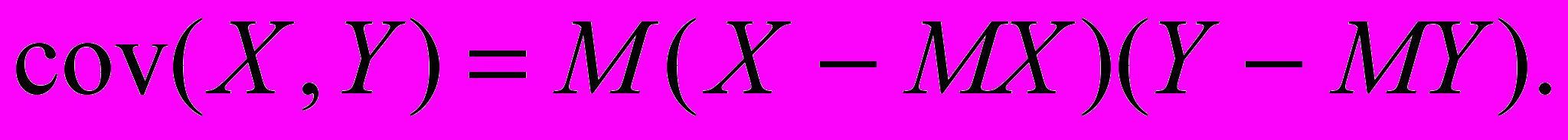
Из свойств математических ожиданий



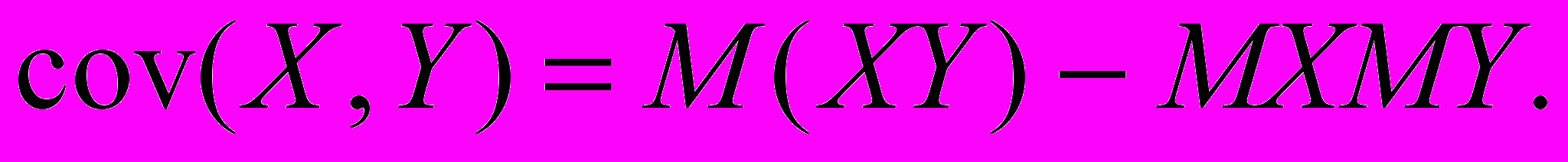
Если случайные величины X и Y независимы, то cov(X,Y)=0. Т. е. отличной от нуля может быть ковариация только для зависимых величин.

Свойства.

1. Постоянный сомножитель можно вынести за знак ковариации



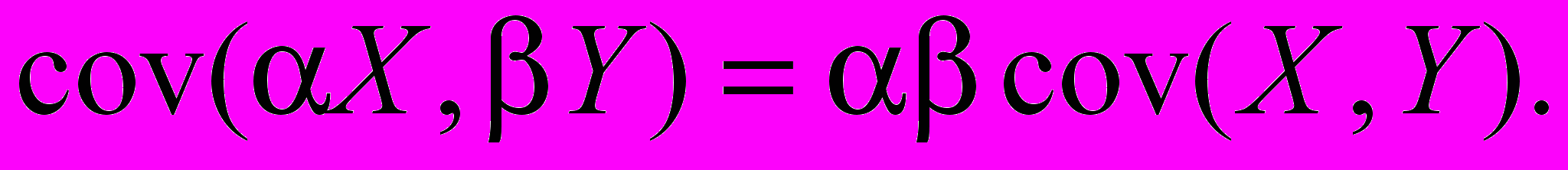
2. Ковариация от алгебраической суммы равна алгебраической сумме математических ожиданий от слагаемых, как по первому, так и по второму операнду.



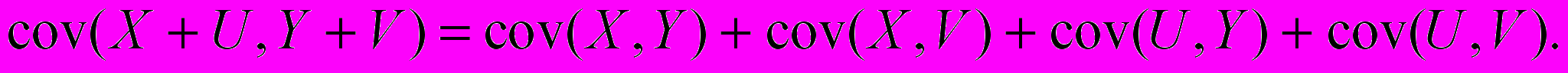
Доказательство следует из свойств математического ожидания. Доказать самостоятельно.

3. Дисперсия суммы равна



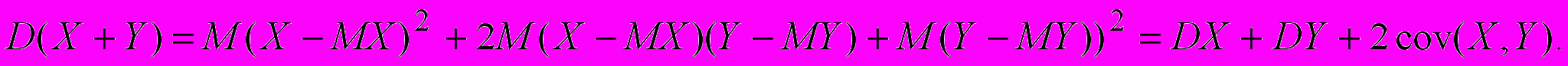
Доказательство следует из формулы для суммы дисперсий (см. лекцию 7). Доказать самостоятельно.

Ковариация не очень удобна для практических применений из-за свойства 1. Оно показывает, что при изменении масштаба измерения одного из операндов, ковариация меняется.


7.4. Коэффициент корреляции


Определение. Коэффициентом корреляции двух случайных величин X и Y называется величина (обозначается r_XY), равная



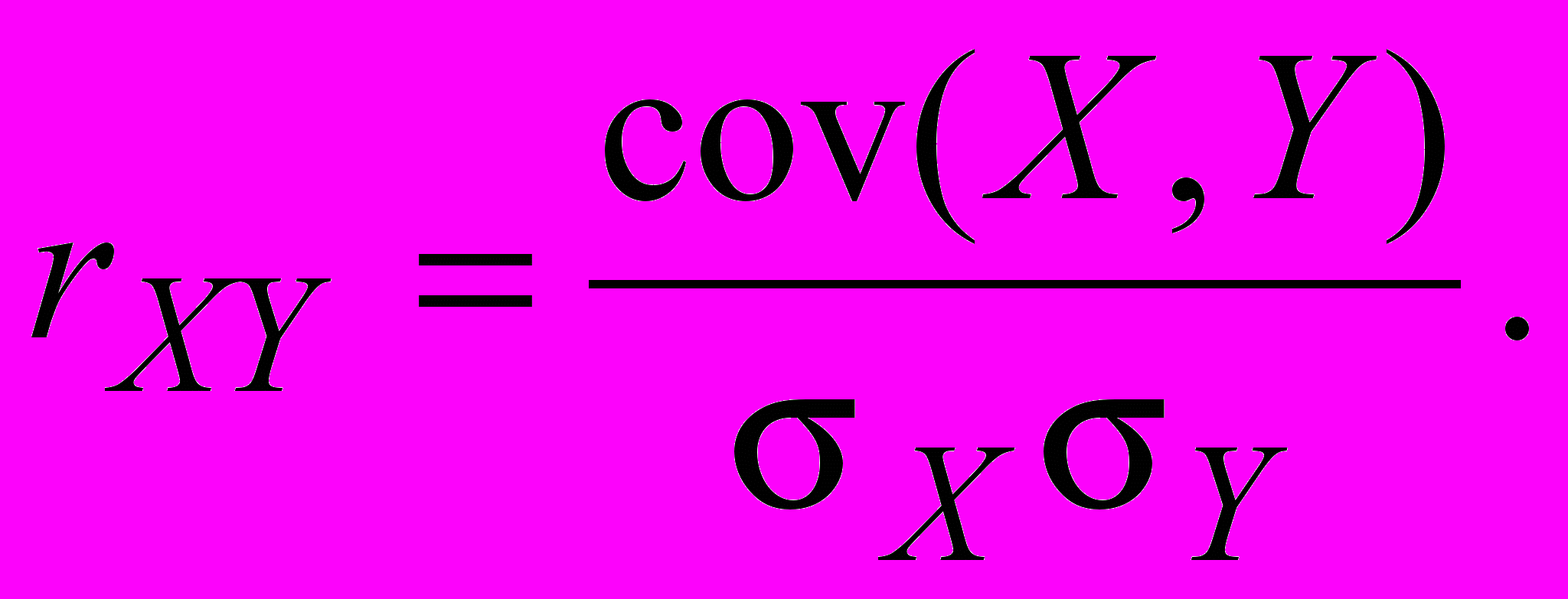
Коэффициент корреляции - это ковариация нормированных случайных величин U=(X-MX)/_X и V=(Y-MY)/_Y. Покажем это:



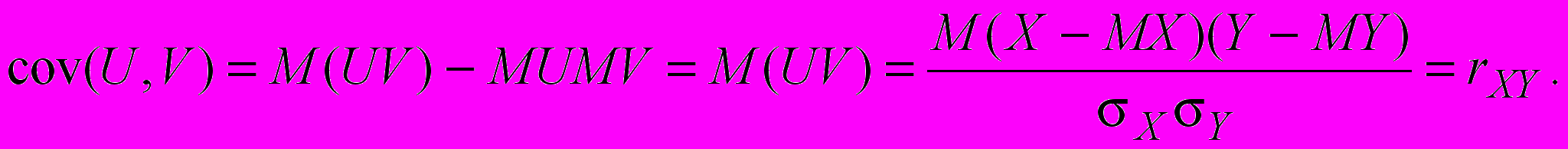
Свойства.

1. Коэффициент корреляции не меняется при линейной замене операндов. Т. е. если заменить X на X+ и Y на Y+, где ,,, - const, то коэффициент корреляции не изменится. Доказать самостоятельно.

2. Коэффициент корреляции удовлетворяет неравенству



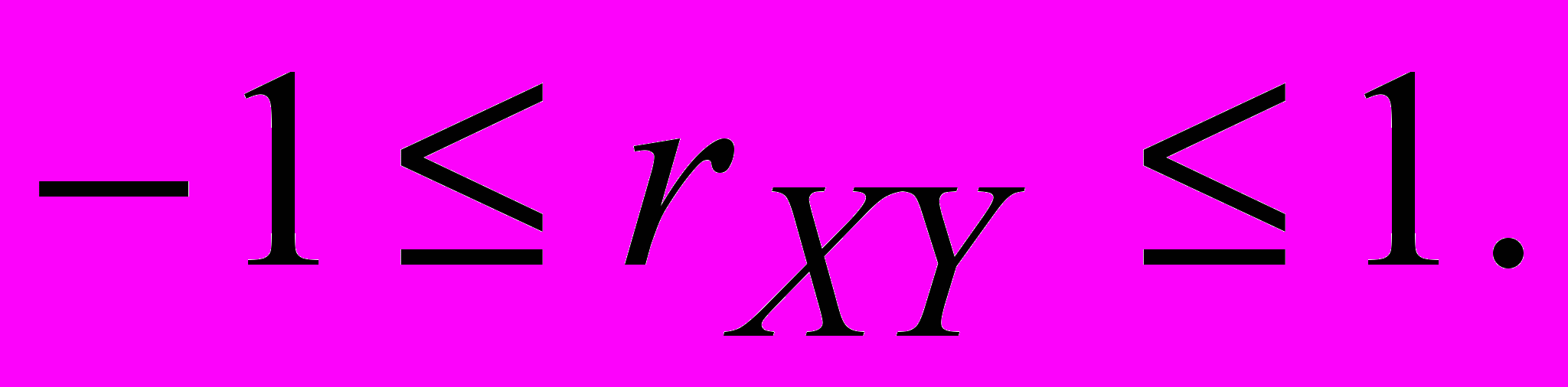
Доказательство, Найдем дисперсию суммы двух нормированных случайных величин U=(X-MX)/_X и V=(Y-MY)/_Y .



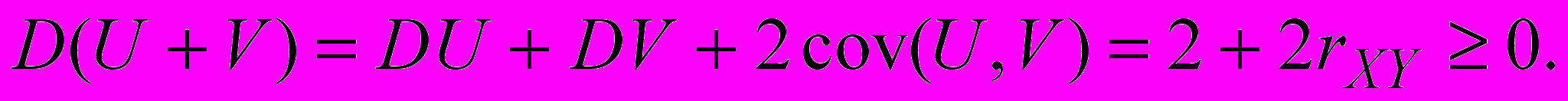
Откуда следует, что -1r_XY. Аналогично рассмотрим дисперсию их разности и покажем, что r_XY1. Доказать самостоятельно.

3. Если r_XY=1, то между случайными величинами X и Y существует линейная зависимость вида Y= X+, где , - const.

Схема доказательства, Пусть r_XY=-1. Тогда дисперсия суммы двух нормированных случайных величин U и V равна 0. По свойству дисперсий U+V= const. Откуда следует утверждение. Доказать самостоятельно.

4. Если случайные величины X и Y независимы, то r_XY =0. Доказать самостоятельно.

Обратное утверждение неверно. Это значит, что если r_XY =0, то утверждать, что случайные величины X и Y независимы нельзя.


Пример.

Пусть случайная величина X имеет ряд распределения

X	-1	0	1
P	0,25	0,5	0,25

Тогда MX=-10,25+00,5+10,25=0. Пусть Y=X². Тогда случайные величины X и Y зависимы. Вычислим ковариацию

Cov(X,Y)=M(XY)-MXM(X²)=M(X³)-0 M(X²)= M(X³)

Но в нашем случае M(X³)= M(X)=0. Значит r_XY =0, но случайные величины X и Y зависимы.

Коэффициент корреляции является мерой линейной зависимости. Равенство r_XY = 0 означает, что отсутствует линейная зависимость, но может быть, как в нашем примере, нелинейная зависимость. Чем ближе r_XY к единице, тем ближе связь к линейной.