Программы вступительных экзаменов в средние специальные учебные заведения РФ для поступающих на базе основного общего образования. Программа по русскому языку и литературе
| Вид материала | Программа |
- Программа по русскому языку и литературе для поступающих в Волгоградский государственный, 42.32kb.
- У языку для поступающих на базе основного общего образования соответствуют федеральному, 733.86kb.
- Рабочая программа по русскому языку (наименование учебного предмета), 611.93kb.
- Методика подготовки к егэ по русскому языку и литературе, 44.61kb.
- Программы вступительных испытаний для поступающих по программам бакалавриата (специалиста), 3816.01kb.
- Рабочая программа по русскому языку 9 класс, 690.41kb.
- Рабочие программы по русскому языку и литературе для общеобразовательных учреждений, 8271.99kb.
- Рабочая программа педагога Чуприной Людмилы Максимовны учителя русского языка и литературы, 1679.13kb.
- Вопросы для вступительных испытаний по литературе (собеседование) для поступающих, 24.14kb.
- Программа вступительных экзаменов по русской литературе русская литература, 50.54kb.
ПРОГРАММЫ ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ
В СРЕДНИЕ СПЕЦИАЛЬНЫЕ УЧЕБНЫЕ ЗАВЕДЕНИЯ РФ
ДЛЯ ПОСТУПАЮЩИХ НА БАЗЕ ОСНОВНОГО ОБЩЕГО ОБРАЗОВАНИЯ.
ПРОГРАММА ПО РУССКОМУ ЯЗЫКУ И ЛИТЕРАТУРЕ.
Общие указания.
На письменном экзамене по русскому языку (диктант) и устном экзамене по русскому языку и литературе экзаменующийся должен показать знания русского языка и литературы в объеме данной программы.
При подготовке к письменному экзамену особое внимание необходимо обратить на материал, связанный с орфографией и пунктуацией.
В билет для устного экзамена по русскому языку и по литературе включаются вопросы, как по русскому языку, так и по литературе, а также дается предложение для полного синтаксического разбора.
Кроме того, экзаменующемуся может быть предложено сделать фонетический, морфологический, словообразовательный разбор одного слова.
^ РУССКИЙ ЯЗЫК.
Фонетика и графика.
Звуки гласные ударные и безударные; ударение в слове. Звуки согласные твердые и мягкие; звуки согласные звонкие и глухие. Звуки и буквы. Алфавит. Обозначение мягкости согласных на письме. Звуковое значение букв е, ё, ю, я.
Лексика и фразеология.
Лексическое значение слова. Многозначные и однозначные слова. Прямое и переносное значение слов. Омонимы, Синонимы. Антонимы.
Общеупотребительные слова. Профессиональные слова. Диалектные слова. Заимствованные снова. Устаревшие слова. Неологизмы. Понятие о фразеологизме.
Словообразование.
Основа и окончание слова. Приставка, корень, суффикс. Чередование гласных и согласных в корнях слов. Способы словообразования в русском языке. Сложные и сложносокращенные слова.
Морфология.
Имя существительное. Общее значение, морфологические признаки и синтаксическая роль.
Три склонения существительных. Разносклоняемые существительные. Несклоняемые существительные. Род имен существительных. Изменение существительных по падежам и числам.
Имя прилагательное. Общее значение, морфологические признаки и синтаксическая роль.
Качественные, относительные и притяжательные прилагательные. Полные и краткие качественные прилагательные. Степени сравнения качественных прилагательных, образование степеней сравнения прилагательных. Род, число и падеж прилагательных. Способы образования прилагательных.
Имя числительное. Общее значение, морфологические признаки и синтаксическая роль.
Числительные количественные и порядковые. Числительные простые и составные. Числительные дробные и собирательные. Склонение порядковых и количественных числительных.
Местоимение. Общее значение, морфологические признаки и синтаксическая роль.
Склонение местоимений; правописание личных местоимений (3-го лоща) после предлогов. Образование неопределенных местоимений. Образование отрицательных местоимений.
Глагол. Общее значение, морфологические признаки и синтаксическая роль.
Переходные и непереходные глаголы. Виды глагола. 1 и 2 спряжения. Разноспрягаемые глаголы.
Формы изменения глагола: наклонение, число, род (в прошедшем времени и условном наклонении). Безличные глаголы.
Способы образования глаголов.
Причастие. Причастие кок особая форма глагола. Признаки глагола и прилагательного у причастия. Действительные страдательные причастия. Причастия настоящего и прошедшего времени. Полные и краткие страдательные причастия. Роль причастий в предложении. Склонение полных причастий. Изменение кратких причастий.
Деепричастие. Деепричастие как особая форма глагола. Признаки глагола и наречия у деепричастия. Деепричастия совершенного и несовершенного вида и их образование.
Наречие. Общее значение, морфологические признаки и синтаксическая роль. Степени сравнения наречий.
Предлог. Предлог как служебная часть речи.
Непроизводные и производные предлоги.
Союз. Союз как служебная часть речи. Союзы простые и составные. Союзы сочинительные и подчинительные.
Частицы. Частица как служебная часть речи. Формообразующие, отрицательные и модальные частицы.
Междометия. Значение междометий и их роль в речи.
Орфограммы.
Понятие об орфограмме.
Орфограммы – буквы. Употребление буквы ь для обозначения мягкости согласных. Разделительные ъ и ь.
Буквы з и с на конце приставок на –з(с). Гласные е–и в приставках пре– и при–. Правописание проверяемых гласных и согласных в корне слова. Правописание, непроверяемых гласных и согласных в корне слова Правописание непроизносимых согласных в корне слова.
Чередующиеся о–а в корнях гор – гар , кос – кос, лож – лаг, рос – раст. Чередующиеся гласные е–и в корнях мер – мир, дер – дир и других. Соединительные гласные о–е в сложных словах.
Правописание гласных в падежных окончаниях существительных.
Буквы о и е после шипящих в окончаниях прилагательных. Н и нн в суффиксах прилагательных –ан–(–ян–), –ин–, –онн– (–енн–).
Различие на письме суффиксов –к– и –ск–.
Правописание гласных в окончаниях количественных числительных. Употребление ь в середине и на конце числительных.
Правописание гласных в личных окончаниях глаголов.
Буква ь на конце глаголов после шипящих. Различение на письме –тся– и –ться–. Гласные в суффиксах глагола –ова– (–ева–), –ыва– (–ива–). Мягкий знак в глаголах повелительного наклонения.
Правописание гласных в падежных окончаниях причастий.
Правописание гласных в суффиксах действительных и страдательных причастий. Н и нн в суффиксах полных и кратких причастий.
Различие о и а на конце наречий. Мягкий знак на конце наречий, оканчивающихся на шипящие.
Орфограммы – дефисы. Слитное и дефисное написание слов с пол–. Дефис в сложных прилагательных. Дефис в местоимениях с суффиксами –то, –либо, –нибудь и приставкой кое–. Дефисное написание наречий. Дефис в предлогах из–за, из–под. Дефис в междометиях.
Орфограммы – слитное и раздельное написание.
Раздельное написание предлогов с местоимениями. Слитное и раздельное, написание наречий.
Слитное и раздельное написание предлогов (в течение, ввиду и т.д.).
Слитное и раздельное написание союзов. Отличие союзов зато, тоже, чтобы от местоимений с предлогом и частицами; отличие союза также от наречия с частицей.
Не с именами существительными. Не с именами прилагательными. Не и ни в местоимениях. Не с глаголами. Не с причастиями. Не с деепричастиями. Не и ни в наречиях. Не с наречиями на –о (–е). Слитное и раздельное написание частиц не и ни с разными частями речи.
Синтаксис.
Словосочетание и предложение. Отличие словосочетания от слова и предложения. Главное и зависимое слово в словосочетании.
Виды связей слов в словосочетании. Связь между подлежащим и сказуемым.
Виды предложений по цели высказывания; восклицательные предложения.
Простые предложения с двумя главными членами. Подлежащее и способы его выражения. Сказуемое и способы его выражения.
Второстепенные члены предложения: дополнение, определение, обстоятельства места, времени, причины и другие; способы их выражения.
Простые предложения с одним главным членом в форме сказуемого; Простое предложение с одним главным членом в форме подлежащего.
Неполные предложения.
Предложения с однородными членами. Однородные члены предложения, связанные союзами и интонацией. Обобщающие слова в предложениях с однородными членами.
Предложения с обращениями, вводными словами и междометиями. Обращение, его место в предложении. Предложения с вводными словами. Вводные предложения.
Предложения с обособленными членами. Обособленные определения: причастный оборот, приложение. Уточняющие члены предложения. Сравнительный оборот.
Обособленные обстоятельства. Деепричастные обороты.
Обособленные обстоятельства с предлогами на, невзирая на, благодаря и т. д.
Прямая и косвенная речь. Прямая речь. Косвенная речь.
Цитата.
Сложное предложение. Сложные предложения с союзами и без союзов.
Сложносочиненные предложения. Отличие сложносочиненного предложения от простого предложения с однородными членами, связанными сочинительными союзами.
Сложноподчиненные предложения. Главное и придаточное предложения. Виды придаточных предложений. Союзы и союзные слова как средство связи придаточного предложения по отношению к главному.
Сложноподчиненные предложения с несколькими придаточными (с соподчинением, однородным, неоднородным и последовательным подчинением).
Бессоюзные сложные предложения. Смысловые взаимоотношения между частями бессоюзного сложного предложения.
Сложные предложения с различными видами связи (союзной и бессоюзной). Различные виды сложных предложений с союзной и бессоюзной связью.
Пунктуация.
Понятие о пунктограмме.
Тире между подлежащим и сказуемым.
Запятая между однородными членами в предложении. Двоеточие и тире при обобщающих словах в предложениях с однородными членами.
Знаки препинания при обращении. Знаки препинания при вводных словах и предложениях.
Знаки препинания в предложениях с междометиями.
Знаки препинания при обособленных второстепенных и уточняющих членах предложения. Выделение запятой сравнительного оборота.
Знаки препинания в предложениях с прямой речью.
Знаки препинания при цитировании.
Запятая между частями сложносочиненного предложения. Запятая между главным в придаточным предложениями.
Общие сведения о языке.
Роль языка в жизни общества.
Русский язык - один из основных международных языков.
Стилистика.
Понятие о стиле.
Стили русского литературного языка и их особенности.
^ ЛИТЕРАТУРНЫЕ ПРОИЗВЕДЕНИЯ.
Д.И.Фонвизин «Недоросль».
А.С.Грибоедов «Горе от ума».
А.С.Пушкин «Капитанская дочка», «Евгений Онегин»; стихотворения: «К Чаадаеву», «Вольность», «Я памятник себе воздвиг...».
М.Ю.Лермонтов «Мцыри», «Песня про купца Калашникова», «Герой нашего времени»; стихотворения: «Смерть поэта», «Бородино», «Родина».
Н.В.Гоголь «Ревизор», «Шинель», «Мёртвые души».
А.И.Герцен «Былое и думы» (избранные главы).
И.С.Тургенев «Бирюк», «Ася».
Н.А.Некрасов «Русские женщины», «Мороз, Красный нос».
Л.Н.Толстой «После бала», «Детство» (отдельные главы).
В.Г.Короленко «Парадокс», «Огоньки».
A.П.Чехов «Хамелеон».
М.Горький «Детство» (главы), «Песня о соколе», «Старуха Изергиль».
В.В.Маяковский «Необычайное приключение, бывшее с Вл. Маяковским на даче», «Хорошее отношение к лошадям».
Л.Андреев, А.П.Платонов (1 рассказ на выбор).
Произведение о Великой Отечественной войне (А. Ахматовой, А.Т. Твардовского, Ф.А. Абрамова и др. 2 - 3 на выбор).
Произведение об отношении к природе, миру (Е.И. Носова, Ф.И. Абрамова, Ю.В. Бондарева).
Стихотворения о Родине (1 - 2 на выбор).
^ ОБРАЗЕЦ ДИКТАНТА.
Однажды вечером, кончив дневной сбор винограда, партия молдаван, с которой я работал, ушла на берег моря, а я и старуха Изергиль остались под густой тенью виноградных лоз и, лежа на земле, молчали, глядя, как тают в голубой мгле ночи силуэты тех людей, что пришли к морю.
Они шли, пели и смеялись; мужчины – бронзовые, с пышными, черными усами и густыми кудрями до плеч, в коротких куртках и широких шароварах; женщины и девушки – веселые, гибкие, с темно-синими глазами, тоже бронзовые. Их волосы, шелковые и черные, были распущены, ветер, теплый и легкий, играя ими, звякал монетами, вплетенными в них. Ветер тек широкой, ровной волной, но иногда он точно прыгая через что-то невидимое и, рождая сильный порыв, развевал волосы женщин в фантастические гривы, вздымавшиеся вокруг их голов. Это делало женщин, странными и сказочными. Они уходили все дальше от нас, а ночь и фантазия одевали их все прекраснее…
Воздух был пропитан острым запахом моря и жирными испарениями земли, незадолго до вечера обильно смоченной дождем. Еще и теперь по небу бродили обрывки туч, пышные, странных очертаний и красок. Между ними ласково блестели тёмно-голубые клочки неба, украшенные золотыми крапинками звезд. Все это – звуки и запахи, тучи и люди – было странно красиво и грустно, казалось началом чудесной сказки.
198 слов.
М. Горький.
^ ПРОГРАММА ПО МАТЕМАТИКЕ.
Общие положения.
Приведенные ниже требования к математической подготовке поступающих в средние специальные учебные заведения согласованы с Временным государственным образовательным стандартом по образовательной области «Математика» для основной школы.
Содержимое программы сгруппировано вокруг стержневых линий школьного курса математики: «Числа и вычисления», «Выражения и их преобразования», «Уравнения и неравенства», «Функция», «Геометрические фигуры. Измерение геометрических величин».
На экзамене по математике поступающие в средние специальные учебные заведения должны показать:
1) четкое знание определений математических понятий, формулировок теорем, основных формул;
2) умение доказывать теоремы и выводить формулы, проводить доказательные рассуждения в ходе решения задач в устном и письменном изложении;
3) уверенное владение основными умениями и навыками, предусмотренными программой, умение решать типовые задачи.
Программа по математике для поступающих в средние специальные учебные заведения состоит из трех разделов. В первом разделе перечислены основные понятия и факты, которые должны знать поступающие и уметь применять. Второй раздел содержит теоремы и формулы, которые надо уметь формулировать и доказывать. Из вопросов этого раздела формируется содержание теоретической части экзаменационных материалов. В третьем разделе указаны основные умения и навыки, которыми должны владеть поступающие.
Раздел 1. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ФАКТЫ.
Числа и вычисления.
- Натуральные числа. Делители и кратные натурального числа. Четные и нечетные числа. Признаки делимости на 2, 3, 5, 10 и 9. Простые составные числа. Понятие о разложении натурального числа на простые множители. Наибольший общий делитель. Наименьшее общее кратное.
- Положительные и отрицательные числа. Противоположные числа. Модуль числа, его геометрический смысл. Сравнение положительных и отрицательных чисел.
- Дроби. Правильные и неправильные дроби. Целая и дробная части числа. Основное свойство дроби. Среднее арифметическое нескольких чисел.
4. Десятичная дробь. Приближенное значение числа. Округление чисел. Проценты. Основные задачи на проценты.
5. Понятие о числе как результате измерения. Рациональные числа. Представление рациональных чисел в виде периодических бесконечных десятичных дробей.
6. Изображение чисел на прямой. Координата точки. Прямоугольная система координат на плоскости, абсцисса и ордината точки;
- Пропорция. Основное свойство пропорции. Понятие о прямой и обратной пропорциональности величин.
- Понятие об иррациональных числах. Действительные числа. Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств.
- Понятие об изменении величин, абсолютной и относительной погрешности приближенного значения. Запись чисел в стандартном виде.
- Квадратный корень.
Выражения и их преобразования.
1. Числовые выражения. Применение букв для записи выражений. Числовое значение буквенного выражения. Вычисления по формулам. Простейшие преобразования выражений: раскрытие скобок, приведение подобных слагаемых.
2. Многочлен. Степень многочлена. Сложение, вычитание, умножение многочленов. Разложение многочлена на множители. Формулы сокращенного умножения.
- Квадратный трехчлен. Разложение квадратного трехчлена на множители.
- Алгебраическая дробь. Основное свойство дроби. Сокращение алгебраических дробей. Сложение, вычитание, умножение и деление алгебраических дробей.
- Степень с натуральным показателем и ее свойства. Степень с целым показателем. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни.
- Корень n-й степени и его свойства. Степень с рациональным показателем и ее свойства.
7. Арифметическая прогрессия. Формулы n-го члена и суммы n первых членов арифметической прогрессии.
8. Геометрическая прогрессия. Формулы n-го члена и суммы n первых ее членов. Сумма бесконечно убывающей геометрической прогрессии.
Уравнения и неравенства.
1. Уравнение. Корни уравнения. Линейные уравнения с одним неизвестным. Квадратное уравнение; формулы корней. Рациональное уравнение и его решение.
- Система уравнений. Решение системы двух линейных уравнений с двумя неизвестными и его геометрическая интерпретация. Решение простейших систем, содержащих уравнение второй степени.
- Линейное неравенство с одним неизвестным. Система линейных неравенств с одним неизвестным. Решение рациональных неравенств методом интервалов. Решение неравенств
второй степени с одним неизвестным.
Функция.
1. Функция. Способы задания функции. Область определения функции, область значений График функции. Свойства функции: монотонность функции, нули функции, интервалы знакопостоянства.
2. Функции: а) у = kx; б) у = kx + b; в) у = ах2; г) у = ах2 + bx + c; д) у = хn (n - натуральное число); е) у =
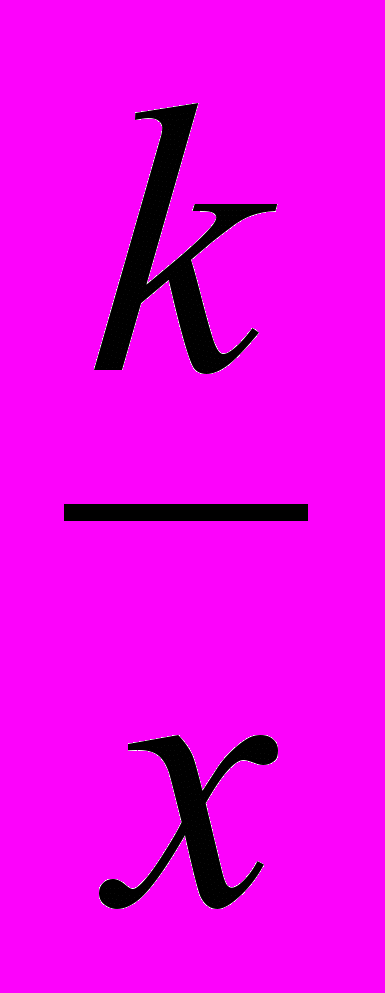 ; ж) у =
; ж) у = 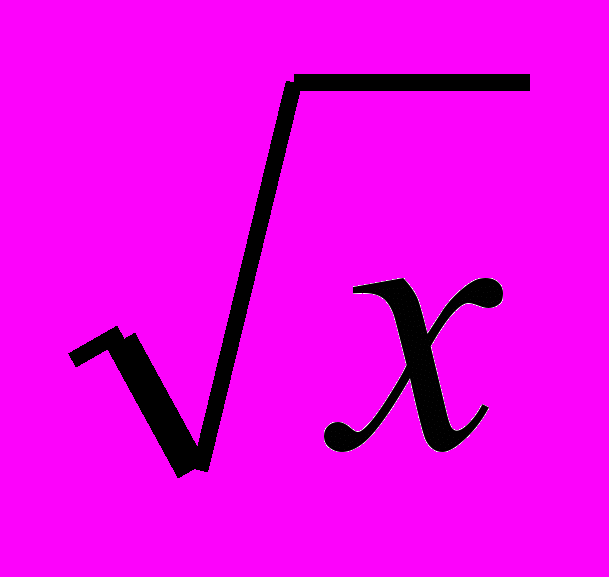 . Их свойства и графики.
. Их свойства и графики.Геометрические фигуры. Измерения геометрических величин.
- Смежные и вертикальные углы и их свойства. Пересекающиеся и параллельные прямые. Признаки параллельности прямых. Перпендикулярные прямые. Теоремы о параллельности и перпендикулярности прямых.
- Треугольник и его элементы. Виды треугольников. Свойства равнобедренного треугольника. Сумма углов треугольника. Внешний угол треугольника. Теорема о внешнем угле треугольника.
- Прямоугольный треугольник. Теорема Пифагора. Синус, косинус, тангенс угла. Соотношения между сторонами и углами прямоугольного треугольника.
- Параллелограмм и его свойства. Признаки параллелограмма. Прямоугольник, ромб, квадрат, их свойства. Трапеция. Правильные многоугольники.
- Окружность и круг. Касательная к окружности и ее свойства.
- Свойство серединного перпендикуляра к отрезку; окружность, описанная около треугольника. Свойство биссектрисы угла треугольника; окружность, вписанная в треугольник.
- Понятие о равенстве фигур. Признаки равенства треугольников.
- Понятие о подобии фигур. Признаки подобия треугольников.
- Примеры преобразования фигур, виды симметрии.
- Основные задачи на построение с помощью циркуля и линейки.
- Длина отрезка. Расстояние от точки до прямой.
- Градусное измерение угла. Измерение вписанных и центральных углов.
- Длина окружности. Длина дуги. Число .
- Понятие о площади, основные свойства площади. Площади прямоугольника, треугольника, параллелограмма, ромба, трапеции. Отношение площадей подобных фигур. Площадь круга и его частей.
- Выпуклые многоугольники. Сумма внутренних (внешних) углов выпуклого многоугольника. Правильные многоугольники. Площадь правильного многоугольника.
Раздел 2. ОСНОВНЫЕ ПРИЗНАКИ, СВОЙСТВА, ТЕОРЕМЫ И ФОРМУЛЫ.
Алгебра.
- Признаки делимости на 2, 3, 5, 9, 10.
- Степень с натуральным показателем и ее свойства.
- Степень с рациональным показателем и ее свойства.
- Корень n-й степени и его свойства.
- Арифметическая прогрессия и формула n-го ее члена.
- Геометрическая прогрессия и формула n-го ее члена.
- Функция у = kx, ее свойства и график.
- Функция у =
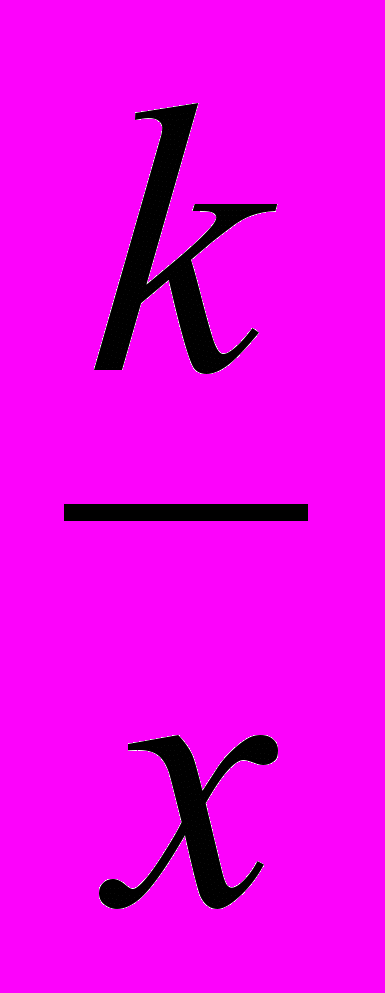 , ее свойства и график.
, ее свойства и график.
- Функция у = kx + b, ее свойства и график.
- Степенная функция, ее свойства и график,
11. Квадратичная функция, ее свойства и график,
- Квадратное уравнение и его решение. Формулы корней квадратного уравнения.
- Квадратный трехчлен, разложение его на множители.
- Формулы сокращенного умножения.
- Линейное уравнение и его решение. Решение уравнений, сводящихся к линейным (на конкретных примерах).
- Линейные неравенства и их решение. Решение систем линейных неравенств (на конкретных примерах).
17. Система двух линейных уравнений с двумя переменными и ее решение.
Геометрия.
- Свойства равнобедренного треугольника.
- Свойства биссектрисы угла треугольника.
- Признаки параллельности прямых.
- Теорема о сумме углов треугольника.
- Признаки подобия треугольников.
- Свойства параллелограмма и его диагоналей.
7. Свойства прямоугольника, ромба и квадрата.
8. Окружность, описанная около треугольника.
9. Окружность, вписанная в треугольник.
- Теорема о вписанном угле в окружность.
- Свойства касательной к окружности.
- Теорема Пифагора.
- Значение синуса, косинуса и тангенса для углов 300, 450, 600.
- Формулы площадей параллелограмма, треугольника и трапеции.
Раздел 3. ОСНОВНЫЕ УМЕНИЯ И НАВЫКИ.
Поступающие должны:
- Правильно употреблять термины, связанные с видами и способами их записи (натуральное, целое, рациональное, иррациональное число, обыкновенная дробь, десятичная дробь); читать и записывать числа; переходить от одной формы записи числа к другой (например, представлять десятичную дробь в виде обыкновенной; обыкновенную - в виде десятичной; проценты - в виде десятичной дроби).
- Сравнивать два числа (натуральное, обыкновенные дроби; положительные и отрицательные числа).
- Изображать числа точками координатной прямой, понимать связь отношений «больше», «меньше» с расположением точек на прямой.
- Бегло и уверенно выполнять арифметические действия с рациональными числами в ходе вычислений.
- Решать основные задачи на дроби и проценты.
6. Находить значение выражений, содержащих степени с натуральными и целыми показателями, квадратные и кубические корни.
7. При вычислениях сочетать устные и письменные приемы вычислений, применение калькулятора, использовать приемы, рационализирующие вычисления.
8. Составлять и решать пропорции, округлять целые числа и десятичные дроби.
9. Правильно употреблять буквенную символику, понимать смысл терминов «выражение», «тождественное преобразование», формулировку заданий: «упростить выражение», «разложить на множители».
10. Владеть техникой тождественных преобразований рациональных (целых и дробных) выражений; выполнять основные действия над степенями, многочленами, алгебраическими дробями и применять их при преобразовании выражений.
11. Владеть приемами разложения многочленов на множители (вынесение общего множителя за скобки, группировка, по формулам сокращенного умножения) и применять их в комбинации.
12. Уметь пользоваться специальными приемами преобразования выражений (выделение квадрата двучлена из квадратного трехчлена, разложение трехчлена на множители, применение формул сокращенного умножения и др.).
13. Выполнять преобразование числовых и буквенных выражений, содержащих квадратные корни (применение свойств арифметических квадратных корней, приведение подобных радикалов, исключение иррациональности в знаменателе или числителе дроби).
14. Составлять алгебраические выражения и уравнения при решении текстовых задач; осуществлять в формулах числовые подстановки и выполнять соответствующие расчеты.
15. Уметь решать линейные, квадратные уравнения, простейшие рациональные уравнения, сводящиеся к линейным или квадратным; системы линейных уравнений с двумя переменными и системы, в которых одно уравнение второй степени.
16. Решать линейные неравенства с одной переменной и их системы; понимать графическую, интерпретацию решения уравнений и систем уравнений, неравенств.
- Решать текстовые задачи с помощью составления уравнений.
- Владеть системой функциональных понятий (функция, значение функции, график, аргумент, область определения, область значений, возрастание, убывание, монотонность, сохранение знака), пользоваться ими в ходе исследования функций.
19. Читать и строить графики функций (линейная, прямая пропорциональность, обратная пропорциональность, квадратичная функция).
20. Находить значение функций, заданных формулой, таблицей, графиком, решать обратную задачу.
21. Уметь распознавать на чертежах и моделях геометрические фигуры (отрезки, углы, треугольники и их частные виды, четырехугольники и их частные виды, окружность, круг); изображать указанные геометрические фигуры; выполнять чертежи по условию задачи.
- Вычислять, значения геометрических величин (длин, углов, площадей), применяя изученные свойства фигур и формулы.
- Решать задачи на вычисление геометрических величин; проводить аргументацию в ходе решения задачи.
^ ПРОГРАММЫ ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ
В СРЕДНИЕ СПЕЦИАЛЬНЫЕ ЗАВЕДЕНИЯ РФ
ДЛЯ ПОСТУПАЮЩИХ НА БАЗЕ
СРЕДНЕГО (ПОЛНОГО) ОБЩЕГО ОБРАЗОВАНИЯ.
^ ПРОГРАММА ПО РУССКОМУ ЯЗЫКУ И ЛИТЕРАТУРЕ.
Общие указания.
Экзамен по русскому языку и литературе проводится в форме сочинения на одну из четырех-пяти по выбору экзаменующегося тем литературного и общественно-политического характера. При подготовке к сочинению особое внимание необходимо обратить на материал, связанный с орфографией и пунктуацией. На экзамене по русскому языку и литературе поступающий в среднее специальное учебное заведение должен показать:
- Знание указываемых ниже произведений русской литературы, понимание их идейного содержания и художественных особенностей.
- Понимание художественного, исторического и общественного значения литературного произведения в связи с общественно-политической обстановкой эпохи.
3. Умение обосновывать свое отношение к произведению.
- Понимание идейного богатства, высоких художественных достоинств русской литературы и ее мирового значения.
- Понимание общих закономерностей историко-литературного процесса.
6. Умение логически правильно, стилистически грамотно излагать свои мысли.
7. Орфографическую, грамматическую и пунктуационную грамотность.
Литературные произведения (на базе полной общеобразовательной школы).
А.С. Грибоедов. «Горе от ума».
А.С. Пушкин. «Евгений Онегин»; стихотворения (по выбору экзаменующегося).
М.Ю. Лермонтов. «Герой нашего времени»; стихотворения (по выбору экзаменующегося).
Н.В. Гоголь. «Мёртвые души».
А.Н.Островский. «Гроза».
И.А. Гончаров. «Обломов».
И.С.Тургенев. «Отцы и дети».
Н.Г. Чернышевский. «Что делать?»
М.Е. Салтыков-Щедрин. «История одного города», «Сказки» (по выбору экзаменующегося).
Н.А. Некрасов. «Кому на Руси жить хорошо»; стихотворения: «Коробейники», «Тройка», «В дороге», «Родина», «Внимая ужасам войны…» и др.
Ф.М. Достоевский. «Преступление и наказание» или «Идиот».
Л.Н. Толстой. «Война и мир».
А.П. Чехов. «Ионыч» и др. рассказы, «Вишневый сад» или «Дядя Ваня».
И.А. Бунин. «Солнечный удар», «Чистый понедельник» и др.
А.И. Куприн. «Гранатовый браслет» или «Олеся», «Поединок».
1 – 2 поэта «серебряного века» русской поэзии (по выбору).
А.М. Горький. «На дне».
А.И. Блок. Стихотворения (по выбору экзаменующегося). Поэма «Двенадцать».
С.А. Есенин. Стихотворения (по выбору экзаменующегося), поэма «Анна Снегина».
В.В. Маяковский. Стихотворения (по выбору экзаменующегося). Поэмы «Облако в штанах», «Во весь голос».
А.А. Фадеев. «Разгром».
М.А. Булгаков. «Мастер и Маргарита» или другое по выбору произведение.
А.Н. Толстой. «Петр 1».
М.А Шолохов. «Тихий Дон» или «Поднятая целина».
Великая Отечественная война в литературе 40-х и последующих лет (2 – 3 произведения по выбору).
2 – 3 произведения современной русской литературы (по выбору учащегося).
Список литературных произведений для приёма экзаменов от лиц, окончивших национальную школу.
А.С. Пушкин. Избранная лирика («К Чаадаеву», «Я памятник себе воздвиг...» и др.). Общая характеристика романа «Евгений Онегин».
М.Ю. Лермонтов. «Смерть поэта», «Княжна Мери», избранная лирика по выбору абитуриента.
Н.В. Гоголь. «Ревизор».
Н.А. Некрасов. «Железная дорога», «Мороз, Красный нос».
Л.Н. Толстой. «После бала». Общая характеристика романа «Война и мир».
А.П. Чехов. «Хамелеон», «Человек в футляре».
A.M. Горький. «Мать», «Старуха Изергиль».
В.В. Маяковский. «Во весь голос».
М.А. Шолохов. «Судьба человека».
A.T. Твардовский. «Василий Теркин».
К.Г. Паустовский. «Телеграмма», рассказы по выбору абитуриента.
^ ПРИМЕРНЫЕ ТЕМЫ СОЧИНЕНИЙ НА ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНАХ.
1. Идеал человека в представлении фамусовского общества и Чацкого.
2. «И долго буду тем любезен я народу, что чувства добрые я лирой пробуждал» (А.С Пушкин).
3. Лирика М.Ю. Лермонтова.
4. Изображение помещиков в поэме Н.В. Гоголя «Мертвые души».
5. Герой романа И.А Гончарова «Обломов».
- «Гроза» - самое решительное, произведение А.Н.Островского (Н.А. Добролюбов).
- Павел Петрович Кирсанов и Е.Базаров в романе Тургенева «Отцы и дети».
8. Особенный человек Рахметов (роман «Что делать?» Н.Г.Чернышевского).
9. Н.А.Некрасов – поэт крестьянской демократии.
10. «Я лиру посвятил народу своему» (Н.А. Некрасов).
11. Положение крестьян по поэме Н.А. Некрасова «Кому на Руси жить хорошо».
12. Петербург в изображении Достоевского («Преступление и наказание»).
13. Изображение войны 1812 года в романе Л.Н. Толстого «Война и мир».
- Любимые герои Л.Н. Толстого в романе «Война и мир».
- Поиски смысла жизни передовой дворянской интеллигенции в романе Л.Н. Толстого «Война и мир».
16. История нравственного падения доктора Старцева (рассказ А.П. Чехова «Ионыч»).
17. Изображение трех действительностей в пьесе А. П.Чехова «Вишневый сад».
I8. Новаторство в изображении человека (по творчеству М. Горького)
19. Тема гуманизма и милосердая в пьесе М. Горького «На дне».
20. Изображение Родины в творчестве А.А. Блока.
21. Изображение Родины в творчестве С.А. Есенина.
22. Поэма «Емельян Пугачев» С.А. Есенина.
23. Изображение гражданской войны в литературе.
24. Изображение подвига народа в произведениях современной литературы.
25. Тема экологии в произведениях современной литературы.
- Герой войны – герой литературы.
- Герой труда – герой литературы.
- Наш современник в произведениях литературы.
^ ПРОГРАММА ПО МАТЕМАТИКЕ.
Общие положения.
Приведенные ниже требования к математической подготовке поступающих в средние специальные учебные заведения согласованы с итоговыми требованиями начальной и старшей школы, зафиксированными Временным государственным стандартом в образовательной области «Математика».
Содержание программы сгруппировано вокруг стержневых линий школьного курса математики: «Числа и вычисления», «Выражения и их преобразования», «Уравнения и неравенства», «Функция», «Геометрические фигуры. Измерение геометрических величин».
На экзамене по математике поступающие в средние специальные учебные заведения должны:
1) знать определение математических понятий, формулировки основных теорем, основные формулы;
- уметь доказывать теоремы и выводить формулы, проводить доказательные рассуждения в ходе решения задач в устном и письменном изложении;
- владеть основными умениями и навыками, предусмотренными программой, уметь решать типовые задачи.
Программа по математике для поступающих в средние специальные учебные заведения содержит три раздела.
Первый раздел состоит из перечня основных понятий и фактов, которые должны знать поступающие и уметь применять, т. е. ссылаться на них при доказательстве теорем и выводе формул, использовать их при решении задач.
Во втором разделе указаны теоремы и формулы, которые надо уметь формулировать и доказывать. Из вопросов этого раздела формируется содержание теоретической части экзамена.
В третьем разделе перечислены основные умения и навыки, которыми должны владеть поступающие.
Раздел 1. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ^ ПОНЯТИЯ И ФАКТЫ
Числа и вычисления.
1. Натуральные числа. Простые и составные числа. Делитель, кратное. Разложение натурального числа на простые множители. Наибольший общий делитель, наименьшее общее кратное.
2. Признаки делимости на 2, 5, 10, 3 и 9.
- Целые числа. Рациональные числа, их сложение, вычитание, умножение и деление. Сравнение рациональных чисел.
- Действительные числа, их представление в виде десятичных дробей.
- Числовая прямая. Модуль числа, его геометрический смысл.
Выражения и их преобразования.
1. Числовые выражения. Тождественные преобразования. Выражения с переменными. Формулы сокращенного умножения.
2. Степень с натуральным и рациональным показателем. Арифметический корень.
3. Одночлен и многочлен. Степень многочлена. Разложение многочлена на множители.
4. Квадратный трёхчлен. Разложение квадратного трехчлена на множители.
5. Основные тригонометрические тождества. Формулы приведения. Синус и косинус суммы и разности двух углов. Синус и косинус двойного угла. Тождественные преобразования
тригонометрических выражений.
- Арифметическая прогрессия. Формулы n-го члена и суммы n первых ее членов.
- Геометрическая прогрессия. Формулы n-го члена и суммы n первых её членов.
- Логарифмы, их свойства.
Уравнения.
- Уравнение. Корни уравнения. Равносильность. Неравенства. Решения неравенств.
- Линейные уравнения с одним неизвестным.
- Квадратные уравнения. Формулы корней.
4. Система уравнений. Решение системы двух линейных уравнений с двумя неизвестными и его геометрическая интерпретация.
5. Линейное неравенство с одним неизвестным. Система линейных неравенств с одним неизвестным.
6. Неравенства второй степени с одним неизвестным.
7. Формулы решения простейших тригонометрических уравнений.
8. Простейшие показательные уравнения и неравенства.
9. Простейшие логарифмические уравнения и неравенства.
Функции.
1. Функция. Способы задания функции. Область определения. Множество значений функции. График функции. Возрастание и убывание функций, сохранение знака. Четные и нечётные функции. Периодические функции.
2. Линейная, квадратичная, степенная, показательная, логарифмическая, тригонометрические функции. Их свойства и графики. Понятие" об обратной функции.
3. Тригонометрические функции: синус, косинус, тангенс. Их свойства и графики.
4. Производная. Её геометрический и физический смысл.
Геометрические фигуры. Измерение геометрических величин.
1. Вертикальные и смежные углы и их свойства.
- Параллельные прямые, перпендикулярные прямые на плоскости.
- Треугольник. Медиана, биссектриса, высота. Виды треугольников. Соотношение между сторонами и углами прямоугольного треугольника. Теорема Пифагора.
4. Признаки равенства треугольников.
5. Сумма углов треугольника.
6. Признаки подобия треугольников.
7. Четырехугольники: параллелограмм, прямоугольник, ромб, квадрат, трапеция.
8. Окружность и круг. Центр, хорда, диаметр, радиус, дуга. Касательная к окружности.
9. Формулы площади треугольника, прямоугольника, параллелограмма, ромба, квадрата, трапеции.
10. Градусная и радианная меры угла.
11. Длина окружности, длина дуги окружности.
12. Площадь круга, площадь сектора.
13. Подобные фигуры. Отношение площадей подобных фигур.
14. Параллельные прямые в пространстве. Скрещивающиеся прямые. Параллельные и пересекающиеся прямые.
15. Прямая, параллельная плоскости. Признак параллельности прямой плоскости.
16. Параллельные плоскости. Признак параллельности плоскостей.
17. Теорема о пресечении двух параллельных плоскостей третьей.
18. Перпендикуляр к плоскости. Наклонная, проекция наклонной.
19. Признак перпендикулярности прямой к плоскости.
20. Теорема о трех перпендикулярах.
- Перпендикулярность плоскостей. Признак перпендикулярности плоскостей.
- Угол между прямой и плоскостью.
23. Двугранный угол. Линейный угол двугранного угла.
24. Призма, её элементы. Формулы площади боковой поверхности и объема призмы.
25. Пирамида, её элементы. Формулы площади поверхности и объёма пирамиды.
26. Тела вращения. Цилиндр. Формулы площади поверхности и объема цилиндра.
27. Конус. Формулы площади поверхности и объема конуса.
28. Шар. Формулы площади поверхности и объема.
Раздел 2. ОСНОВНЫЕ ^ ФАКТЫ, ФОРМУЛЫ И ТЕОРЕМЫ.
Алгебра и начала анализа.
- Функция у = kx, ее свойства и график.
- Функция у =
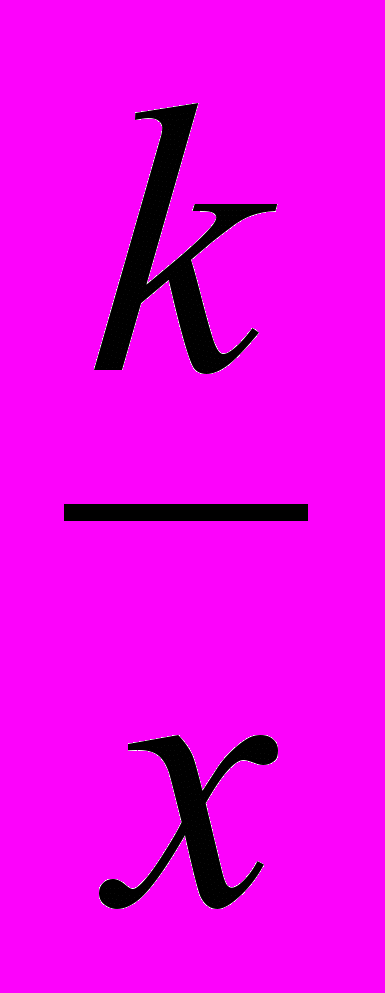 , ее свойства и график.
, ее свойства и график.
- Функция у = kx + b, ее свойства и график.
- Квадратичная функция, ее свойства и график.
- Квадратное уравнение и его решение. Формулы корней квадратного уравнения.
- Квадратный трехчлен и его разложение на множители.
- Числовые неравенства и их свойства.
8. Линейное неравенство и его решение. Системы линейных неравенств, их решение (на конкретных примерах).
9. Логарифмы и их свойства.
10. Функция синус и косинус, их свойства и графики.
11. Функция тангенс, ее свойства к график.
12. Решение уравнений вида sin х = a, cos x = a, tg x = а.
13.Формулы приведения.
- Зависимости между тригонометрическими функциями одного и того же аргумента.
- Синус и косинус суммы и разности двух аргументов.
- Синус и косинус двойного аргумента.
- Производная и ее геометрический смысл.
- Производная функции.
- Производная суммы двух функций.
Геометрия.
- Свойство равнобедренного треугольника.
- Свойство серединного перпендикуляра к отрезку.
- Признаки параллельности прямых на плоскости.
- Теорема о сумме углов треугольника.
- Признаки параллелограмм. Свойства параллелограмма.
- Окружность, описанная около треугольника.
- Окружность, вписанная в треугольник.
- Касательная к окружности, ее свойства.
- Теорема о вписанном угле в окружность.
10. Признаки подобия треугольников.
11. Теорема Пифагора.
12. Формулы площадей параллелограмма, треугольника, трапеции.
- Признак параллельности прямой и плоскости.
- Признак параллельности плоскостей.
- Признак перпендикулярности прямой и плоскости.
- Теорема о трех перпендикулярах.
- Признак перпендикулярности двух плоскостей.
- Теорема о боковой поверхности правильной пирамиды.
- Формулы для вычисления объема и площади поверхности прямоугольного параллелепипеда, призмы, пирамиды, цилиндра, конуса, шара.
Раздел 3. ОСНОВНЫЕ УМЕНИЯ И НАВЫКИ.
Поступающие должны:
- Уверенно выполнять арифметические действия над числами; с требуемой точностью округлять данные числа и результаты вычислений; пользоваться калькулятором.
- Решать основные задачи на дроби и проценты, составлять и решать пропорции.
3. Выполнять тождественные преобразования рациональных выражений, используя разложения многочленов на множители, формулы сокращенного умножения, формулы, связанные со свойствами степеней; логарифмов, показательной и тригонометрических функций.
- Владеть общими приемами решений уравнений и систем уравнений.
- Решать неравенства и уравнения первой и второй степени; уравнения, сводящиеся к ним; решать несложные системы уравнений первой и второй степени.
6. Решать несложные показательные, логарифмические, тригонометрические уравнения, простейшие неравенства.
7. Уметь пользоваться методом интервалов для решения несложных рациональных неравенств.
8. Свободно «читать» графики, отражать свойства функций на графике (монотонность, сохранение знака, экстремумы, наибольшее и наименьшее значение, ограниченность, периодичность).
9. Определять значение функции по значению аргумента при любом способе задания функции, применяя при необходимости вычислительную технику,
10. Владеть свойствами тригонометрических, показательных, логарифмических и степенных функций, изображать их графики, описывать свойства этих функций, опираясь на графики; уметь
использовать свойства функций для сравнения и оценки её значений.
11. Находить производные элементарных функций, пользуясь таблицей производных и правилами дифференцирования суммы и произведения.
12. Применять производную дня исследования функций в несложных ситуациях на монотонность, экстремумы, для нахождения наибольшего и наименьшего значений функций, в
том числе для построения графиков функций.
13. Находить в простейших случаях первообразные функции, применять первообразную для нахождения площадей криволинейных трапеций.
14. Изображать геометрические фигуры на чертеже, иллюстрировать чертежом условие несложной стереометрической задачи.
15. Решать несложные задачи на вычисление геометрических величин (длин отрезков, углов, площадей, объемов) с использованием свойств геометрических фигур и формул.
