Системные технологии
| Вид материала | Анализ |
СодержаниеАктуальность темы. Анализ последних исследований. Обоснование полученных результатов |
- Системные технологии, 124.36kb.
- 004 Информационные технологии. Компьютерные технологии, 935.71kb.
- Методология научного исследования, 1482.66kb.
- Курс предназначен для it-специалистов следующих категорий: системные администраторы, 67.72kb.
- Системные технологии, 99.4kb.
- Окружающего мира подразумевает разделение материи по уровням масштабности и изучение, 430.62kb.
- Системные биомаркеры сыворотки крови у больных хронической обструктивной болезнью легких, 303.23kb.
- Технология проведения инвестиционных и спекулятивных операций на рынке гко/офз/обр, 186.43kb.
- В. В. Глущенко. Менеджмент. Системные основы. Издание 2-е. М.; Нпц крылья, 1998., 3141.52kb.
- Доклад на тему: «Здоровьесберегающие технологии в школе», 39.98kb.
5(64) 2009 «Системные технологии»
УДК 62-50:519.49
В.М. Григорьев
ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ МАТРИЧНЫЕ ОПЕРАТОРНЫЕ УРАВНЕНИЯ
Получены конструктивные процедуры решения однородных и неоднородных линейных нестационарных дифференциальных матричных операторных уравнений, основанные на приведении матриц к треугольным формам, которое может осуществляться с помощью систем компьютерной алгебры Maple, Reduce, Singular, Gap и т.д.
Ключевые слова: линейные нестационарные дифференциальные матричные операторные уравнения, приведение матрицы к треугольной форме, Maple, Reduce, Singular, Gap.
^ Актуальность темы. Широкий класс объектов и систем управления адекватно представляются в виде системы линейных нестационарных дифференциальных уравнений с производными в правой части. Математическая теория линейных нестационарных многосвязных систем автоматического регулирования основывается либо на использовании методов пространства состояний [1], либо на применении теории матриц над некоммутативным кольцом линейных нестационарных дифференциальных операторов [2]. В рамках операторного подхода анализ и синтез линейных нестационарные систем осуществляется путём решения линейных матричных операторных уравнений.
^ Анализ последних исследований. Теоретическим основанием работы является линейная алгебра над некоммутативными кольцами [3]
Постановка задачи. Цель работы состоит в получении конструктивных процедур решения однородных и неоднородных линейных нестационарных дифференциальных матричных операторных уравнений.
^ Обоснование полученных результатов. Рассмотрим кольцо R линейных нестационарных дифференциальных операторов с коэффициентами из произвольного поля функций Q, замкнутого относительно дифференцирования. Операторы действуют в пространстве сигналов, состоящем из бесконечнодифференцируемых, за исключением конечного числа точек, функций [4].
Григорьев В.М., 2009
Рассмотрим матрицы Al
 Rn
Rn n, Bl
n, Bl  Rn
Rn m (Ar
m (Ar  Rm
Rm m, Br
m, Br  Rn
Rn m). Следуя [5], приведём c помощью элементарных столбцовых (строчных) операций
m). Следуя [5], приведём c помощью элементарных столбцовых (строчных) операцийматрицу E = |Al Bl| (E =
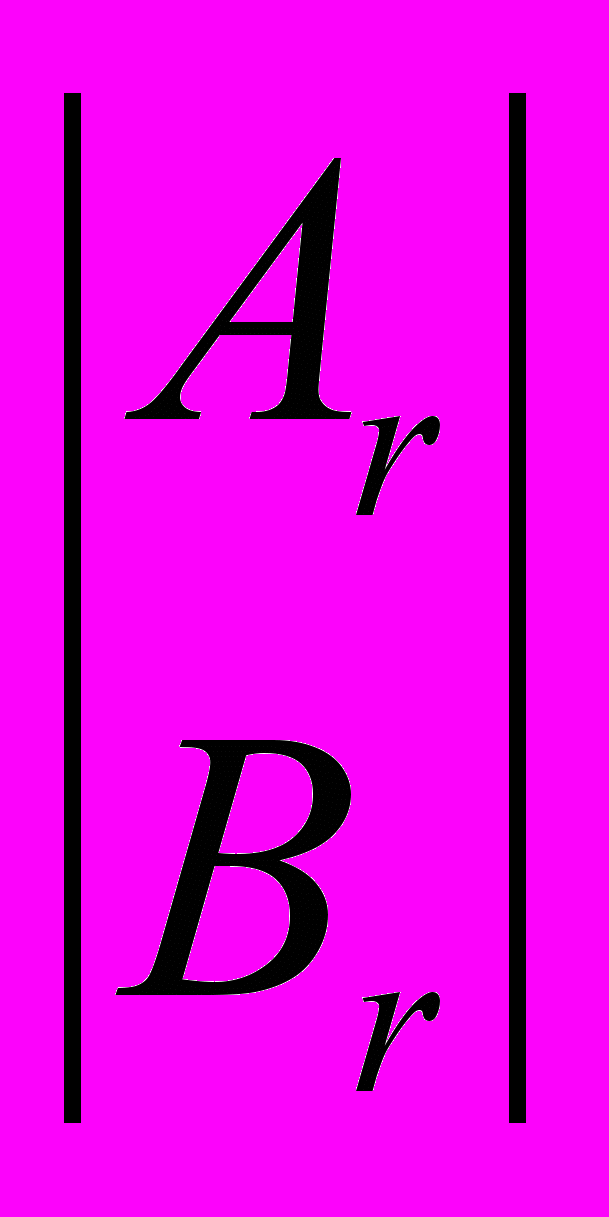 ) к нижней левой (верхней правой) ступенчатой матрице. Используя следствие из [5], имеем
) к нижней левой (верхней правой) ступенчатой матрице. Используя следствие из [5], имеем EU = | Сl 0n
 m | (UE =
m | (UE = 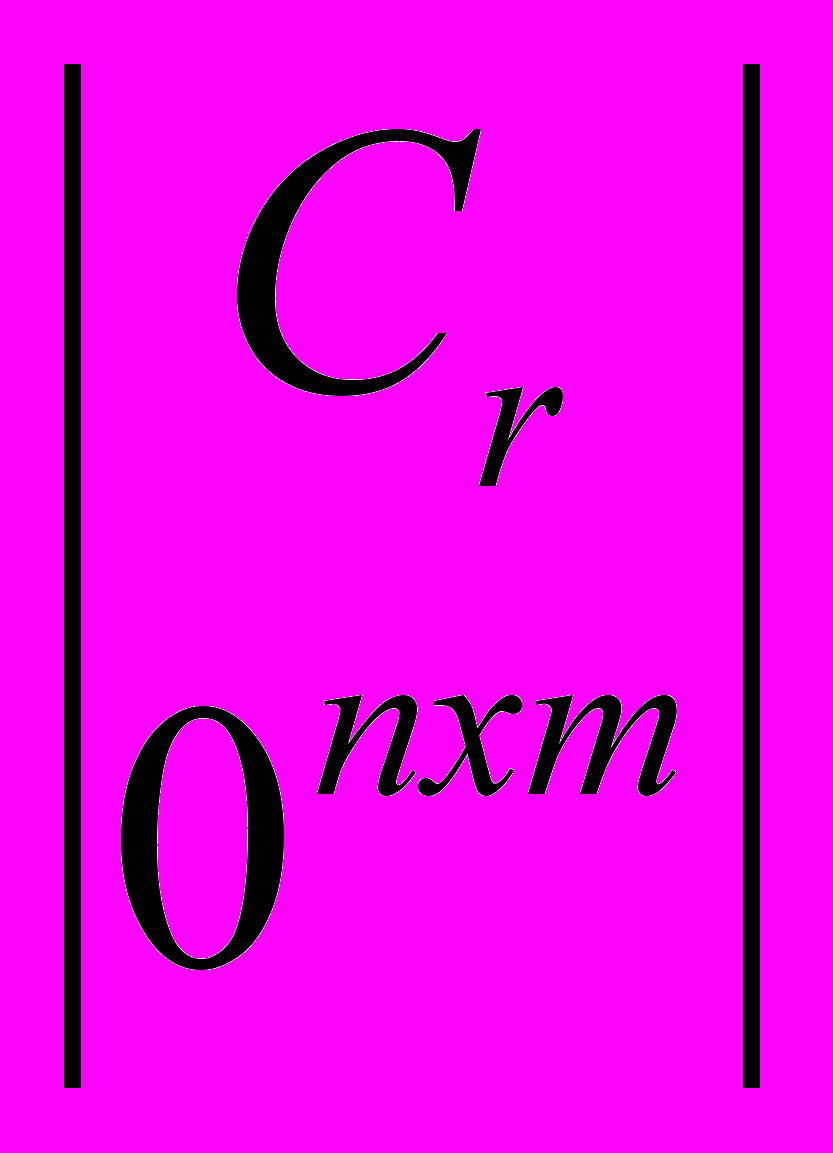 ), (1)
), (1)где U, U-1
 R(n+m)
R(n+m) (n+m), Сl
(n+m), Сl Rn
Rn n ( Сr
n ( Сr Rm
Rm m).
m). Согласно работе [6], матрица Сl (Сr) в (1) является левым (правым) наибольшим общим делителем ЛНОД (ПНОД) матриц Al и Bl (Ar и Br). Обозначим
U-1 =
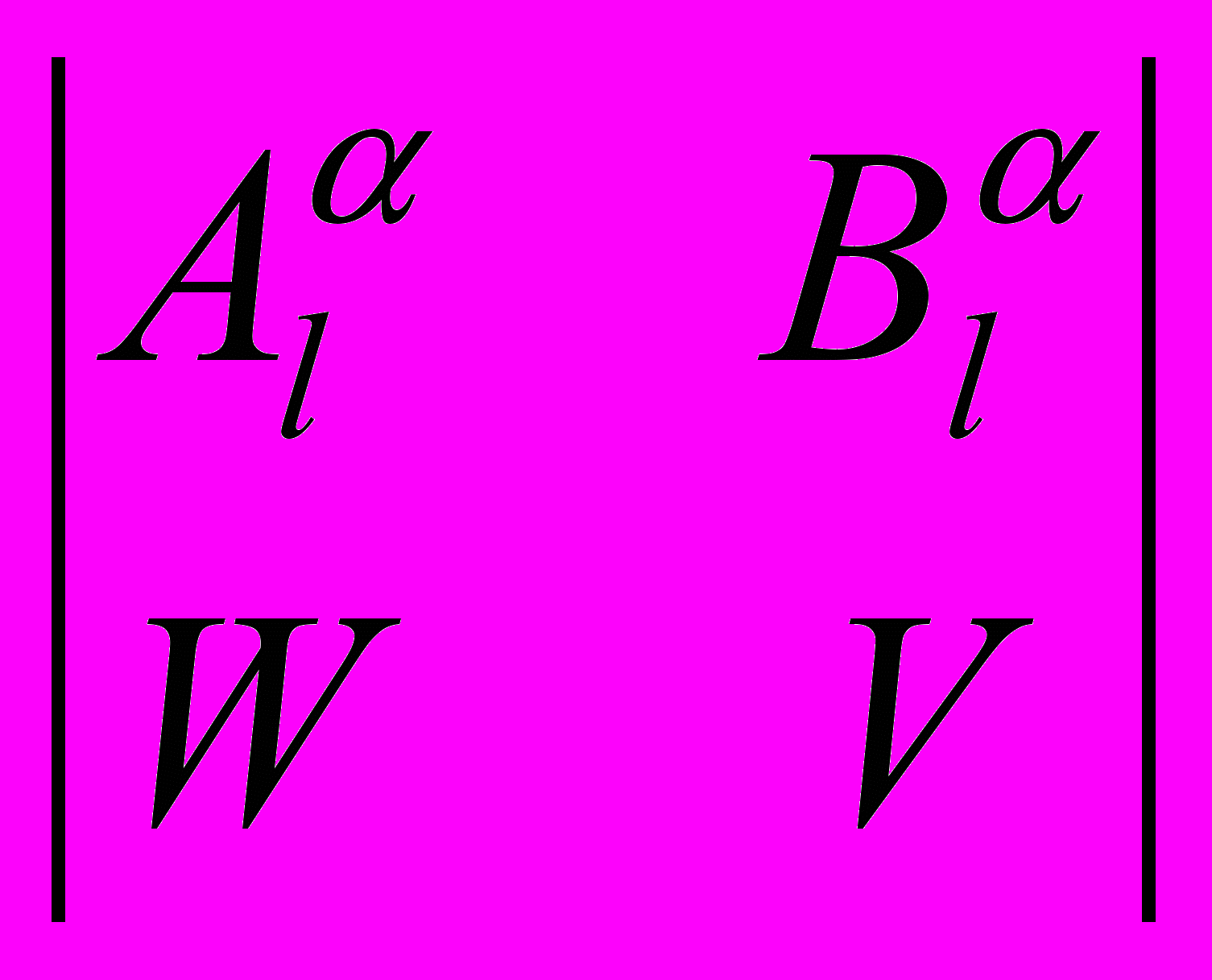 , (U-1 =
, (U-1 = 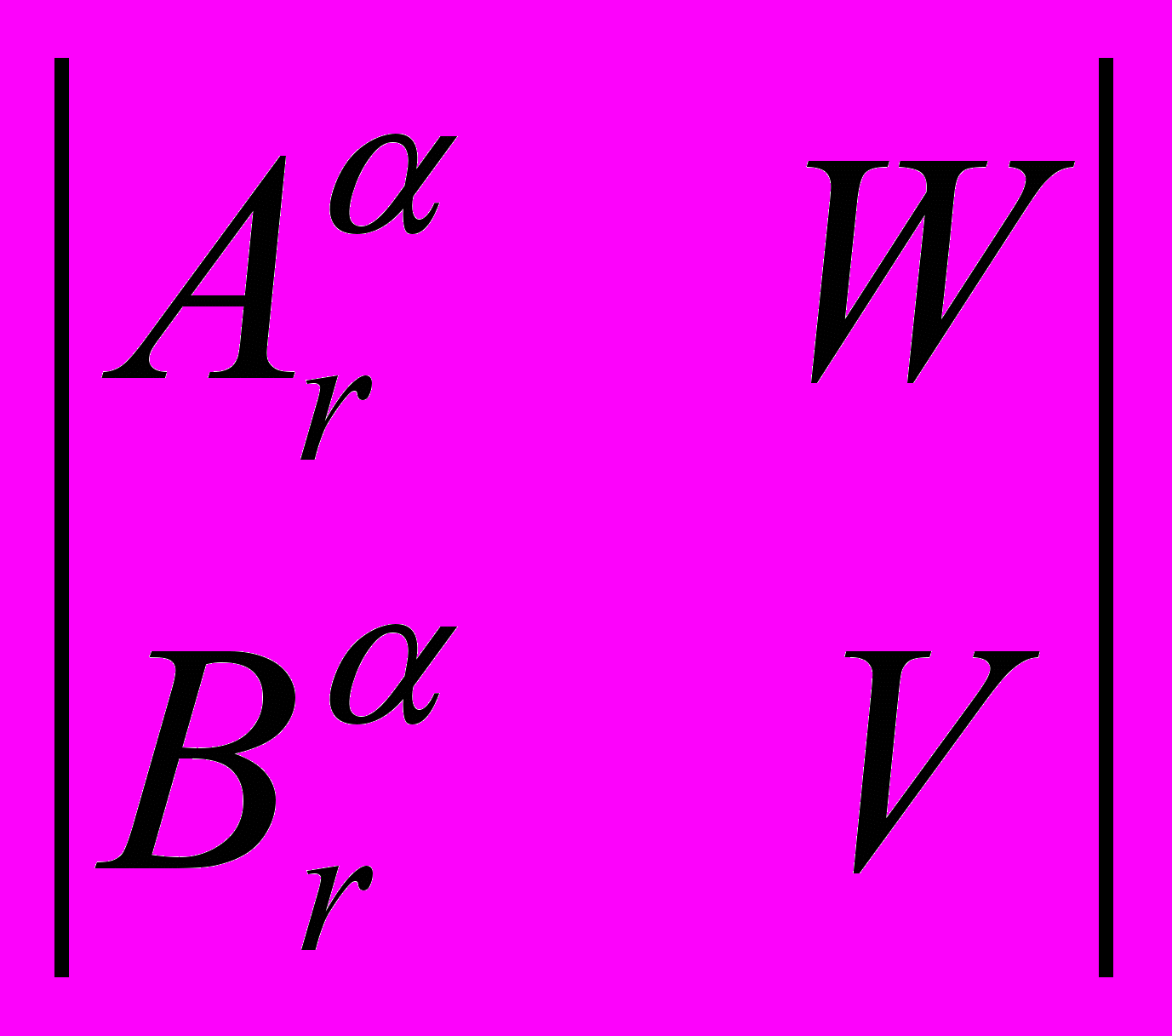 ), (2)
), (2)U =
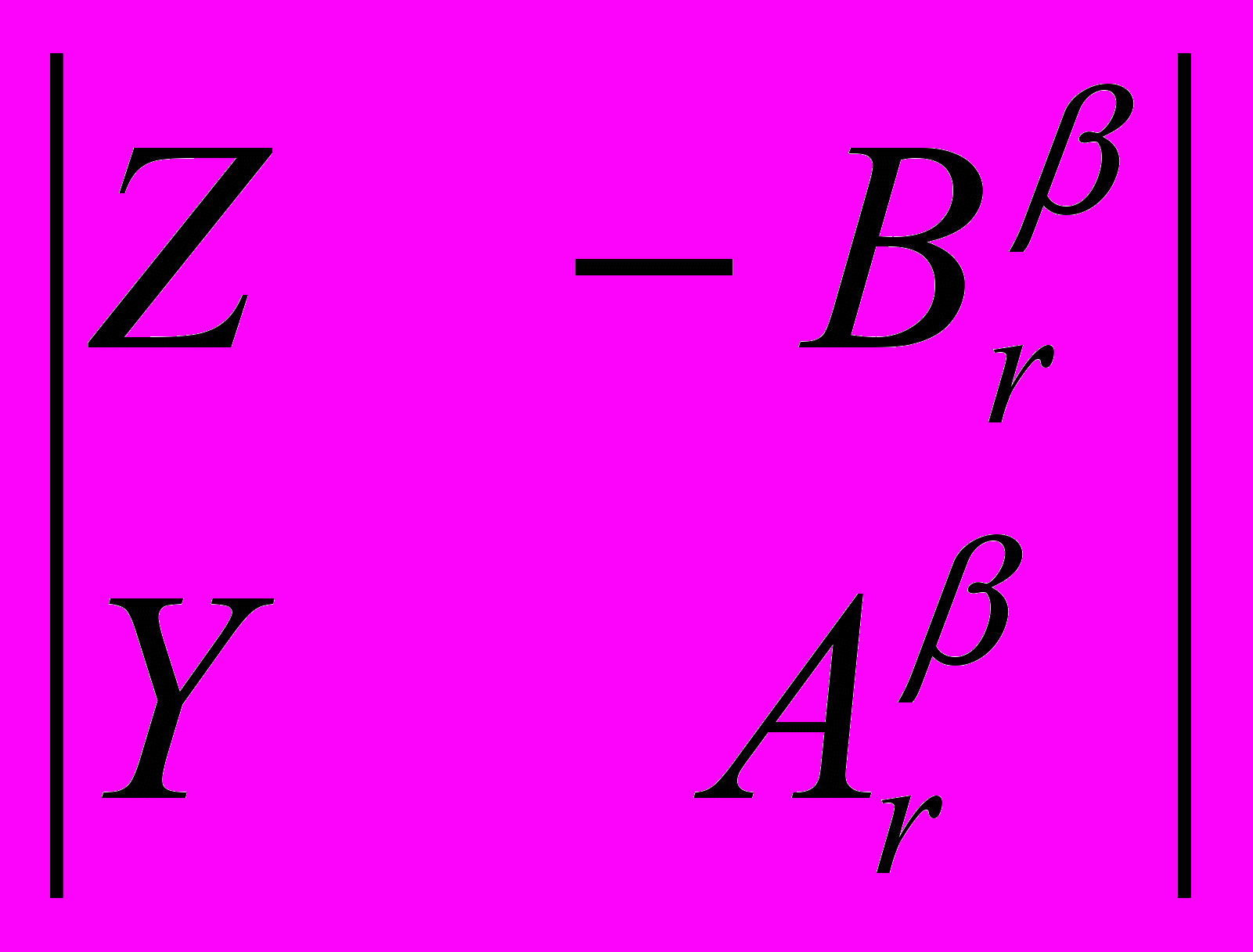 , (U =
, (U = 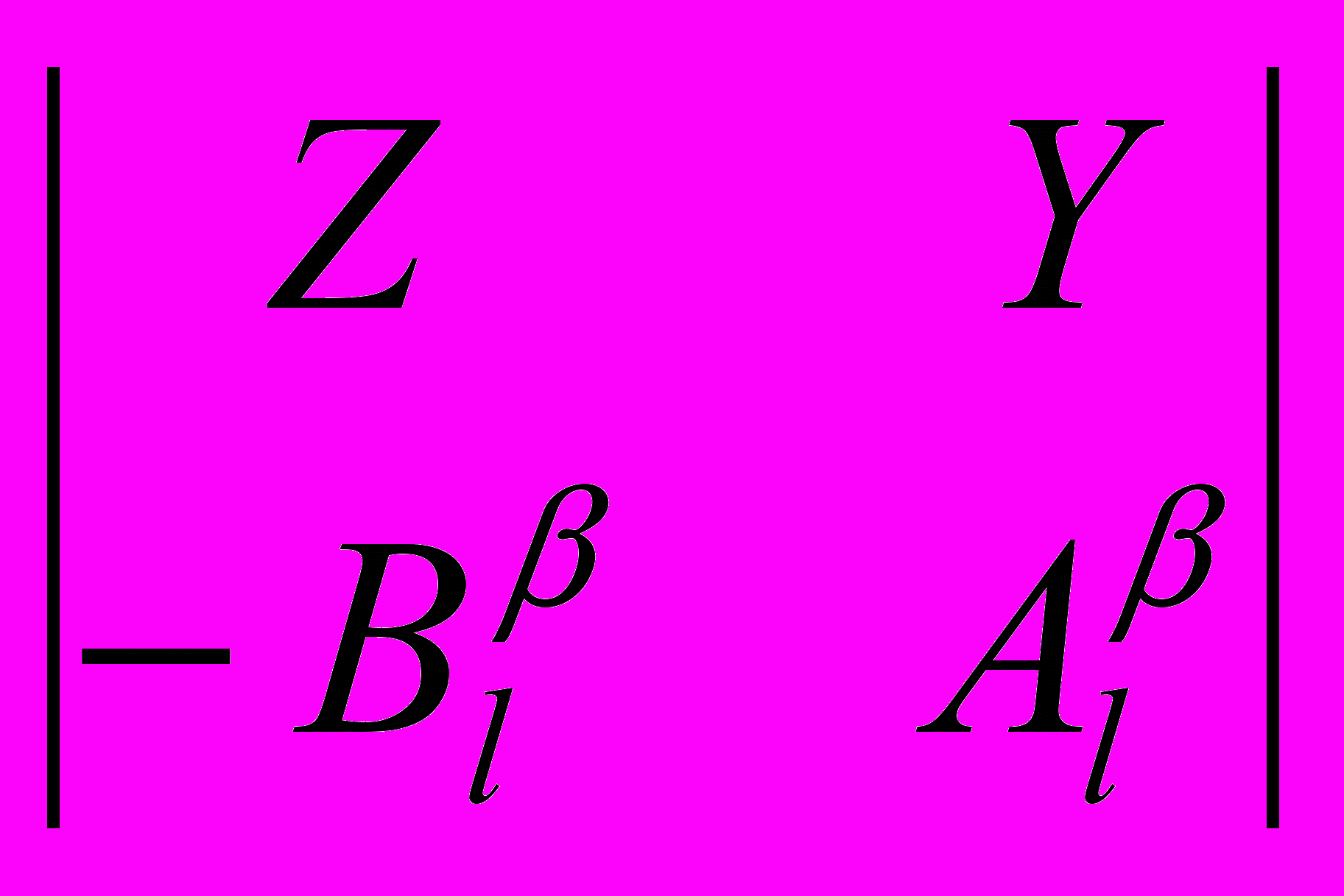 ), (3)
), (3)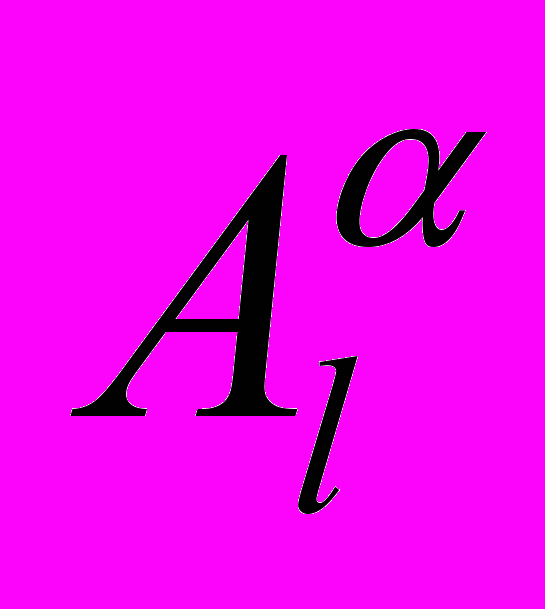
 Rn
Rn n,
n, 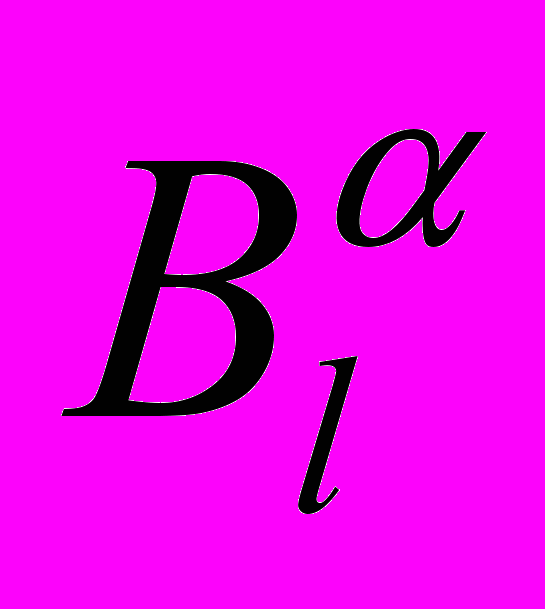
 Rn
Rn m, W
m, W Rm
Rm n, V
n, V Rm
Rm m,
m,Z
 Rn
Rn n,
n, 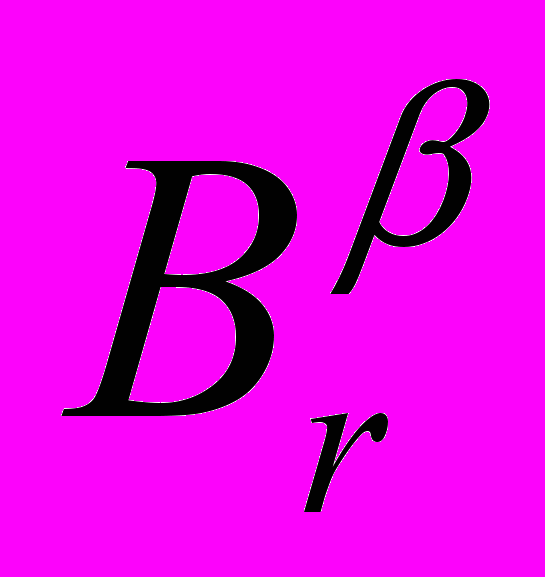
 Rn
Rn m, Y
m, Y Rm
Rm n,
n, 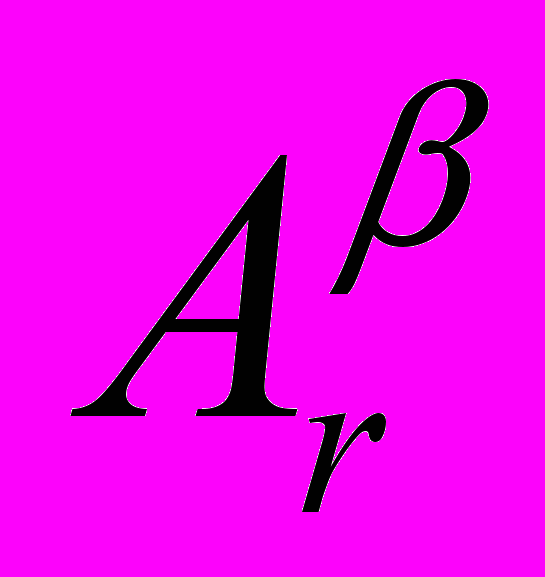
 Rm
Rm m.
m.(
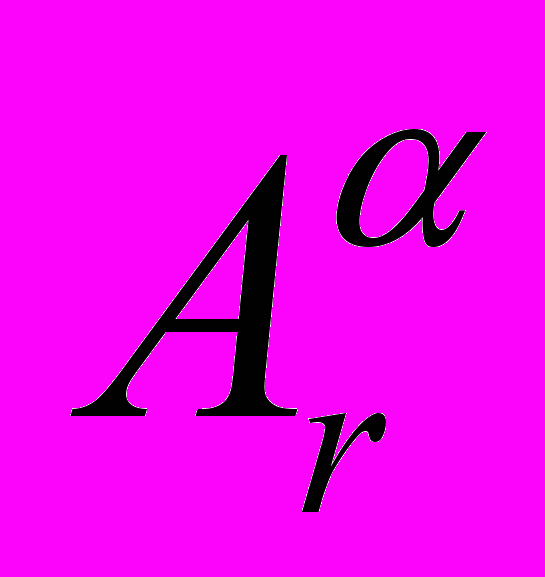
 Rm
Rm m, W
m, W Rm
Rm n,
n, 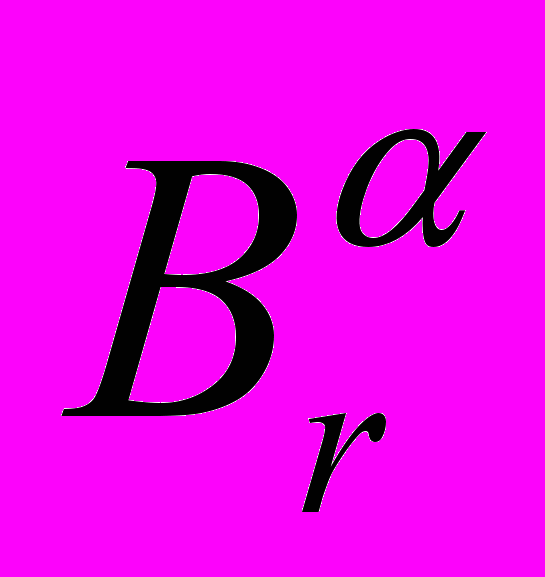
 Rn
Rn m, V
m, V Rn
Rn n,
n,Z
 Rm
Rm m, Y
m, Y Rm
Rm n,
n, 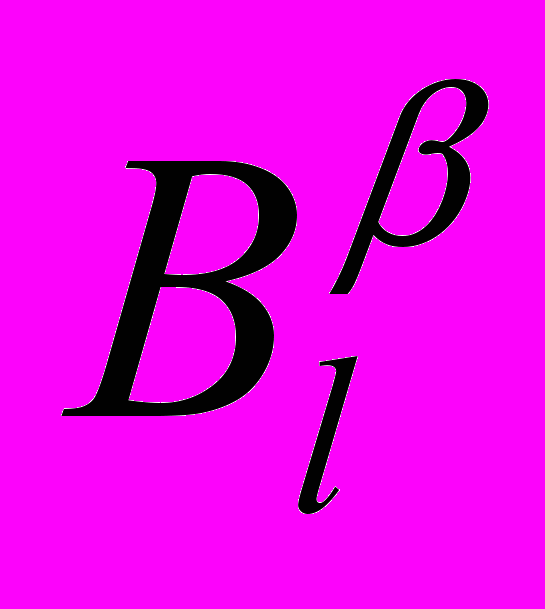
 Rn
Rn m,
m, 
 Rn
Rn n).
n).Умножая (1) справа (слева) на матрицу U-1, получим
Al = Сl
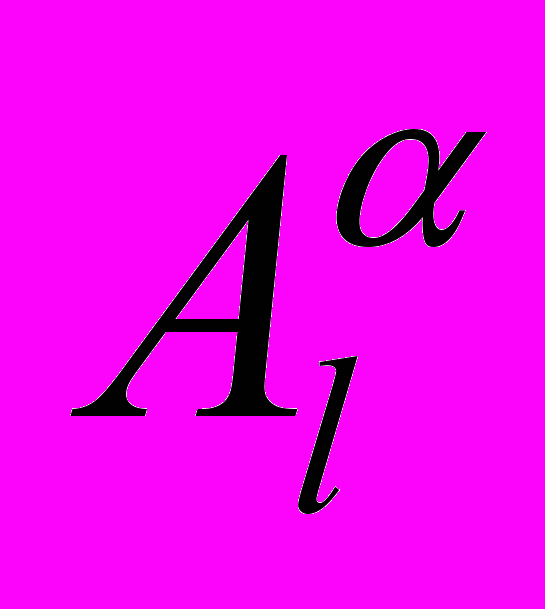 , Bl= Сl
, Bl= Сl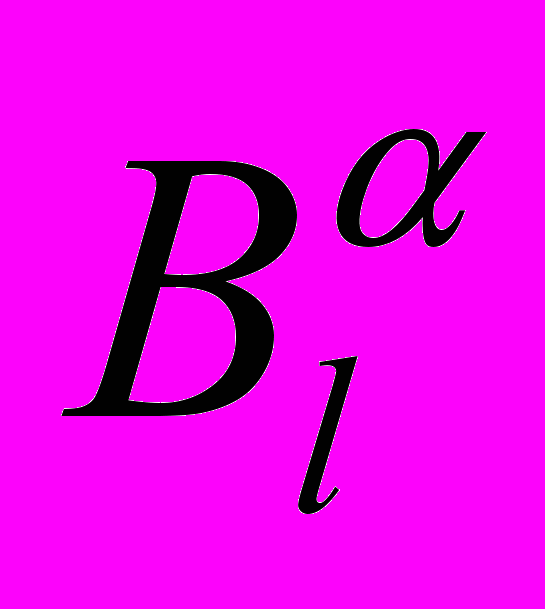 (4)
(4)(Ar =
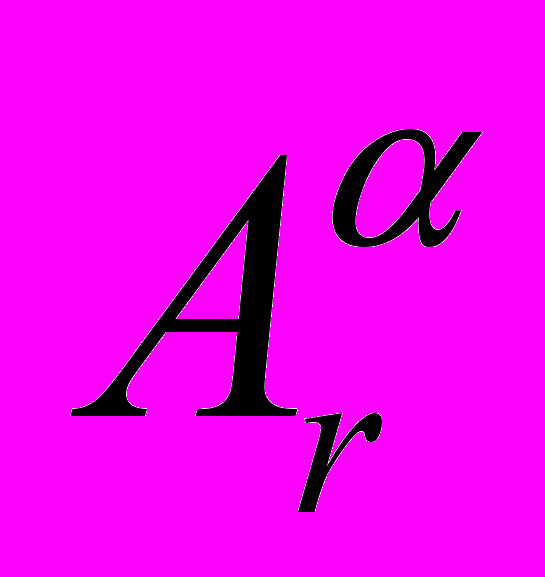 Сr, Bl=
Сr, Bl= 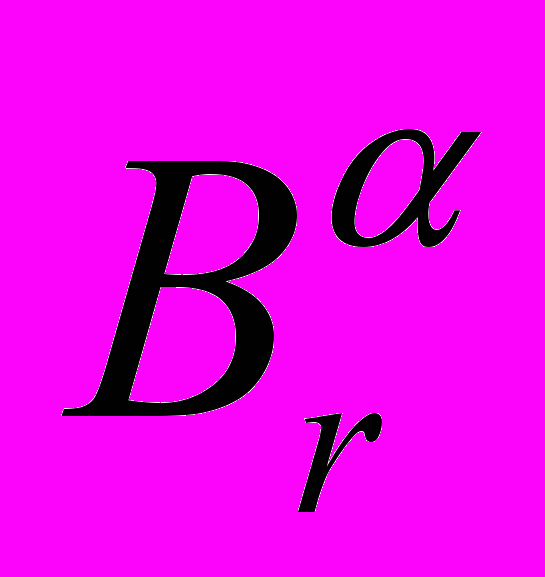 Сr)
Сr)Рассмотрим однородное матричное уравнение
Alz + Bly= 0n
 k (zAr+ yBr=0k
k (zAr+ yBr=0k m) (5)
m) (5)относительно неизвестных матриц z
 Rn
Rn k, y
k, y  Rm
Rm k (z
k (z Rk
Rk m, y
m, y Rk
Rk n).
n).Из соотношения (1) с учётом обозначений (3), получаем частное решение уравнения (5) при k=m (k=n)
z = -
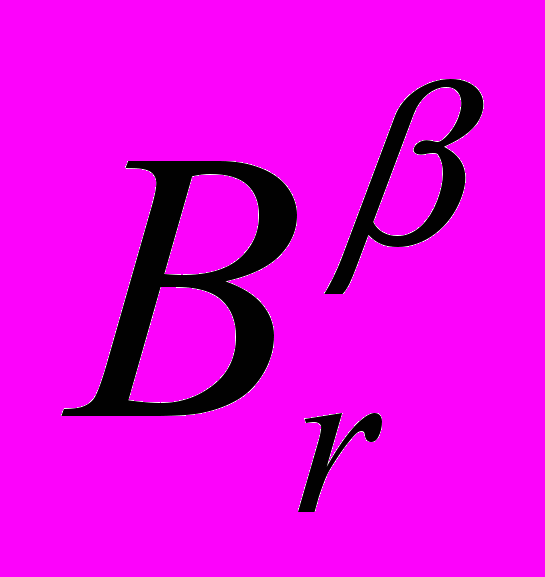 , y =
, y = 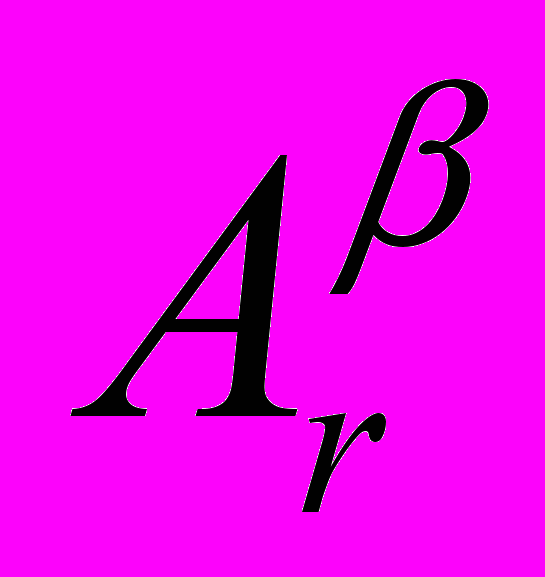 (z = -
(z = -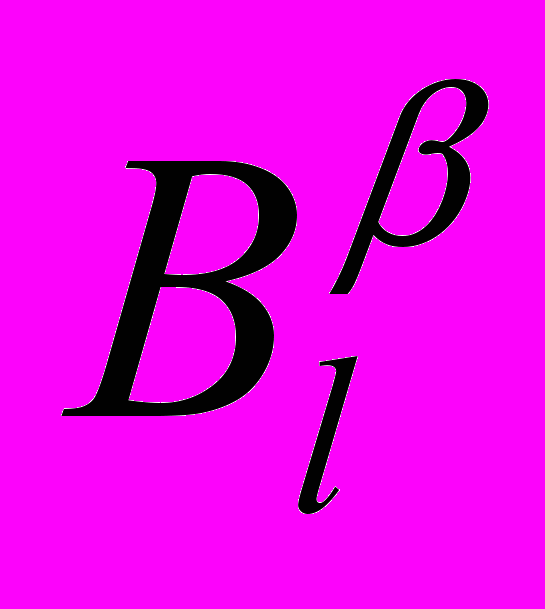 , y =
, y =  ) (6)
) (6)Из обозначений (2) и (3) и соотношения U-1U = In+m (UU-1 = In+m), следует, что -W
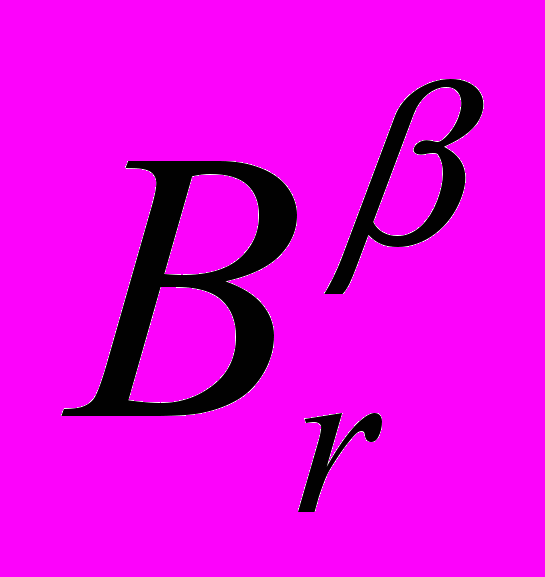 +V
+V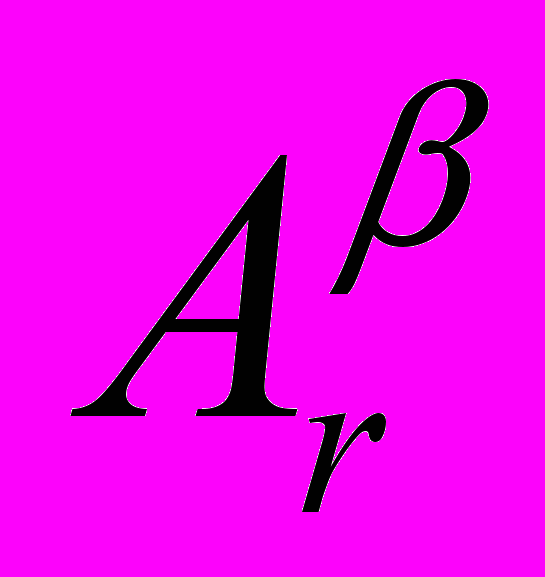 = Im (-
= Im (-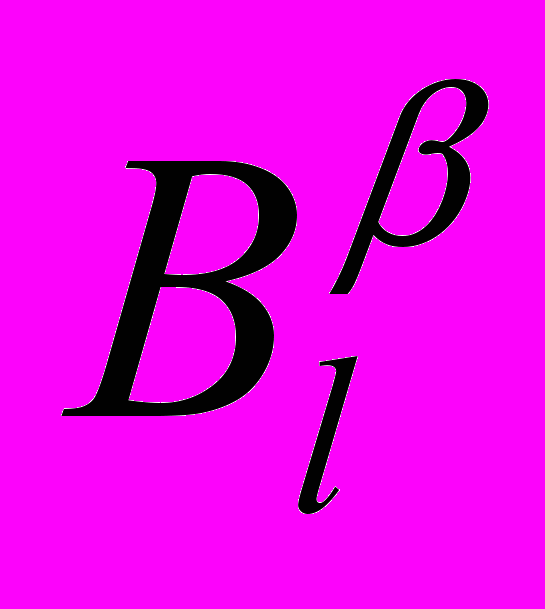 W+
W+ V= In). Согласно работе [6], это означает, что матрицы
V= In). Согласно работе [6], это означает, что матрицы 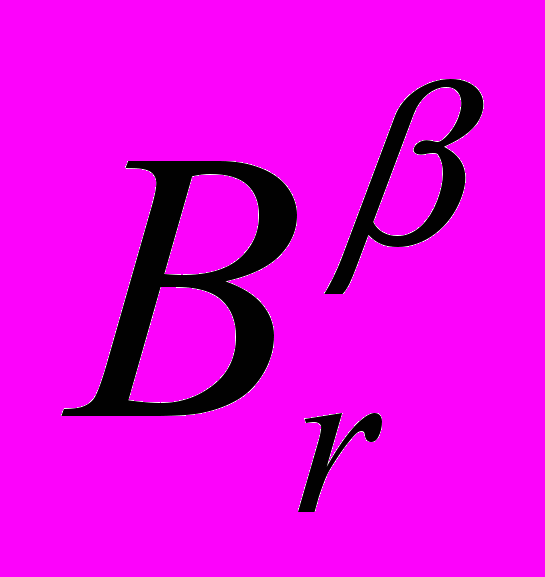 и
и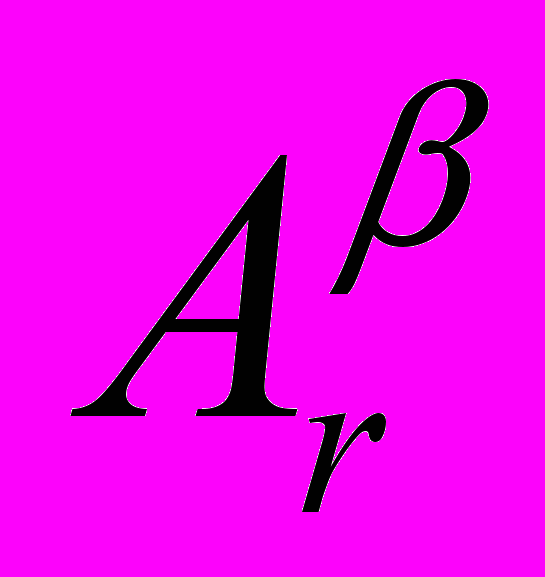 (
(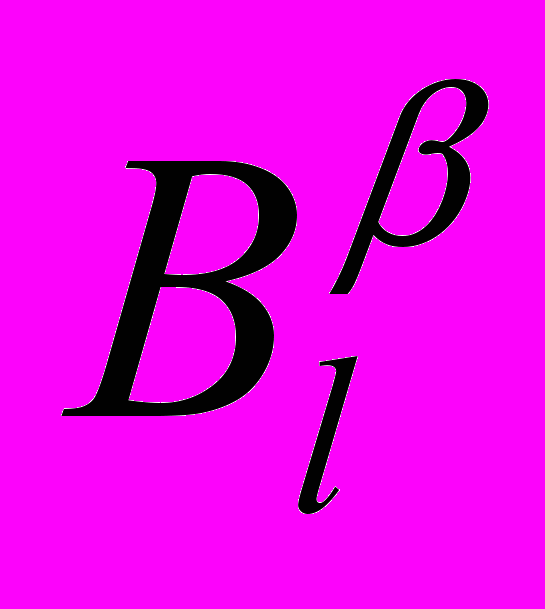 и
и ) взаимно просты справа (слева).
) взаимно просты справа (слева).Для любой матрицы T из Rm
 k (Rk
k (Rk n) матрицы
n) матрицыz =
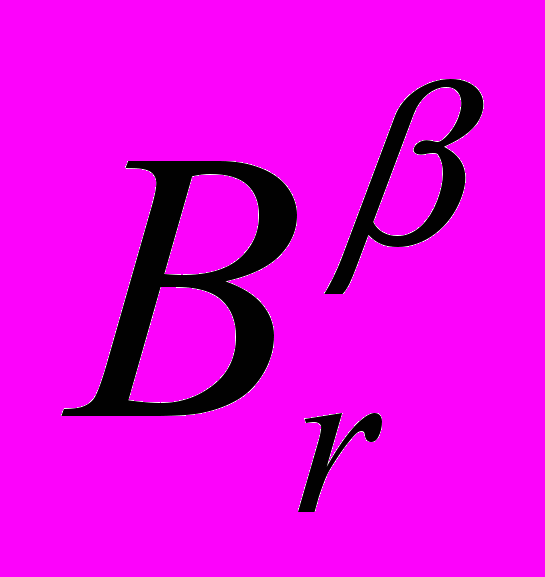 T, y =
T, y = 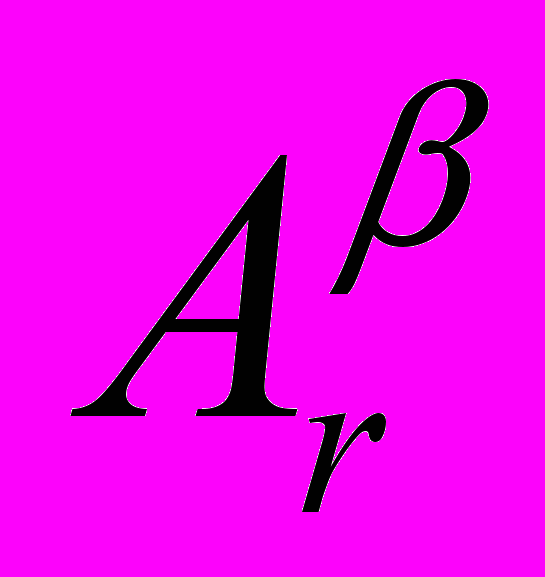 T (z = T
T (z = T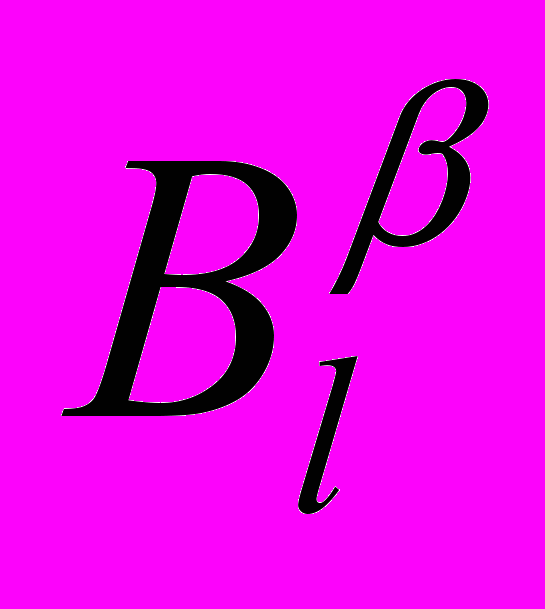 , y = T
, y = T  ) (7)
) (7)являются решением уравнения (5) для любого натурального числа k.
Предложение 1. Если в уравнении (5) матрица Al (Ar) имеет полный ранг, то его общее решение имеет вид (7).
Доказательство. Пусть z и y – произвольное решение уравнения (5). Учитывая (1) и (2), совершим ряд преобразований
0 n
 k = |Al Bl|
k = |Al Bl| 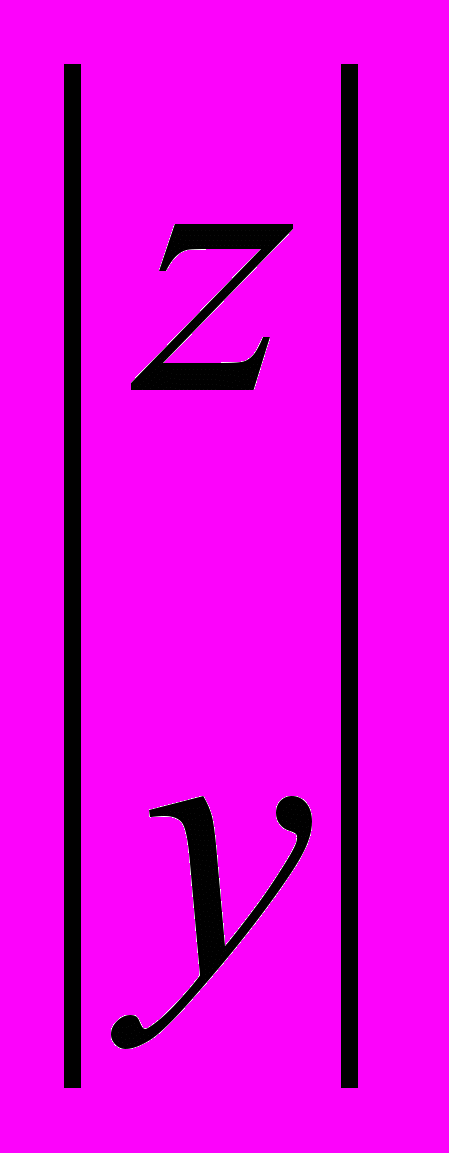 = |Al Bl| U U-1
= |Al Bl| U U-1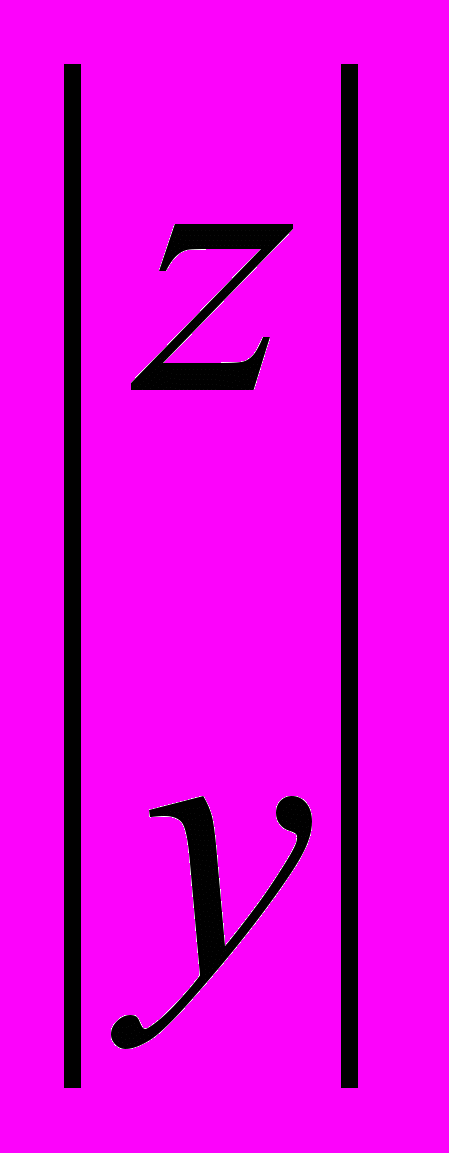 = | Сl 0n
= | Сl 0n m |
m | 
или
Сl
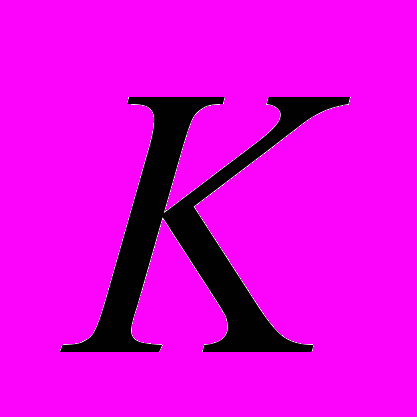 = 0 n
= 0 n k, (8)
k, (8)где
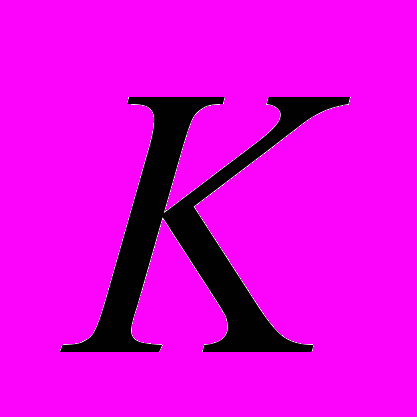 =
=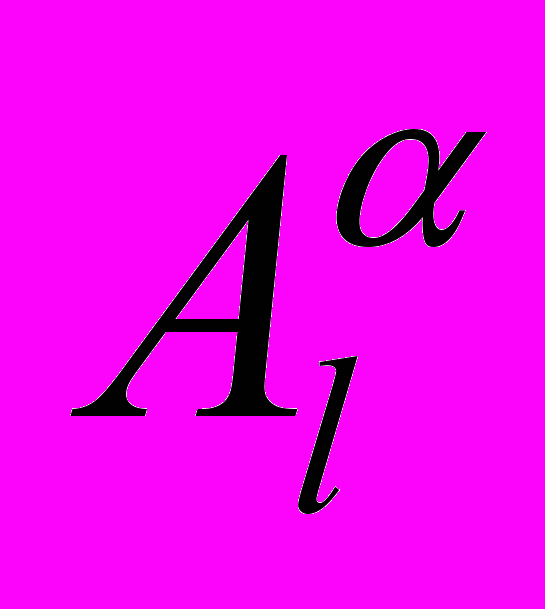 z +
z + 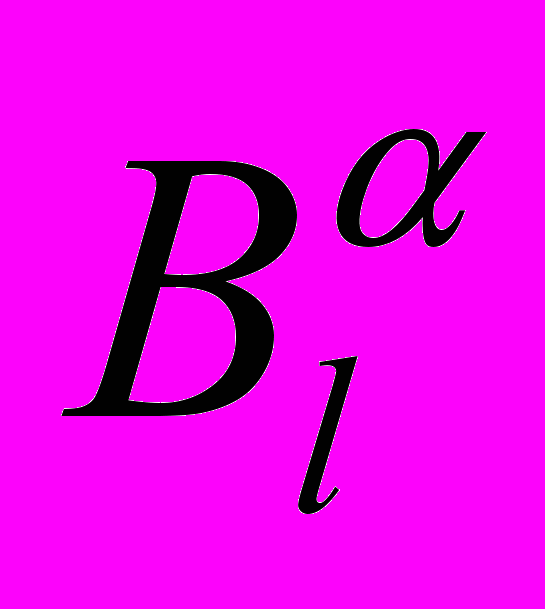 y, K
y, K Rn
Rn k. (9)
k. (9)Согласно (4) Al = Сl
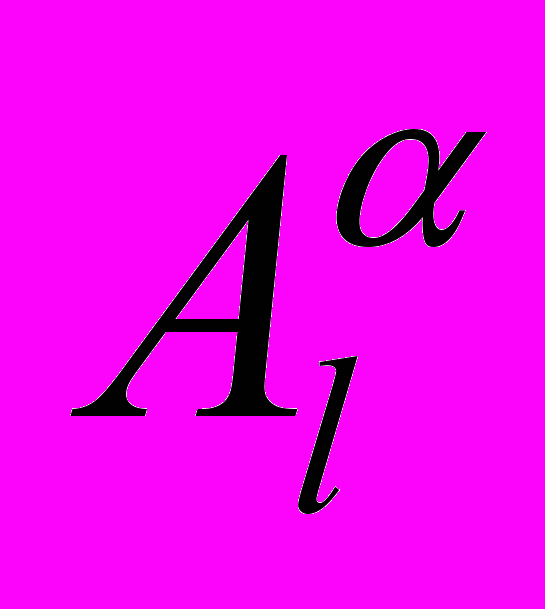 . Так как по условию матрица Al имеет полный ранг, то, согласно лемме из [5], матрица Сl также имеет полный ранг. Тогда в уравнении (8) K= 0n
. Так как по условию матрица Al имеет полный ранг, то, согласно лемме из [5], матрица Сl также имеет полный ранг. Тогда в уравнении (8) K= 0n k. Обозначая T=Wz-Vy и учитывая (9), запишем
k. Обозначая T=Wz-Vy и учитывая (9), запишем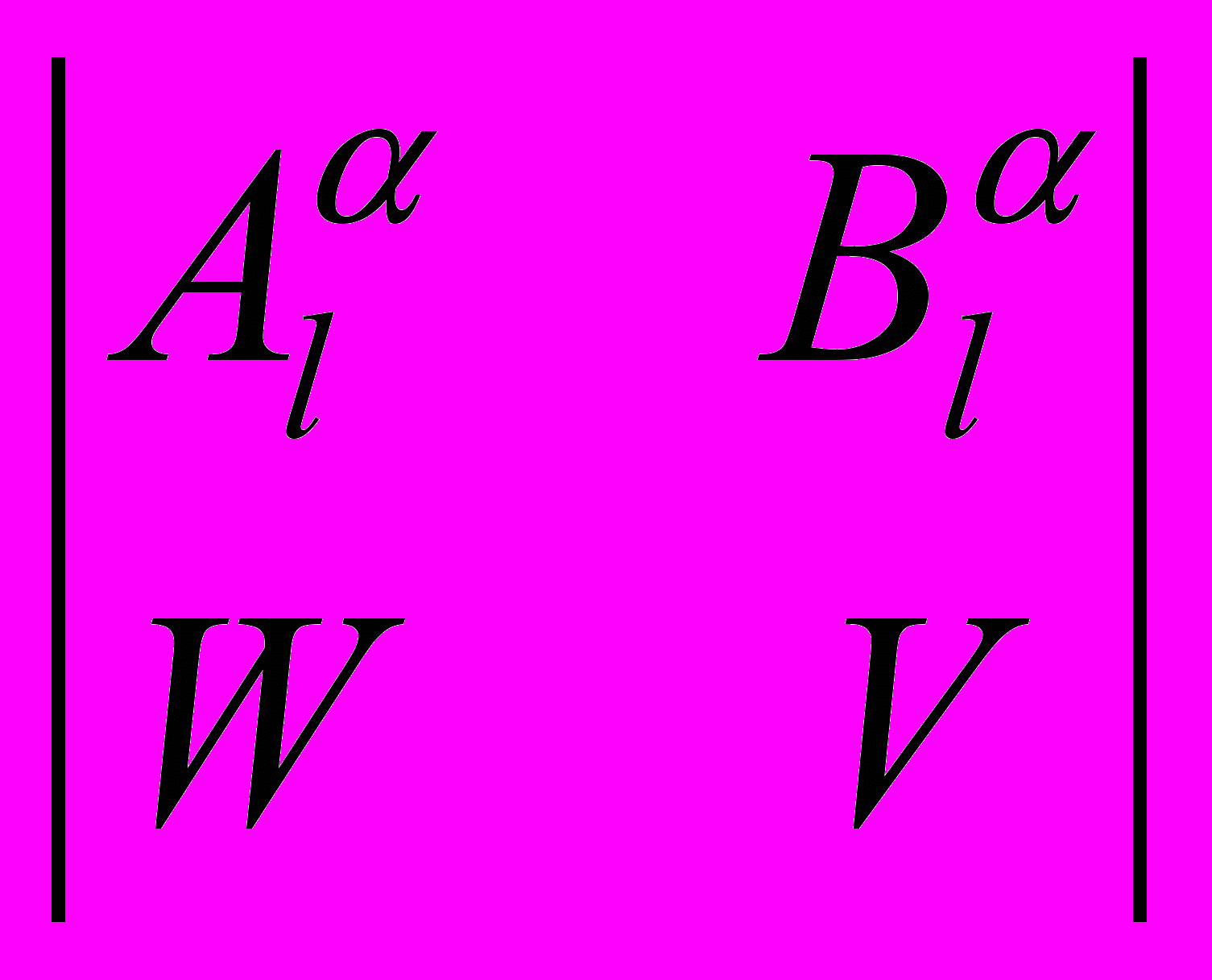
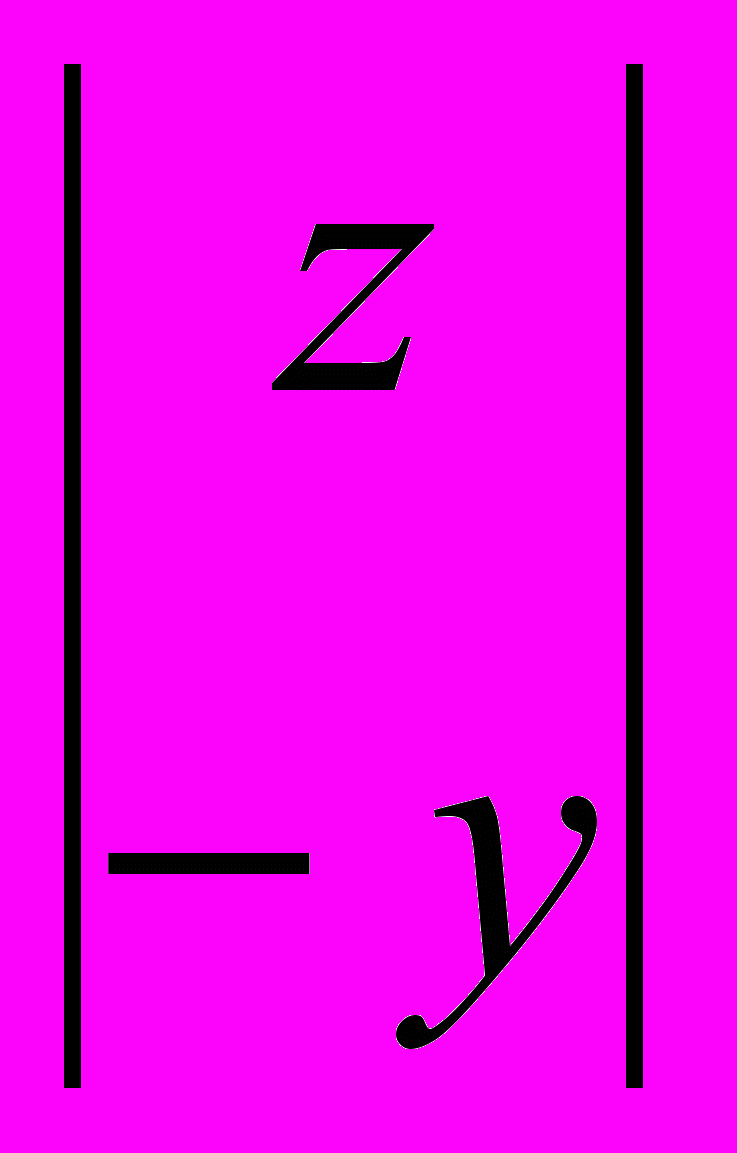 =
= , (10)
, (10)где W и V определены в (2). Умножим (10) слева на U. С учётом принятых в (2) и (3) обозначений, получим соотношение (7).
Предложение 2. Если в уравнении (5) матрица Al (Ar) имеет полный ранг, то и в соотношении (6) матрица
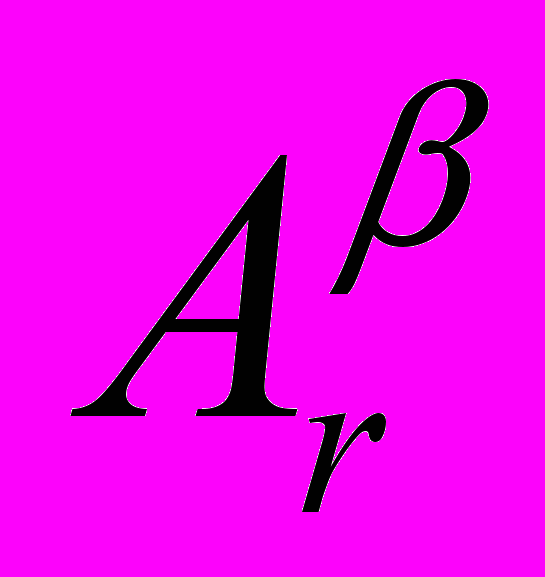 (
( ) имеет полный ранг.
) имеет полный ранг.Доказательство. В силу обозначений (2), (3) и соотношения U-1U=In+m, имеем
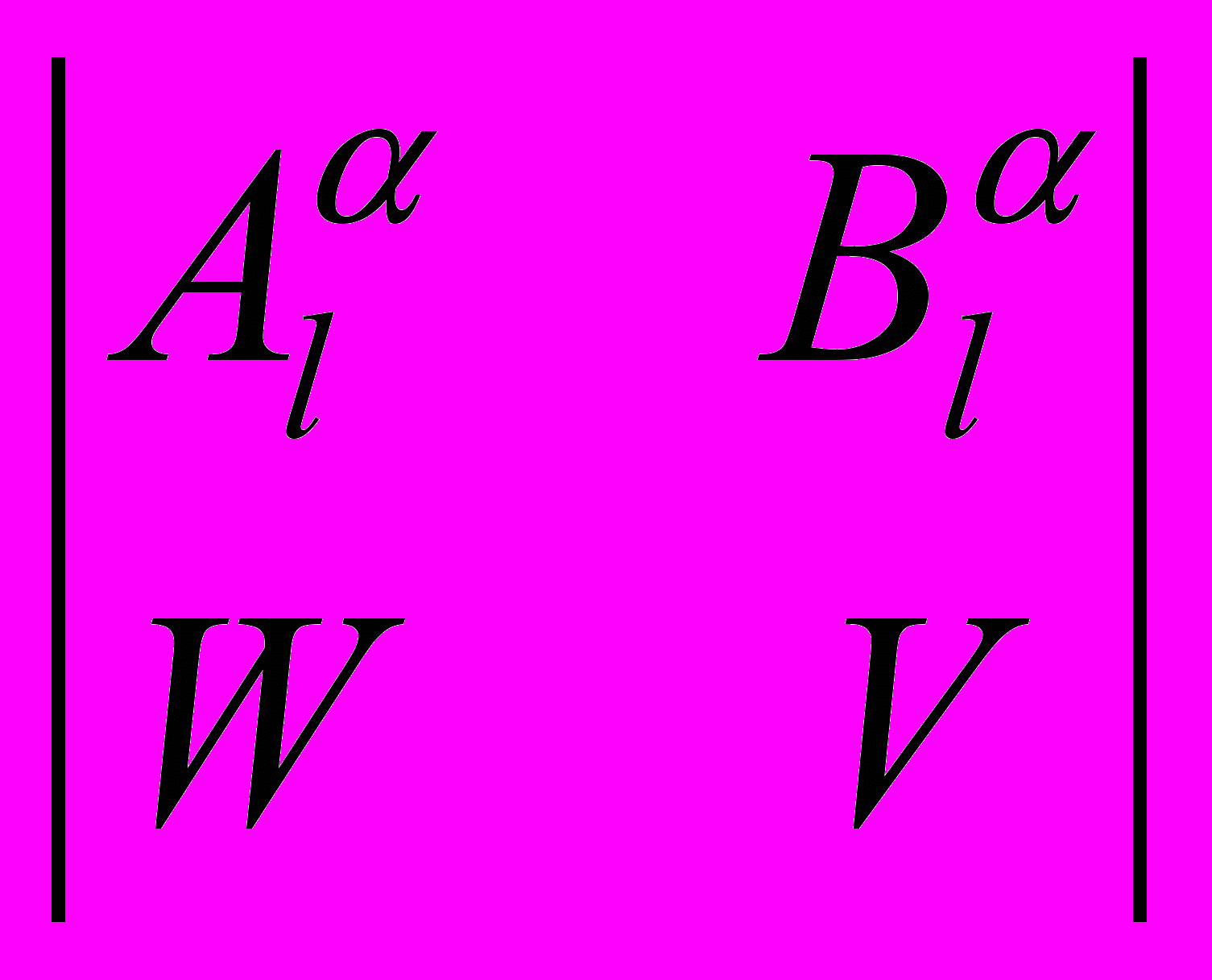
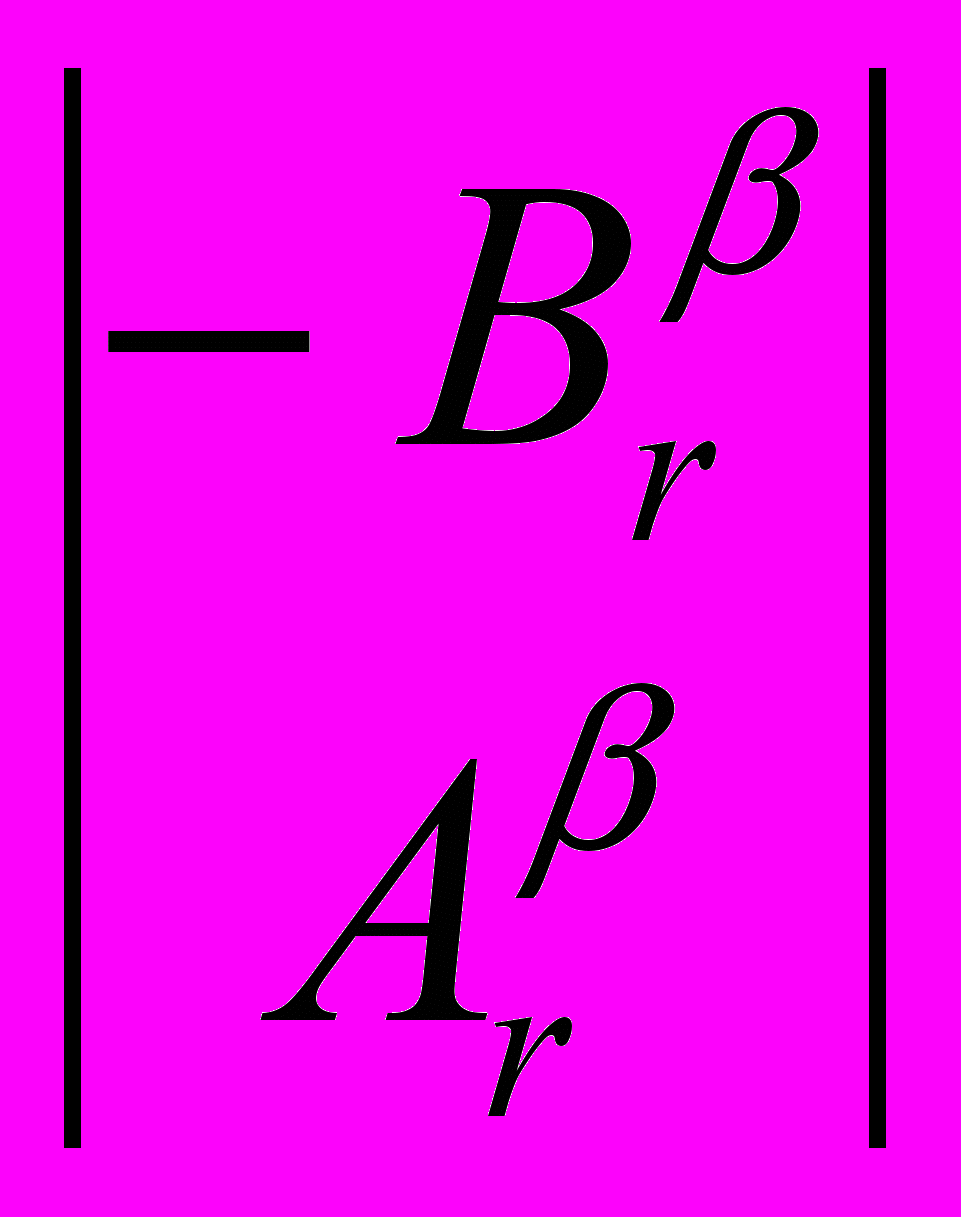 =
=  . (11)
. (11)Так как первый сомножитель в (11) обратим, ранг второго сомножителя равен m.
Rk
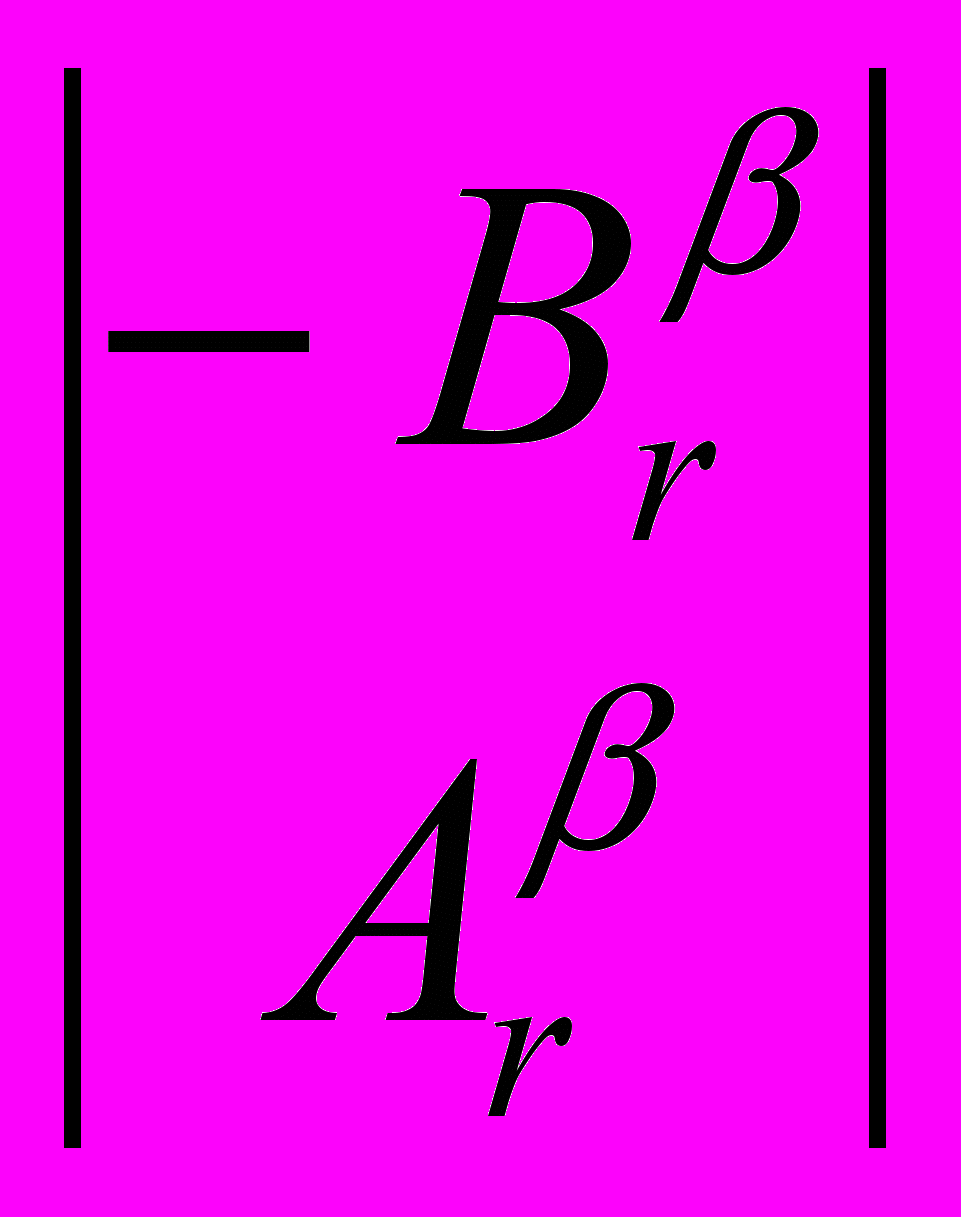 =m. (12)
=m. (12)Пусть матрица
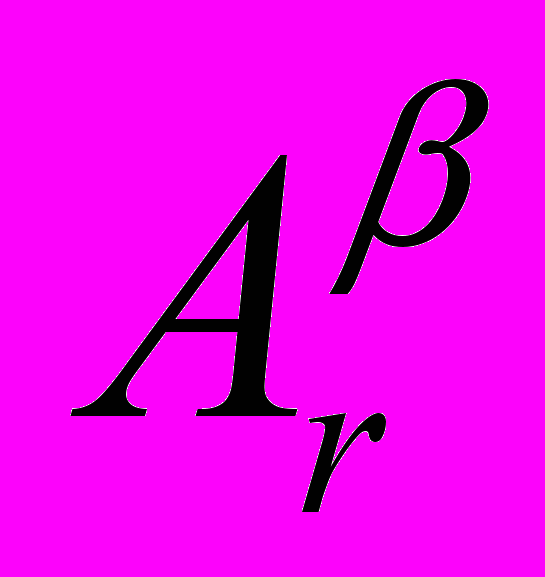 имеет неполный ранг. Тогда уравнение
имеет неполный ранг. Тогда уравнение 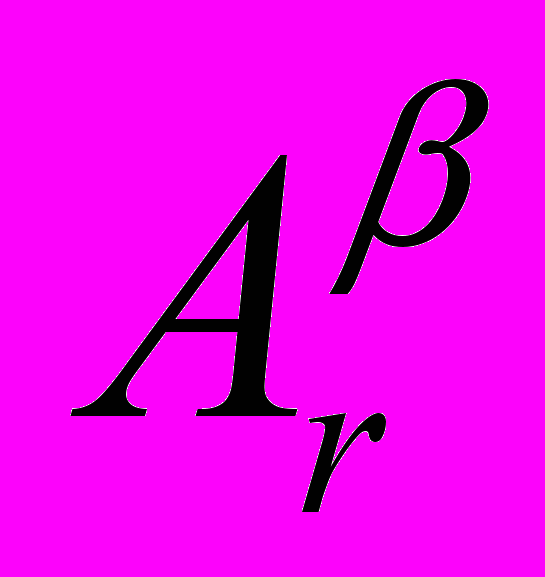 x=0m имеет нетривиальное решение x
x=0m имеет нетривиальное решение x Rm. Тогда
Rm. Тогда 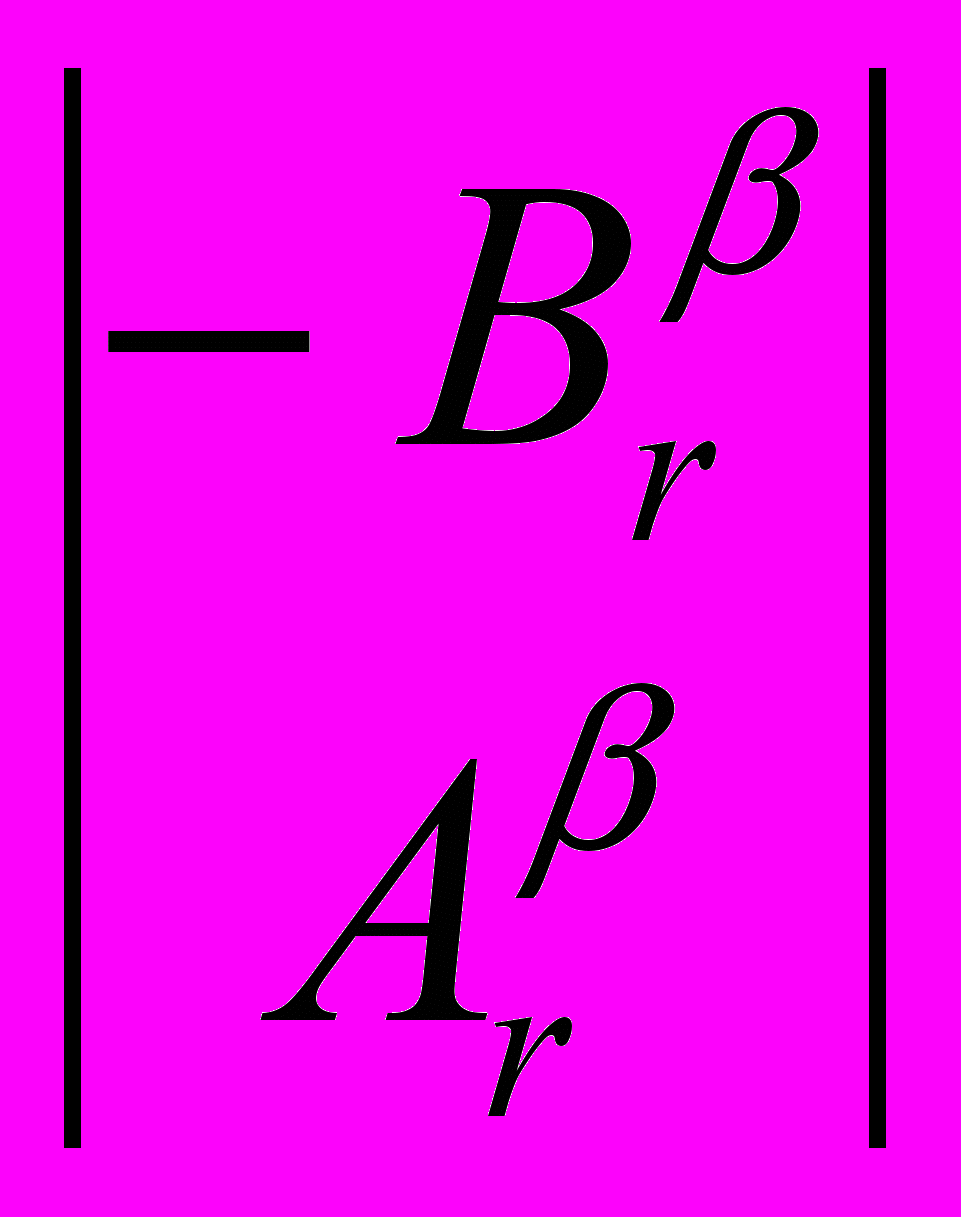 x =
x = 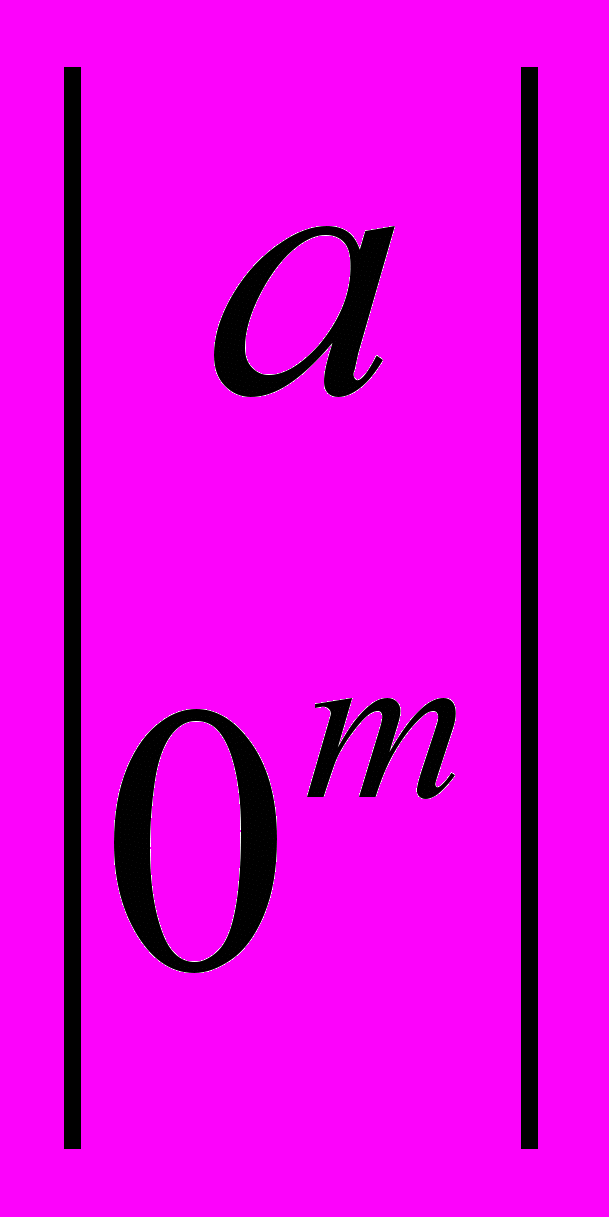 (13)
(13)для некоторого а
 Rn. В силу (12), имеем, что а не равно 0n. Умножая (13) слева на U-1 и учитывая обозначения (2) и (3) получим
Rn. В силу (12), имеем, что а не равно 0n. Умножая (13) слева на U-1 и учитывая обозначения (2) и (3) получим 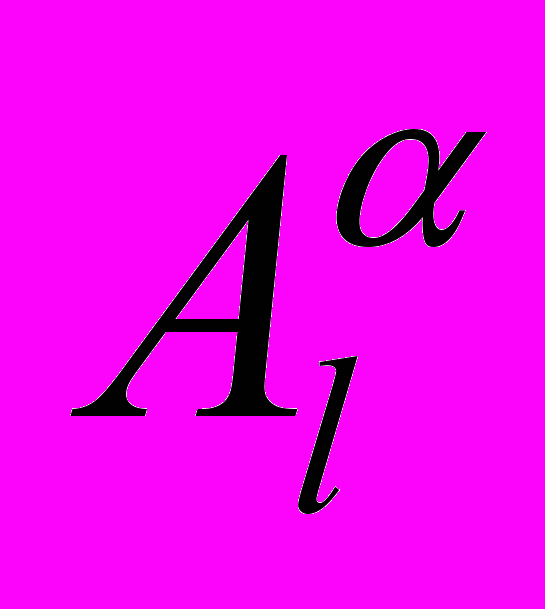 a=0n , что означает неполноту ранга матрицы
a=0n , что означает неполноту ранга матрицы 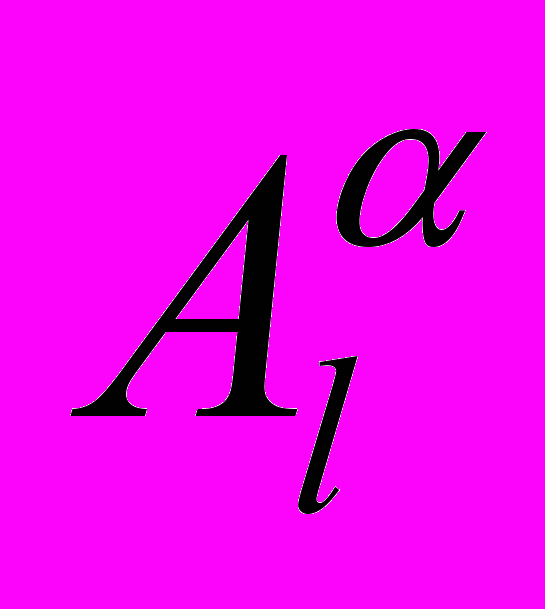 . Из соотношения (4) Al = Сl
. Из соотношения (4) Al = Сl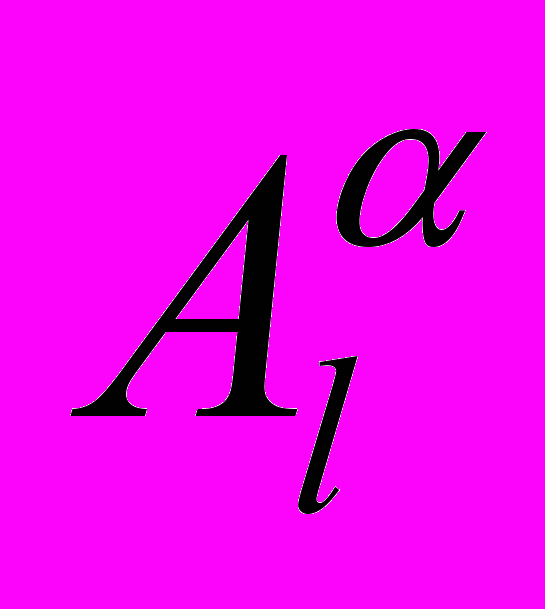 . По условию матрица Al имеет полный ранг. Согласно лемме из [5], матрица
. По условию матрица Al имеет полный ранг. Согласно лемме из [5], матрица 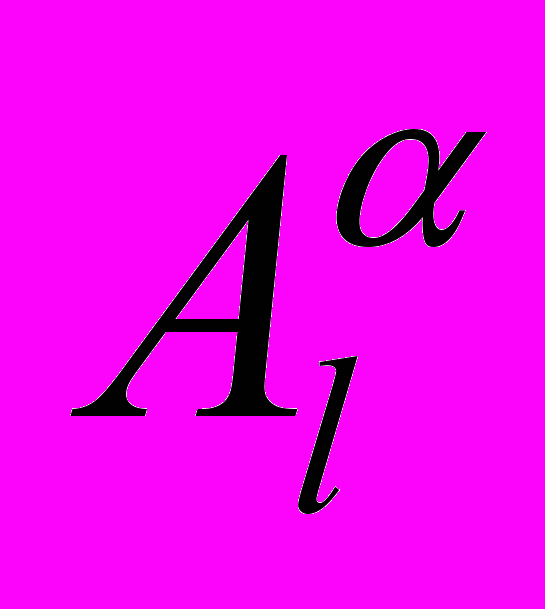 также имеет полный ранг. Противоречие.
также имеет полный ранг. Противоречие. Доказательство для матрицы Ar и
 проводится аналогично.
проводится аналогично.Предложение 3. ЛНОД (ПНОД) матриц Al и Bl (Ar и Br), где ранг rk Al равен n (rk Ar =m), определён с точностью до умножения справа (слева) на обратимую над R матрицу.
Доказательство. Пусть
AL =CiAi, BL=CiBi , (14)
где Ci
 Rnxn - ЛНОД матриц AL и BL, i=1,2. Согласно предложению 1, уравнение (5) имеет решение AL(-
Rnxn - ЛНОД матриц AL и BL, i=1,2. Согласно предложению 1, уравнение (5) имеет решение AL(-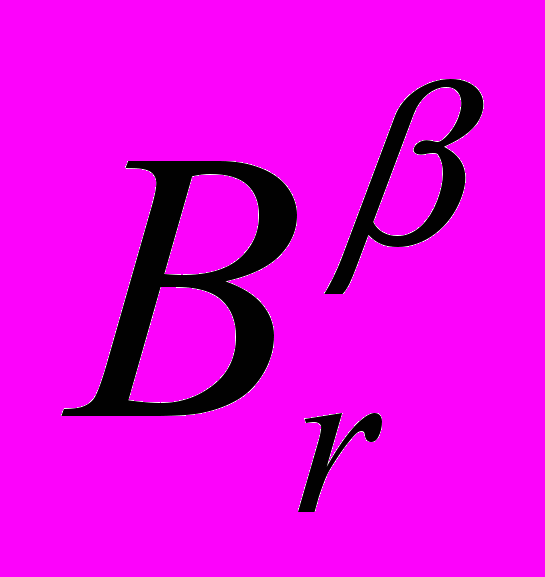 ) + BL
) + BL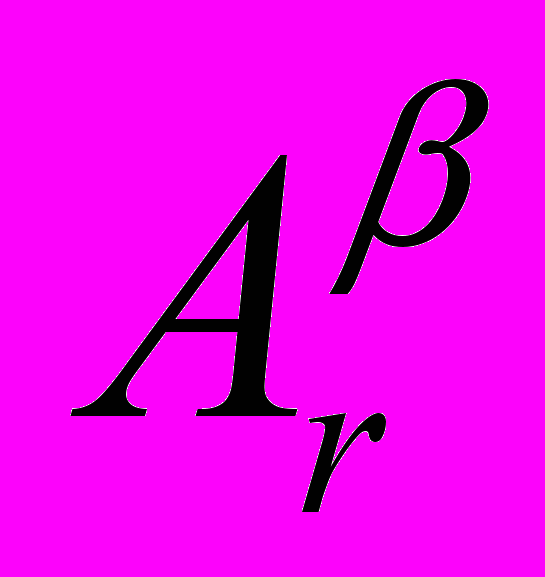 =0n
=0n m. Из предложения 2 следует, что rk
m. Из предложения 2 следует, что rk 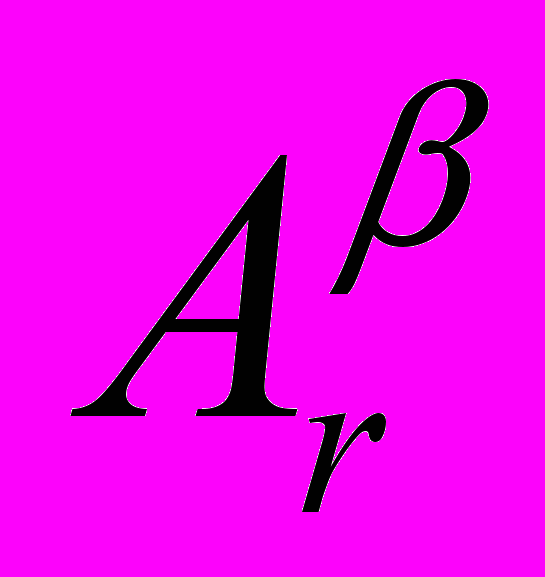 = m. Так как rk Al = n, то согласно лемме из [5], получим, что rk Ci= n и из (14) имеем
= m. Так как rk Al = n, то согласно лемме из [5], получим, что rk Ci= n и из (14) имеем Ai
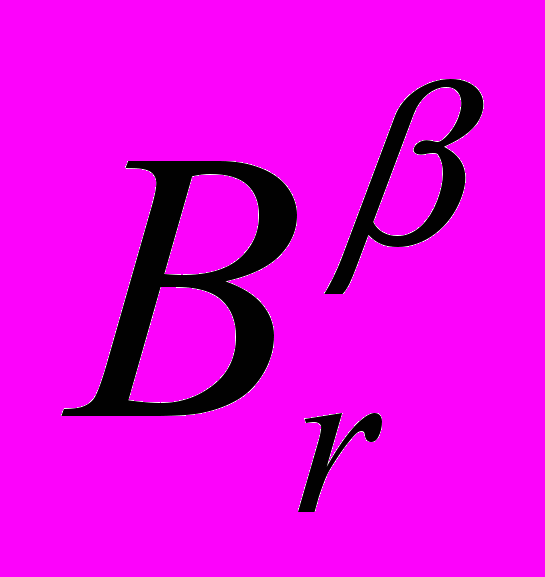 = Bi
= Bi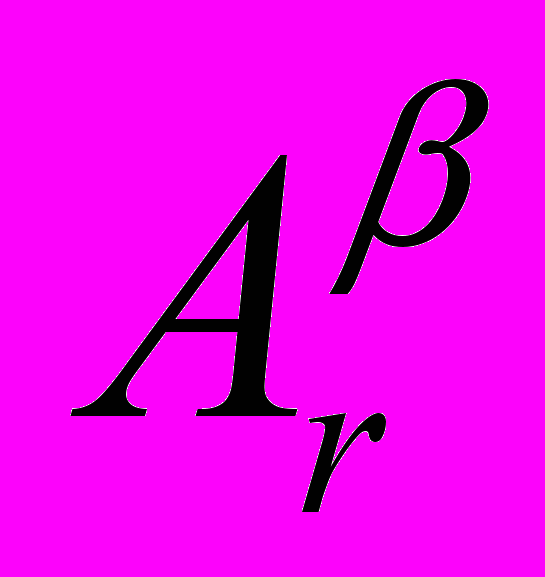 . 15)
. 15)Рассмотрим второе уравнение в (5), полагая Ar =
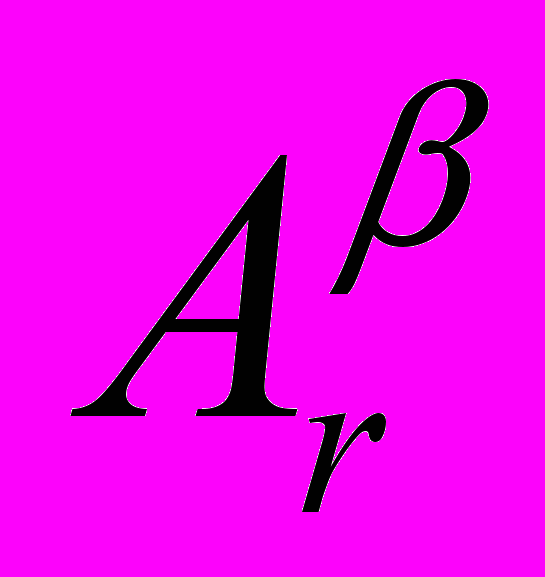 и Br =
и Br =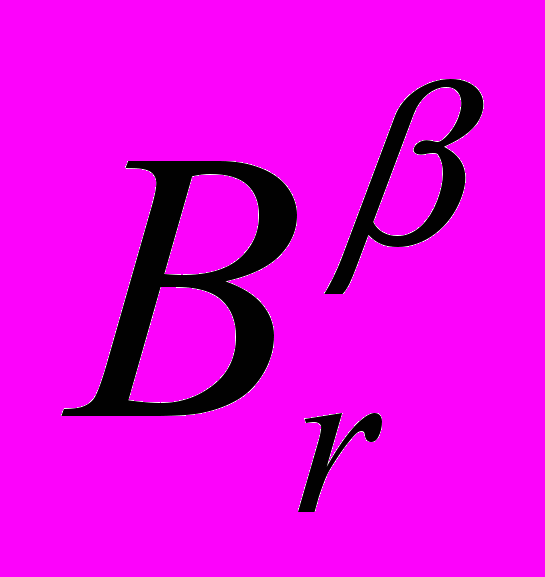 . Так как rk Ar = m, то согласно предложению 1, в (15) найдутся такие матрицы Ti, что Ai = Ti
. Так как rk Ar = m, то согласно предложению 1, в (15) найдутся такие матрицы Ti, что Ai = Ti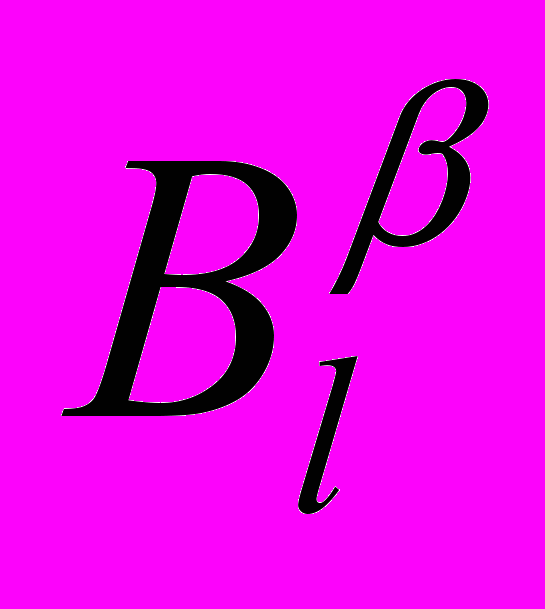 , Bi = Ti
, Bi = Ti , i=1,2. Поскольку матрицы Ai и Bi взаимно просты слева, то Ti-1
, i=1,2. Поскольку матрицы Ai и Bi взаимно просты слева, то Ti-1 Rnxn. Отсюда A2 = T2 T1-1 A1, B2 = T2 T1-1 B1 и тогда в (14) AL = C2T2 T1-1 A1= C1A1 и BL = C2T2 T1-1 B1= C1B1. Следовательно, C1= C2G, где матрица G= T2 T1-1лежит в Rnxn и обратима над R.
Rnxn. Отсюда A2 = T2 T1-1 A1, B2 = T2 T1-1 B1 и тогда в (14) AL = C2T2 T1-1 A1= C1A1 и BL = C2T2 T1-1 B1= C1B1. Следовательно, C1= C2G, где матрица G= T2 T1-1лежит в Rnxn и обратима над R.Доказательство для Ar и Br проводится аналогично.
Перейдём к матричным линейным неоднородным уравнениям.
Предложение 4. Уравнение ZA + YB =
 , где
, где  , A
, A Rm
Rm m, B
m, B Rn
Rn m, A = A1C, B = B1C, где С
m, A = A1C, B = B1C, где С Rm
Rm m – ПНОД матриц А и B, имеет хотя бы одно решение Z
m – ПНОД матриц А и B, имеет хотя бы одно решение Z Rm
Rm m, Y
m, Y Rm
Rm n, тогда и только тогда, когда C является правым делителем матрицы
n, тогда и только тогда, когда C является правым делителем матрицы  .
.Необходимость. Пусть уравнение имеет решение Z и Y. Тогда ZA1C + YB1C =
 1C =
1C =  , где
, где  1= A1C + YB1.
1= A1C + YB1.Достаточность. По условию матрицы A1 и B1 взаимно просты справа. Следуя предложению 1 из [6], имеем
Z0A1 + Y0B1 = Im, (16)
для некоторых Z0
 Rm
Rm m, Y0
m, Y0 Rm
Rm n. Если
n. Если  =
= 1C, то умножая (16) слева на
1C, то умножая (16) слева на  1 а справа на C получим частное решение исходного уравнения Z =
1 а справа на C получим частное решение исходного уравнения Z =  1Z0, Y =
1Z0, Y =  1Y0.
1Y0. Теорема. Предположим, что матрицы Ar
 Rm
Rm m, rk Ar =m и Br
m, rk Ar =m и Br Rn
Rn m, взаимно просты справа. Тогда уравнение
m, взаимно просты справа. Тогда уравнение ZAr + YBr =
 , (17)
, (17) при любой матрице

 Rm
Rm m имеет хотя бы одно такое решение Z
m имеет хотя бы одно такое решение Z Rm
Rm m, Y0
m, Y0 Rm
Rm n, что
n, что d(Y)
где матрица
 определена в (3) и d(.) - наивысшая степень дифференциальных операторов в матрице.
определена в (3) и d(.) - наивысшая степень дифференциальных операторов в матрице.Если матрицы Ar и
 собственные по столбцам [7] и наивысшие степени дифференциальных операторов в столбцах (cd(.)) матриц удовлетворяют соотношениям
собственные по столбцам [7] и наивысшие степени дифференциальных операторов в столбцах (cd(.)) матриц удовлетворяют соотношениямcdi(B r)
cdi(
 )=k+di, i=1,2…m, (20)
)=k+di, i=1,2…m, (20)где k= d(
 )-1, то все решения уравнения (17), удовлетворяющие неравенству (18), будут таковы, что матрица Z будет полного ранга и правильной по строкам. Причём
)-1, то все решения уравнения (17), удовлетворяющие неравенству (18), будут таковы, что матрица Z будет полного ранга и правильной по строкам. Причём rdi (Y)
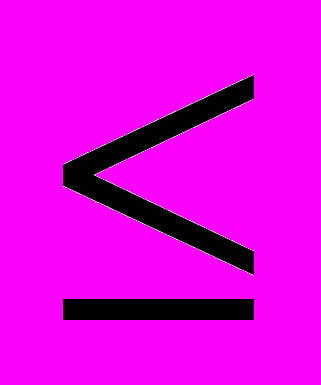 rdi (Z)=k, i=1,2…m, (21)
rdi (Z)=k, i=1,2…m, (21)где rdi (Y) - наивысшая степень дифференциальных операторов в i-й строке матрицы.
Доказательство. Так как A r и B r взаимно просты справа, то согласно [6], найдутся такие матрицы Z0
 Rm
Rm m, Y0
m, Y0 Rm
Rm n, что Z0A1 + Y0B1 = Im. Отсюда получаем частное решение уравнения (17). Согласно предложению 1, общее решение однородного уравнения ZAr + YBr = 0mxm равно Z = -T
n, что Z0A1 + Y0B1 = Im. Отсюда получаем частное решение уравнения (17). Согласно предложению 1, общее решение однородного уравнения ZAr + YBr = 0mxm равно Z = -T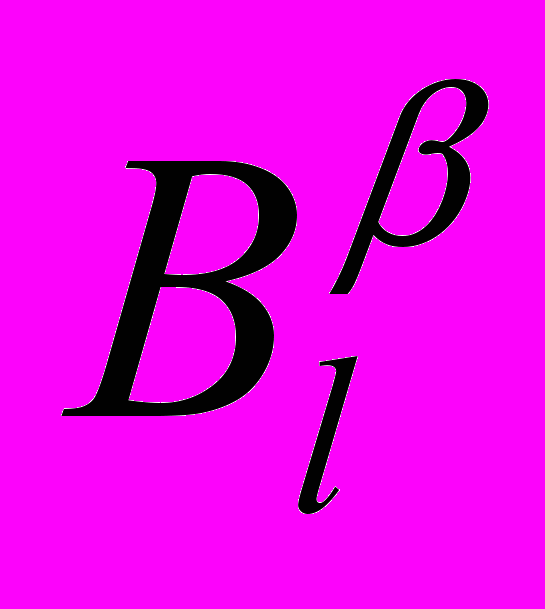 , Y = T
, Y = T  , где матрицы
, где матрицы  и
и 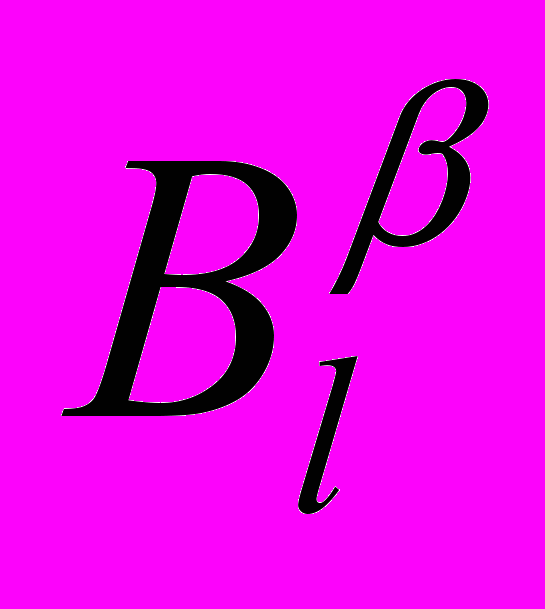 определены в (3) и T – произвольная матрица из Rn
определены в (3) и T – произвольная матрица из Rn n. Общее решение уравнения (17) примет вид
n. Общее решение уравнения (17) примет видZ=
 Z0 - T
Z0 - T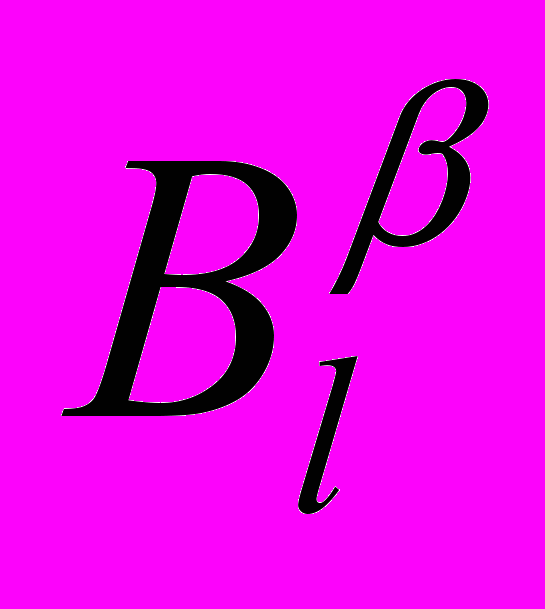 , Y=
, Y= Y0 + T
Y0 + T , (22)
, (22)Согласно предложению 2 rk
 =n. Согласно предложению 4 в [7], найдутся такие матрицы R, Q
=n. Согласно предложению 4 в [7], найдутся такие матрицы R, Q Rm
Rm n, что
n, что  Y0= Q
Y0= Q + R и степень d(R)
+ R и степень d(R)  Z0 +Q
Z0 +Q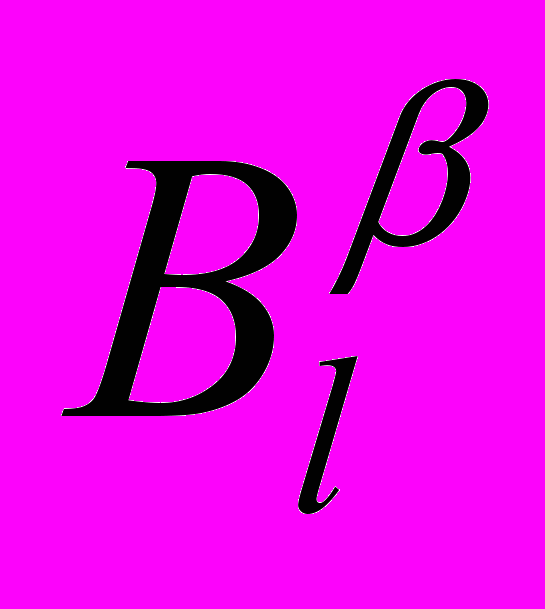 , которое удовлетворяет неравенству (18).
, которое удовлетворяет неравенству (18).Заметим, что степень решения может быть понижена, если, следуя предложению 1 из [7], сделать матрицу
 правильной по строкам.
правильной по строкам. Следуя [7], и учитывая обозначения (19) и (20), запишем Ar и
 в форме
в формеA r=CAdiag(pd1…pdm)+( A r)l, cd i (( A r)l)< d i,
 =CDdiag(pd1+k…pdm+k)+(
=CDdiag(pd1+k…pdm+k)+(  )l, cd i((
)l, cd i((  )l)< d i+k, i=1,2…m, (23)
)l)< d i+k, i=1,2…m, (23)где CA и CD – матрицы коэффициентов при наивысших степенях оператора дифференцирования p дифференциальных операторов в столбцах матриц A r и
 .
.Матрицу Z представим в виде
Z = prCZ + (Z) l, (24)
где CZ – матрица коэффициентов и d((Z) l)
 )l для некоторой матрицы D
)l для некоторой матрицы D Rm
Rm m. Причём cdi(D)< di+r, cdi(YBr)< di+k, i=1,2…m. Отсюда имеем r=k и CZCA=CD. По условию матрицы A r и
m. Причём cdi(D)< di+r, cdi(YBr)< di+k, i=1,2…m. Отсюда имеем r=k и CZCA=CD. По условию матрицы A r и  собственные по столбцам, что равносильно тому, что матрицы коэффициентов CA и CD имеют полный ранг [7]. Тогда и матрица CZ будет невырожденной. Следовательно, невырожденной будет и матрица Z. Таким образом, матрица Z в (24) будет правильной по строкам со степенями строк rd i(Z)=k, i=1,2…m, а поскольку имеет место неравенство (18), то справедливо и неравенство (21).
собственные по столбцам, что равносильно тому, что матрицы коэффициентов CA и CD имеют полный ранг [7]. Тогда и матрица CZ будет невырожденной. Следовательно, невырожденной будет и матрица Z. Таким образом, матрица Z в (24) будет правильной по строкам со степенями строк rd i(Z)=k, i=1,2…m, а поскольку имеет место неравенство (18), то справедливо и неравенство (21).Следствие. В скалярном случае (m=n=1) решение уравнения (17), удовлетворяющее условию (18) единственно. Причём при d(
 )=2d-1, где d=d(Ar), получаем d(Y)
)=2d-1, где d=d(Ar), получаем d(Y) 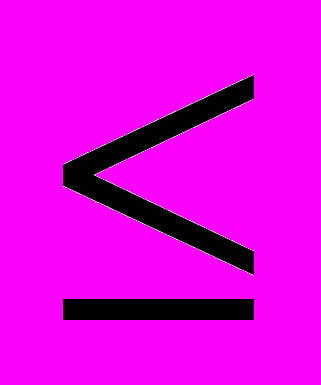 d(Z)=d-1.
d(Z)=d-1.Доказательство. Пусть существует два решения Y1, Y2
 R, удовлетворяющие (18). Согласно (22), имеем
R, удовлетворяющие (18). Согласно (22), имеем Y1 - Y2= T
 , (25)
, (25)для некоторого оператора T
 R. Из (5) и (6) следует, что
R. Из (5) и (6) следует, что 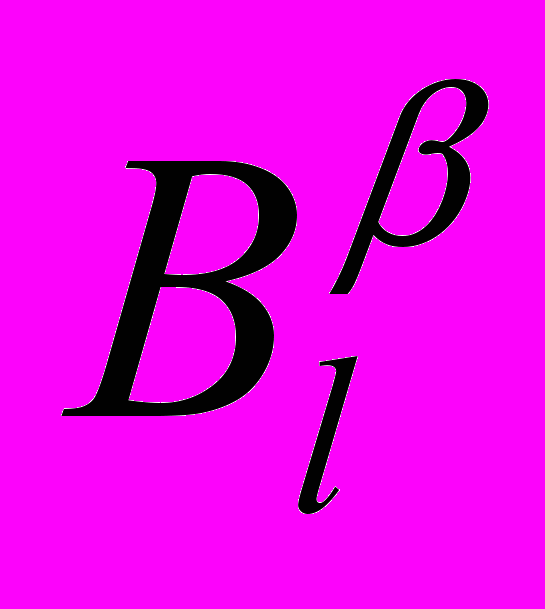 Ar =
Ar =  Br. По условию операторы Ar и Br взаимно просты справа. По построению операторы
Br. По условию операторы Ar и Br взаимно просты справа. По построению операторы 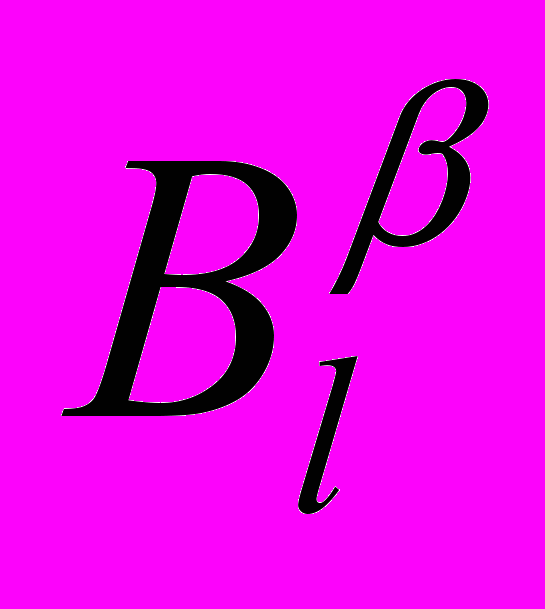 и
и  взаимно просты слева. Тогда
взаимно просты слева. Тогдаd = d(Ar) = d(
 ), d(Br) = d(
), d(Br) = d(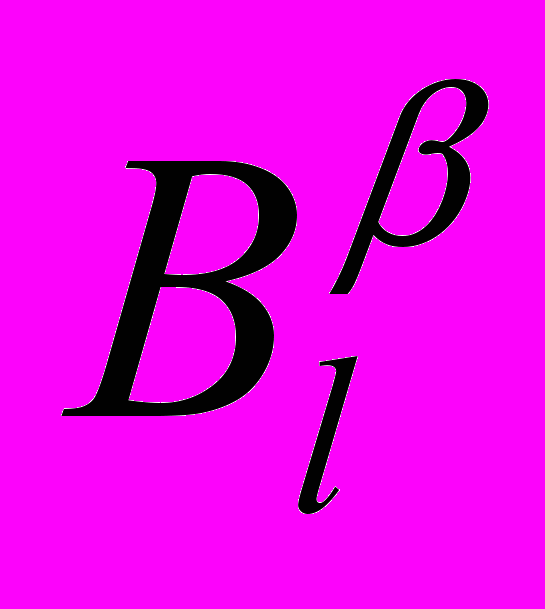 ). (26)
). (26)Так как, согласно (18) d(Y)
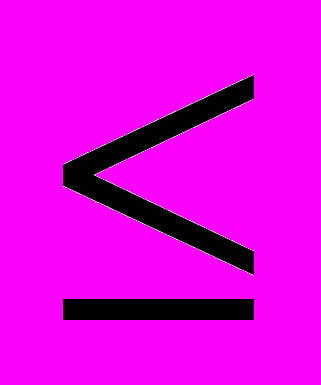 d-1, то в (25) имеем d(Y1 - Y2)
d-1, то в (25) имеем d(Y1 - Y2) 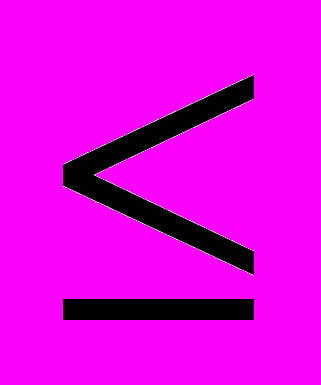 d-1 и d(T
d-1 и d(T )
)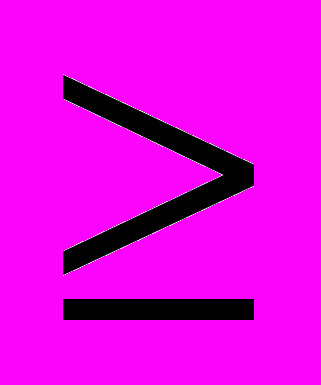 d. Противоречие, следовательно, Y1 = Y2. Перепишем уравнение (17) ZAr = - YBr +
d. Противоречие, следовательно, Y1 = Y2. Перепишем уравнение (17) ZAr = - YBr + . При заданных Ar и Br и полученном решении Y последнее уравнение имеет единственное решение Z.
. При заданных Ar и Br и полученном решении Y последнее уравнение имеет единственное решение Z. В скалярном случае условие (20) с учётом (26) примет вид d(
 )=2d-1. Тогда в (21) получим d(Y)
)=2d-1. Тогда в (21) получим d(Y) 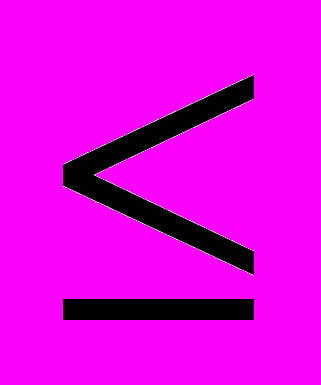 d(Z)=d-1.
d(Z)=d-1. Выводы. Получены конструктивные процедуры решения однородных и неоднородных линейных нестационарных дифференциальных матричных операторных уравнений, основанные на приведении матриц к треугольным формам, которое может осуществляться с помощью систем компьютерной алгебры Maple, Reduce, Singular, Gap и т.д.
ЛИТЕРАТУРА
1. Андреев Ю.Н. Алгебраические методы пространства состояний в теории управления линейными объектами. Обзор зарубежной литературы // Автоматика и телемеханика, 1977. № 3. с. 5-50.
2. Ylinen. An algebraic theory for analysis and synthesis of time-varying linear differentials systems // Acta Politechnica Scandinavica: Math. and Comput., Ser. N 32, Helsinki, 1980. 62 p.
3. Кон П. Свободные кольца и их связи. М.: Мир, 1974. 424 с.
4. Григорьев В.М. Формальные передаточные функции для линейных нестационарных систем // Системные технологии. Региональный межвузовский сборник научных трудов. - Выпуск 5 (28). - Днепропетровск, 2004. - с. 3–9.
5. Григорьев В.М. Ранги операторных матриц. // Системные технологии. Региональный межвузовский сборник научных трудов. - Выпуск 5 (28). - Днепропетровск, 2004. - с. 15–19.
6. Григорьев В.М. Совместность и эквивалентность линейных нестационарных систем управления // Системные технологии. Региональный межвузовский сборник научных трудов. - Выпуск 2 (10). - Дніпропетровськ, 2003. - с. 104–112.
7. Григорьев В.М. Правильные операторные матрицы // Системные технологии. Региональный межвузовский сборник научных трудов. - Выпуск 6 (41). - Днепропетровск, 2005. - с. 10–14.
Получено 14.10.09.
УДК 62-50:519.49
Григорьев В.М. Линейные нестационарные дифференциальные матричные операторные уравнения // Системные технологии. Региональный межвузовский сборник научных трудов. - Выпуск 5 (4). – Днепропетровск, 2009. - С.
Получены конструктивные процедуры решения однородных и неоднородных линейных нестационарных дифференциальных матричных операторных уравнений, основанные на приведении матриц к треугольным формам, которое может осуществляться с помощью систем компьютерной алгебры Maple, Reduce, Singular, Gap и т.д.
Библ. 7.
УДК 62-50:519.49
Григор’єв В.М. Лінійні нестаціонарні диференціальні матричні операторні рівняння // Системні технології. Регіональний міжвузівський збірник наукових праць. - Випуск 5 (64). - Дніпропетровськ, 2009. - С..
Отримані конструктивних процедури вирішення однорідних і неоднорідних лінійних нестаціонарних диференціальних матричних операторних рівнянь, засновані на приведення матриць до трикутної форми, яка може здійснюватися за допомогою систем комп'ютерної алгебри Maple, Reduce, Singular, Gap і т. і.
Бібл. 7.
УДК 62-50:519.49
Grigor’yev V. M. Linear time-dependent differential matrix operator equation // System technologies. N 5(64). – Dnepropoetrovsk. 2009. - P .
A constructive solution procedure for homogeneous and inhomogeneous linear nonstationary differential matrix operator equations based on the reduction of matrices to triangular forms, which may be implemented by computer algebra systems Maple, Reduce, Singular, Gap, etc.
Bibl.7
ISSN 1562- 9945
