«многочлены с одной переменной», рекомендованная для углубленного изучения математики в школе, является одной из немногих тем,относящихся к алгебре в том смысле, который вкладывается в это слово в математической науке. В отличие от большинства тем школьного курса алгебры, ориентированных в целом на
| Вид материала | Документы |
- Васюта Аленой Георгиевной. 2009 г. Набережные Челны решение, 41.28kb.
- «сведения, разъяснения, изложение», 44.82kb.
- Темы курсовых работ по дисциплине «Теория и методика обучения физике» Межпредметные, 19.14kb.
- Учитель математики и информатики моу сош №3 г. Ак-Довурака Саая, 282.99kb.
- Средняя школа города Мурманска №34, 582.67kb.
- Уроки в обучении математике, 111.17kb.
- Программа элективного курса для обучающихся 9 класса основной школы Тип элективного, 53.13kb.
- Одной из актуальных проблем современной методики преподавания русского языка является, 242.11kb.
- Етодика изучения темы «скорость химических реакций», 436.84kb.
- Рабочая программа курса «высшая математика (элементы аналитической геометрии и линейной, 67.54kb.
Тема «многочлены с одной переменной», рекомендованная для углубленного изучения математики в школе, является одной из немногих тем ,относящихся к алгебре в том смысле, который вкладывается в это слово в математической науке. В отличие от большинства тем школьного курса алгебры, ориентированных в целом на изучение функции, начала теории многочленов представляют собой математический аппарат для решения задач более широкого содержания, прежде всего решения уравнений и вопросов делимости целых и натуральных чисел.
Вопрос решения уравнения высших степеней был поднят Диофантом Александрийским (3 век нашей эры) – древнегреческим математиком. С начала Диофант исследовал системы уравнений второго порядка с двумя неизвестными; он указывал метод нахождения других решений если одно уже известно. Затем аналогичные методы он применял для решения высших степеней. С тех пор известны Диофантовы уравнения. Одну из дошедших до нас диофантовых линейных уравнений имеет вид
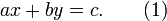. Затем к этой теме возвращаются только в 10 веке в странах ислама, после того как рукописи Диафанта были найдены и переведены на арабский язык. Методы Диофанта оказали огромное влияние на работы Пьера Ферма.Основное содержание этой темы тесно примыкает к темам «Квадратные уравнения» и «Квадратичная функция» общеобразовательного курса, алгебраический аспект которых ограничивается изучением квадратного трехчлена – в частности, уравнения третьей и более высоких степеней в курсе не рассматриваются.
Поэтому для меня важно изучить эту тему самостоятельно, для того чтобы решать уравнения высших степеней.
Цель моей работы изучить основы теории многочленов. Реализуя эту цель, я ставлю задачи:
- Изучить стандартный вид многочлена .
- Изучить основные методы нахождения корней многочлена.
- Изучить основные методы разложения на множители.
- Изучить основные методы решения уравнений.